土壤水分特征曲线Gardner模型参数预报研究
2019-09-10李浩然樊贵盛
李浩然 樊贵盛


摘要:为实现基于土壤基本理化参数的土壤水分特征曲线预测,以黄土高原地区农田土壤为研究对象,进行土壤水分特征曲线的系列试验,并配套测定了土壤基本理化参数,获取了G ardner模型参数与土壤基本理化参数间一一对应关系的数据样本。在分析研究各土壤理化参数与G ardner模型参数间单因素关系的基础上,创建了以土壤黏粒含量、粉粒含量、干密度、有机质含量为输入变量的水分特征曲线G ardner模型参数多元非线性预报模型。结果表明:以土壤黏粒含量、粉粒含量、干密度、有机质含量为输入因子,对G ardner模型参数进行预测是可行的,建模样本的拟合相对误差平均值小于11%,用检验样本进行预测的相对误差平均值小于10%,预测精度较高。
关键词:土壤水分特征曲线;非线性模型;Gardner模型;参数预测;样本检验
中图分类号:S152; TV93
文獻标志码:A
doi:10.3969/j.issn.1000- 1379.2019. 04.033
土壤水分特征曲线是土壤水基质势或土壤水吸力随土壤含水率变化而变化的关系曲线,反映了土壤水的能量与数量之间的关系,是研究土壤水分的保持和运动所用到的反映土壤水分基本特性的曲线[1]。
目前,常用的土壤水分特征曲线模型的获取方法分为直接法与间接法。直接法即传统的负压计法、压力膜仪法、砂性漏斗法,这些方法能够在实验室中利用相关的仪器,较准确地测得相应的土壤水分特征曲线,但成本较高、操作繁琐、耗时较长而且试验结果存在不确定性。随着土壤传输理论的发展和计算机科学的进步,以建立土壤传输函数[2]为核心获取土壤水分特征曲线的间接法成为研究热点。土壤传输函数是以易获取的土壤基本理化参数(如土壤质地、密度等)为输入变量,通过某种算法,建立土壤基本理化参数与水分特征曲线模型参数之间的函数关系,从而实现对土壤水分特征曲线的预测。国内外学者针对土壤传输函数的研究甚多,Vereecken等[3]运用线性函数对土壤水分特征曲线进行了研究,对模型参数进行了线性函数预测:韩勇鸿等[4]利用土壤传输函数,针对田间持水率建立神经网络预报模型,并建立了准确的预报模型;李晓鹏等[5]使用多种不同的土壤传输函数,对不同地区土壤的饱和导水率进行了预测,并得出适合不同地区的土壤饱和导水率。
当前,在众多土壤水分特征曲线经验或物理一经验模型中,Gardner模型因形式简单、参数少、预测精度高而广泛应用。宋孝玉等[6]通过不同区域土壤Gardner模型的建立与比较,证明了Gardner模型的准确性与适用性。肖恩邦等[7]使用Gardner模型进行拟合,对陕北地区的土壤水分特征曲线与土壤水势特征进行了研究:杜红普等[8]结合Gardner模型对多孔介质毛细水上升进行预测,获得了多孔介质毛细水上升的具体过程:伍海兵等[9]采用Gardner模型对上海市土壤进行了植被类型与土壤物理性质的分析和研究,得出不同植被类型的土壤供水能力。
但是,纵观国内外研究成果,综合考虑土壤质地、结构以及有机质含量对土壤水分特征曲线模型参数影响的研究鲜有报道。本研究以黄土高原地区土壤水分特征曲线试验为依据,在分析土壤黏粒含量、粉粒含量、干密度以及有机质含量对Gardner模型参数影响的基础上,建立基于土壤理化参数的Gardner模型参数非线性预报模型,以实现对土壤水分特征曲线模型参数的预测,为黄土高原地区土壤水分研究提供技术支撑。
1 材料与方法
1.1 土壤条件
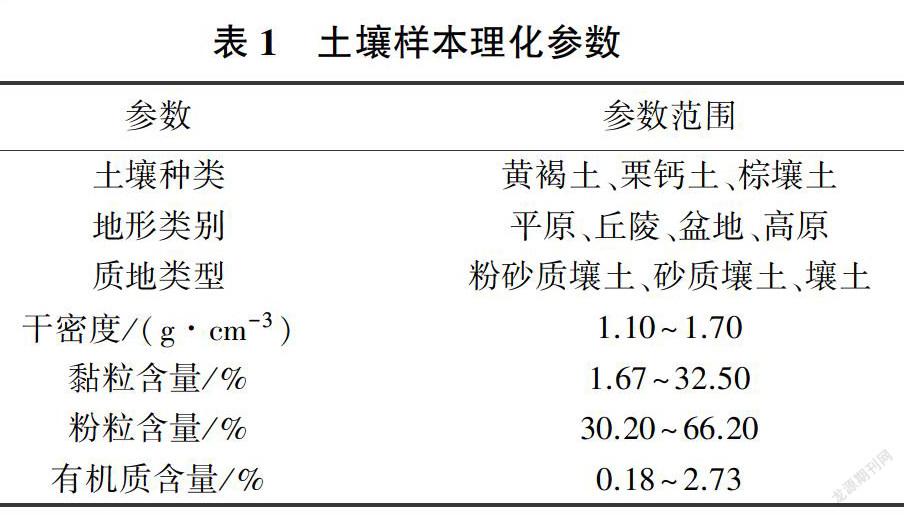
本试验所用的土壤全部取自区山西省中西部地区农耕田。试验区属于典型的温带大陆性气候区,春秋季干燥多风,夏季炎热潮湿,冬季寒冷干燥,全年降水主要集中在7-8月。试验所用土壤的各理化参数见表1。
1.2 试验方案
1.2.1 试验设计
根据土壤基本理化参数对土壤水分特征曲线模型参数的影响,对不同土壤条件下土壤质地、土壤干密度、土壤有机质含量进行测定,从而获得土壤水分特征曲线Gardner模型参数。具体试验的设计如下。
土壤水分特征曲线:土壤水分特征曲线利用压力膜仪进行测定,并利用Gardner模型对实测数据进行拟合,进而得到模型参数。
土壤质地:对试验区深度为0 - 20、20 -40 cm的土壤黏粒含量、粉粒含量、砂粒含量进行试验测定。
土壤密度:由于本次试验的土样样本为扰动土,因此需要配置不同的密度值。为了让密度水平基本涵盖黄土高原土壤密度变化范围,设计10个密度值,分别为1.00、1.10、1.20、1.30、1.350、1.40、1.450、1.50、1.60、1.70 g/cm。
土壤有机质含量:测定0~20、20 -40 cm土层土壤的有机碳含量,经过换算得到有机质含量。
1.2.2 试验方法
(1)水分特征曲线模型参数试验。土壤水分特征曲线采用美国产1500F型压力膜仪进行测定。首先,装备试验土样并使其自然风干,将土样过1 mm筛后均匀装在体积为20 cm3、高度为1 cm的环刀中,环刀需垫滤纸,土样的上界面与环刀顶缘齐平。其次,使土样水分饱和,将整理好的环刀放人压力膜仪中的陶土板上,并在陶土板下加入适量水,以保证土样吸水达到水分饱和,24 h后进行土样饱和含水率测定。然后,对土样进行加压,按设置的压力值逐级加压,如0.3、0.6、1.0、3.0 bar等,最大为15.0 bar,在加压过程中,土样受到压力作用排出的水分经过排水系统排出。在设定压力下,每隔相同时间(如24 h)对土样进行质量测定,如果前后两次的质量差异小于0.005 9,则认为土样在设定压力下不能保持的水分全部排出,可以进行下一个压力等级的试验。最后,在所有压力值的测定完成后,计算出不同压力值下土样的体积含水率,从而得到不同水吸力下的土壤含水率,通过拟合,得到相应的模型参数。
(2)其他土壤理化参数试验。本研究建模所涉及的土壤理化参数主要有土壤质地、土壤密度、土壤有机质含量。采用激光粒度分析仪进行黏粒、粉粒、砂粒含量的测定;在压力试验结束后对土样烘干称重,测得其密度值;土壤有机质含量的则采用重铬酸钾容量法。
1.3 模型简介
目前关于土壤水分特征曲线的经验模型有VG模型、Gardner模型、F-X模型等。Gardner模型是Gardner等10-11]在1970年正式提出的,该模型结构简单,计算方便,精度较高并且适用性强。Gardner模型的具体表达式为
h= aθ(1)式中:h为土壤水吸力(用水头表示),cm;θ为土壤体积含水率,%;a、b均为拟合参数,无量纲且均大于0。
2 土壤传输函数的建立
2.1 输入因子与输出因子的确定
土壤理化条件的变化会引起土壤水分特征曲线Gardner经验模型参数的变化,本研究采用土壤传输函数的方法,建立土壤水分特征曲线Gardner经验模型参数与土壤基本理化参数间的非线性关系模型,从而解决土壤水分特征曲线模型参数变化大、获取困难的问题。对于选定的土壤水分特征曲线模型,所建非线性预测模型的输出因子为Gardner模型的参数a和b。
根据关于土壤水分特征曲线的研究可知,影响土壤持水能力的因素非常多,土壤的质地、土壤干密度、土壤有机质含量等均是重要的影响因子,这些因素会通过影响土壤的持水能力来影响Gardner模型参数的大小。土壤中如果黏粒与粉粒含量较高,则会在土壤中形成较多的中小孔隙,中小孔隙的增加首先会增大土壤中的毛管吸力,土壤的持水能力因此变强,同时中小孔隙的增加能够增大土壤的比表面积,使得土壤颗粒对土壤中水分的吸附能力变强:对于多孔隙土壤而言,土壤密度的增大意味着土体被压缩,土壤中的大孔隙会受到挤压破坏,大孔隙经过压缩后成为中小孔隙,同时中小孔隙的增加又会增大土壤的毛管吸力和土颗粒的表面吸附能力:土壤中的有机质主要指土壤内无机碳的胶结物,这些物质会增加土壤的黏性和改变土壤的内部结构,有机质含量高的土壤会在胶结物的影响下形成大量稳定性较强的中小孔隙,增加土壤的毛管吸力,从而使得土壤的持水能力增强。
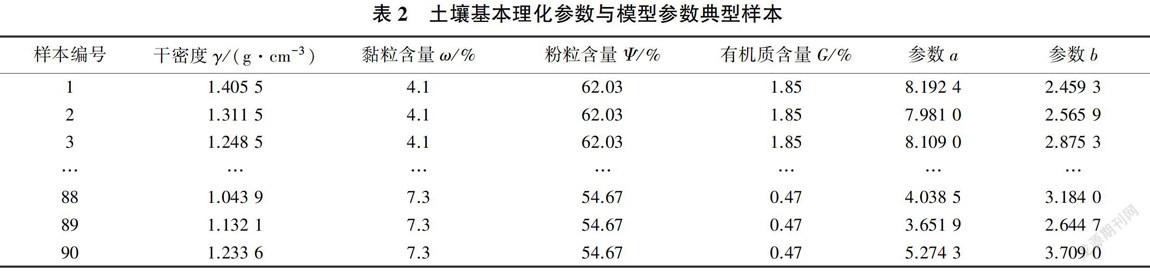
综上所述,最终选取土壤黏粒含量、粉粒含量、干密度与有机质含量为输入因子,以Gardner模型参数a与6为输出因子,建立非线性关系模型。本研究通过大量的试算与拟合,去掉奇异值后将90组数据作为建模样本,并且随机预留8组数据作为检验样本。建模样本见表2。
2.2 单因素函数结构的确定
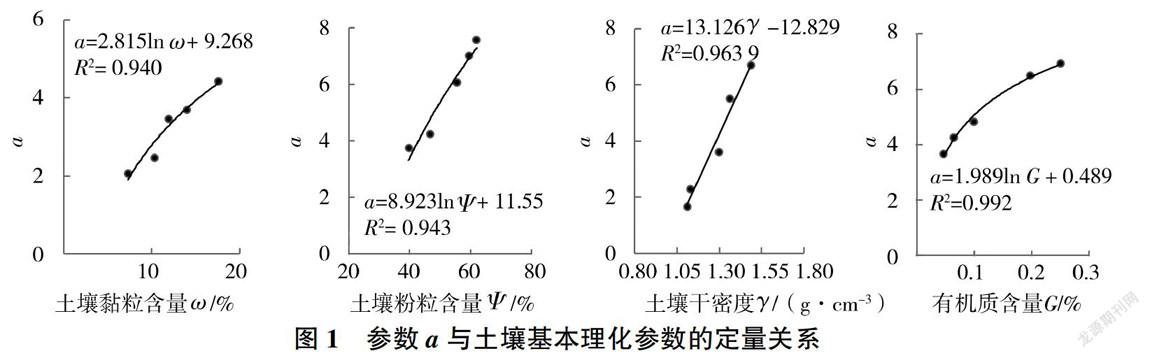
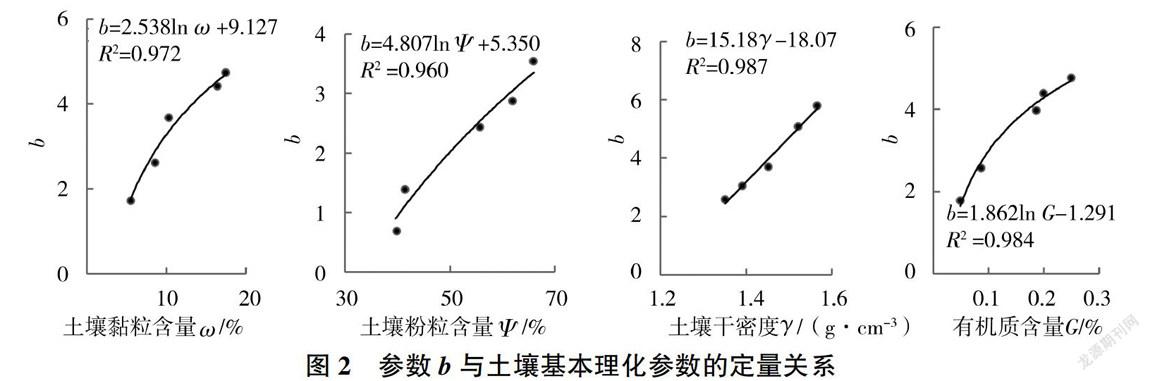
为了验证不同土壤基本理化参数与Gardner模型参数之间的函数关系,对输入变量进行单因素分析。通过控制变量的方法,在其他因素相同时,每种土壤基本理化参数选取5组样本数据进行分析与拟合(见图1、图2),从而确定单因素的最佳函数结构。
如图1、图2所示,土壤黏粒含量ω与Gardner模型参数a和b成对数关系:土壤粉粒含量ψ与Gardner模型参数a和b成对数关系;土壤干密度γ与Gardner模型参数a和b成线性关系:土壤有机质含量G与Gardner模型参数a和b成对数关系。
2.3 多元非线性函数结构形式的确定
(1)非线性函数结构形式的初步确定。将各单因素的拟合方程进行简单的机械叠加,并将各常数项合并,得到非线性函数结构的初步形式:
(2)输入因子的显著性检验。对于输入因子的显著性检验又称T检验,需要将建模样本输入已经编写好的程序,通过运行程序得到T检验的结果与方程的系数。将得到的T检验结果与T0.025=2.014 4进行比饺,如果|T|
由表3可知,黏粒含量、粉粒含量、土壤干密度及有机质含量的T检验结果均大于T0.025,证明选取的输入因子是合理的,可以用来对Gardner模型参数进行多元非线性预测。
(3)函数方程的显著性检验。对于函数方程的显著性检验又称F检验。除了对输入因子的显著性检验外,还需对整个方程进行显著性检验。给定显著水平a=0.05.通过查找资料得到F0.05= 3.1。通过程序计算得到的F值如果大于F0.05则显著,反之不显著。检验结果见表4。
由表4可知,参数a与b的F值均大于F0.05,因此参数a与b的函数方程显著,可信度较高:同时得出训练样本对于参数a与b预测结果的平均相对误差分别为10.07%与10.51%.误差在11%以内,预测精度较高。
(4)根据Madab程序拟合计算,最终得出Gardner模型参数的非线性回归方程的系数,并确定参数a与b的多元非线性预测模型如下:
3 样本检验与误差分析
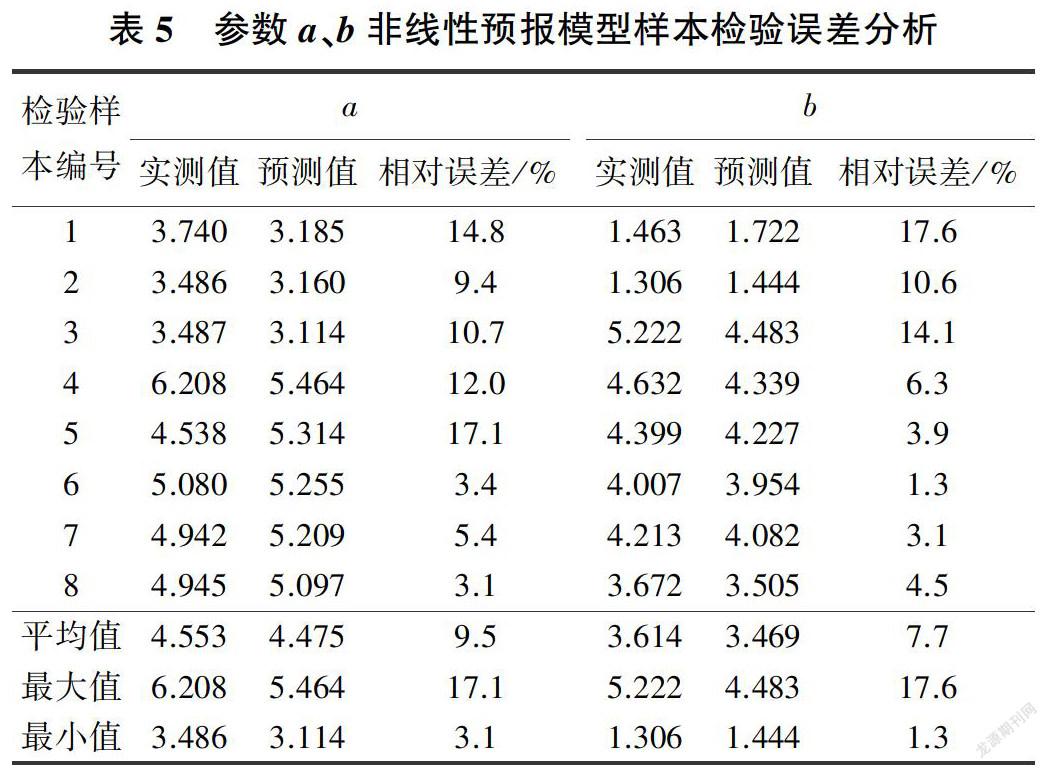
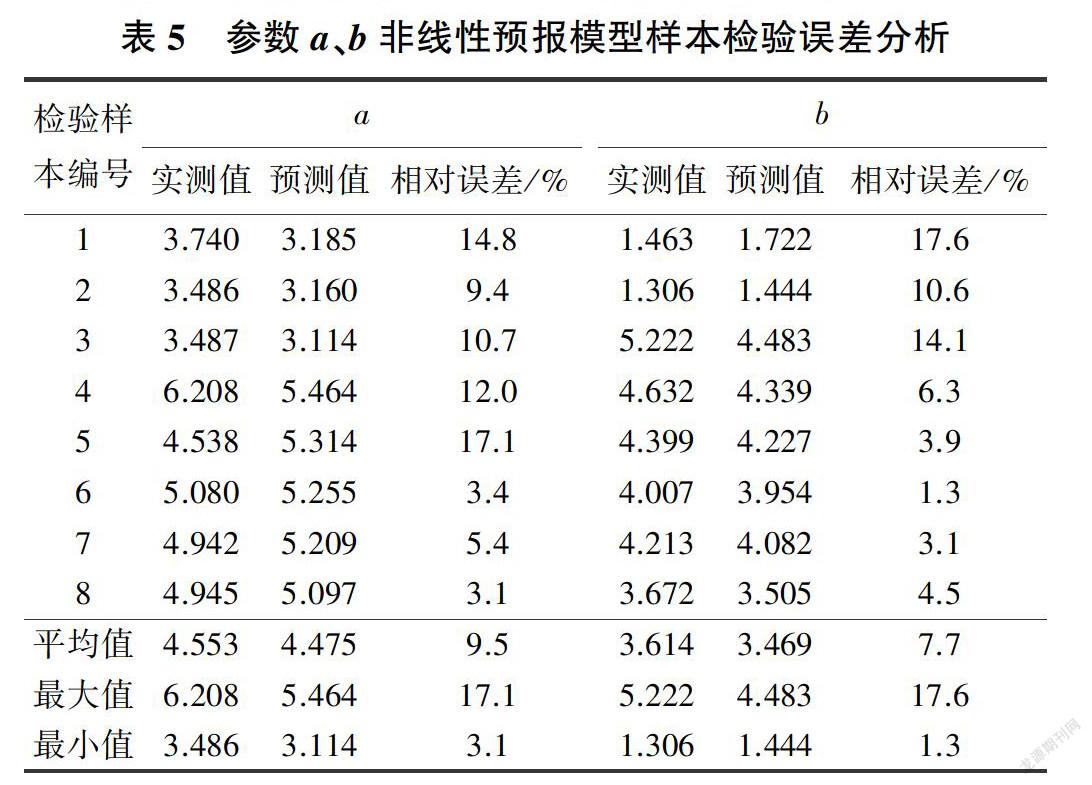
使用预留的8组数据对参数a与b的多元非线性预报模型进行检验,样本检验误差分析见表5。
分析表5中的数据,可以发现本研究建立的关于Gardner模型参数的多元非线性预报模型对于参数a的预测相对误差的最大值为17.1%,最小值为3.1%,相对误差的平均值为9.5%:对于参数6的预测相对误差的最大值为17.6%,最小值为1.3%,相對误差的平均值为7.7%。误差分析结果表明,基于90组样本数据建立的多元非线性预报模型对土壤水分特征曲线Gardner模型参数的预测平均相对误差小于10%,预测精度在可接受的范围之内。
4 结论
(1)运用土壤传输函数法对土壤水分特征曲线Gardner模型参数进行多元非线性预报模型的预测是可行的,Gardner模型参数的预测误差在可接受的范围之内,此预测模型可以应用于黄土高原田间土壤持水能力研究中。
(2)把土壤黏粒含量、粉粒含量、干密度、有机质含量作为预测土壤特性曲线Gardner模型参数预报模型的输入变量是可行的,试验结果为简便、准确获得Gardner模型参数以及土壤水分特征曲线提供了理论上的支撑。
本研究只对Gardner模型参数进行了预测,以后的研究中可对不同模型的参数进行预测与比较,从而验证非线性模型的准确性及适用性。同时,应尝试主成分分析、灰色关联理论等不同的改进算法来进一步优化预测模型。
参考文献:
[1]雷志栋,杨诗秀,谢传森,土壤水动力学[M].北京:清华大学出版社,1988:17-22.
[2] 朱安宁,张佳宝,陈效民,等,封丘地区土壤传递函数的研究[J].土壤学报,2003,40(1):53-58.
[3]VEREECKEN H J,MAES J,FEYEN J,et al.Estimating theSoil Moisture Retention Characteristic From Texture, BulkDensity and Carbon Content[J].Soil Science, 1989, 148(6):389-403.
[4] 韩勇鸿,樊贵盛,孔令超,田间持水率土壤传输函数研究[J].农业机械学报,2013,44(9):62-67.
[5] 李晓鹏,张佳宝,吉丽青,等,土壤传递函数在计算土壤饱和导水率中的应用[J].灌溉排水学报,2009,28(2):70-73.
[6]宋孝玉,李亚娟,李怀有,等,土壤水分特征曲线单一参数模型的建立及应用[J].农业工程学报,2008,24(12): 12-15.
[7] 肖恩邦,孙保平,陈串,等,陕北黄土区人工刺槐林地土壤水势特征[J].水土保持学报,2017,31(3):129-133.
[8]杜红普,刘波,王华军,等,基于土水特征曲线预测多孔介质毛细上升过程[J].工程地质学报,2013, 21(3):345-350.
[9]伍海兵,方海兰,彭红玲,等,典型新建绿地上海辰山植物园的土壤物理性质分析[J].水土保持學报,2012,26(6):85-90.
[10]CARDNER W R,HILLEL D, BENYAMINI Y.Post-IrrigationMovement of Soil Water:I.Redistribution[J].Water Resources Research, 1970,6(3):851-861.
[11]CARDNERW R,HILLEL D,BENYAMIM Y.Post-InigationMovement of Soil Water:P.Simulations Redistribution and Evaporation[J].Water Resources Rrsearch, 1970, 6(4):1114-1153.
