无黏性土坡滑动过程与接触网络演化分析

蒋炼　刘恩龙　田健秋　姜晓琼

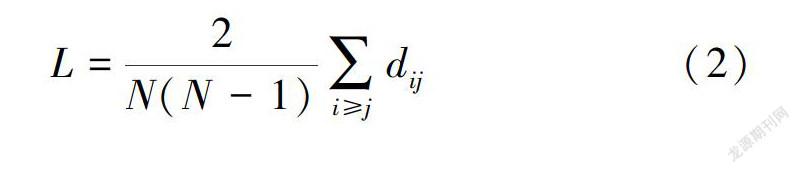
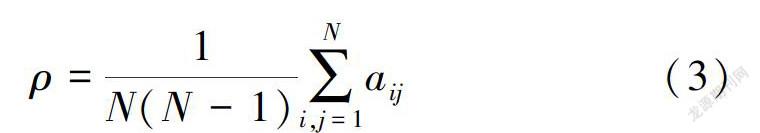
摘要：基于离散元法建立边坡模型，将颗粒间的黏结强度降低为零来模拟边坡的滑动过程。通过记录不同时间步下边坡的破坏形态，从复杂网络的视角分别对边坡坡顶、坡中和坡脚的平均度、平均最短路径和网络密度进行了分析。结果表明：靠近边坡表面的颗粒沿着斜坡向下运动，且越靠近坡面的颗粒位移变化越大;失稳后的斜坡通过初始边坡的中点，形成新的稳定边坡的坡面倾角略小于初始边坡双轴压缩试验得到的峰值应力内摩擦角;在初始滑动阶段坡顶、坡中和坡脚颗粒的平均度均减小，接触网络结构的稳定性减弱，初始阶段边坡的抗剪强度降低，很容易发生失稳变形;随着时间步的增加，坡顶颗粒的平均最短路径减小，坡脚颗粒的平均最短路径增大，坡顶颗粒比坡脚颗粒更容易进行信息交流;随着时间步的增加，坡顶的接触网络变得越来越稠密，坡脚的接触网络变得越来越稀疏，这是滑坡发生后坡脚处土体变得松散的原因。

关键词：接触网络;离散元法：边坡失稳;细观尺度;复杂网络

中图分类号：TU449

文献标志码：A

doi：10.3969/j.issn.1000-1379.2019.04.032

士坡失稳是一种常见的地质灾害，其失稳破坏是一个发展变化的过程，可分为局部失稳、整体失稳滑动、剧烈滑动破坏和滑动后稳定4个阶段。数值模拟方法被广泛应用于评估边坡工程的稳定性，研究边坡的破坏形态和坡体滑动规律，常用的方法有极限平衡法[1]、有限单元法和离散元法。基于连续介质力学的有限单元法很难描述土坡滑动过程，而基于离散单元法的研究仅给出坡体滑动的宏观规律[2]，比如运动速度、滑动距离等，没有提供坡体滑动过程中滑块之间的接触关系以及滑块的接触网络演化规律。传统的极限平衡法，如Bishop法[1]、Sarma法[3]等被广泛应用于分析边坡的稳定性，但有一定局限性。Clough等[4]最早将有限元法用于边坡的稳定性分析，郑颖人等[5]将有限元强度折减法应用于分析边坡稳定性。离散元法是一种基于非连续介质理论的数值方法，是Cundall[6]最早提出的，这种方法通过定义细观参数，不仅可以处理宏观问题，而且储存大量土体颗粒信息，因此被广泛应用于岩土问题分析。

尽管有学者对土坡的滑动过程和规律进行了大量研究[6-17]，但是已有研究的重点在坡体滑动的宏观现象描述上。现阶段基于复杂网络的分析方法仅用于分析密实试样压缩过程，而从复杂网络视角对边坡滑动过程中接触网络的演化分析鲜有研究。土坡作为一种复杂地质体，其不同部位的力学性质、位移规律等不同。基于此，运用离散元法建立土质边坡，从复杂网络的视角对边坡滑动过程中坡顶、坡中和坡脚的平均度、平均路径长度、网络密度进行研究，以期为坡体滑动的宏观规律进行有益补充。

1 无黏性土坡的颗粒流数值模拟

1.1 边坡模型建立

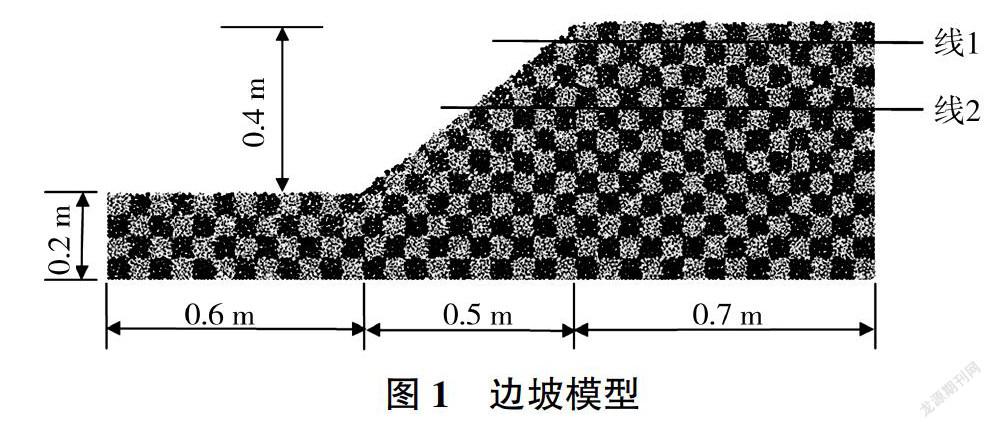
数值模拟采用接触黏结模型，颗粒的最小半径为3 mm、最大半径为6 mm，法向刚度为50 MPa、切向刚度为50 MPa.颗粒间初始接触强度为50 MPa、摩擦系数为0.3、初始孔隙率为0.16。相似于离心机模型，本次模拟采用放大的重力场法[18]，在200 9重力场下以0为坐标原点，向右为x轴正方向，向上为y轴正方向，建立平面直角坐标系，生成一个长1.8 m、高0.6 m的矩形模型。根据开挖的边坡形状，削去多余颗粒，生成边坡的斜率为0.8.坡顶为自由面，底部和侧面的墙无摩擦。为了观察颗粒的位移情况，对边坡划分网格并染色，网格边长约为0.05 m，一个网格含有约30个颗粒，生成边坡模型见图1。

边坡失稳的原因可以分为内摩擦角降低、黏聚力降低、孔隙水压力变化。为了简化模型，采用颗粒间接触强度为0来模拟无黏性土坡失稳[18]，并对坡体的滑动过程和接触网络的演化进行分析。

1.2 参数标定

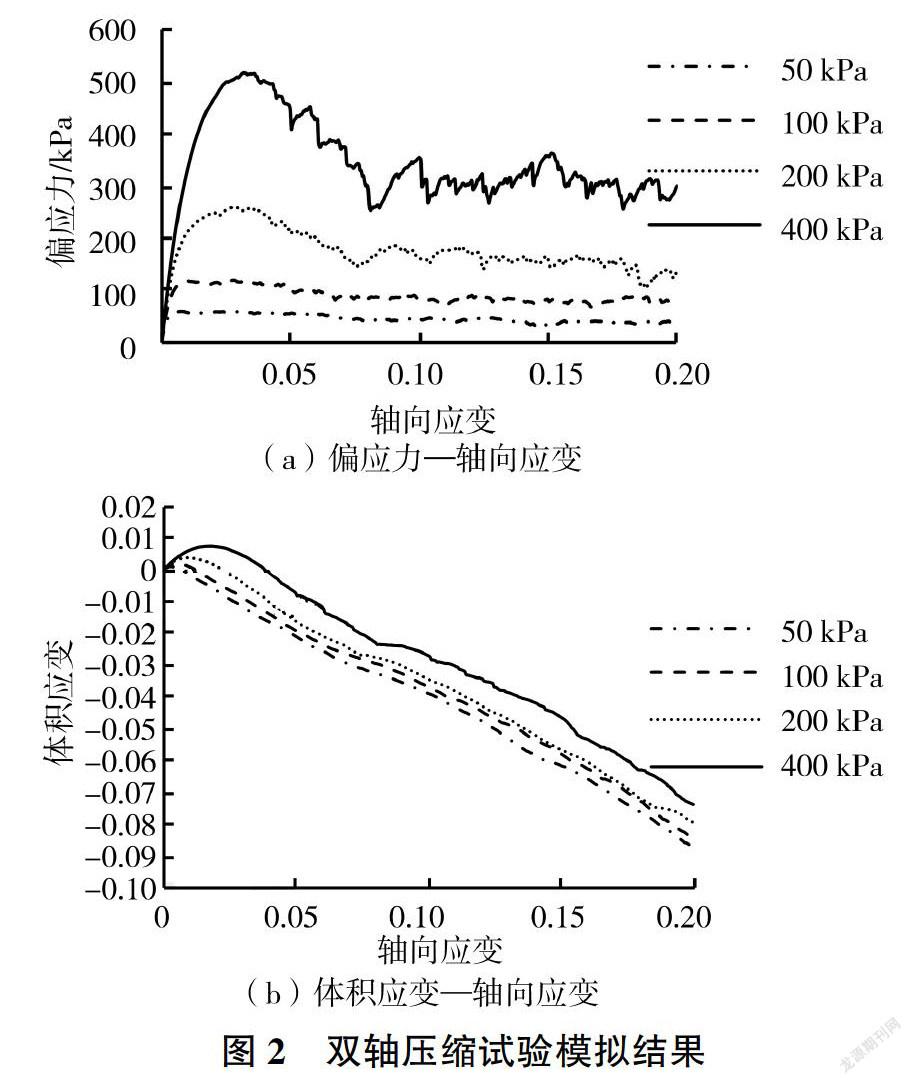
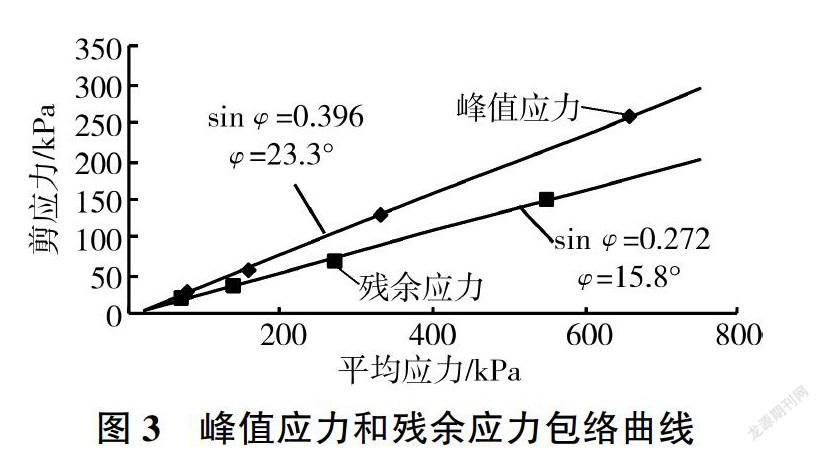
离散元法基于颗粒的细观力学参数进行计算，而细观力学参数不能直接与宏观力学联系，因此需要进行相应的数值试验将细观力学参数和宏观力学联系起来，进行双轴压缩试验。颗粒间接触强度为0的偏应力一轴向应变和体积应变一轴向应变关系曲线见图2。双轴压缩试验颗粒的尺寸与边坡颗粒的相同，双轴压缩试验的试样长度为0.4 m、高为0.8 m，初始孔隙率为0.16，生成约4 000个颗粒，在固结压力为50、100、200、400 kPa下的压缩应变速率为1%/min，当试样的轴向应变达到200-/0时停止压缩。双轴试验结果表明，试样在4种固结压力下均表现为应变软化。峰值应力和残余应力包络曲线见图3（φ为内摩擦角）。试样的峰值应力内摩擦角为23.30°残余应力内摩擦角为15.8°。

2 边坡失稳分析

2.1 变形特征

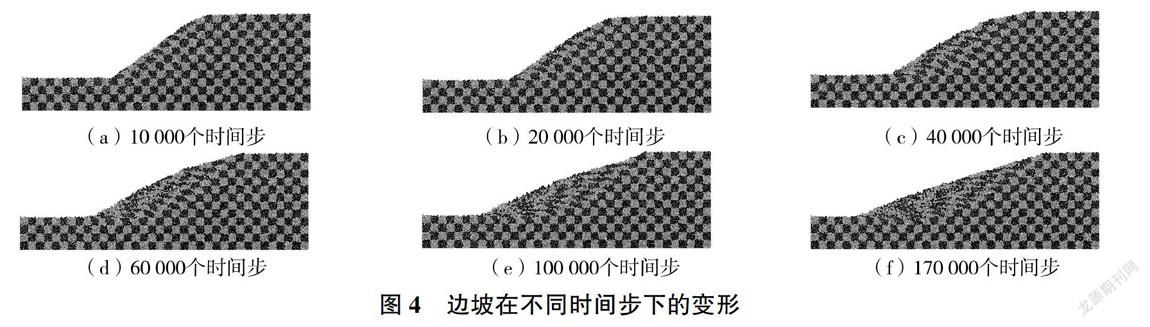
在颗粒间黏结强度降低为0的情况下，边坡滑动面的破坏形态见图4。图4（a）坡顶和坡脚发生了变形;图4（b）坡顶和坡脚发生了较大变形，坡脚的颗粒向前移动;图4（c） -图4（f）边坡的变形越来越大，边坡上部的颗粒向下滑动并带动下部的颗粒发生变形，部分网格被完全损坏，其中图4（f）失稳的边坡达到新的稳定，并可根据网格发生的变形，粗略地得到滑动面的位置。

2.2 位移分析

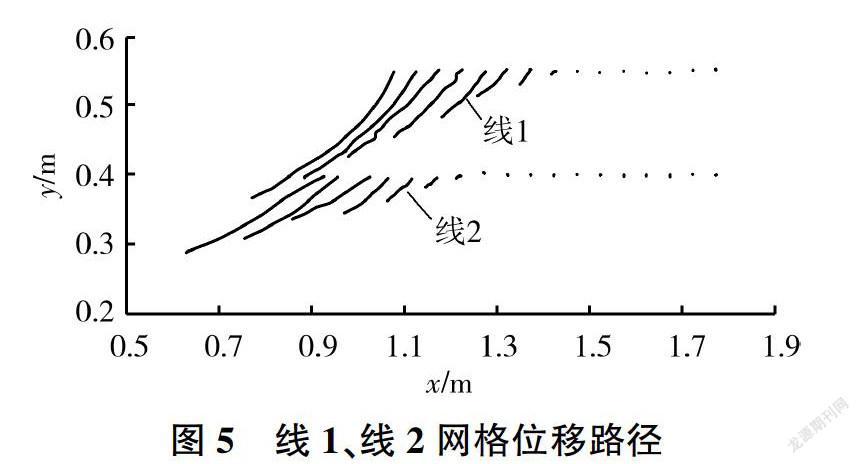
坡顶线1和坡中线2的位置见图1，对线上网格在边坡滑动过程中的位移路径以O为原点进行统计，见图5。由图5可知，失稳后网络节点的位置都低于初始位置。线1，x<1.35 m的网格节点沿着斜坡向下运动，x>1.53 m的网格节点向下轻微运动，越靠近坡面的网格节点位移越大：线2上的网格节点运动规律与线1类似。

2.3 失稳形状分析

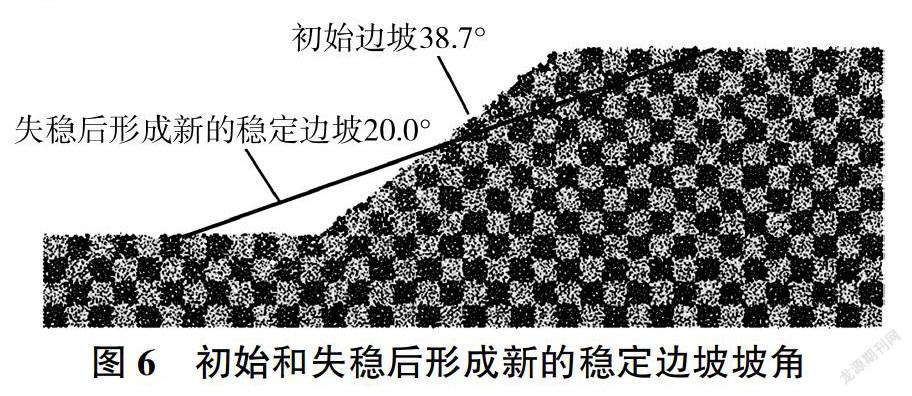
初始边坡失稳后，颗粒发生滑动，经过不断调整，最后达到新的稳定，失稳后形成新的穩定边坡的形状见图6。失稳后形成新的稳定边坡并没有经过初始边坡的坡脚，而是通过初始边坡的中点。失稳后形成新的稳定边坡的坡角为20.0°，略小于图3中双轴压缩试验的峰值应力内摩擦角23.3°，大于残余应力内摩擦角15.8°。

3 坡体滑动过程中细观参数演化

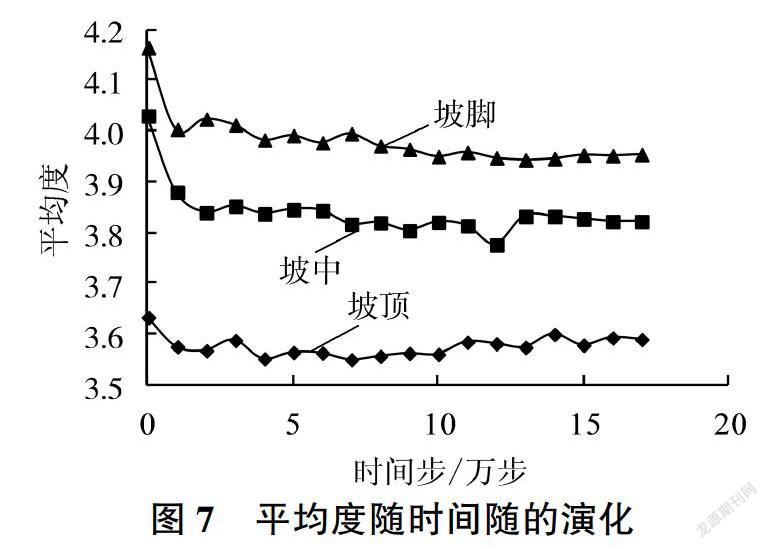
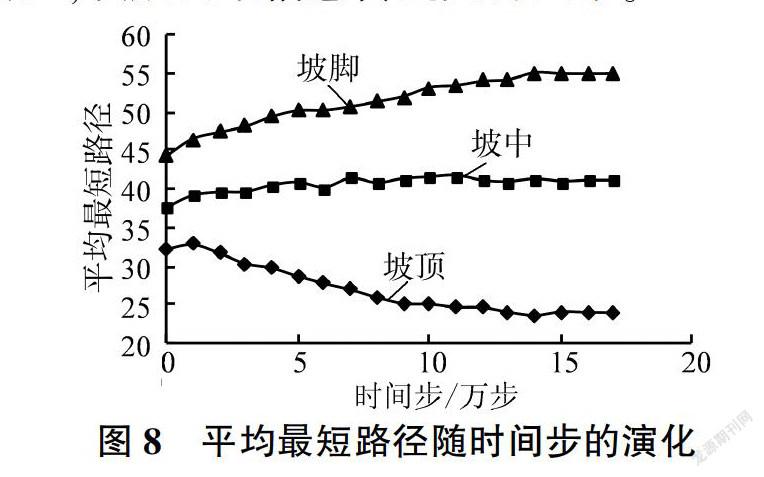
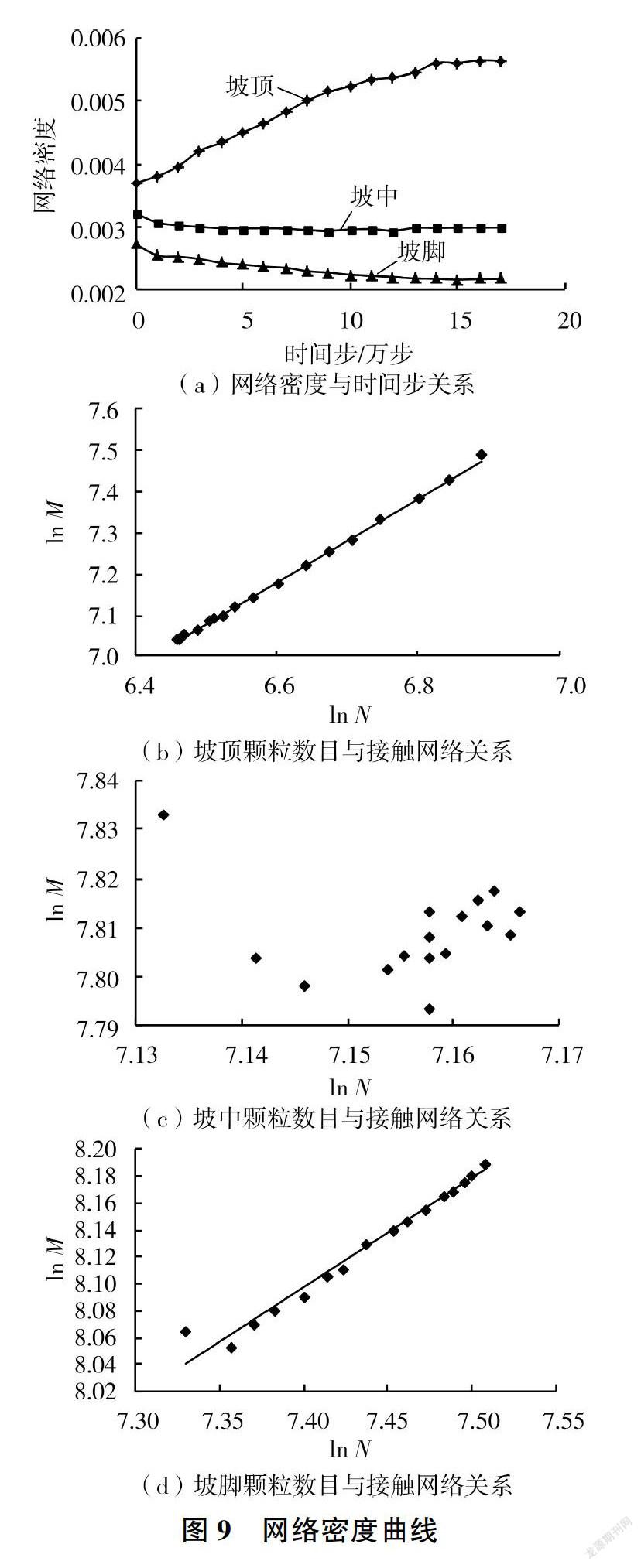
研究边坡内的颗粒时，可以将单个颗粒看成一个点，颗粒间的接触看成一条边，需要关注的是颗粒之间是否有接触，即两点之间是否有线连接，因此引入图论的概念对边坡进行分析。图论中的点称为顶点，连线称为边[19]。以y方向位置将边坡划分为坡顶（0.50 m

点度[20]是网络最基本的特征，指的是与点相关联的边数。网络中存在一小部分点度值较高的点被称为高点度点。高点度点越多，意味着网络中高点度点与其他点的联系越多，结构越稳定。平均度（k），也称为配位数，代表网络中点度的平均值，它和颗粒数目的关系为

坡顶、坡中和坡脚的平均度随时间步的演化见图7。由图7可知，坡顶、坡中和坡脚在初始滑动段（时间步为0-1万步）平均度均减小，接触网络的稳定性减弱，初始阶段边坡的抗剪强度降低，边坡易发生失稳变形。随着时间步的增加，由于边坡发生滑动，颗粒重新排列，因此平均度出现一定波动;当边坡达到新的稳定状态后，平均度不再随时间步发生变化。在发生滑动前，坡顶的平均度为3.63，坡中的平均度为4.03，坡脚的平均度为4.17：边坡达到新的稳定状态后，坡顶的平均度降低为3.59，坡中的平均度降低为3.82，坡脚的平均度降低为3.95。即边坡发生滑动时，坡顶的平均度变化最小，坡中次之，坡脚的平均度变化最大。出现这一现象的原因可能是，边坡滑动过程中，坡顶的颗粒向下滑动，未发生滑动的颗粒受扰动程度较小，因此坡顶的平均度变化最小：颗粒间的黏结强度为0，颗粒的平衡靠颗粒间的接触力，前面的颗粒滑下去后，后面的颗粒失去平衡，马上填补前面颗粒的空缺，颗粒在坡脚不断堆积，坡脚发生剪切破坏，颗粒間失去部分接触，大量颗粒重新排列，坡脚平均度变化最大。

3.2 平均最短路径

最短路径是指连接两个节点i和j之间边数最短的路径[21]，网络的平均最短路径（L）为任意两个节点之间距离的平均值，即

接触网络中平均最短路径可以反映接触网络之间信息的传递情况，平均最短路径越近接触网络之间信息传递越容易，平均最短路径越远接触网络之间信息传递越困难，因此研究坡顶、坡中和坡脚平均最短路径变化，见图8。从图8可以看出，随着时间步的增加，坡顶平均最短路径减小，坡脚平均最短路径不断增大，坡中平均最短路径略有增大但整体变化不大，这一现象与颗粒数目有关。颗粒数目越多，任意两个颗粒之间的距离越远，接触网络的信息传递越困难。坡顶颗粒数目减少，接触网络的信息传递变得容易;坡脚颗粒数目增多，接触网络信息传递变得困难。

3.3 网络密度

实际接触网络的规模随时间发生变化，因此引入网络密度来研究接触网络疏密性变化，见图9。网络密度（p）指接触网络中实际存在的边数与最大可能边数之比[22]，即

图9（a）表明，随着时间步的增加，坡顶颗粒的接触网络变得越来越稠密，坡脚颗粒的接触网络变得越来越稀疏，坡中颗粒接触网络的疏密性变化较小，且坡顶颗粒的接触网络比坡脚颗粒的接触网络相对稠密，主要原因是堆积在坡脚处的滑坡体多为松软土体。

由式（3）可知，网络密度与颗粒数目和接触网络的边数有关，因此对坡顶、坡中和坡脚的颗粒数目与接触网络的边数（M）进行统计，见图9（b） -图9（d）。

由图9可以看出，实际网络演化过程中，坡顶处颗粒数目和接触网络的边数呈线性变化，斜率为1.01，表明接触网络随着节点数的增加变得越来越稠密：坡中颗粒数目和接触网络边数的变化较为复杂，一方面坡顶颗粒向下滑动，引起坡中颗粒数目增加，另一方面其自身向坡脚滑动引起颗粒数目减少，因此接触网络的变化比较复杂：坡脚颗粒数目和接触网络的边数呈线性变化，斜率为0.83，表明接触网络随着节点数的增加变得越来越稀疏。

4 结论

（1）边坡发生破坏时，坡顶和坡脚的颗粒都发生滑动。靠近边坡表面的颗粒沿着斜坡向下运动，且越靠近坡面的颗粒位移变化越大。失稳后形成新的稳定边坡并没有经过初始边坡的坡脚，而是通过初始边坡的中点，失稳后形成新的稳定边坡的坡角略小于初始边坡双轴压缩试验得到的峰值应力内摩擦角，但大于残余应力内摩擦角。

（2）在初始滑动阶段坡顶、坡中和坡脚颗粒的平均度均减小，接触网络结构的稳定性减弱，初始阶段边坡的抗剪强度降低，边坡很容易发生失稳变形。随着时间步的增加，颗粒间发生滑动，平均度出现一定波动，当达到新的稳定状态后，平均度不再随时间步发生变化。边坡发生滑动时，坡顶的平均度变化最小，坡中次之，坡脚的平均度变化最大。

（3）随着时间步的增加，坡顶颗粒的平均最短路径减小，坡中颗粒的平均最短路径变化较小，坡脚颗粒的平均最短路径增大，即坡顶颗粒比坡脚颗粒更容易进行信息交流。

（4）坡顶和坡中接触网络密度随着时间步的增加而增大，坡脚接触网络密度随时间步的增加而减小，因此随着时间步的增加，坡顶和坡中接触网络变得越来越稠密，坡脚接触网络变得越来越稀疏，这是滑坡发生后坡脚处土体变得松散的原因。

参考文献：

[1]BISHOP A W.The Use of the Slip Circle in the Stability A—nalysis of Slopes[J]. Geotechnique， 1955，5（1）：7-17.

[2]WANG C，TANNANT D D，LILLY P A.Numerical Analysis ofthe Stability of Heavily Jointed Rock Slopes Using PFC2n[J].Intemational Joumal of Rock Mechanics&Mining Sciences，2003，40（3）：415-424.

[3] SARMA S K.Stability Analysis of Embankments and Slopes[J]. Joumal of Ceotechnical Engineering Division， 1979，105（12）：1511-1524.

[4] CLOUCH R W， WOODWARD R J.Analysis of EmbankmentStresses and Deformations[J].Soil Mechanics&FoundationDivision， 1967， 93（4）： 529-549.

[5] 郑颖人，赵尚毅，张鲁渝，用有限元强度折减法进行边坡稳定分析[J].中国工程科学，2002，4（10）：57-61.

[6]CUNDALL P A.A Computer Model for Simulating Progres-sive， Large-Scale Movements in Block Rock Systems[ C]//Nancy： Symposium of Intemational Society of Rock Mechan-ICS.1971： 8-11.

[7]CHEN H，LIU S H.Slope Failure Characteristics and Stabi-lization Methods[J].Canadian Ceotechnical Journal， 2007，44（4）：377-391.

[8]KIM J S，KIM J Y，LEE S R.Analysis of Soil Nailed EarthSlope by Discrete Element Method[ J]. Computers&Ceotechnics， 1997， 20（1）：1-14.

[9]JIANC M， JIANC T，CROSTA G B，et al.Modeling Failureof Jointed Rock Slope with Two Main Joint Sets Using aNovel DEM Bond Contact Model[J].Engineering Ceology，2015， 193：79-96.

[10]SCHOLTES L，DONZEF V.A DEM Analysis of Step-PathFailure in Jointed Rock Slopes[ J]. Comptes RendusMecanique， 2015（2）：155-165.

[11] 周健，王家全，曾遠，等，颗粒流强度折减法和重力增加法的边坡安全系数研究[J].岩土力学，2009， 30（6）：1549-1554.

[12]周健，王家全，曾远，等，土坡稳定分析的颗粒流模拟[J].岩土力学，2009，30（1）：86-90.

[13] 曾锃，张泽辉，杨宏丽，等，基于边坡渐进破坏特征对传统极限平衡法几点假设的合理分析[J].岩土力学，2012，33（增刊1）：146-150.

[14]ROTHENBURC L，KRUYT N P.Critical State and Evolu-tion of Coordination Number in Simulated CranularMaterials[J].Intemational Journal of Solids&Structures，2004， 41（ 21）： 5763-5774.

[15] PETERS J F，MUTHUSWAMY M， WIBOWO J，et al.Characterization of Force Chains in Cranular Material[J].Physical Review E，2005， 72（4）： 138-148.

[16]TORDESILLAS A，0'SULLIVAN P，WALKER D M， et al.Evolution of Functional Connectivity in Contact and ForceChain Networks： Feature Vectors，K- Cores and MinimalCycles[J].Comptes Rendus Mecanique， 2010， 338（ 10- 11）：556-569.

[17] SILBERT L E，CREST G S，LANDRY J W. Statistics ofthe Contact Network in Frictional and Frictionless CranularPackings[J].Physical Review E Statistical Nonlinear&Soft Matter Physics， 2002， 66（1）：114-129.

[18]JLANC M， MURAKAMI A.Distinct Element Method Ana-lyses of Idealized Bonded-Cranulate Cut Slope[J].Cranular Matter， 2012（ 14）： 393-410.

[19]李明哲，金俊，石瑞银，图论及其算法[M].北京：机械工业出版社，2010：4-5.

[20]DOROCOVTSEV S N， MENDES J F F.The Shortest Pathto Complex Networks[J].Physics， 2004， 71： 47-53.

[21]王小帆，李翔，陈关荣，网络科学导论[M].北京：高等教育出版社，2012：87-88.

[22]何大韧，刘宗华，汪秉宏，复杂系统与复杂网络[M].北京：高等教育出版社，2009：126-127.

【责任编辑吕艳梅】