城市干道交叉口联动控制优化建模

马庚华 郑长江 徐威 沈金星

摘 要：缓解干线道路交通拥堵问题，对于解决城市道路交通问题具有重要作用。通过综合考虑主路上下游交叉口和支路对系统的影响，针对车辆加减速延误、车辆停车延误、非协调相位的车辆延误三部分对干线道路协调相位进行讨论。建立了交叉口总延误模型，并通过遗传算法对延误模型进行求解，验证模型可行性。以期对交叉口延误研究提供一定价值的参考。

关键词：协调相位;遗传算法;延误

中图分类号：U491

文献标识码： A

随着我国经济的快速发展，当前车辆保有量逐年增加，拥堵问题严重影响了人们的出行。如何有效地解决交通问题，是提高城市发展速度的重要因素。干线道路在城市道路中起重要作用，当前针对城市干线优化最有效的方法，是对其进行协调控制，并且针对干线道路面对的不同情况，进行不同形式的优化。

LIU[1]开发MAXBAND-86模型，该模型用于解决城市干道路网的区域信号协调控制。WEBER[2]详细阐述了DOGS干道配时方法。我国的研究起步较晚，但经过多年的研究发展，国内学者对城市道路系统的研究获得了一定显著的成果。王志刚[3]建立车辆总延误最小为优化目标的干线交叉交通信号优化模型，该车辆总延误分别由干线方向的车辆延误和支路上的车辆延误组成。叶宝林[4]提出分布式模型用于預测大规模信号协调优化方案。郑远化[5]分析现阶段城市干道上尾气排放较为严重，所以首先建立了以公共周期、绿信比、相位差和相序为优化参数，以协调控制系统总延误最小化为目标的干道协调控制模型。

国内外学者应用系统工程等理论，在协调控制方面，得出很多优秀的模型和算法，但在干线道路协调相位和非协调相位的车辆延误方面仍有进一步研究的空间。

1 延误分类

本文考虑系统与上游交叉口、下游交叉口、支路之间的联系，建立对应系统总延误，再将研究目标分成三个部分进行讨论，分别为干线道路的协调相位车辆加减速延误;协调相位车辆的停车延误;非协调相位的延误。

2 建立交叉口延误模型

2.1 建立减速停车和启动加速延误模型

2.1.1 单车在交叉口受阻延误

如图2交叉口车辆行驶距离图所示，针对协调控制系统的研究，可知在车辆进入交叉口时，车辆从上游交叉口i到达交叉口i+1出现三种情况[6]，分别为①车辆不减速直接通过交叉口，车辆延误ds，a=0;②车队全部进行减速停车等待交叉口信号变化，在信号变化后进行加速通过交叉口;③车队尾部车辆进行减速停车等待信号交叉口的变化，然后加速通过交叉口。在②③情况下，协调相位上的车辆的行驶速度会从平均行驶速度减速为0和从0加速到平均行驶速度，此加速和减速过程会产生停车-启动延误ds，a≠0。

2.1.2 协调相位中受阻车辆数

在车辆全部受阻延误情况下，假设相邻交叉口i和i+1间的距离为li.i+1，交叉口i和i+1间车辆行驶平均速度为vi+1，交叉口i行驶到交叉口i+1的时间为ti=li.i+1vi+1[7]，记录车队第一辆车到达交叉口时的时刻为t2，绿灯放行时刻为t3，此段时间间隔为τi+1，相邻交叉口i到i+1的相位差为i+1，则有下面的公式：

在车辆全部受阻延误下，设第一辆车到达交叉口i的时间为ti，绿灯放行时刻为t3，该时段间隔为τi+1，可以表示为：

假设车辆到达交叉口的交通流量不变，即如图4所示，在t1时刻，信号灯由绿转为红。在t2时刻，上游交叉口车辆驶入当前交叉口，即到达交叉口的第一辆车因为红灯停车，车队开始积累;t3时刻当绿灯开始时，车辆开始通过停车线，t4时刻排队车辆全部通过停车线;t4到t5时段内交叉口通行能力大于车辆到达率，车辆可以直接通过交叉口没有延误。tred和tgreen分别表示红灯时间和绿灯时间，ti+1表示排队车辆全部通过交叉口所需时间，由于交叉口处于不饱和状态，所以ti+1<tgreen。

3 实例分析

3.1 研究对象选择

本文选取南京集庆门大街为研究对象，路段示意图如图5所示，各交叉口间距如表1所示，本文选取路段4个信号交叉口，交通流满足不饱和状态;在信号控制下，具有明显的脉冲型特征。为方便表达，对路口进行编号，其中AB的关联度为025-0.5;B-C、C-D关联度均大于0.5。

3.2 干线优化控制目标

本文拟采用遗传算法对目标函数进行求解[13]，干线优化目标函数为：

D=∑ni=2Di+∑n-1i=1Di+∑ni=1Di1（25）

最小、最大周期约束Cmin、Cmax分别取关键相位周期的0.75倍和1.5倍[14]。通过车流量的比值将非协调相位绿信比转换为协调相位绿信比：

λik=qik1-λi∑4k=2qik（26）

λi为协调相位第i个交叉口的绿信比，2≤k≤4。

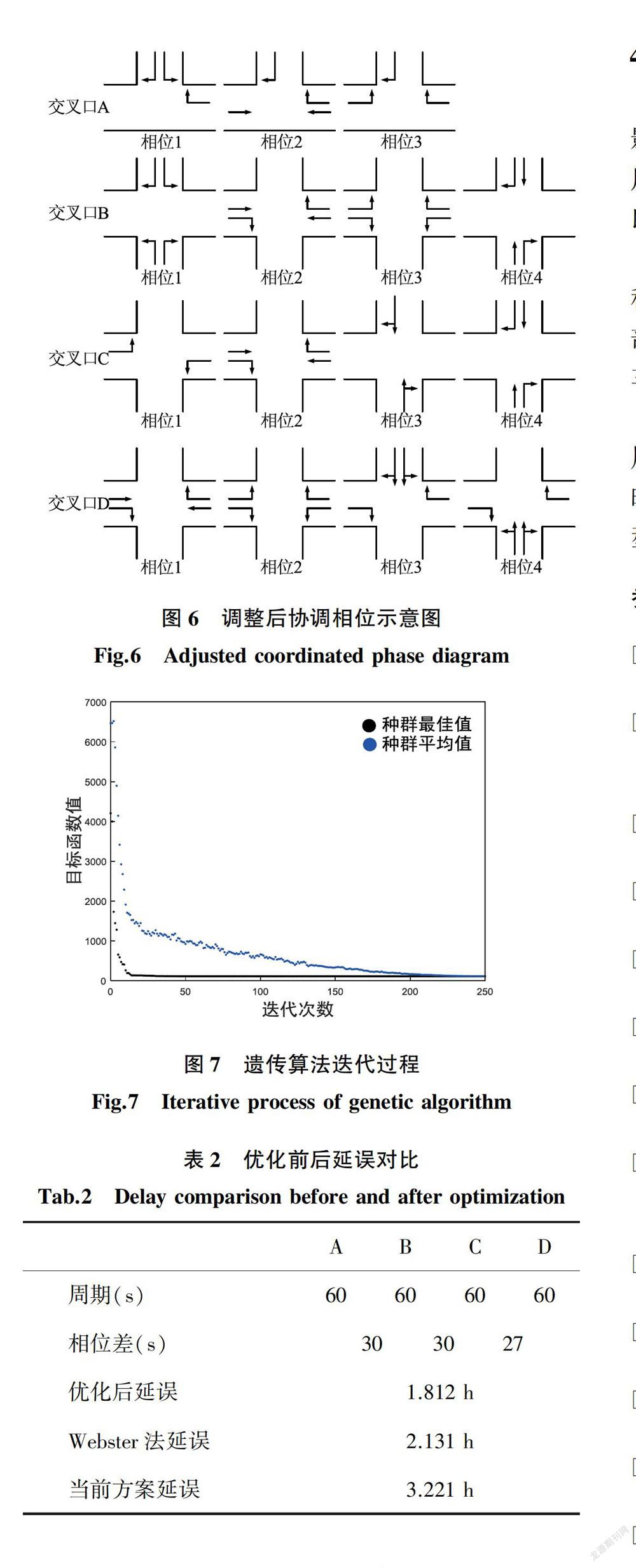
交叉口A为T型交叉口，B、C、D为十字交叉口，对当前信号相位进行调整，交叉口A、B相位时序不变，将交叉口C、D由5相位调整为4相位，调整后的协调相位如图6所示：

3.3 遗传算法求解

定义遗传算法种群为[C，λ1，…λn，1，…n]，基于Matlab编程求解[15]。随机生成初始种群，设定个体数为50，交叉概率0.8，变异概率0.2，250代遗传后停止迭代。

通过遗传算法可知，按本文优化方案，1 h内车辆总延误为108.72 min，即1.812 h。同时通过Webster法进行信号配时计算延误[16]，并通过交通调查计算当前配时方案延误，如表2所示：

4 结论

城市干线道路作为交通主要集流和疏散道路，影响整个城市的交通状况。本文通过实际调查，利用遗传算法对所建立的总延误模型进行求解，得到以下结论：

（1）协调相位的车队在未饱和交叉口产生三种情况：上游车队不减速通过交叉口;上游车队全部因为交通信号原因停车等待;上游车队前部不停车通过，车队后部停车等待。

（2）以最小延误为目标函数，计算最优解下的周期、相位差、总延误，并与Webster方案及现有配时方案进行对比，验证优化模型可行性，确定该模型可以有效降低干线交叉口总延误。

参考文献：

[1]LIU C. Bandwidth￣constrained delay optimization for signal systems[J]. Institute of Transportation Engineers， 1988， 58（12）： 21-26.

[2]WEBER A， LARSEN J， JORGENSEN R M . Green wave traffic optimization￣a survey[J]. Informatics and Mathematical Modelling，2008：102-123.

[3]王志刚. 干线交叉口交通信号协调控制[D].合肥：合肥工业大学，2014.

[4]叶宝林. 城市路网交通信号协调控制理论与方法研究[D].杭州：浙江大学，2015.

[5]郑远化. 考虑多车型排放特性的城市干道协调控制[D].大连：大连理工大学，2016.

[6]胡海涛， 罗杰. 基于相位差的子区交通信号协调优化控制[J]. 计算机技术与发展， 2018， 28（06）：157-161.

[7]荆彬彬， 徐建闽， 鄢小文. 适于双周期的干道绿波信号协调控制模型[J]. 交通运输系统工程与信息， 2018， 18（1）：73-80.

[8]路婷， 贝晓旭， 刘桂云. 基于交叉口重要度深度搜索的区域信号协调控制方法[J]. 交通运输系统工程与信息， 2018， 18（2）：80-86.

[9]賀冰花， 王润民， 安毅生. 基于GA-PDD的干线信号协调控制优化[J]. 测控技术， 2016， 35（11）：61-65.

[10]林华根. 城市道路交叉口信号协调优化控制研究[J]. 中国新技术新产品， 2016（3）：37-37.

[11]常在斌， 苏佳琳， 胡珍妮. 城市干道协调控制配时优化模型[J]. 价值工程， 2018， 37（24）：175-177.

[12]陈复扬， 闫啸岳， 姜斌. 过饱和状态下道路单交叉口的延误模型建立[J]. 物联网学报， 2017， 3（1）：40-46.

[13]梁小文. 考虑车辆在交叉口延误时间的干线协调控制研究[D]. 南昌：华东交通大学， 2018.

[14]曹涛涛， 蒋阳升， 赵斌. 考虑多交叉口相互影响的干道相位差仿真优化研究[J]. 工业工程， 2018， 21（6）：40-45.

[15]吴德华， 林毅. 基于混沌的汇流瓶颈区交通流模糊控制与仿真研究[J].贵州大学学报（自然科学版），2017，34（06）：110-114.

[16]张惠玲，杨林玉，敖谷昌. 信号交叉口延误参数获取综述[J].重庆交通大学学报（自然科学版），2017，36（03）：90-97.

（责任编辑：于慧梅）