连续混沌系统的修正函数投影同步及其电路仿真

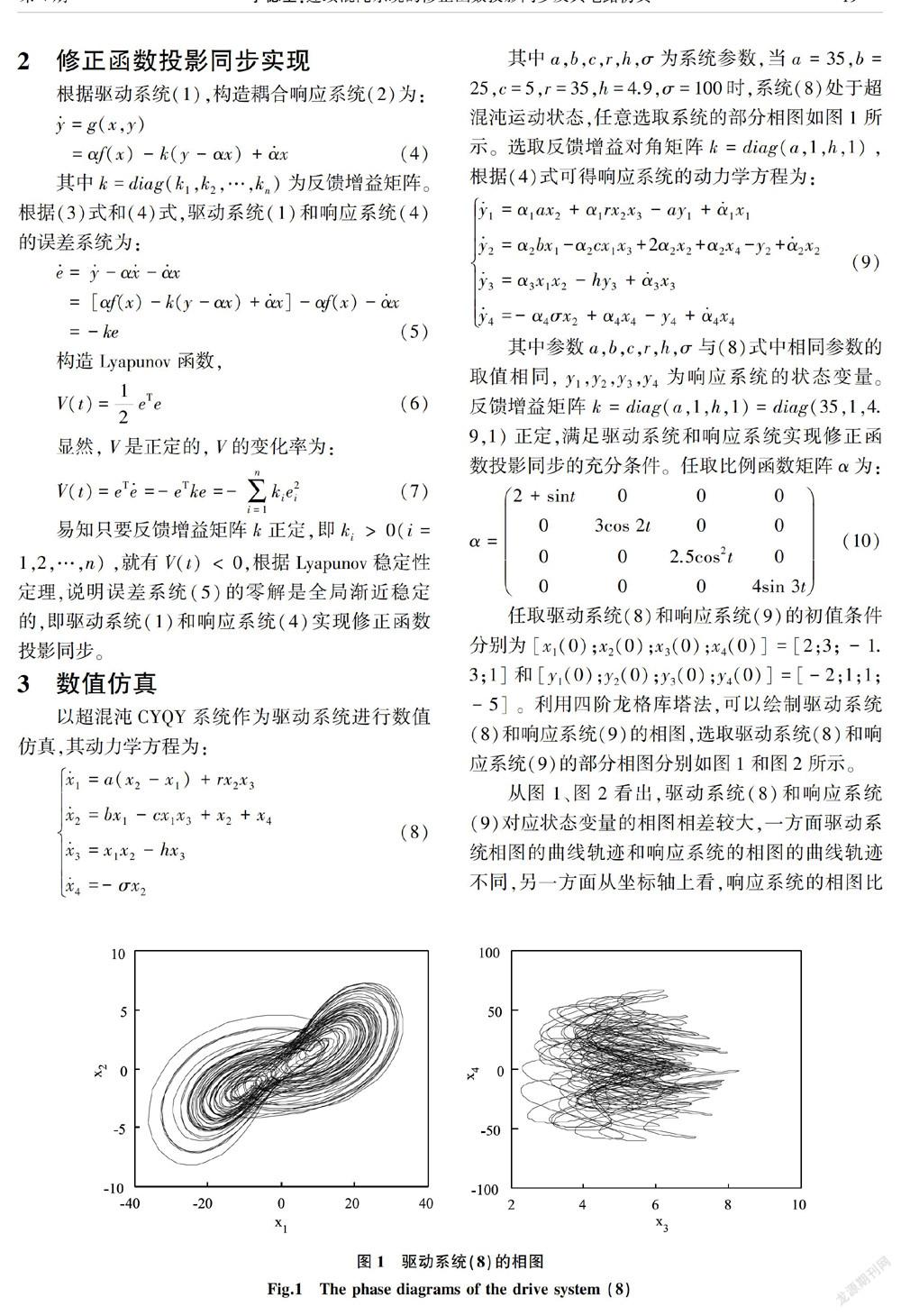
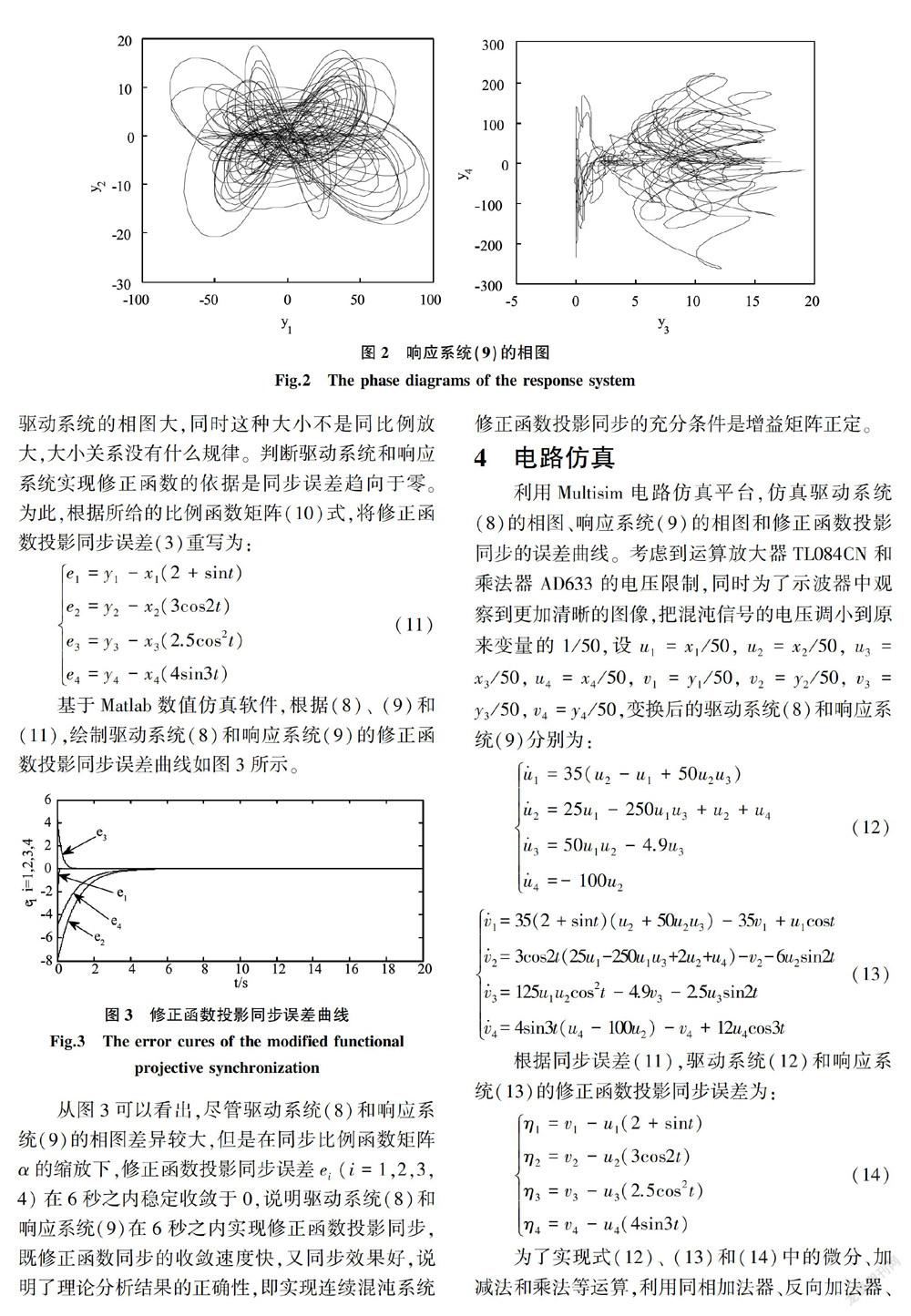
摘 要：混沌系统同步及其电路实现是混沌应用的前提和基础。为此，本文利用Lyapunov稳定性方法及运算放大器原理，研究连续混沌系统的修正函数投影同步及其电路实现问题。研究得出驅动系统和响应系统实现修正函数投影同步的充分条件是增益矩阵是正定的，同时数值仿真表明充分条件的正确性。示波器输出的波形图与数值仿真的一致，说明连续混沌系统修正函数投影同步的电路设计是正确的。

关键词：连续混沌系统;修正函数投影同步;电路仿真

中图分类号：O415.5

文献标识码： A

1990年，PECORA和CARROLL提出混沌同步概念[1]，为混沌在保密通信、非线性系统性能最优化、生态系统、人工神经网络、系统辨识和模式识别等领域的应用奠定了基础[2]。此后完全同步[3]、反同步[4]、广义同步[5]、投影同步[6-8]、函数投影同步[9-11]、修正函数投影同步[12-13]等混沌同步方式被广泛研究。修正函数投影同步是驱动系统和响应系统的不同变量对之间以不同的函数比例同步一致。所以修正函数投影同步不仅是最复杂的同步方式，也是完全同步、反同步、广义同步、投影同步、函数投影同步等的一般形式，也就是说如果驱动与响应系统之间满足修正函数投影同步条件，那么其他的同步方式也能够在驱动系统与响应系统之间实现。

混沌同步的电路实现是混沌应用的前提，近年来，混沌吸引子的电路设计与实现得到广大学者的青睐，主要表现在高维多翼混沌吸引子和分数阶混沌吸引子的电路设计[14-20]。然而研究混沌同步电路的文献很少，据作者所知，尤其是研究混沌系统修正函数投影同步的电路设计的文献几乎没有。为此，本文研究任意连续混沌系统的修正函数投影同步，同时基于Multisim电路仿真平台，设计四维超混沌系统CYQY的修正函数投影同步的仿真电路，为连续混沌系统的修正函数投影同步在保密通信中的应用奠定电路基础。

1 修正函数投影同步定义

5 结论

本文研究连续混沌系统修正函数投影同步的电路仿真问题，得到如下结论：

（1）得到连续混沌系统实现修正函数投影同步的一个充分条件：只要反馈增益矩阵正定，驱动-响应系统能实现修正函数投影同步，实现修正函数投影同步的条件简单且易满足。

（2）示波器输出的驱动系统相图、响应系统相图和时间序列波形图与数值仿真的一致，说明设计的修正函数投影同步的仿真电路是正确的，为连续混沌系统的修正函数投影同步在保密通信等领域的应用奠定了电路基础。

参考文献：

[1]PECORA L M， CARROLL T L. Synchronization in chaotic system[J]. Physical Review Letters，1990，64（4）： 821-824.

[2]TAO W， NUO J. Chaos control and hybrid projective synchronization of several new chaotic system[J]. Applied Mathematics and Computation， 2012， 218： 7231-7240.

[3]AGIZA H N. Chaos synchronization of Lü dynamical system[J]. Nonlinear Analysis， 2004， 58（1/2）：11-20.

[4]SAWALHA M M A， NOORANI M S M. Chaos reduced￣order anti￣synchronization of chaotic systems with fully unknown parameters[J]， Communications in Nonlinear Science and Numerical Simulation， 2012， 17（4）： 1908-1920.

[5]WANG Y W， GUAN Z H. Generalized synchronization of continuous chaotic system[J]. Chaos， Solitons & Fractals， 2006， 27（1）：97-101.

[6]LI G H. Modified projective synchronization of chaotic system[J]. Chaos Solitons & Fractals， 2007， 32 （5）： 1786-1790.

[7]HU M F. Full state hybrid projective synchronization of a general class of chaotic maps[J]. Communications in Nonlinear Science and Numerical Simulation， 2008， 13（4）： 782-789.

[8]HU M F， XU Z Y， ZHANG R. Full state hybrid projective synchronization in continuous￣time chaotic systems[J]. Communications in Nonlinear Science and Numerical Simulation， 2008， 13（2）： 456-464.

[9]DU H Y， ZENG Q S， WANG C H， et.al. Function projective synchronization in coupled chaotic systems[J]. Nonlinear Analysis： Real World Applications， 2010， 11（2）：705-712.

[10]HONG Y F. Adaptive function projective synchronization of time￣varying delay compex networks with definte integration scaling function[J]. 應用数学，2019，32（1）：242-252.

[11]陈镜伯，冯平，唐宏，等. 基于反馈调节函数投影同步的混沌保密通信研究[J]，计算机与数字工程，2017， 45（1）：20-23.

[12]李建芬， 李农. 一类混沌系统的修正函数投影同步[J].物理学报， 2011，60（8）：93-99.

[13]李德奎. 新超混沌系统的线性反馈修正投影同步的电路实现[J]. 海南大学学报， 2017， 35（4）：329-336.

[14]LAI Q， WANG L. Chaos， bifurcation， coexisting attractors and circuit design of a three-dimensional continuous autonomous system[J]. Optik￣International Journal for Light and Electron Optics， 2016， 127（13）： 5400-540.

[15]EL￣SAYED A M A， NOUR H M， ELSAID A， et.al. Circuit realization， bifurcations， chaos and hyperchaos in a new 4D system[J]. Applied Mathematics and Computation， 2014，239（15）： 333-345.

[16]黄露， 唐驾时. 五维混沌Chen系统的电路实现及其控制方法分析[J].湖南师范大学学报，2011，24（3）： 283-287.

[17]罗明伟，罗小华，李华青. 一类四维多翼混沌系统及其电路实现[J].物理学报，2013， 62（2）：161-166.

[18]黄沄. 一类多翼蝴蝶混沌吸引子及其电路实现[J]. 物理学报，2014， 63（8）：56-61.

[19]崔力，欧青立，徐兰霞. 分数阶Lorenz超混沌系统及其电路仿真[J].电子测量技术， 2010，33（5）：13-16.

[20]XU Z， ZHI J， LI D C. Dynamics， circuit implementation and synchronization of a new three￣dimensional fractional￣order chaotic system [J]. AEU￣International Journal of Electronics and Communications， 2017，82： 435-445.

（责任编辑：于慧梅）