基于BP神经网络的刻蚀偏差预测模型

胡浩儒 闫江 张永华

摘 要：刻蚀是将设计版图转化为到晶圆图形的重要步骤，刻蚀质量的好坏直接关系到芯片或集成电路的性能，而影响刻蚀质量（蚀刻偏差）的孔径效应和微负载效应在很大程度上取决于版图密度、图案间距等布局特征。为了探究在固定刻蚀工艺参数下的版图特征对刻蚀偏差影响，本文提出了基于BP神经网络的刻蚀偏差预测模型。首先，对一维版图的特征提取并建立用于训练模型和测试模型的训练集与测试集，然后，训练和优化该BP神经网络模型。实验结果表明，该模型预测值的绝对误差可达 ±2 nm 以下，而相对于真实刻蚀偏差的相对误差可达 10% 以下。因此在较大技术节点下，这种基于BP神经网络模型的预测精度是可以接受的。

关键词：刻蚀偏差;版图特征;BP神经网络;孔径效应;微负载效应

中图分类号：TN305.7;TP183

文献标识码： A

设计版图是通过光刻工艺制备在衬底上的。光线透过掩模照射在衬底表面的光刻胶上，激发光化学反应，显影后在光刻胶上留下所需要的图形（after development layout，ADI），如图1（a）所示。然而，光刻并不是将目标版图转移到晶圆上的最后一步。晶圆的刻蚀过程才是图形转移好坏的决定性步骤，它负责光刻胶上的图形转移到衬底上（after etching layout，AEI），如图1（a）。众所周知，到目前为止，刻蚀过程仍然无法用定量的物理化学模型来解释[1]。集成电路的最后关键尺寸是由光刻工艺与刻蚀工艺共同决定的。光刻胶上图形的图形尺寸与刻蚀后衬底上图形尺寸是有差别的，被称之为刻蚀偏差。大量实验数据表明，刻蚀偏差不是线性的[2]，它主要取决于两个因素：孔径效应和微负载效应。孔径效应是指刻蚀偏差与给定图形的线宽以及它们之间间隔有关。微负载效应是指刻蚀偏差与光刻胶上的图形密度有关[3]。在光刻行业中，通常将孔径效应与微负载效应称为刻蚀邻近效应[4]。注意，刻蚀偏差包括横向和纵向，横向偏差定义为刻蚀前后图形在晶圆平面内的线宽变化（ADI-AEI），如图1（b）所示;纵向偏差定义为刻蚀深度的差异，而本文侧重讨论横向偏差。

刻蚀偏差（特别是横向偏差）的出现将导致衬底上的图形不能准确反映光刻胶上的图形。为了保持刻蚀前后图形的一致性，由刻蚀引起的偏差必须加以修正。这种修正又称之为刻蚀邻近效应修正（EPC）[5]。刻蚀邻近效应修正就是在版图上，对目标图形预先引用刻蚀偏差，使之在光刻和刻蚀后在衬底上得到所需的目标尺寸。因此如何根据版图特征确定刻蚀偏差对于刻蚀邻近效应修正极其重要。

业界对于刻蚀效应的修正主要有两种，一种是基于规则（RB）的刻蚀修正;二是基于模型（MB）的刻蚀修正[6，7]。随着人工智能算法的发展，最近又提出了基于机器学习智能算法的刻蚀修正模型[8]。而人工神经网络作为智能算法的一种早已应用到计算光刻领域，如光学邻近效应修正（OPC）、氧化硅微沟道建模等[9，10]。

本文将介绍一种基于 BP（error back propagation）神經网络算法而建立一维版图预测刻蚀偏差模型。首先，我们对刻蚀前后的版图特征直接提取并整理分析，以建立数据集。其次，在该数据集上训练出基于BP神经网络的刻蚀偏差预测模型。最后使用该模型对新目标版图的刻蚀偏差进行预测，并对预测结果做简要分析。

1 BP神经网络算法与模型建立

1.1 BP神经网络算法

人工神经网络（artificial neural network，ANN）是受生物神经网络启发而建立的模型，其结构是由神经元和突触构成。在一般的多层神经网络结构中，包含输入层、输出层以及隐含层，在输出层和隐含层中包含有激活函数的神经元，每层神经元通过带有权值的连接线（连接权）逐层连接起来，如图2所示。

每个输入层节点接收可以反应研究问题本质的特征参数，它们的值被传播到第一隐含层的每个神经元节点，该隐含层的每个神经元的值为输入层的各个节点的值乘以其连接权的加权和。如果总和大于阈值，则隐藏节点输出为1，否则输出为0。阈值通常通过使用 sigmoid 函数来近似，该 sigmoid 函数输出介于0和1之间的浮点值。通过在每个隐含层重复以上过程，直到产生预测结果。其中 sigmoid 函数形式表示为：

BP网络算法的基本思想是：学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时，输入参数从输入层传入，经各隐含层逐层处理后，传向输出层。若输入层的实际输出与期望的输出不符，则转入误差的反向传播阶段。误差反传是将输出误差以某种形式通过隐含层向输入层逐层反传，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正各节点权值的依据[11]。正是这种误差反向传播使得各层权值不断调整，以达到网络学习的目的，从而确定个节点间的连接权值。

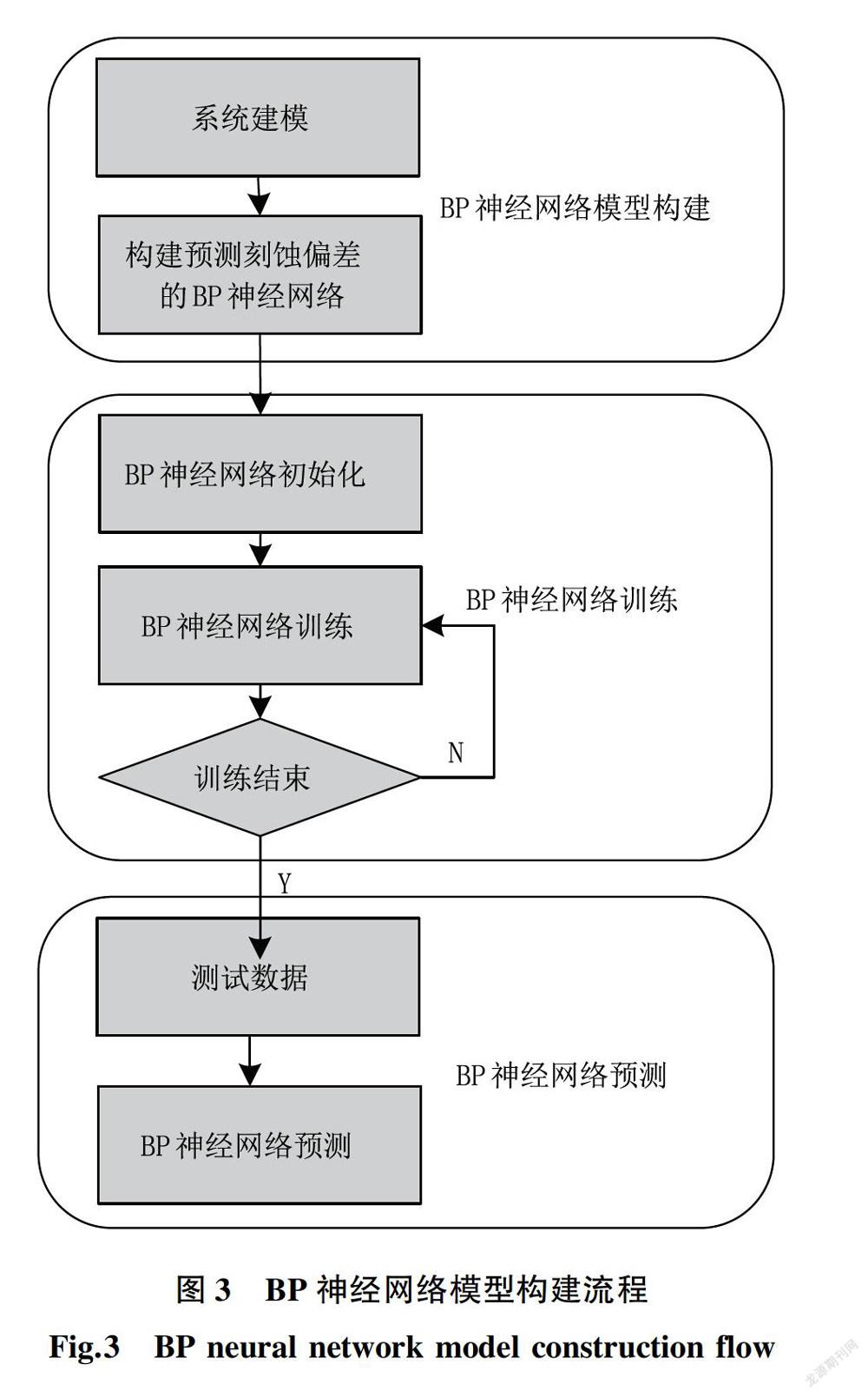
首先，BP神经网络模型构建要根据预测刻蚀偏差问题的特点确定BP神经网络结构，由于该预测刻蚀偏差模型有两个输入参数，一个输出参数，所以BP神经网络结构为 2￣x￣1 ，即输入层有2个结点，隐含层有x个节点，输出层有1个节点，其中隐含层需要根据刻蚀偏差具体问题而确定。

其次，BP 神经网络训练是根据设计版图上的版图特征而训练的，从而确立网络模型的各个参数。对于一维版图来说，它是由一组相互平行且具有间距的线组成。不同版图具有的间距和线宽各有不同。间隔和线宽之和被称为图形周期（pitch），线宽被称为关键尺寸（CD）。图形周期和线宽之比我们称之为图形占空比。不同的版图具有不同的图形占空比，它直接影响一维版图的图形密度。因此，具有不同的图形占空比也将影响刻蚀偏差大小。在本文中，我们从一维版图中提取对刻蚀偏差影响最大的关键因素，即pitch与 CD[13]。我们从不同的版图中提取图形周期和关键尺寸建立数据集作为BP神经网络输入层的输入参数，与此同时，把该版图与之对应的刻蚀偏差作为BP神经网络输出层的输出参数，如图4所示。为了建立用于模型训练与测试的数据集，我们从具有不同特征的版图中提取pitch、CD以及刻蚀偏差等数据，总共800组。随机选择其中750组作为训练集，用于训练BP神经网络。剩下的50组作为测试集，用于测试BP神经网络对刻蚀偏差的预测性能。

1.3 刻蚀偏差预测模型建立

为了评价BP神经网络模型对刻蚀偏差的预测效果，我们引入R2 性能指标来评价含有不同网络参数的BP神经网络模型。在此基础上根据R2 的结果对模型参数进行优化以达到最佳预测性能。R2的数学表达式为：

其中在（2）式中，y^（i） 表示BP神经网络模型的预测值，y（i） 表示刻蚀偏差实际值，y-表示刻蚀偏差实际值的平均值，m表示样本总数。当R2指标接近1.0时，表示此BP神经网络模型对刻蚀偏差预测性能是最好的;而当R2性能指标接近0.0时，表示此BP神经网络模型对刻蚀偏差预测性能是最差的[14]。因此，为了提高预测模型的R2性能指标，优化BP神经网络模型，我们使用网格搜索法对模型中的激励函数，隐含结点个数等模型参数优化。

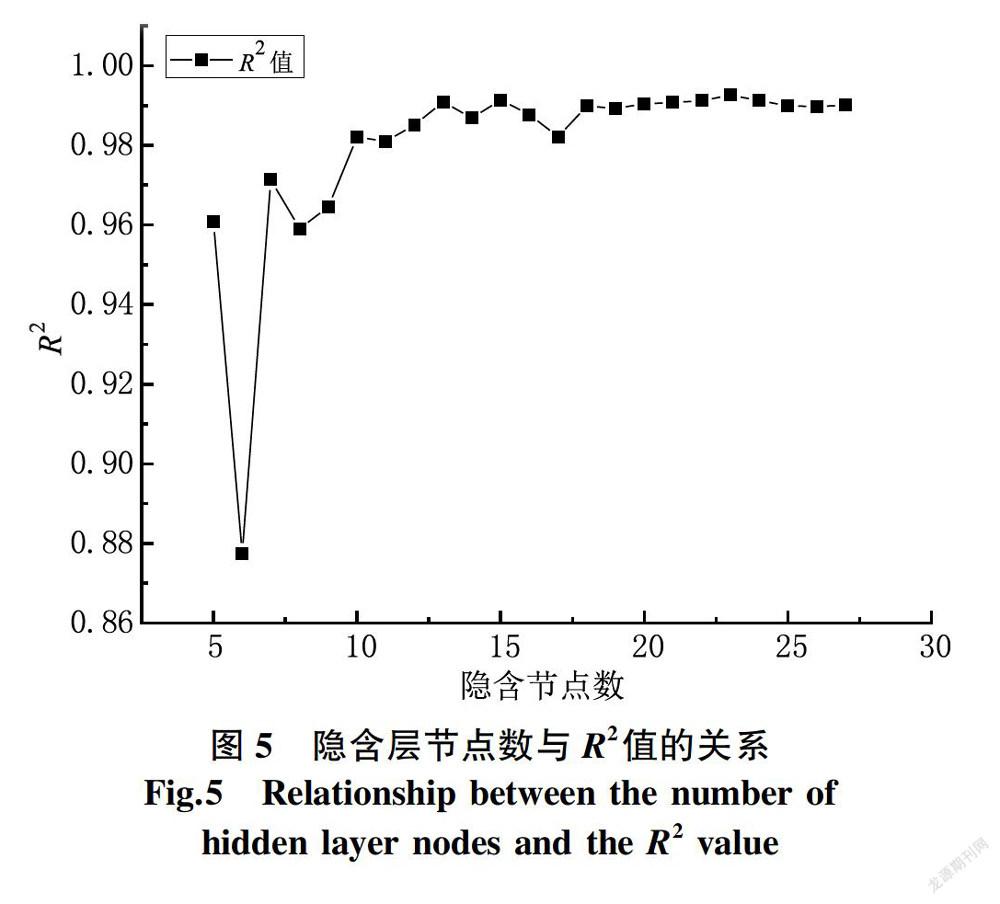
由于到目前为止，针对某一问题如何确立 BP神经网络的隐含层节点数没有较为准确的理论依据[15]，所以如何确定最佳的隐含层节点问题是构建预测刻蚀偏差的 BP神经网络模型的关键问题。为找到最合适的BP神经网络隐含层结点，预测模型使用含多个不同的隐含层节点数的网络结构，并在测试集进行测试。在此过程中，我们使用R2 性能指标对不同结构的网络的性能进行评价。我们使用23个不同网络结构模型以探索预测刻蚀偏差模型的最佳结构，其中每个模型的隐含层结点数目依次递增。由图5所示，可以看出随着隐含层的节点增加，R2性能指标也在不断增加，当隐含层节点数大于10时，R2指标逐渐趋于稳定且在0.98以上。而当隐含结点小于10时，R2性能指标波动比较大，不稳定。所以可以看出当模型中的隐含节点数目达到10左右时，该模型的预测性能是最好的。由于含有隐含层结点小于10的网络模型的鲁棒性比较差，而含有隐含层结点大于10的网络模型的训练时间会有所增加，所以该 BP神经网络模型选择含有10个隐含层结点的网络模型作为最优模型。

2 分析结果

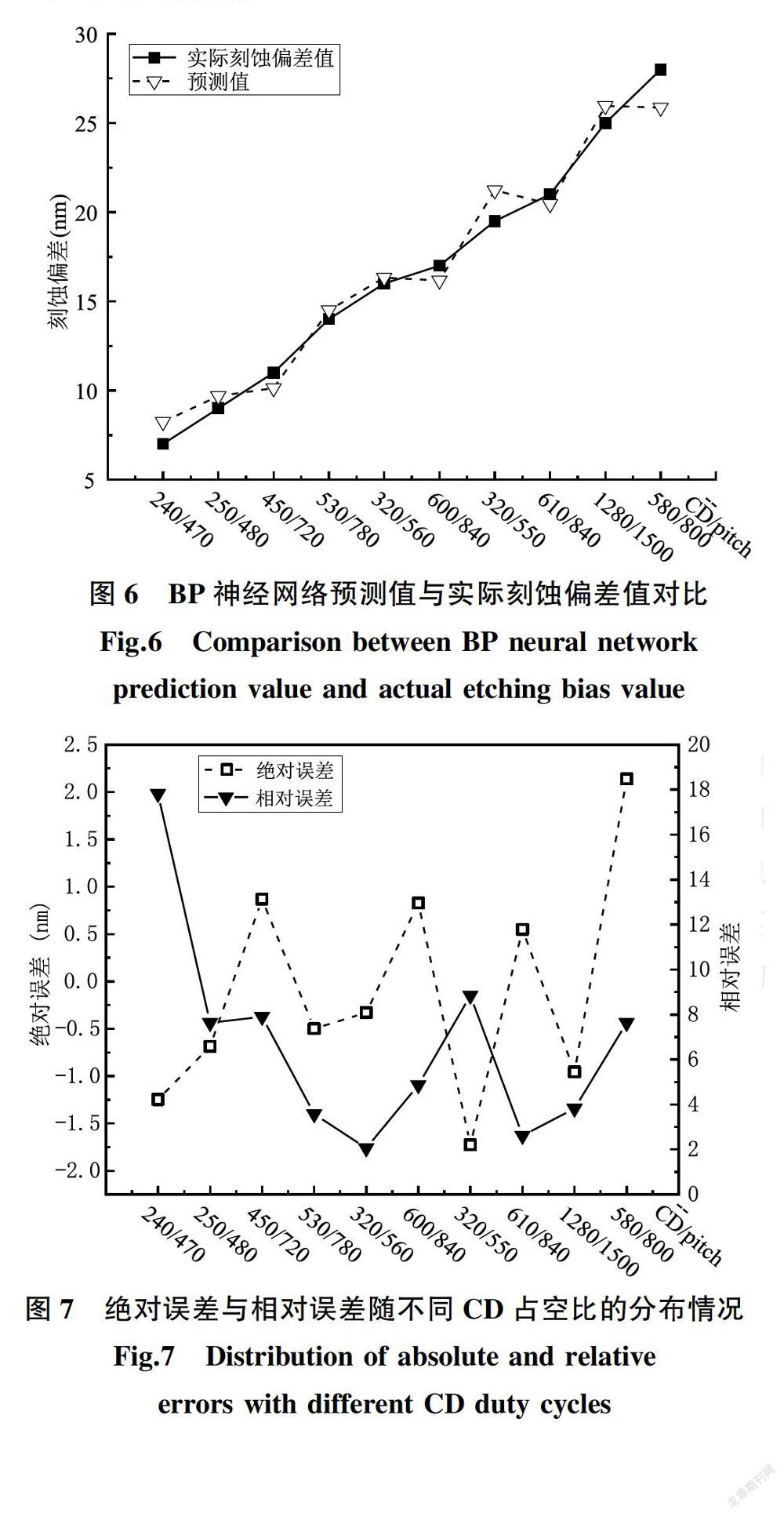
随后，我们随机选取10组含有不同pitch和 CD以验证优化后的模型对刻蚀偏差的预测效果。从图6可以看出，对于具有不同 CD占空比的版图，实际的刻蚀偏差与该模型的预测值在整体趋势是一致的。虽然在某些个别数据组中的真实值与预测值相差有些大，但二者在绝大多数情况下的差值是比较小的，说明对于一维版图该BP神经网络模型是比较能成功地拟合出由刻蚀负载效应而带来的刻蚀偏差。

3 结论

由于等离子体对晶圆刻蚀是极其复杂的反应过程，很难用一个或几个物理现象与化学现象去解释等离子的刻蚀行为，因此也就很难用准确的物理方程去拟合版图上的刻蚀偏差。相对于几百纳米的CD，该模型预测值绝对误差在 ±2 nm 以下，相对误差在10%以下。由此实验结果可以看出，在不需要了解过于复杂的等离子反应原理的情况下，使用BP神经网络预测具有一维特征的版图的刻蚀偏差是可行的，甚至在较大的技术节点是完全可以接受的。

参考文献：

[1]Stobert I， Dunn D. Etch correction， and OPC， a look at the current state and future of etch correction[J]. Proc. SPIE， 2013， 8685：868504-1-868504-11.

[2]SATO S， OZAWA K. Dry￣etch proximity function for model￣based OPC beyond 65-nm node[J]. Proc. SPIE， 2006， 6155：615504-1-615504-10.

[3]Jung S， Lo F， Yang T C， et al. Analysis of pattern density on process proximity compensation[J]. Proc. SPIE， 2007， 6520：652046-1-652046-11.

[4]Shang S， Granik Y， Niehoff M. Etch proximity correction by integrated model￣based retargeting and OPC flow[J]. Proc. SPIE， 2007， 6730：67302G-1-67302G-4.

[5]韦亚一.超大规模集成电路先进光刻理论与应用[M].北京：科学出版社，2016：358-359

[6]DRAPEAU M， BEALE D. Combined Resist and Etch Modeling and Correction for the 45nm Node[J]. Proc. SPIE， 2006， 6349：634921-1-634921-11.

[7]Liu Q， Cheng R， Zhang L. Study of model based etch bias retarget for OPC[J]. Proc. SPIE， 2010， 7640：76042T-1-76402T-6.

[8] Shim，Seongbo，S.Choi，et al.Machine learning （ML）-based lithography optimizations[C].Jeju， South Korea：2016 IEEE Asia Pacific Conference on Circuits and Systems， 2017.

[9]Luo R. Optical proximity correction using a multilayer perceptron neural network[J]. Journal of Optics， 2013， 15（7）：075708.

[10]Kim B， Lee B T. Prediction of silicon oxynitride plasma etching using a generalized regression neural network[J]. Journal of Applied Physics， 2005， 98（3）：034912-1-034912-6.

[11] 韓力群. 人工神经网络理论、设计及应用[M]. 北京：化学工业出版社， 2002：58-65.

[12]王小川. MATLAB神经网络43个案例分析[M]. 北京：北京航空航天大学出版社， 2013：11-12.

[13]Salama M， Hamouda A. Efficient etch bias compensation techniques for accurate on￣wafer patterning[J]. Proc. SPIE， 2015， 9427：94270X-1-94270X-7.

[14]Cameron A C， Windmeijer F A G. AnR￣squared measure of goodness of fit for some common nonlinear regression models[J]. Journal of Econometrics， 1997， 77（2）：329-342.

[15]周志华. 机器学习[M]. 北京：清华大学出版社， 2016：97-106.

（责任编辑：曾 晶）