ASIFT与SVD相结合的Contourlet域的抗几何攻击视频双水印算法

李智 陈淑琴 程欣宇 高奇

摘 要：为平衡数字水印技术中的鲁棒性与透明性，提出基于仿射尺度不变特征变换（ASIFT）与奇异值分解（SVD）结合的Contourlet域视频双水印算法。首先，利用卡尔曼滤波器将视频帧内的运动物体进行分离获取运动宏块，对运动宏块进行Contourlet变换;其次，利用奇异值分解对图像的信号攻击存在较高的稳定性和低频子带系数直方图在旋转、缩放等几何攻击具有较强的鲁棒性，自适应地将混沌水印序列分别嵌入到高频子带奇异值矩阵和低频子带系数中;最后，以ASIFT的尺度和方向不变性作为触发器，用于判断嵌有水印的视频遭受的攻击类型。本文算法能保证嵌入水印的视频帧的峰值信噪比值（PSNR）在70 dB以上，水印的嵌入量达到240×360 bit。实验结果表明本文的算法能够保证水印的不可见性的同时针对几何攻击和信号攻击都具有较强的鲁棒性。

关键词：仿射尺度不变特征变换;奇异值分解;Contourlet变换;双水印;抗几何攻击

中图分类号：TP309

文献标识码： A

随着互联网和信息技术的日益发展，保护数字多媒体作品版权、保证数字媒体信息安全的数字水印技术一直是热门研究方向，各种数字作品在其传输和使用过程中，必然会经历各种操作和攻击。几何攻击是视频水印系统众多攻击中最常见的一种攻击，它对含水印的数字作品全局或局部进行投影或者放射等变换。在几何攻击下，虽然水印仍存在于被攻击的数字作品中，但几何攻击已破坏水印与数字作品的同步性，从而导致检测失败。因此，几何攻击视频水印算法仍然是一个极富挑战的研究课题。

近年来，视频水印技术的研究取得很大的进展。2002年，DO等提出Contourlet变换[1]，克服了小波变换不能很好地捕捉图像几何特征的缺点。文献[2]把宿主图像变换至Contourlet域，采用多描述编码将高频子带分成奇描述子和偶描述子，将水印嵌入到奇描述子中;选择低频子带通过量化索引调制表来嵌入水印位。但该算法对于中值滤波、椒盐噪声及高斯噪声等常见的信号攻击水印提取效果不理想。文献[3]利用果蝇算法（Fruit Fly Optimization Algorithm， FOA）优化支持向量回归（Support Vector Regression， SVR）的参数，运用SVR算法结合Contourlet域自适应的嵌入水印。该算法能抵抗常规的攻击。但该算法的抗几何攻击能力不强，对旋转，剪切等常见攻击缺乏鲁棒性。文献[4]采用尺度不变特征变换（Scale Invariant Feature Transform， SIFT）提取特征点，得到圆形的特征区域，利用奇偶量化的方法将水印嵌入其中，但该算法仅局限在局部区域中保证水印能够抵抗几何攻击，但水印的嵌入量有待提高。文献[5]提出一种Contourlet域和奇异值分解（Singular Value Decomposition， SVD）相结合的方法，向高频子带能量值最高的前几个子带的奇异值中嵌入水印，该算法对常规的几何攻击具有一定的鲁棒性，但对旋转角度达到10°，20°时，水印提取存在失真。文献[3-7]均是单水印算法，單水印算法的优点是功能明确，但单水印算法功能单一，无法满足用户的多种要求，如果用户需要在版权保护的同时又需要对非法篡改进行检测，这时单水印就无法满足用户的要求，因此基于双水印的算法就产生。文献[8]在Contourlet域嵌入双水印，首先对低频子带系数进行SVD，在奇异值中嵌入水印，高频域考虑人眼视觉特性，把水印嵌入到人眼不容易察觉的区域，在不同子带中嵌入水印能抵抗不同的攻击，两个水印使所提出的算法提高了鲁棒性，但该文的水印嵌入容量有限。文献[9]利用SVD对原始水印进行处理，得到水印图像的奇异值矩阵，然后对四元数离散域奇异值矩阵中嵌入水印，该算法只能针对信号攻击。

本文提出一种基于仿射尺度不变特征变换（Affine Scale-invariant Feature Transform， ASIFT）与SVD相结合的Contourlet域视频双水印算法。本算法利用卡尔曼滤波器获取包含有运动物体的宏块，并对宏块进行Contourlet变换。然后，利用奇异值变换矩阵对常见信号攻击具有较高稳定性，对能量最大的高频子带进行奇异值变换并嵌入水印信息。由于低频子带系数直方图对几何攻击具有较强的稳定性，将水印信号嵌入到小波低频子带系数直方图中相邻系数级中。最后，运用ASIFT作为触发器判断视频帧是否遭受几何攻击。

1 算法的相关理论

1.1 Contourlet变换的基本原理

为了提高小波变换的多方向性和各向异性， 2002年提出Contourlet变换针对二维图像的表示方法。Contourlet变换是一种具有多分辨率、各向异性、多方向的影像表示方法。Contourlet变换与传统的小波变换相比具有多方向性的优势，使得其能更好的逼近奇异曲线。

Contourlet变换包括两个步骤：第一个步骤中，采用拉普拉斯塔（LP）的方法，将图像分为低、高频分量，以获取各分量中的奇异值点。第二个步骤中，通过方向滤波器组（DFB）按方向归入不同的系数带，形成轮廓波，这种方式使得轮廓波具有较优的非线性逼近性能。递归地进行第一步、第二步，即不断地将低频分量分解，然后用DFB 勾勒相关性的奇异值点，获得完整的Contourlet变换分解系数框架，如图1所示。

1.2 奇异值分解

在线性代数中有一种重要的矩阵分析和分解方法——奇异值分解。图像的奇异值体现了图像的内在特征，假设有一个矩阵A，对它进行SVD，可以得到3个矩阵：

式中：U和V均为正交阵;S=diag（λ1，λ2，…，λn）是奇异值对角矩阵，λ1，λ2，…，λn都是正值。奇异值本身具有强稳定性，抗扰动性极佳，且奇异值代表的不是人眼特征而是像素值的内蕴特征。

奇异值的内在特性仿真结果图2所示，其中，原视频帧如图2（a）所示，将该视频帧进行SVD分解，分别对视频帧进行旋转15°的攻击和放大1.2倍的攻击，用攻击后的图奇异值进行视频帧的重构，重构后的图如图2（b）（c）所示。

从图2可知，当图像旋转15°和放大1.2倍后，经过SVD重构后的图与原图无明显差异，从峰值信噪比值（PSNR）来看，旋转15°后的图像PSNR为46.61 dB，放大1.2倍后的图像PSNR为53.26 dB，表示基本无差别。综上可以看出奇异值分解的水印算法可以保护图像的稳定性、鲁棒性和透明性。

1.3 卡尔曼滤波器

目标跟踪是通过确定目标在视频图像中的位置信息来估计目标的运动状态，并预测下一个视频帧中目标物体的运动特性，然后通过所获得的特性匹配视频中的目标物体，从而达到连续准确跟踪目标的目的。目标检测的本质是从视频序列中将感兴趣目标提取出来。运用卡尔曼滤波器跟踪运动物体示意图如图3所示。

2 双水印嵌入框架

本文将视频帧进行卡尔曼滤波得到运动区域，将运动区域作为水印的嵌入部分。

2.1 高频水印嵌入算法

人眼在观察图像或视频时，通常会受到其它因素的影响，造成感知结果出现偏差，即存在视觉掩蔽特性。本文结合静态图像和视频帧序列中运动信息的人类视觉掩蔽特性，使视频水印具有较高的透明性和自适应性。

对于静态图像，图像的亮度敏感度f1、Contourlet域中不同频率的频率敏感度f2、以及纹理f3的掩蔽特性进行分析。

2.2 低频水印嵌入算法

文献[11]提出空间域的直方图在常见的几何攻击下具有不变性，并实验证明DWT的小波域低频子带也具有相同的不变性。我们可以用同样的方法证明Contourlet变换的低频子带也具有相同的不变性。本文采用如下步骤在低频子带嵌入水印：

（1）水印序列生成与高频子带部分相同。

（2）将视频帧的亮度分量Y进行Contourlet变换后得到低频子带。

（3）统计一个视频帧内的低频子带系数得到的直方图并求出低频子带系数的平均值avg。低频子带系数直方图中用于嵌入水印的区域X可以表示为X=[（1-α）avg，（1+α）avg]， 其中α是调节参数。为了将Lm个水印全部嵌入，X的宽度应该大于2×Lm。

（4）在区域X中，通过调整相邻两个柱状中系数的数量来嵌入水印。分别用A和B表示直方图中两个相邻的柱状区域，其中A中系数数量记为numA ，B中系数数量记为numB，则嵌入方法为ASIFT即仿射尺度不变特征变换算法，是MOREL J M和YU G S在2009年提出的一种特征提取改进算法[12]。由于SIFT算法没有完全的仿射不变性，使得其在提取匹配视角变换较大的图像特征点效果很不理想，ASIFT 算法在此基础上做了改进，来实现大仿射变形匹配，以满足应用的需要。由上节所述可知，由于ASIFT 特征点对图像处理攻击尤其是几何攻击均具有较好的稳定性和鲁棒性。因此，本文采用ASIFT 特征点计算仿射矩阵，得到仿射矩阵判断视频帧是否遭受几何攻击以及几何攻击的类型。利用仿射矩阵对几何攻击后的视频帧进行逆仿射变换以达到校正的目的。

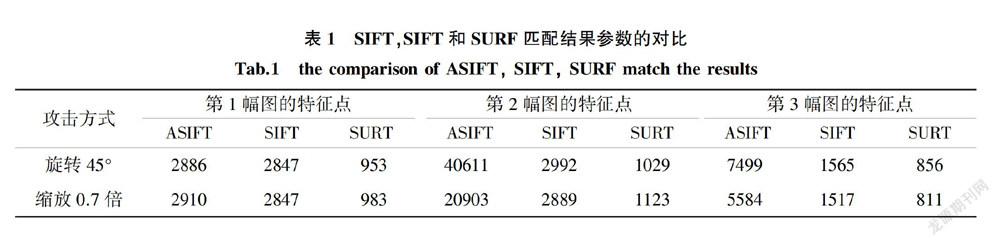
ASIFT的算法流程：首先导入两图分别作为查询图和训练图用作ASIFT匹配，对训练图进行各个经纬度模拟的仿射变换，经度Φ模拟通过直接旋转图像完成，而纬度θ模拟则通过对图像的水平方向二次采样（subsample）的方式;然后对查询图和完成变换后的训练图进行SIFT特征点提取以及进行匹配，得到的匹配点加入保存用容器（vector）中;如此模拟训练图所有的经纬度变换，再用SIFT提取它们的特征点并与查询图特征点匹配加入容器中，最后便可获得完整的ASIFT特征匹配点集。

实验结果可以看出ASIFT算法的正确匹配点数均高于SIFT算法、SURT算法所得的正确匹配点数。从而可得ASIFT能获取的匹配点远多于SIFT，和SURT，校正效果更精确。利用ASIFT尺度不变性提取的图像特征向量，通过对特征向量进行配准运算得到匹配点，利用多对匹配点获取仿射变换矩阵为

xy1=Ox′y′1=a11a12a13a21a22a23001x′y′1。（18）

利用仿射变换矩阵估计图像攻击前后的几何变换参数，恢复图像原始的信息，以及对应的水印序列。

4 双水印提取框架

4.1 高频水印提取算法

（1）首先判断视频帧是否遭受几何攻击，若遭受几何攻击，则先采用ASIFT校正视频帧再提取水印，反之则直接提取水印。

（2）水印的提取算法与嵌入算法互为逆过程。对加水印的图像I*进行Contourlet变换，分解得 到高频子带。

（3）对最高能量高频子带系数矩阵分别进行奇异值分解：

I*=U*S*V*T。（19）

（4）结合在嵌入过程中保存的S1，U2和V2矩阵信息，然后进行SVD的反过程：

U2S*V2T=C2。（20）

（5）用下式提取水印：

W*=（C2-S1）/JND（x，y）。（21）

（6）最后得到的水印位W*，用密鑰Key进行解调，得到最终恢复的水印信号。

（7）当所有视频帧的水印序列都提取后，将得到的所有水印序列进行统计。如果相同位置水印位为0的数量大于水印位为1的数量，则该位置水印位为0，反之则为1，最终得到最后的高频水印序列W。

4.2 低频水印提取算法

（1）与水印嵌入过程相同，对嵌入水印后视频帧进行Contourlet变换，统计全部低频子带系数得到直方图。

（2）在嵌入区域X中，分别用A*和B*表示直方图中两个相邻的柱状区域，其中A*中系数数量记为numA*，B*中系数数量记为numB*，则提取规则可以表示为

mei=1，numA*/numB*≥10，numA*/numB*<1。（22）

如果BER<τBER，则表示检测到了水印，用密钥Key恢复这帧视频中原始水印序列W*，反之则舍弃这一帧视频帧的结果。其中m*i为提取出的水印值，BER为位错率，τBER为提取水印的位错率阈值。BER的计算方法为

BER=1Lm∑Lmi=1m*imi。（23）

（3）将提取的所有水印序列进行统计，如果相同位置水印位为0的数量大于水印位为1的数量，则该位置水印位为0，反之则为1，最终得到最后的低频水印序列W。

5 实验结果

5.1 算法仿真

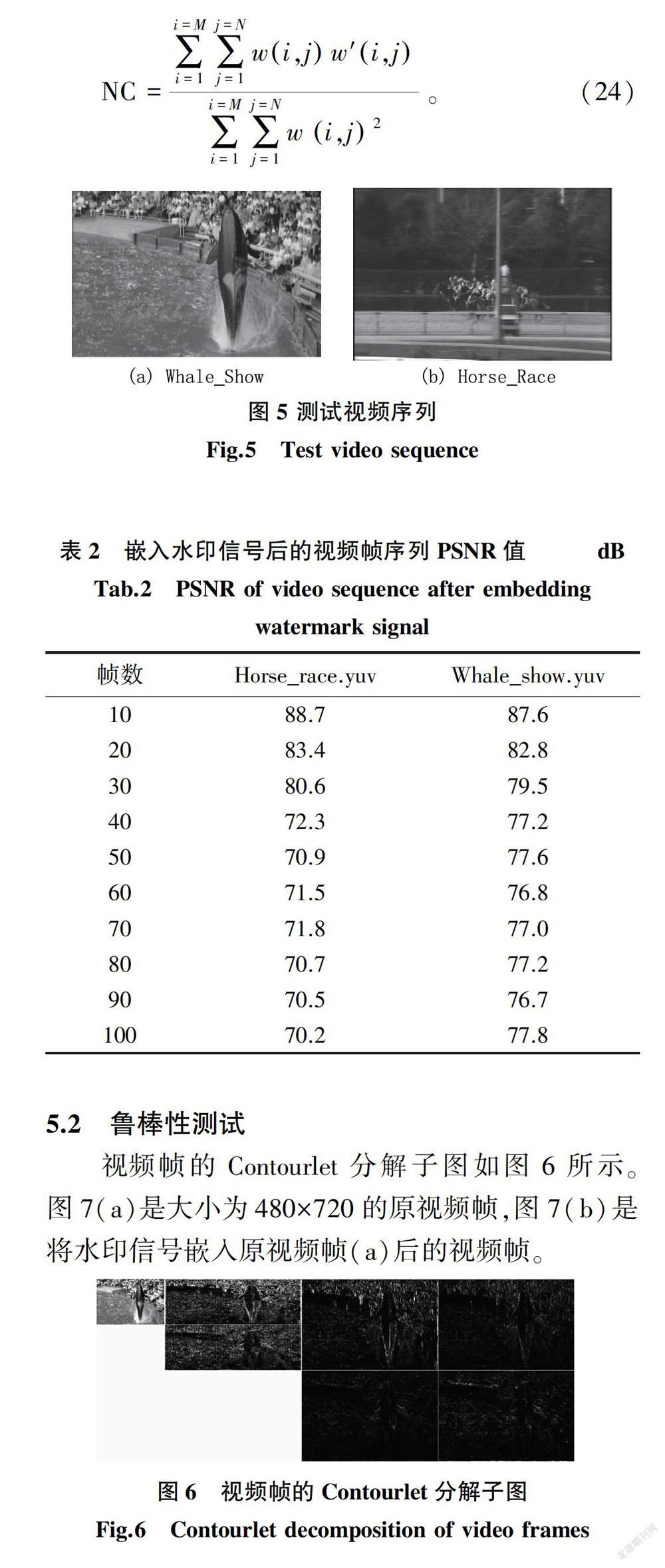
在仿真实验中选取两组100帧原始视频序列，视频的尺寸为480×720，仿真过程中对原视频帧进行2层Contourlet变换，塔式变换使用“5-3”滤波器和方向变换使用“pkva”滤波器。视频帧的contourlet子带分解图，如图5所示。PSNR用于客观地评价图像的质量，PSNR值越高，图像失真就越小。采用归一化相似度函数NC值来评价提取水印信号和原水印信号之间的相似度，NC值越大，代表水印的鲁棒性越高。利用相似性系数NC值来评价水印与原水印的相似度：

6 结语

本文提出基于ASIFT与SVD相结合的Contourlet域的视频双水印算法，首先，将视频帧进行卡尔曼滤波得到运动区域，对运动区域选取Contourlet域变换后得到的若干高频子带系数和一个低频子带，计算各个高频子带系数的能量值，选取最大

能量系数子带。然后，将该最大能量高频系数子带进行SVD分解，选取高频子带的整个奇异值矩阵作为嵌入区域，结合人眼视觉特性确定自适应嵌入强度，采用加性原则嵌入混沌水印序列;低频部分进行直方图的统计，利用contourlet低频系数直方图对常规几何变换具有近似不变性，调整contourlet域低频子带系数直方图中相邻柱状区域系数的数量自适应地嵌入水印信号。最后，采用ASIFT特征的尺度不变性和方向不变性的特点作为触发器，检验视频帧是否受到几何攻击，对遭到几何攻击的视频帧进行校正并提取水印，针对非几何攻击，采用高频部分的提取算法。通过一系列实验证明，本文算法在保持较高透明性的同时，对缩放、裁剪、长宽比改变等常见的几何攻击和非几何攻击均能具有较强的鲁棒性。因此，本文算法具有较好的鲁棒性和透明性。

参考文献：

[1]DO M N， VETTERLI M. Contourlets： a directional multiresolution image representation [C]// International Conference on Image Processing. Rochester： IEEE，2002：357-360.

[2]RANJBAR S， ZARGARI F， GHANBARI M. A highly robust two-stage contourlet-based digital image watermarking method [J]. Signal Processing： Image Communication， 2013， 28（10）：1526-1536.

[3]鲁荣波，陈留洋，丁雷，等.基于Contourlet域虚拟树结构和FOA-SVR的自适应鲁棒数字水印算法[J].电子学报，2017，45（3）：674-679.

[4]李雷达，郭宝龙，表金峰.基于奇偶量化的空域抗几何攻击图像水印算法[J]. 电子与信息学报， 2009，31（1）：134-138.

[5]毕洪波.鲁棒性数字图像与视频水印算法研究[D].北京：北京邮电大学， 2013.

[6]杨韫饴，王玲.非抽样Contourlet变换的低频数字水印[J]. 计算机工程与应用， 2011，47（16）：201-203.

[7]刘英， 王俊祥， 胡鸿豪，等.基于Contourlet变换和QR分解的鲁棒性盲数字水印算法[J]. 光电子·激光， 2016（3）：317-324.

[8]ZHANG J， YANG X， XIE X. Dual-watermarking algorithm based on Contourlet[C]// International Conference on Intelligent Control and Information Processing. Dalian： IEEE， 2010：213-216.

[9]陈善学， 冯银波. 基于四元数模型和奇异值分解的图像水印算法[J]. 计算机应用， 2013， 33（6）：1626-1629.

[10]LI Z， CHEN X W，MA J H. Adaptively imperceptible video watermarking based on the local motion entropy[J]. Multimedia Tools & Applications， 2015， 74（8）： 2781-2802.

[11]王丽云.抗几何攻击的视频水印算法研究[D].武汉：华中科技大学，2011：88-104..

[12]MOREL J M ， YU G S. ASIFT： A New Framework for Fully Affine Invariant Image Comparison[J]. SIAM Journal on Imaging Sciences， 2009， 2（2）：438-469.

[13]AGILANDEESWARI L， GANESAN K. RST invariant robust video watermarking algorithm using quaternion curvelet transform[J]. Multimedia Tools & Applications， 2018（4）：1-44.

[14]SINGH K M. A robust rotation resilient video watermarking scheme based on the SIFT[J]. Multimedia Tools & Applications， 2017（18）：1-26.

[15]陳淑琴， 李智， 程欣宇，等. 人眼视觉特性与SIFT相结合的视频双水印算法[J]. 计算机应用， 2017， 37（7）：1936-1942.

（责任编辑：周晓南）