关于圆中角平分线问题的一点思考

何怿熹

【摘 要】初三对圆的教学而言，是一个难点，又是一个重点。它往往会综合初中阶段所有的几何知识。学生往往在解题时碰到与圆相关的问题时，特别是做到成都市中考题的第2、3问总有一种苦不堪言的感觉，中下水平的学生更是无从下手，看到此题便各种畏惧，老师教学时学生听不懂也往往总是一声叹息。但是每每看到学生把圆问题的3问解出来后脸上的那种喜悦与亢奋愈发激发了我要与学生共同探究共同攻克难关的决心。当然，首先从我做起，分享下与学生共同探究，一题多解的过程，也谈谈在圆教学中碰到的最多的角平分线问题给我的一些思考。

【关键词】角平分线;模型;圆

【中图分类号】G633.6  【文献标识码】A  【文章编号】1671-8437（2019）28-0041-03

1   圆中角平分线模型图的建立

圆中的性质定理特别多，但是分类下来无外乎就涉及角、弧、线段三方面的位置关系和数量关系，研究其本身图形特点及与其三角形、四边形的综合问题时实际也是从这三方面出发，只是探究其彼此之间更深层次的关系而已[1]。于是我把初三阶段用得比较多的圆中角平分线问题做了一个关系梳理，引导学生从基本图形中挖掘出常见的结论以及已学的性质定理、基础模型图等综合形成圆中角平分线模型图，并将其迁移至实际解题中去。

1.1  有直径，圆中角平分线平分锐角

基本模型及基本结论：

此模型的结论也是看图分析的过程，从角的关系到线的位置和数量关系以及线段的组合关系都给了各种知识的交互使用，可以在后面很多圆的题型中剥离出此模型图的分支来，学生在解题时可运用模型图的思考迅速地识图并找到对应关系，快速解题。

1.2  有直径，圆中角平分线平分直角

基本模型及基本结论：

此模型在上一模型的基础上拓展延伸，从角的关系到线的位置数量关系，以及特殊三角形，全等图形的构造，旋转的运用，可以关联到图形中面积恒等即定值的问题。融合了多种图形的分析思路，当把此图作为模型图给学生分析透后，学生自然会感受在复杂图形中抽丝剥茧还原到我们最原始的基本图形中来。

2   圆中角平分线模型的运用

例题：图2，半圆⊙O的直径AC=6 cm，弦AB=10 cm，将半圆沿着过点A的直线折叠，折叠后使得弦AC恰好落在直径AB上，则折痕AD的长为____cm.

此题看似属于翻折问题，但是不同于之前三角形和四边形的翻折过程会出现线段相等，实质上AD就是圆中∠CAB的角平分线，即∠CAD=∠DAB，如何对这个题给学生做分析，我做了如下引导：

（1）从角的关系出发：两角相等，由圆中角的性质来看，两角均属于圆周角，因此可利用转换思想考虑弧等对应的圆心角与圆周角的关系。

法一：①首先在等弧条件下，2倍弧所对的圆周角=1倍弧所对的圆心角，这个其实也是基本模型图1中第（1）（2）条的结合。

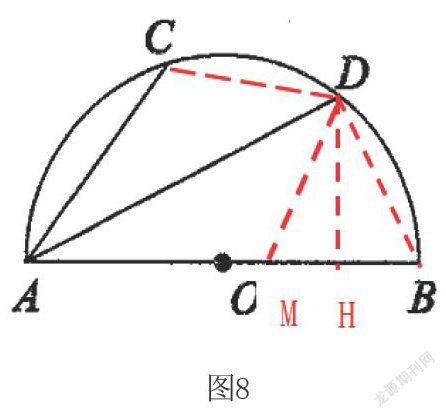
具体做法：连接BC、OD交于点M，过点D做DH⊥AB于点H，由∠CAD=∠DAB推其圆周角所对的弧等，再充分利用等弧条件下：2倍弧所对的圆周角=1倍弧所对的圆心角，得到等角关系，最后在RT⊿ACB=90º利用勾股定理以及三角函数的关系求得DH、OH的长。

法二：②由上述的角等可推线平行，再用平行线分线段成比例也就回归到我们圆中角平分线基本模型图1中的第5条，中位线的原型即显露出来，再利用勾股定理来解决就显得非常顺畅了。

具体做法：连接DB，可由∠CAB=∠DOB推得OM∥AC，再由平行线分线段成比例推得OM为⊿ABC的中位线，求得OM、BM和DM的长度，此时在Rt⊿DMB中，运用勾股定理可求DB长度，最后在Rt⊿ADB中，求得AD长度。

法三：③沿着法二中平行线的思路可联想到利用平行线构造相似图形，而过圆上的点同时向直径作垂线构相似的同时还会出现我们的射影模型图。

具体作法：过点D作DM⊥AB，过点C作CH⊥AB于点H，可发现⊿ACH∽⊿ODM，运用相似比或者借助三角函数均可求出DM的长度，此时再由CH⊥AB，“双垂型”的模型便显而易见了，射影定理AC2=AH·AB可轻松的求得AH的长度，这样一来OM的长度自然迎刃而解，最后回归法一的Rt⊿ADH中，勾股定理求得AD。

（2）从线段的角度来看：线段AD的本质即角平分线，在初中阶段，涉及角平分线的知识无外乎两点：一是角平分线性质定理的运用，二是其三线合一的知识的

运用。

法四：①由角平分线性质定理：角平分线上一点到角两边的距离相等，可构造出全等三角形，回归基本模型图1的第（6）（8）条。

具体做法：连接BC后与AD交于点Q，过点Q做QH⊥AB于点H，此时角平分线产生的全等图形⊿ACQ≌⊿AHQ，AH=AC=6，BH=4，可设CQ=QH=a，则BQ=8-a，在Rt⊿BHQ中，可得勾股方程求得a的值，在Rt⊿ACQ中AQ的长度勾股定理也可求，再连接BD，利用同弧所对圆周角相等关系结合三角函数求得DQ。

法五：②利用等弧和等腰三角形性质构造全等三角形，再利用三线合一构造射影模型。

具体做法：连接CD，在AB上截取AM=AC，连接DM，此时的全等三角形⊿ACD和⊿AMD便構造出来，AM=AC=6，DM=CD，再连接BD，由∠CAD和∠DAB两圆周角等对弧等，再对弦CD=BD，可知⊿MDB为等腰三角形，此时考虑三线合一的知识过点D做DH⊥AB于点H就显得非常顺畅了，MH=BH=2及AH=8也能轻松求解。同时“双垂型”的模型又再次凸显出来，利用射影定理AD2=AH·AB求AD便不再是难事。

法六：③在构造全等和射影定理的运用中我们又可以发现对∠ADB=90º的运用，简而言之，AD在做角平分线的同时还出现垂直关系，我们不妨把AD看成BD的高线，那三线合一构造等腰三角形的思路便逐渐清晰起来，也就是回归到我们基本模型图1的第（7）（8）条。这样一来全等图形，射影模型就都一一呈现出来。

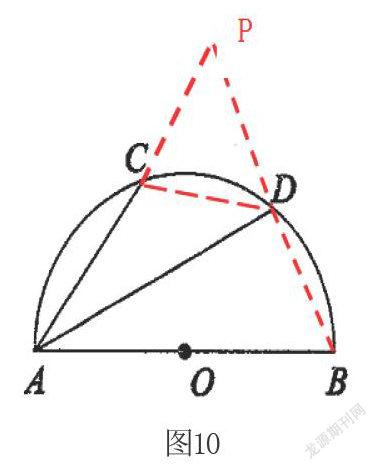
具体作法：在法五的基础上延长BD、AC交于点P，此时的⊿ABP即为等腰三角形，可得AP=AB=10，CP=4，PD=DB，由法五的CD=DB，又会发现⊿CDP为等腰三角形，再过点D做DM⊥AP于点M，三线合一得CM=MP=2，结合角平分线性质定理易得DM=DH，从而找到全等三角形⊿MPD≌⊿HBD，推得BH=MP=2，AH=8，最后回归⊿ADB中利用射影定理求AD。

法七：④用基本模型图1的第（7）条，由A、B、C、D为圆上四点，结合AD既做角平分线又做高线的特点，会发现圆内接四边形，这样借助圆内接四边形外角等于内对角的性质找相似三角形，可将求解过程大大简化。

具体做法：延长BD、AC交于点P后，连接CD，由圆内接

四边形性质，易证⊿PCD∽⊿PBA，得，再求出BD的长度，AD长也自然易求了。

法八：⑤用基本模型图1的第（7）条，由直径所对圆周角为90º，圆上两点分别与直径端点相连时均会构造出直角三角形，结合之前三线合一出现的等腰三角形⊿ABP来考虑。

具体做法：将法七中的连接CD换成连接BC，放在Rt⊿PCB中，AP=AB=10，AC=6，CP=4，BC=8，勾股定理可求PB的长，再由PD=DB，求得DB长，继续放在Rt⊿ABD中，勾股定理求AD。

（3）由线段AD放在圆的本质即为弦，而AB为直径的特点，还可考虑作弦心距利用垂径定理只要求得AD的一半即可求解，而在角平分线的前提条件下结合弦心距产生的直角，自然也就出現三线合一的情况，从而判定出等腰三角形。

具体做法：过O做ON⊥AC于N，过O做OM⊥AD于M并延长与AC交于点Q.在Rt⊿ANO中，由垂径定理、勾股定理可求AN、ON，由三线合一可得AQ=OA，再运用勾股定理求得OQ、AM的长，AD也就轻松得之了。

在圆中角平分线问题的基本模型图1的指引下，整个多方法分享过程给学生带来了一场思维盛宴，每出一种新方法学生都不由自主的欢呼雀跃、鼓掌，我能看到他们脸上流露的发自肺腑的喜悦。此题经过我们师生多维度的分析与探究，已经将初中所学几何知识的极大部分进行了充分运用，并能迁移至各种多变题型中，用实践来检验模型图的强大之处。而对此题还没有使用到模型图1和模型图2的结论，在实际解题的过程中，还和学生共同发现了其影子，原来谈“圆”色变的学生现在对圆竟饶有兴致了。

3   结语

在这个探究过程中我也切实领悟到我们的教学需要更多的研究与思考，我们的题在于精而不在多，我们的讲解在于透而不在繁。在探究的过程中我们师生也在相互促进，在探究的过程中我们也发现了数学的各种趣味性、巧妙性以及延展性，不但与学生共同感受知识的博大精深，也激发我们勇于思考，彼此分享与交流的情感。这种情怀不仅受益于我，更受益于我们的学生。

【参考文献】

[1]蓉城学堂编委会.蓉城学堂 中考总复习点击与突破（作业手册[M].成都：四川大学出版社，2019.