浅谈分数应用题的基本功与解题策略

谭应新

摘 要：小学分数应用题来源于现实生活，有着丰富的生活题材。是小学数学教学的重难点内容，重点是分数与除法和比有直接的联系，学生容易在运用知识解决问题时混清不清。难点是分数应用题在解题时尤其突出的数量与分率的对应关系，必须要求学生懂得找等量关系，或者画图进行分析。因此在解答分数应用题时，审题、研题的基本功是否扎实过关，遇到分析的盲区时能否主动画图寻求突破口直接影响学生的解题效果。在我的教学实践的过程中，也从学生遇到的各种解题困难中积累了一些行之有效的方法，借此文章与广大数学老师交流分享下。

关键词：分数应用题;基本功;策略

一、两个基本功

数学的基本功包括：1、数与代数，即具备数与数之间的四则运算能力，沟通条件与问题的内在联系从而成功解决问题。2、空间与几何，能借助直观图形构建空间平面或立体思维，并能准确运用长度、面积、体积的单位。3、统计与概率，通过图表的语言能力获得解决问题的直接信息。综上所述，分数应用题的解题基本功主要与数与代数这一大环节有关。

（一）、首要任务是教好分数乘法的意义

整数乘法的意义是求几个相同的加数的和的简便运算，教师教学时应以此为切入口，用分数乘整数的具体例子充分调动学生进行讨论交流，从而构建出新知识与已学知识的内在联系。

例如：可以表示3个相加的和是多少，也可以表示的3倍

是多少。而根据乘法交换律原式的积是不变的，即同样可以

理解为3的倍是多少，但习惯上当乘上的倍数不满1时，一般把

“倍”字略去，因此3的倍只说成了3的是多少。这样就顺利地把整数乘法的意义扩展为一个数的几分之几是多少。学生经历这一教学环节成功地探索出分数乘法的意义，既深化巩固了已学过的知识，又探究出新的知识，并真正使分数乘法的意义在他们的认识结构里成功着陆。

（二）、加强分数乘除法应用题的联系与区别

1、通过对比，加深理解。

如教学：例题a：池塘里有12只鸭，鹅的只数是鸭的，池塘里有多少只鹅？

例题b：池塘里有4只鹅，正好是鸭的，池塘里有多少只鸭？

俗语说得好，有对比就有“伤害”，就是通过画模型图直观对比，从而使两道极为相似的题中的已知量和问题之间的内在联系浮出水面，绝大部分学生都会顿时觉悟，茅塞顿开，必然会获得正确的解题效果。

需要强调的是，教师对这类对比教学的指导必须落到实处，因为它是分数应用题的重点，对于学生来说是比较抽象的，不难说会有一部今学生难以理解和掌握，因此，这样审题的指导至关重要，从深入的角度让学生掌握单位“1”是已知的还是未知的，再进一步了解比较量与单位“1”的分数关系，继而形成直观的线段模型图，学生对画图是很感兴趣的，只要尝试到解题的成功感肯定会主动积极地画线段图分析，这样就打开了分析分数应用题的实破口，从而为以后解决更复杂的题目奠定了基础。

在教学简单或较复杂的分数乘除法应用题时，要经常训练学生做一些条件和问题固定，通过变换分率句进行变式解题的题目。

如：为庆祝国庆活动，六年二班的男生购买了18面小红旗，______，女生购买了多少面小红旗？以下有5个分率句的转换，要求学生准确地列式组合。（1）女生购买的数量是男生

的;（2）正好是女生购买数量的;（3）是全班购买总数的

;（4）女生购买的数量比男生多卖;（5）女生购买的数量

比男生少卖。这样就把简单及较复杂的分数乘除法应用题融于一题多变之中。

我给学生的建议是：该类应用题的解题方法是有迹可循的，基本由三大体系组成。一是求数A是数B的几分之几;二是求数A的几分之几是多少;三是已知数A的几分之几是多少，求数A的量。解题的关键是明确分数乘法的意义，分析时遵从单位“1”×分率=对应量，必要时还可以借此等量关系列方程解答。

二、持之以恒，坚持不懈。分数应用题解题四攻略：

（一）主动出击，画图理解题意。

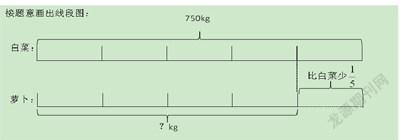
如：菜场运来白菜750kg，运来的萝卜比白菜少，运来萝卜多少千克？

看图分析可列出两个算式：a.750-750×  b.750×（1-

）对于相对简单一些的分数应用题，要花大力气教会学生画线段图，部分学生的语感是很差的，要求他们在未读懂题目的情况下利用线段图分析是相当困难的，我的做法是先给定一个比较稳定的思维建构模式，如果单位“1”对应的数量是己知条件，就得先找出所求问题占单位“1”的对应分率，然后用乘法列式解答。如果单位“1”对应的数量是未知，就从已知条件入手，找与己知量占单位“1”的几分之几，再用列方程或用除法列式解答。

（二）巧用对应分率解分数应用题。

这一解题策略以上已经引申出来了，但如果学生能真正培养出在解题时摸清量率之间的对应关系的能力，则说明运用画线段图分析就已经非常熟练，因此解决分数应用题的核心就是能逻辑合理地把条件、问题之间的关系直观地表达出来，而且不难看出作图能力好的学生的思维能力是特别好的，他们解题时往往是信心十足。

以下举一实例阐明一下找对应分率的步骤和技巧吧！

如：六年级有138个学生，其中有的学生订了《科学画

报》，有的学生订了《智力快车》，这两种读物都订的有多少个学生？

根据“有的学生订了《科学画报》，的学生订了《智力快车》”

可以画出线段图帮助找出问题的对应分率。

从上图可看出两种读物都订的占总人数的+-1=，因

此列式为138×（+-1）=138×=69人

我还经常结合学生的解题经验作分享交流：在分数应用题中，具体的数量对分率有时是直接对应的，有时是间接对应的，转化对应分率的方法是：比单位“1”多时，用“1+几分之儿”，比单位“1”少时用“1-几分之几”。只要正确地锁定“量率对应”，问题就可迎刃而解了。

（三）培养逆向思维。

对于大部分孩子来说，他们的思维顺序都是由先到后的，但对于某些特定的题目就容易把思路带入了死胡同，从而令学生无计可施，甚至陷入绝境。这时候倒不如逆过来想一想进行逆向推理，这样就可能悟出解题的入口，使思路順利打通，收到意想不到的解题效果。

（四）把单位“1”进行合理的转化。

学生解决分数应用题的时候，最头疼的是出现两个或两个以上的分率，说明题中的单位”1“是不唯一的，即各个分率对应的单位“1”是不同的，但其实它们之间是有着密切的内在联系的。那么在解题时以某一个单位”1“为标准的对应量，将其余量的对应分率统一到这个标准量上来计算就可以列式解答。具体范例如下：

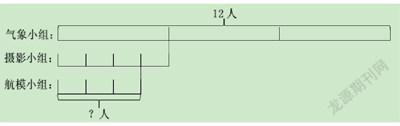
学校气象小组有12人，摄影小组的人数是气象小组的，航

模小组的人数是摄影小组的，航模小组有多少人？（【参考书籍】北师大版数学六年级上册第21页）

我会指导学生先回归到解题的核心，画线段图分析：

从上图中仔细分析就能看出航模小组人数是气象小组人数

的（×），先巧算出这个对应分率，列式为：12×（×）。

总概而论，分数应用题对于全班80%以上的同学都觉得挺困难的，只有循规蹈矩，踏踏实实地教给学生正确的解题方法，结合自身的思维优势制定出合理准确的解题方法。遇到不同的分数问题能灵活运用解题策略，从分数的基本功入手，提高学生的自信心，帮助学生在分析时善于画图理解，从培养学生分数应用题转化为解决生活实际问题的能力才是教材设计的本质内涵。