基于地铁的城市物流配送路径优化

刘亚楠 郑长江 沈金星

摘 要：为了应对日益增长的快递需求，缓解货运车辆加重的城市交通拥堵，提高城市配送效率，本文提出了整合地铁资源进行城市物流配送的构想。本文将从企业和用户的角度出发，考虑地铁与末端地面配送车辆的容量限制，以运输成本、车辆成本和时间成本最小为目标函数建立多目标优化模型，优化地铁列车班次的客户分配和末端地面车辆的路径选择，更加符合实际。然后采用遗传算法对模型进行求解。最后以南京市地铁2、4号线为例，验证了模型和算法的实用性及有效性。结果表明，基于地铁的城市物流配送的总成本远低于单独货车配送，具有较强的应用价值。

关键词：地铁;城市配送;容量限制;多目标

中图分类号：U121

文献标识码： A

随着城市化进程的加速与电子商务的蓬勃发展，城市里各类车辆数目激增，道路交通拥堵现象愈发严重。而城市中有60%的车流是运货的，如果将地面货运转至地下，将大大减少交通压力[1]，有效缓解交通环境和空间资源的矛盾。但是由于地下空间开发目前还处于起步阶段，存在建筑地下基础深浅不同、地下空间受力环境复杂等问题，地下物流系统建设面临成本与技术的双重难题。基于地铁的城市物流配送构想，既能充分利用地铁资源，又能为地下物流系统的成功实施减少阻力。《“十三五”交通领域科技创新专项规划》也提出要开发适于城轨客运空档期专用的智能及经济性载运工具。因此，将地铁引入城市配送将是未来的重要研究方向，具有重要的研究价值。

将公共地铁服务与传统的货车运营相结合，把货物从郊区运送到城市中心，可以有效緩解交通拥堵、延误、环境污染等城市交通问题[2]。国内外许多学者已经从技术上和经济上验证了其可行性。MOTRAGHI等[3]利用 Arean 仿真软件建立模型，用于分析现状评估备选方案并最大限度地利用地铁系统，结果表明利用地铁实现城市货运是可能的。张涵等[4]提出了“云平台+公共交通”的智慧物流整合设计方案，包括以地铁为末端配送主力， 辅助小型运输工具完成配送。刘崇献[5]分析了把北京地铁在晚问和非高峰期用作城市物流系统的必要性和可行性。史毅飞等[6]提出了使地铁兼具载客、物流功能的改造方案，分析了客流低谷、非载客两个时间区间地铁运行模式。彭玫贞等[7]通过地下物流系统与地铁在技术系统结构、网络布局、实施环境与运营等方面均的异同，证明两者之间的协同具有可行性，并具有较大优势。陈梓毓[8]分析了适合地铁配送的货物类型、运载工具、货物流向、区间范围和货物量。

目前国内外对基于地铁的城市物流配送路径优化的研究较少。GHILAS等[9]探讨了利用现有的按预定路线和时间表运营的公共交通车辆运输货物的机会和可行性，提出了一种适用于带时间窗和预定线路的收送货问题的自适应大邻域搜索算法。杨浩雄等[10]从利用轨道交通配送鲜活农产品出发，研究了配送模式的流程、配送线路规划原则及基础设施的建设与改造问题。周芳汀等[11-12]以货物平均送达时间最小为目标函数构建模型，以优化配送中心与地铁出站点的选择和末端地面配送路径，其后又以配送成本最小化为目标，优化了地铁列车的客户分配及末端地面配送路径。

虽然已有少量文献对基于地铁配送的城市物流路径优化进行了研究，但其研究对象仅为单条线路，没有考虑受客流影响的地铁列车班次剩余能力情况，研究目标多从物流企业的角度考虑运输成本最小化，忽视了客户利益。因此，本文将从企业和用户的角度出发，考虑地铁与末端地面配送车辆的容量限制，以运输成本、车辆成本和时间成本最小为目标函数建立多目标优化模型。在算例中采用遗传算法求解，优化地铁列车班次的客户分配和末端地面车辆的路径选择。

1 问题描述与建模

1.1 问题描述

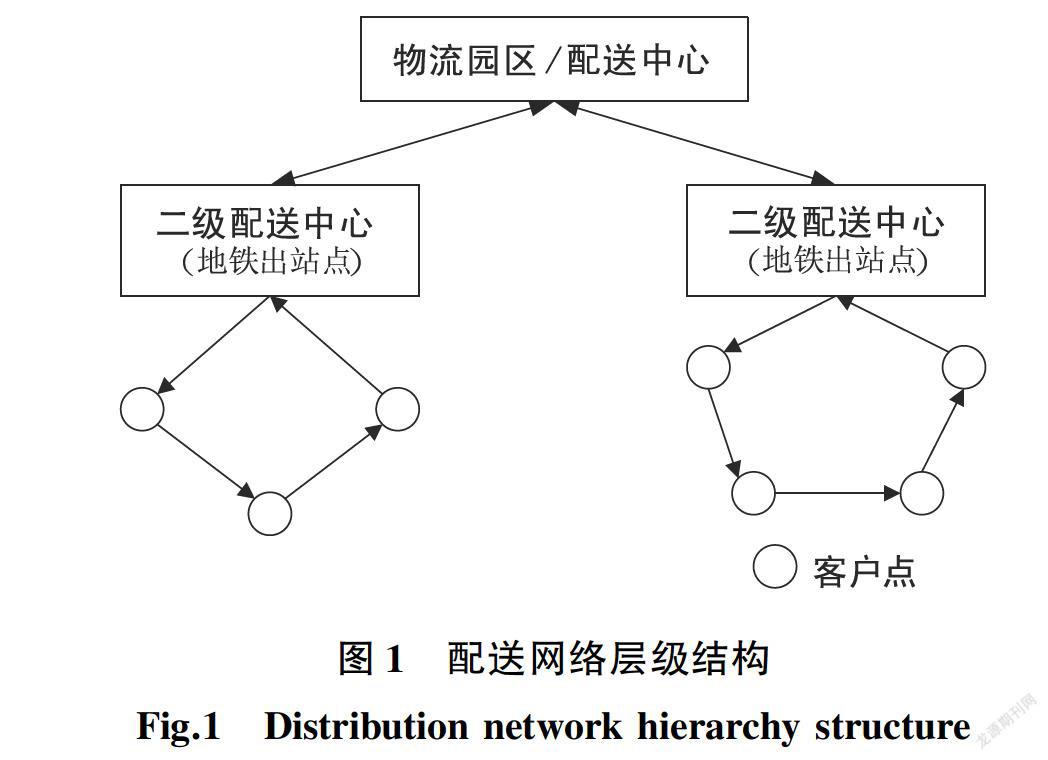
配送中心的货物分拣后由货车运往指定的地铁进站点，经过地铁运输至出站点，再由末端的地面配送车辆运输给客户，如图1所示。配送中心可以就近选择某几条地铁线路作为配送线路，其中地铁线路剩余能力已知。进站点到出站点的距离和时间已知。客户的收货需求和坐标位置已知。配送完成后地面配送车辆（包括从配送中心出发的货车及从出站点出发的末端配送车辆）需要返回起始点，地铁列车不需要。货物一般为中小型包裹和低密度高附加值货物，需要尽快送达。

1.2 模型假设

模型基本假设如下：

（1）地铁、货车与末端配送车辆的运输成本只与货物重量与运输距离有关，不考虑其它因素的影响。

（2）配送中心对应有固定的地铁进站点。

（3）进站点到出站点的容量限制是固定的，暂时不考虑其随客流变化情况。

（4）在考虑配送网络上地铁的容量限制下，地铁线路运输货物不会影响乘客服务质量。

（5）不同的运输方式转运时，会有一定的时间损耗。

1.3 模型建立

1.3.1 货物运输成本

由图1的配送网络层级结构可以看出，货物运输成本应当包含三部分：配送中心至地铁进站点的地面运输部分，地铁进站点至出站点的地铁运输部分以及地铁出站点至用户的末端地面运输部分。在建立模型时，考虑到假设了物流园有固定的进站点，因此，当已知进站点时，配送中心到该进站点的距离、时间等成本亦可得到。故可将运输成本的前两部分合并，建立的货物运输成本模型如下：

C1=∑d∈VD∑k∈VK∑j∈VC∑r∈VRcodkqjxjrdk+∑i∈VK∪VC∑j∈VC∑v∈VVcijqjyjvij

其中，C1为货物运输总成本，VD为进站点d的集合，VK为出站点k的集合，VC为客户j的集合，末端地面配送节点i∈VK∪VC，VR为地铁班次r的集合， VV为路面配送车辆v的集合;codk为从配送中心经过进站点d到出站点k的单位货物运输成本，qj为第j个客户的货物需求量，cij为末端配送从节点i到j的单位货物运输成本，决策变量xjrdk表示客户j的货物由配送中心经过进站点d到出站点k通过列车班次r配送时取值为1，否则为0;决策变量yjvkj表示客户j的货物从出站点k到客户j由车辆v配送时取值为1，否则为0。

1.3.2 车辆成本

在城市物流配送中，应该尽量提高配送车辆的满载率，减少车辆的使用。这样不仅能够降低成本，也是缓解交通拥堵的关键。因此车辆成本目标函数如下：

C2=crNr+cvNv

其中，C2为车辆总成本，Cr为每班次地铁列车车辆成本，Cv为单辆末端地面配送车辆成本，Nr为所需地铁列车班次数，Nv为所需末端配送车辆数。

1.3.3 时间成本

时间成本的目标函数一般为最大服务时间最小、平均服务时间最小等。本文选择使用平均配送时间最小为目标函数。与运输成本一样，配送中心到地铁进站点的时间成本与进站点到出站点的时间成本也可以合并在一起计算。由此得到如下目标函数：

T=∑d∈VD∑k∈VK∑j∈VC∑r∈VRtodkxjrdk+∑i∈VK∪VC∑j∈VC∑v∈VVtijyjvijNC

其中，T为货物平均送达时间，todk为从配送中心经过进站点d到出站点k的单位货物运输成本，tij为从节点i到节点j的单位货物成本，NC为客户的数量。上述公式第一部分表示配送中心到达出站点的时间之和，第二部分表示出站点到达客户的是时间之和，两者相加即为所有货物配送的总时间，除以客户总数量即为货物的平均送达时间。

因此，统一量纲后，模型目标函数的数学形式可以表述如下：

minZ=C1+C2+T=∑d∈VD∑k∈VK∑j∈VC∑r∈VR（codkqj+todk/NC）xjrdk+∑i∈VK∪VC∑j∈VC∑v∈VV（cijqj+tij/NC）yjvij+crNr+cvNv

1.4 约束条件

∑v∈VVyjvkjSymbolcB@

∑d∈VD∑r∈VRxjrdk，k∈VK;r∈VR

∑d∈VD∑k∈VK∑j∈VCqjxjrdkSymbolcB@

Qr，r∈VR

∑i∈VK∪VC∑j∈VCqjyjvijSymbolcB@

Qv，v∈VV

∑j∈VCyjvij=∑j∈VCyjvjiSymbolcB@

1，i∈VK∪VC;v∈VV

∑d∈VD∑k∈VK∑r∈VRxjrdk=1，j∈VC

∑i∈VK∪VC∑v∈VVyjvij=1，j∈VC

xjrdk∈{0，1}，d∈VD;k∈VK;j∈VC;r∈VR

yjvkj∈{0，1}，k∈VK;j∈VC;v∈VV

其中，為Qr为地铁r的最大容量，Qv为末端配送车辆v的最大容量。式（5）表示若客户j的货物运输使用了d到k地铁线路，那么地面配送车辆应该在k处转运。式（6）、（7）分别为地铁r的容量限制和末端配送车辆v的容量限制。公式（8）确保末端地面配送车辆从出站点出发，最终回到出站点。公式（9）（10）为决策变量约束，分别表示客户j的货物必须且只能由一列地铁班次和一辆地面配送车来提供服务。式（11）、（12）为决策变量的0-1约束。

2 模型求解

遗传算法是一种进化算法，其基本原理是仿效生物界汇总的“物竞天择、适者生存”的演化法则。它通过把问题参数编码为染色体，再利用迭代的方式尽心选择交叉以及变异等运算来交换种群中染色体信息，最终生成符合优化目标的染色体[13]。

Step0：编码。由于真实值编码可以将个体中性状优良的基因片断遗传到下一代，使该片断在子代中中仍然保持优良，因此，本文采用自然数编码方式。

Step1：初始种群的产生。将客户随机分配各个出站点，如分配给某个出站点的需求点数量N1，随机生成该组需求点的1个排列，计算需在改排列中插入进站点和配送中心的数量N2=N1-1，并将N2个进站点和配送中心随机插入排列中，生成新的排列[14]。对其它出站点重复上述过程，最终将得到的排列顺次组合，得到一个初始种群。

Step2：对各染色体编码进行可行性检验。若某染色体编码存在一条配送路径上的货物超过配送车辆的最大容量，则重新随机生成新染色体编码替换该染色体编码，直至所有染色体编码均通过容量限制要求。

Step3：计算适应值。计算此时种群中的各个染色体i的适应值Fi，评估个体的优劣性。

Step4：选择操作。基于赌轮选择法，计算选择概率Pi。从种群中随机产生一些染色体，产生并组成新的种群。

Step5：交叉操作。采用部分映射杂交，即确定交叉操作的父代，将父代样本两两分组，交叉后同一个体不重复的编号保留，有冲突的数字编号利用中间段的对应关系进行映射。

Step6：变异操作。变异策略选择随机选取2个点，将其对换位置。

Step7：终止准则。采用最大进化代数终止准则，即如果算法尚未达到则返回Step3继续进行计算。

3 实例分析

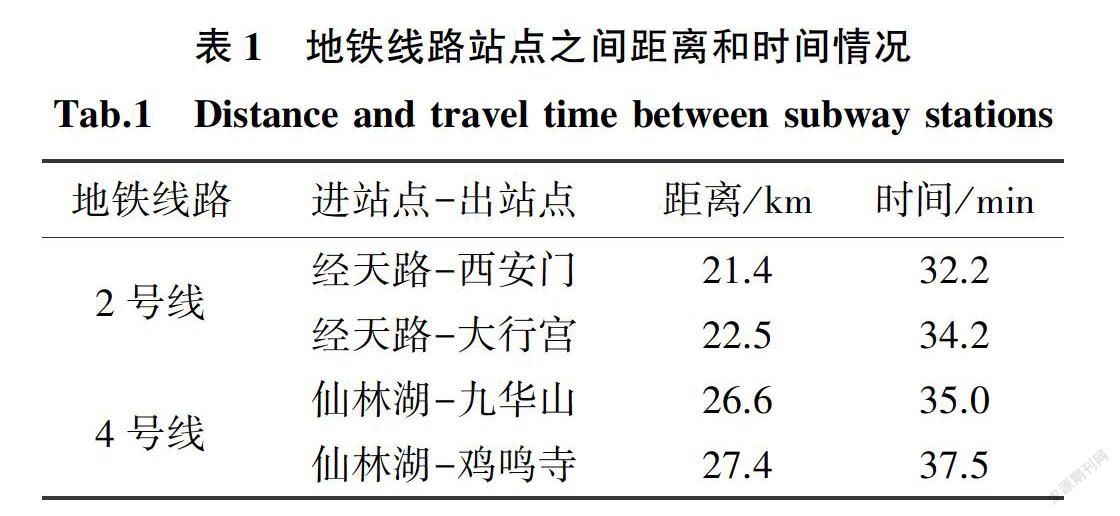
某企业需要经过南京三志物流园向市区16个客户运送货物，选取地铁2、4号线作为配送线路，仙林湖站和经天路站为进站点，西安门站、大行宫站、九华山站和鸡鸣寺站作为出站点。物流园到地铁进站点的装运时间分别为20 min（仙林湖站）、24 min（经天路站）。根据客流数据，假设地铁2、4号线可用于货物运输的容量限制分别为60、100。末端配送车辆的速度取10 km/h，容量限制为40。为方便计算，假设客户需求均为10，地理位置服从均匀分布，可通过百度地图获取坐标及其之间距离。物流园区到进站点运输、地铁运输、末端配送以及货车单独配送的单位货物单位距离运输成本分别为0.4、0.05、0.2、0.4。货车、地铁、末端配送车辆成本分别取10、2、3。转运时间和客户服务时间分别取5 min、1 min。

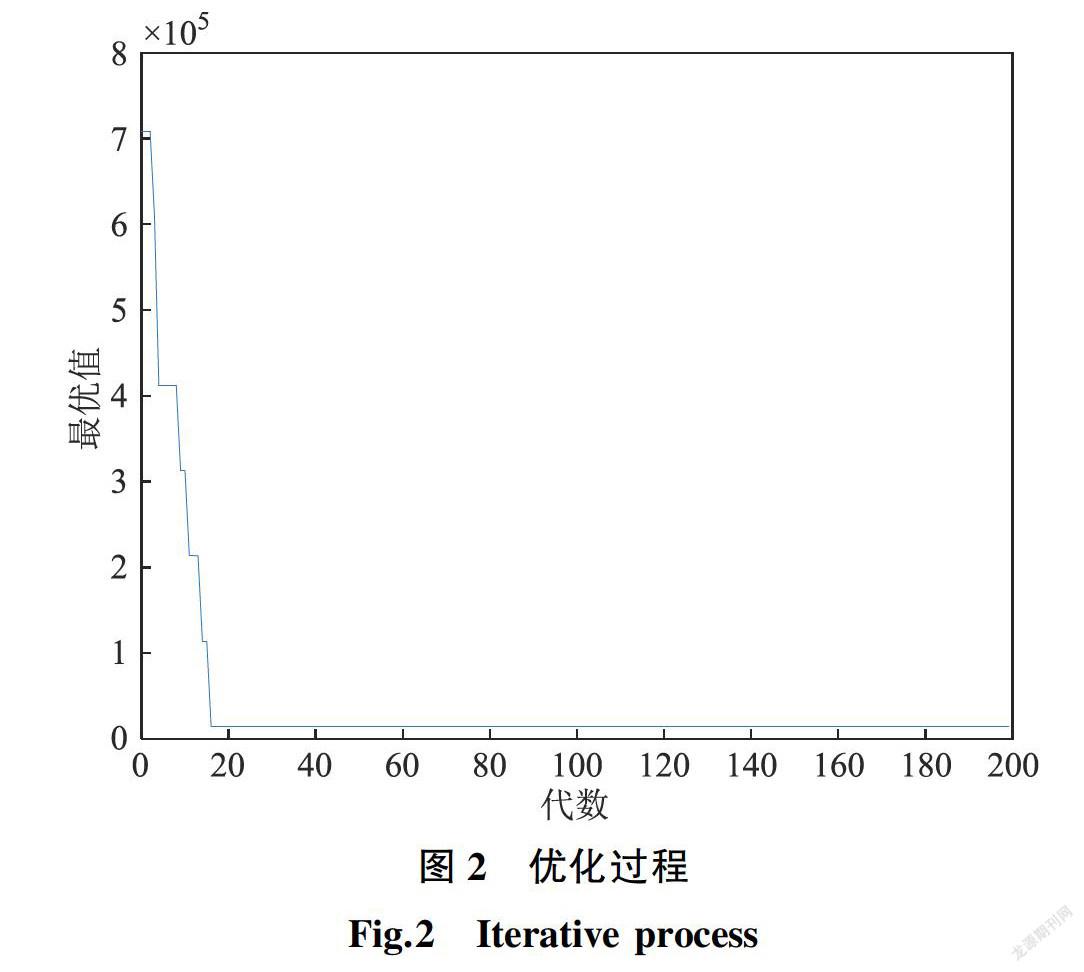
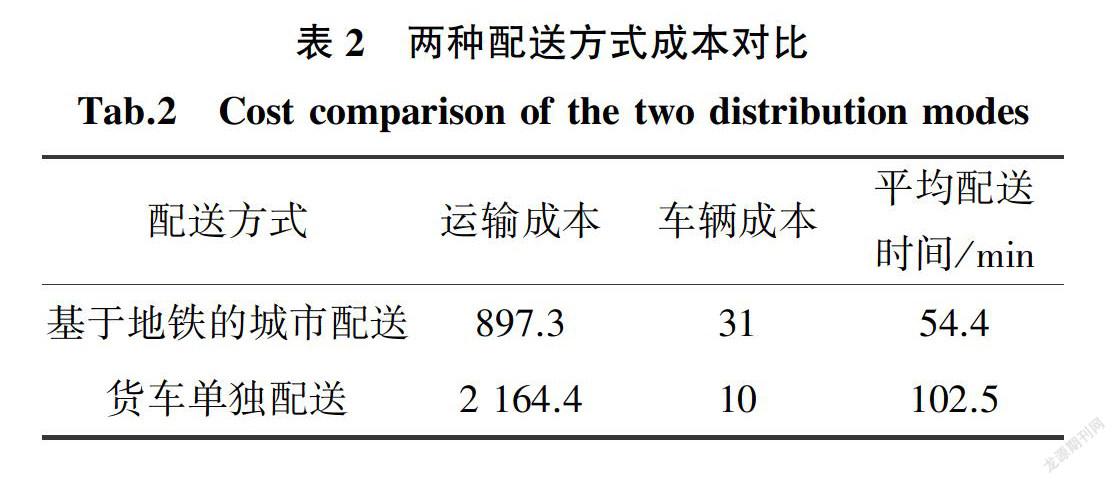
在matlab中编码，种群规模取100，交叉概率取0.9，变异概率取0.05，代沟取0.9，用O表示物流园区，A表示仙林湖，B表示经天路，c表示鸡鸣寺，d表示九华山，e表示大行宫，f表示西安门。基于地铁的配送路径优化结果为：O→A→c→1→2→6→5→c，O→A→d→13→14→10→9→d，O→B→e→8→4 →3→7→e，O→B→f→12→11→15→16→f。2号线需要2列列车班次，4号线需要1列列车班次。对货车单独配送路径优化结果为：O→15→16→12→8→4→3→7 →6→2→1→5→9→13→14→10→11→O。两种配送方式的成本如下表：

由上表数据可知，基于地铁的城市配送，配送车辆在完成配送时所需的平均配送时间为54.4 min，运输成本为897.3。由于在配送过程中，存在车辆转运情况，故所需的车辆成本高于货车单独配送。但是，车辆成本增加了21，运输成本却减少了1267.1，平均配送时间缩短了48.1 min。

4 结论

本文构建了基于地铁的城市物流配送路径优化模型，利用遗传算法求解模型。考虑了地铁、末端配送车辆的容量限制与多条地铁线路共同配送的情况，得到的结果更加符合实际。

（1）基于南京地铁2、4号线的实例分析，证明了模型可以反映不同车辆间的转运关系，得到的配送方案优化了地铁列车的客户分配和末端地面配送车辆的路径选择，有利于道路与地铁配送网络整体能力的发挥。

（2）优化模型与单独货车配送的配送方案相比，虽然车辆成本增加了21，运输成本却减少了1267.1，平均配送时间也缩短了48.1 min，有效减少了配送总成本。

研究成果可以为城市配送企业提供决策支持。根据客流情况考虑地铁在不同时段、路段的动态剩余能力是本文今后的研究方向。

参考文献：

[1]陈小坚， 李海华.  拓展建设“节约型城市”的新思路，合理开发利用城市地下空间：访中国工程院院士钱七虎先生[J]. 现代城市研究， 2005， 20（6）：14-16.

[2]KIKUTA J ， ITO T ， TOMIYAMA I ， et al. New subway￣integrated city logistics szystem[J]. Procedia-Social and Behavioral Sciences， 2012， 39：476-489.

[3]MOTRAGHI A ， MARINOV M V . Analysis of urban freight by rail using event based simulation [J]. Simulation Modelling Practice and Theory. 2012， 25：73-89.

[4]张涵， 孙伟彤.  基于“云平台+公共交通”的城市智慧物流末端配送体系构建设想[J]. 中国战略新兴产业， 2017（20）：84.

[5]刘崇献.  北京地铁晚间和非高峰期用作城市物流系统探讨[J]. 城市发展研究， 2011， 18（06）： 122-124.

[6]史毅飞.  关于地铁兼具载客、物流功能的可行性分析[J]. 物流技术， 2014， 33（1）：197-199.

[7]彭玫贞， 董建军， 任睿， 等.  城市地下物流系统与地铁的协同运行探析[J/OL]. 解放军理工大学学报（自然科学版）， 2017[2019-10-29].http：//kes. cnki.net/kcms/detail/32.1430.DOI：20170926.1428.008.html.

[8]陈梓毓. 南京地铁开展城市配送的可行性研究[D]. 南京：南京大学， 2017.

[9]GHILAS V， DEMIR E， VAN WOENSEL T. An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows and scheduled lines[J]. Computers & Operations Research， 2016， 72：12-30.

[10]楊浩雄， 殷娟娟.  利用城市轨道交通配送鲜活农产品的研究[J]. 黑龙江农业科学， 2012， （8）：114-117.

[11]周芳汀， 周国华， 张锦. 基于地铁开展城市配送的选点-路径问题[J]. 控制与决策， 2018， 33（7）：1247-1254.

[12]周芳汀， 张锦， 周国华. 带时间窗的地铁配送网络路径优化问题[J]. 交通运输系统工程与信息， 2018， 18（05）：88-94.

[13]郁磊， 史峰， 王辉， 等.  Matlab智能算法30个案例分析[M]. 2 版， 北京：北京航空航天大学出版社， 2015：1-2.

[14]杨忠振， 穆雪， 朱晓聪. 交通流变化下的多配送中心-多需求点配送网络优化模型[J]. 交通运输工程学报， 2015， 15（1）：100-107.

（责任编辑：于慧梅）

Optimization of Urban Logistics Distribution Routing Based on Subway

LIU Yanan1， ZHENG Changjiang1*， SHEN Jinxing

（College of Civil and Transportation Engineering， Hohai University， Nanjing 210098，China）

Abstract：

In order to cope with the increasing demand for express delivery， alleviate the urban traffic congestion caused by freight vehicles， and improve the efficiency of urban distribution， this paper puts forward the idea of integrating subway resources for urban logistics distribution. Considering the capacity limitation of subway and terminal ground distribution vehicles， it established a multi￣objective optimization model from the perspective of enterprises and users with the objective function of transportation cost， vehicle cost and time cost， to optimize customer assignments for subway trains and routing selection for terminal ground distribution vehicles. The establishment of this model is more in line with the actual situation. Then the genetic algorithm is used to solve the model. Finally， taking Nanjing Metro Lines 2 and 4 as an example， the practicability and effectiveness of the model and algorithm are verified. The results show that the total cost of urban logistics distribution based on subway is much lower than that of individual trucks， which has strong application value.

Key words：

subway; urban distribution： capacity limitation; multi￣objective