混凝土棱柱面网壳的弹性稳定分析

唐攒辉 张华刚 魏威 张鑫 吴琴

摘 要：混凝土棱柱面网壳是由曲面切割成一系列平面后，再将每块平面网格化成密肋平板并在脊线处汇交形成的一种新型混凝土网壳结构，为探讨其稳定性能，并了解结构失稳模态和失稳荷载，以及矢跨比、屋面板厚度和密肋梁、脊线梁、主拱及边梁刚度等因素对结构临界荷载的影响，本文采用有限元法进行结构弹性稳定的参数化分析。计算结果表明：结构的低阶失稳模态与柱面拱壳具有较大的整体相似性，模态最大位移主要出现在密肋平板上，设置主拱和脊线有利于提高结构刚度，弹性失稳临界荷载远大于结构的使用荷载;增大矢跨比能有效提高结构的整体刚度，建议结构的矢跨比不宜低于1/6;屋面板厚度可取网格短边尺寸的1/30;增加密肋梁的截面高度有利于提高结构的弹性稳定承载力，密肋梁截面高度可按结构跨度的1/100～1/80确定;主拱是屋盖的主要受力结构，其截面高度可按屋盖跨度的1/70～1/50确定;脊线梁和边梁刚度的改变几乎不会对结构的临界荷载产生影响。

关键词：混凝土棱柱面网壳;弹性稳定;临界荷载;失稳模态;有限元法

中图分类号：TU313.1

文献标识码： A

混凝土薄壳结构受力合理、形式丰富、自重较轻，从上世纪30年代开始被应用于空间结构以来[1]，至今在现代工程中仍有应用，2007年建成的华南理工大学体育馆采用了预应力混凝土双曲抛物面薄壳结构[2]，2011年建成的银川火车站东站房主入口大厅屋盖为混凝土三连跨拱壳结构[3]，2015年建成的中煤建安集团研发中心展览馆采用了气膜钢筋混凝土椭球形薄壳结构[4]。

为解决混凝土薄壳支模复杂的问题[5]，近年來出现了若干新型混凝土壳体结构。TENG等[6]提出的钢-混凝土组合薄壳结构由带肋钢壳和混凝土薄壳共同组成，有效解决混凝土浇筑的模板问题;常玉珍等[7]在混凝土带肋薄壳基础上提出的对肋外包U型钢组合结构，壳板预制时可加快施工速度;孔煜等[8]开展了混合型扁网壳研究，在壳体薄膜内力为主的区域采用混凝土带肋壳，弯曲内力为主的区域则为钢-混凝土组合网壳，充分利用了扁壳的内力分区特点;董石麟等[9]提出的单层钢网壳-混凝土带肋壳组合结构，可将单层钢网壳作为混凝土预制壳板安装时的支架，且施工时钢网壳的承载力及稳定验算至关重要[10];将织物纤维与混凝土结合使用，也有学者在开展纤维混凝土壳体结构的研究[11]。上述工作有效推动了现代混凝土壳体结构的发展。

将大跨度折板壳网格化，张华刚等[12]提出的混凝土折板网壳结构，可以理解为是由密肋平板汇交构成的新型混凝土空间结构，有效降低了网壳施工的支模难度，结构具有较好的技术经济指标[13]。其中混凝土棱柱面网壳是典型的单向传力网壳，当前对其力学性能的研究主要在静力性能[14]和动力特性[15]等方面，由于结构的密肋梁截面尺寸较小，且施工时难免存在初始缺陷，将使稳定问题有可能会成为结构应用的控制条件，而弹性稳定是采用一致缺陷模态法分析结构几何非线性稳定的基础[16]，因此本文基于有限元基本理论对这种网壳结构作弹性稳定的参数化分析，以期为这种结构的工程应用和几何非线性分析提供参考。

1 弹性稳定计算原理

考虑轴向力对结构弯曲变形的影响，由势能驻值原理可得结构的平衡方程为[17]

（[KE]-[KG]）{Δ}={F}。（1）

式中：[KE]为结构弹性刚度矩阵;[KG]为结构几何刚度矩阵，包含单元轴力的影响;{Δ}为节点位移向量;{F}为节点荷载向量。

结构在稳定平衡状态下，势能的二阶变分应为零，即有

（[KE]-[KG]）{δΔ}={0}。（2）

式（2）对任意位移向量均成立，则有

[KE]-[KG]=0。（3）

[KG]中的轴力P为待求量。为了求得失稳模态和失稳荷载，任意假设一组荷载{P0}后，与其对应的几何刚度矩阵为[K0G]，假定失稳荷载为λ{P0}，则当结构失稳时有

[KG]-λ[K0G]=0。（4）

由式（4）解出各阶特征值λi后，即可得失稳模态{Δi}和对应失稳荷载λi{P0}。

2 结构形式及有限元模型

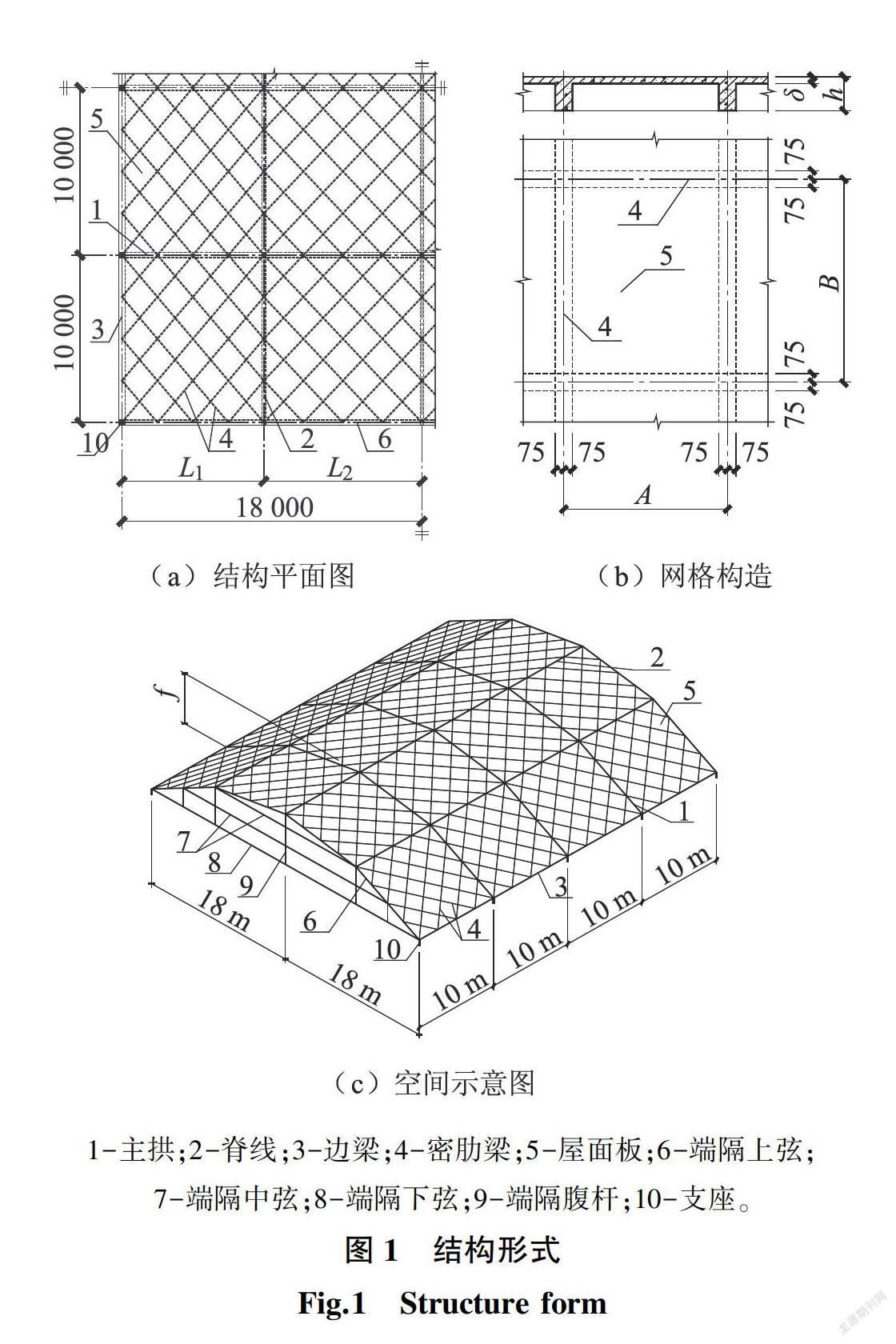
文献[14]的分析表明，混凝土棱柱面网壳采用正交正放网格时，纵向脊线相当于系杆，当边梁的约束刚度又很强时，荷载主要沿拱向传递，致使密肋平板的内力分布极不均匀，因此本文的密肋平板采用斜放网格，结构形式如图1所示，棱柱面由圆柱面等分后用弦平面代替圆弧面得到。通常情况下，由主拱和脊线支承的整块密肋平板很难做到边长相等，因此密肋平板的网格为斜交网格，其构造如图1（b）所示。这样可通过斜放网格传递部分荷载至纵向脊线上，以发挥纵向脊线的承载能力。

本文全部算例的结构跨度均为36 m，纵向长度为40 m，矢高为f;将支承密肋平板的主拱和脊线均划分为4格，密肋平板的网格边长分别为A和B，并将随矢高的改变而改变。文献[14]的分析还表明，端隔对结构受力性能的影响较小，因此本文全部算例的端隔均采用空腹桁架，如图1（c）所示;构件截面尺寸：上弦及下弦为0.3 m×0.5 m、中弦及腹杆为0.3 m×0.3 m;结构其余构件的截面宽度：密肋梁取0.15 m，脊线梁取0.2 m，主拱取0.3 m，边梁取0.4 m。

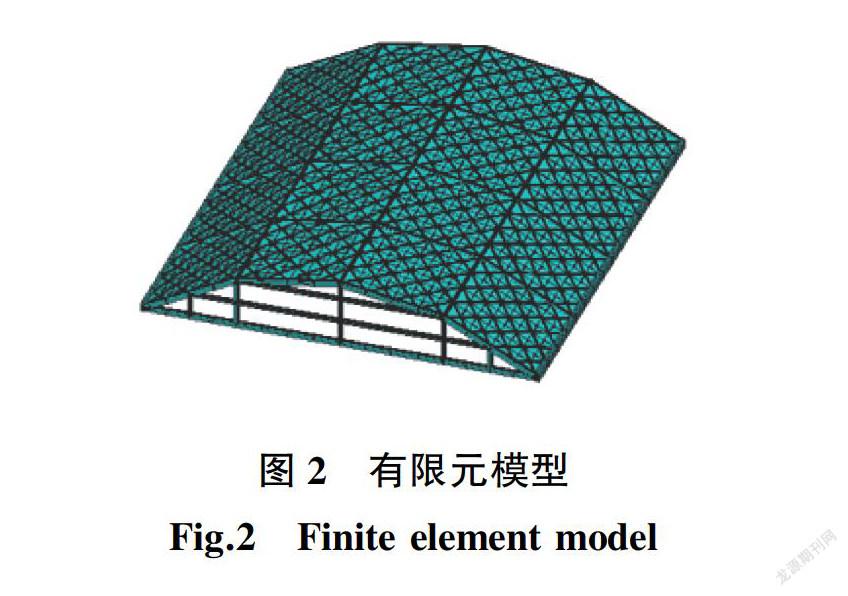
有限元分析时，屋面板采用空间壳单元，其他构件均采用空间梁单元，壳单元的中面与梁单元的中性层重合;边梁按间距10 m作固支点约束;单位均布荷载施加在壳单元上;材料为C30混凝土，弹性模量Ec=3×104  N/mm2、泊松比v=0.2。有限元模型如图2所示。

3 弹性失稳模态及失稳荷载

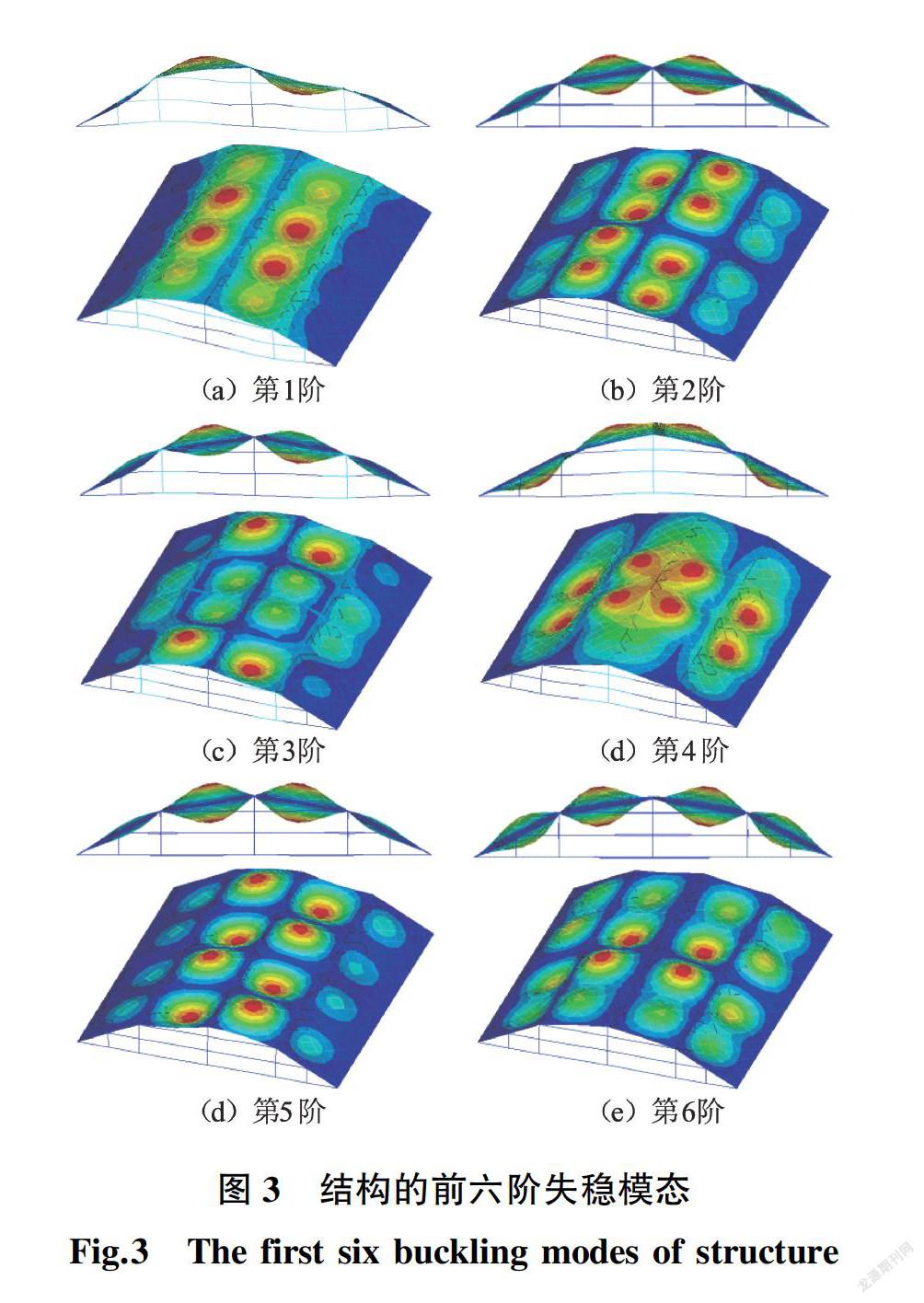
取矢高f=6.0 m作为本文的基本算例，且构件截面高度：密肋梁0.2 m、脊线梁0.45 m、主拱0.5 m、边梁0.8 m，屋面板厚度为60 mm。结构的弹性失稳模态如图3所示，失稳荷载见表1。

可见，结构的低阶失稳模态与柱面拱壳具有较大的整体相似性，但模态最大位移主要出现在密肋平板上，因此设置主拱和脊线是有利于提高结构整体刚度的。前六阶失稳模态均关于结构的对称轴正对称或反对称，其中一阶模态横向关于顶脊线反对称，纵向关于中间主拱半波正对称;二阶模态关于结构对称轴反对称;三阶模态既关于顶脊线反对称，又关于中间主拱正对称;四阶模态关于顶脊线全波正对称、关于中间主拱正对称;五阶模态关于顶脊线半波反对称、关于中间主拱全波反对称;六阶模态关于顶脊线正对称、关于中间主拱反对称。

对于考虑保温隔热的、刚柔性结合防水的屋面，屋盖建筑构造产生的恒载略为3.2 kN/m2，可见结构的弹性失稳临界荷载是远大于使用荷载的。

4 临界荷载的参数化分析

在基本算例基础上，通过改变结构的单参数进行弹性稳定的参数化分析，以了解矢跨比、屋面板厚度及密肋梁、脊线梁、主拱和边梁刚度对结构弹性失稳临界荷载的影响，其中构件刚度通过改变其截面高度来实现。

4.1 矢跨比对临界荷载的影响

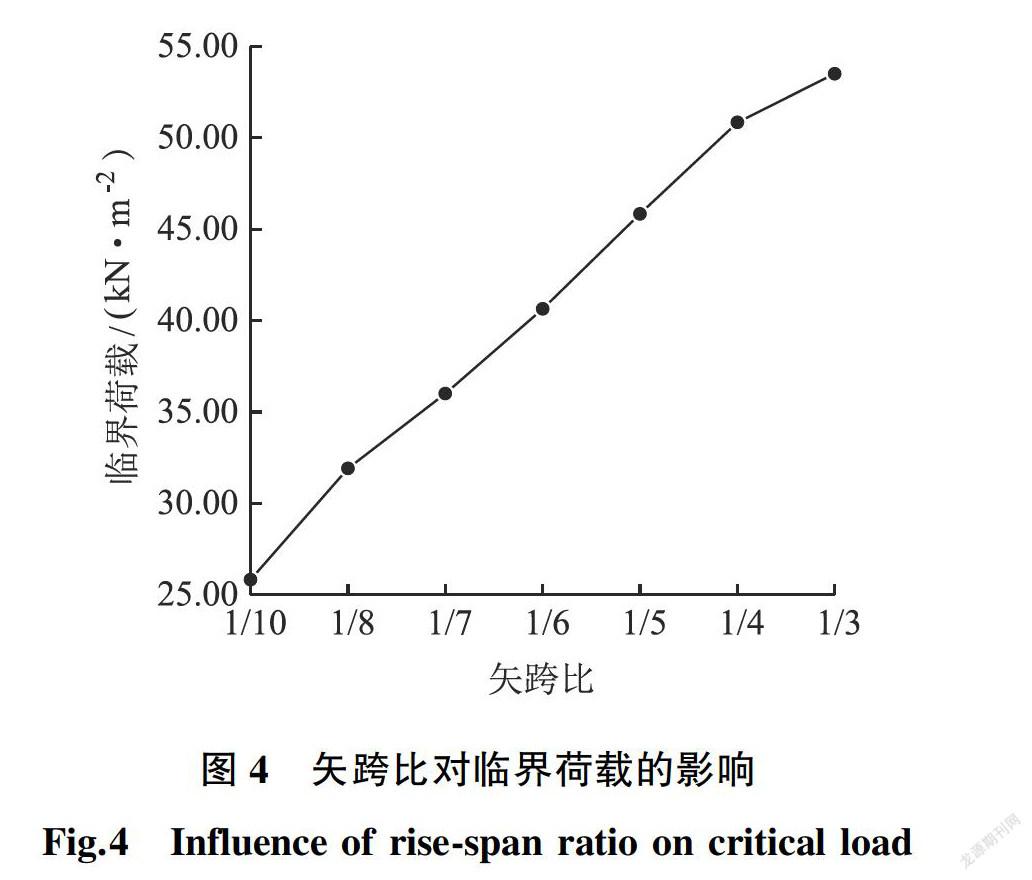
仅改变矢跨比f/L共分析7个算例，矢跨比分别取1/10，1/8，1/7，1/6，1/5，1/4和1/3。临界荷载随矢跨比的变化情况如图4所示。

可见，结构的临界荷载随矢跨比的增大而增大，当矢跨比为1/10时，临界荷载为25.82 kN/m2;当矢跨比为1/3时，临界荷载为53.50 kN/m2，增大了107.2%，在矢跨比为1/7～1/4时，临界荷载随矢跨比的增加近似呈线性增长，矢跨比越大，结构的整体刚度越大，一般不主张结构为浅拱，因此建议这种结构的矢跨比不宜低于1/6。

4.2 屋面板厚度对临界荷载的影响

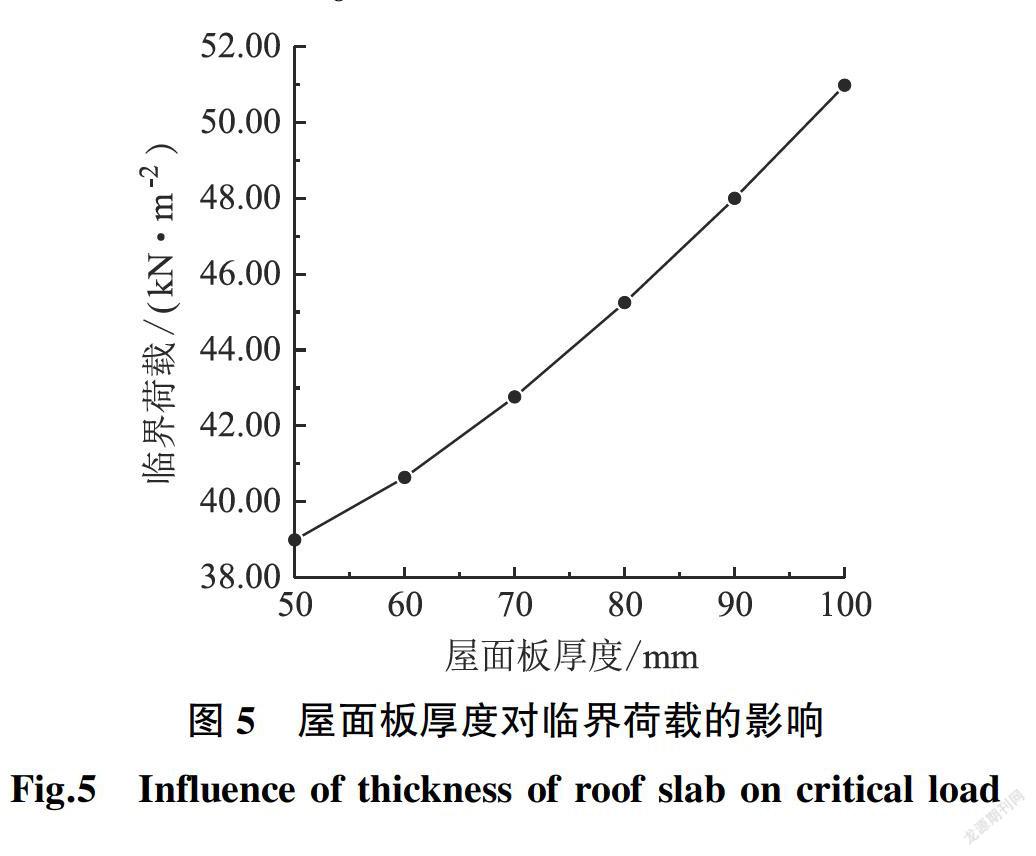
取屋面板厚度为50～100 mm共计算了6个算例，屋面板的厚度级差为10 mm，临界荷载的计算结果如图5所示。

当屋面板厚度为50 mm（约为板跨的1/35）时，临界荷载为38.99 kN/m2;当屋面板厚度为100 mm（约为板跨的1/17）时，临界荷载为50.98 kN/m2，提高了约30.8%。虽然提高板厚可以增加结构的弹性稳定临界荷载，但结合文献[14]的分析，建议屋面板厚度可按网格短边尺寸的1/30取值。

4.3 密肋梁刚度对临界荷载的影响

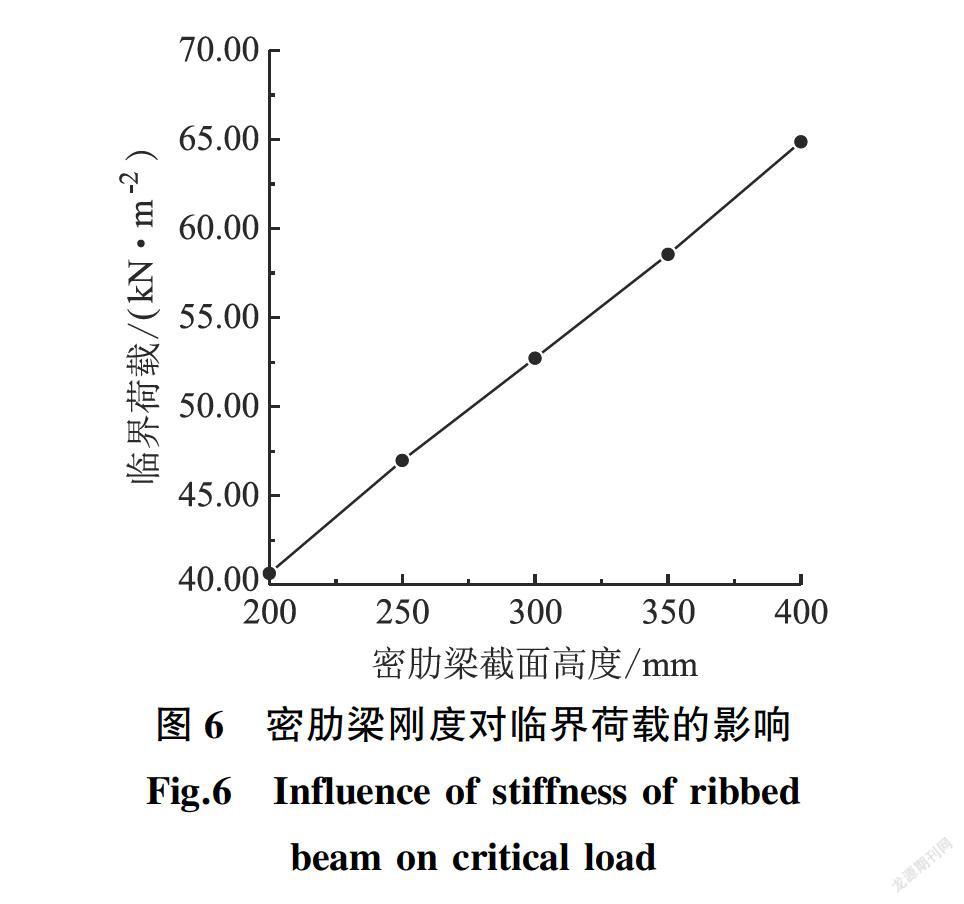
在基本算例基础上，仅改变密肋梁的截面高度共分析5个算例，密肋梁截面高度分别为0.20 m、025 m、0.30 m、0.35 m和0.40 m。弹性稳定临界荷载随密肋梁截面高度变化的结果如图6所示。

弹性稳定临界荷载随密肋梁截面高度的增大近似呈线性增大，当密肋梁截面高度为0.20 m时，相当于屋盖跨度的1/180，临界荷载为40.64 kN/m2;当其截面高度为0.40 m时，约为屋盖跨度的1/90，临界荷载为64.86 kN/m2，增大了59.6%。因此，增大密肋梁刚度有利于提高结构整体刚度并进而提高其弹性稳定性能。结构实际应用时，密肋梁的截面高度可取结构跨度的1/100～1/80。

4.4 脊线梁刚度对临界荷载的影响

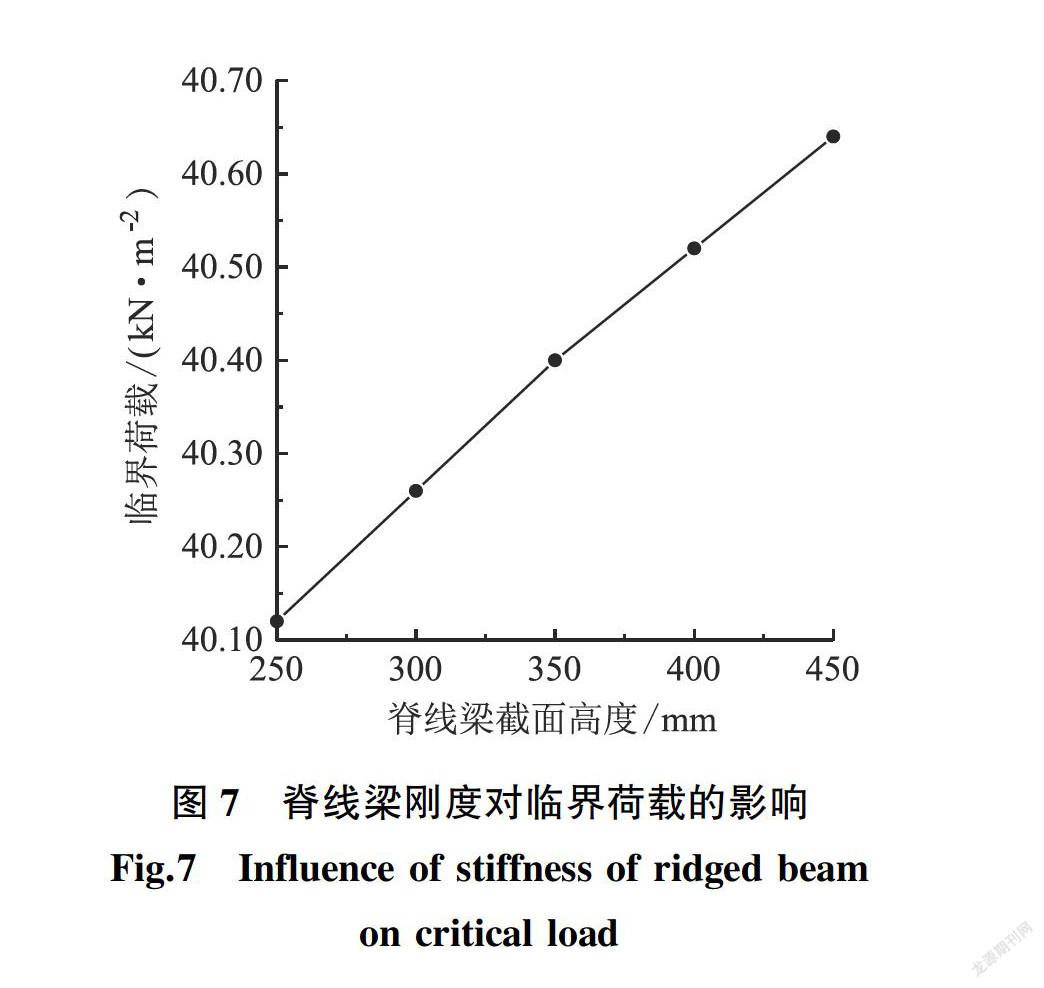
仅调整脊线梁截面高度共计算5个算例，脊线梁截面高度由0.25 m渐变至0.45 m，级差为50 mm，临界荷载随脊线梁截面高度的变化结果如图7所示。

当脊线梁截面高度为0.25 m时，弹性稳定临界荷载为40.12 kN/m2，而脊线梁截面高度为0.45 m时，临界荷载为40.64 kN/m2，仅增大1.3%。

可见，脊线梁刚度的改变对结构弹性稳定的临界荷载几乎没有影响，原因在于密肋平板的斜放网格并未本质改变结构单向传力的性质。

4.5 主拱刚度对临界荷载的影响

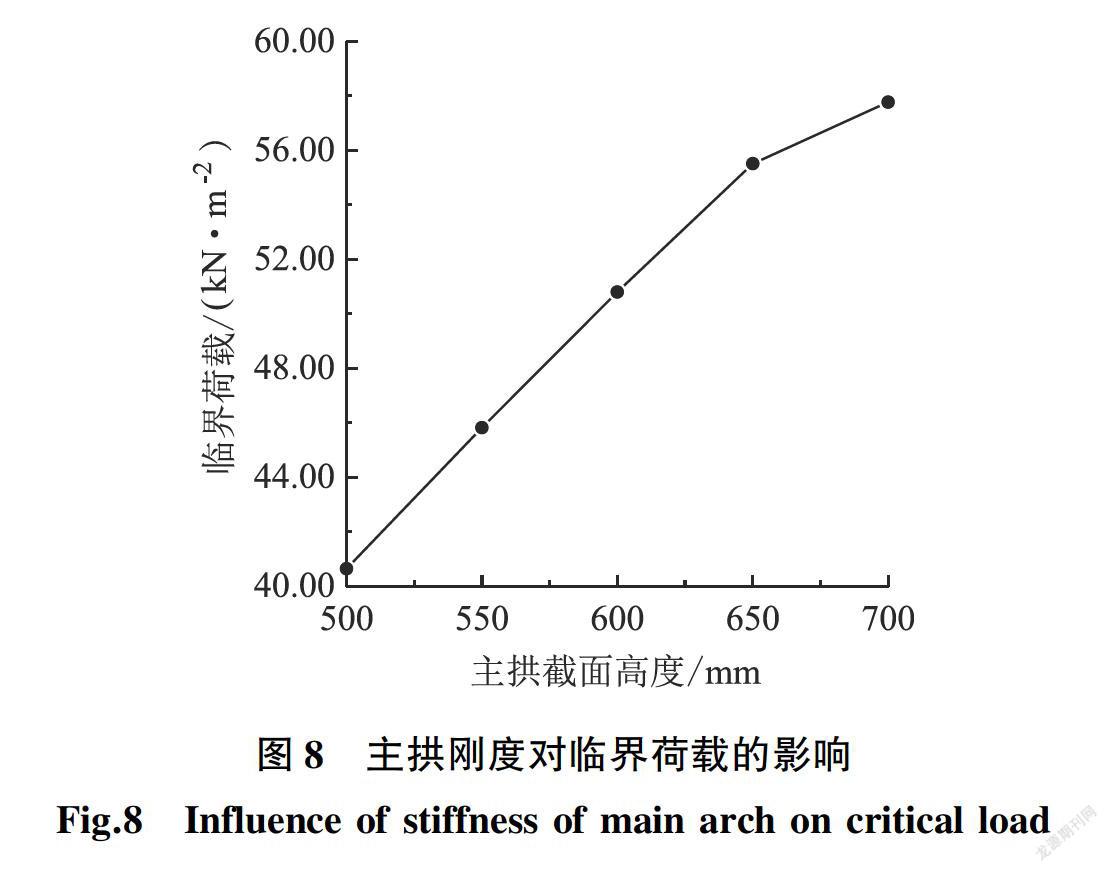
仅改变主拱的截面高度共分析5个算例，主拱截面的高度由0.50 m渐变至0.70 m，级差为50 mm。临界荷载随主拱截面高度的变化情况如图8所示。

可见，临界荷载随主拱截面的高度增大而增大，主拱截面高度为0.5 m时，约为屋盖跨度的1/72，临界荷载为40.64 kN/m2;当主拱截面高度为0.7 m时，约为屋盖跨度的1/51，临界荷载为57.77 kN/m2，增大了42.2%。由于主拱是网壳的主要受力结构，增大主拱的刚度能有效提高结构抵抗弹性失稳的能力。结合静力分析结果，建议主拱的截面高度可按屋盖跨度的1/70～1/50取值。

4.6 边梁刚度对临界荷载的影响

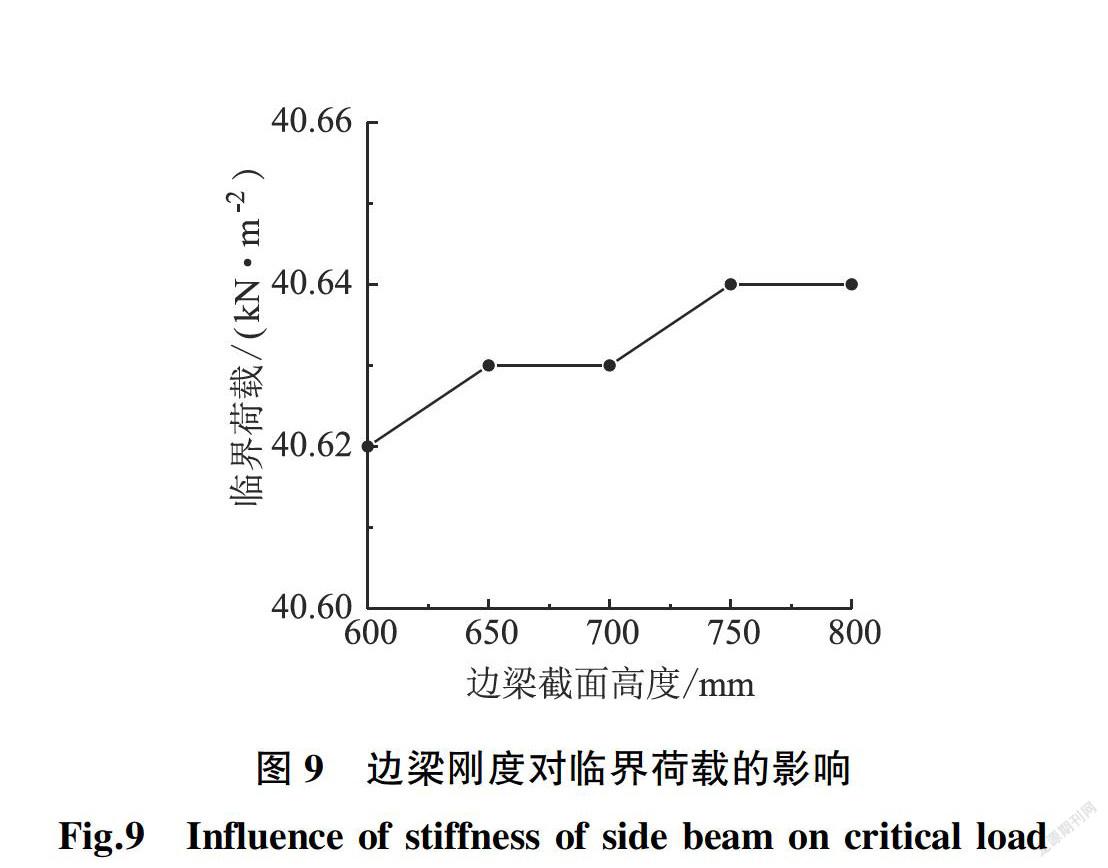
仅改变边梁的截面高度共分析5个算例，边梁截面高度由0.60 m渐变至0.80 m，以50 mm为级差。弹性稳定临界荷载随边梁截面高度变化的结果如图9所示。

边梁截面高度改变时，临界荷载的变化较小，因此边梁的刚度对结构的临界荷载几乎没有影响。密肋平板传递的推力由边梁来平衡，而边梁抗扭刚度的影响大于抗弯刚度的影响，所以其抗弯刚度对临界荷载几乎不产生影响。因此在满足结构支承条件的前提下，建议边梁的截面高度可取其跨度的1/15～1/10。

5 结论

（1）结构的低阶弹性失稳模态与柱面拱壳具有较大的整体相似性，且模态最大位移主要出现在密肋平板上，因此设置主拱和脊线有利于提高结构的整体刚度，弹性失稳临界荷载远大于结构使用荷载。

（2）矢跨比是影響结构临界荷载的重要因素，在矢跨比为1/7～1/4时，临界荷载近似随矢跨比的增加线性增长，建议结构矢跨比不宜低于1/6。

（3）将密肋梁与屋面板的中性层重合时，屋面板厚度的改变对结构弹性失稳临界荷载的影响较小，因此屋面板的厚度可按网格短边尺寸的1/30确定。

（4）增大密肋梁刚度能有效提高结构的整体刚度，进而提高其弹性稳定承载力，密肋梁截面高度可按结构跨度的1/100～1/80确定。

（5）主拱是結构的主要受力构件，增大其刚度能有效提高结构抵抗弹性失稳的能力，建议主拱截面高度可按屋盖跨度的1/70～1/50取值。

（6）脊线梁和边梁刚度的改变几乎不会对结构的临界荷载产生影响。

参考文献：

[1]董石麟.空间结构的发展历史、创新、形式分类与实践应用[J].空间结构，2009，15（3）：21-43.

[2]方小丹，曾宪武.华南理工大学体育馆预应力钢筋混凝土双曲抛物面组合扭壳设计[J].建筑结构学报，2011，32（8）：18-25.

[3]于东晖，奥晓磊，毕大勇.银川火车站站房混凝土拱壳结构稳定性能分析[J].建筑结构，2011，41（9）：99-103.

[4]吴族平，张利，龚景海，等.某椭球形气膜钢筋混凝土壳体结构力学性能分析[J].工业建筑，2016，46（s）：324-329.

[5]KROMOSER B，KOLLEGGER J.Pneumatic forming of hardened concrete￣building shells in the 21st century[J].Structural Concrete，2015，16（2）：161-171.

[6]TENG J G.Steel￣concrete composite shells for enclosing large space steel&composite structure[C]//Proceedings of International Conference on Steel and Composite Structures.Korea： Techo-Press，2001：403-409.

[7]常玉珍，吴敏哲.组合肋壳结构静力特性分析[J].建筑结构，2009，39（4）：54-56.

[8]孔煜，代富红，严标.混合型网壳结构的有限元法分析及受力特性的研究[J].贵州工业大学学报（自然科学版），2002，31（5）：81-85.

[9]董石麟，罗尧治，赵阳.新型空间结构分析、设计与施工[M].北京：人民交通出版社，2006.

[10]董继斌.组合网壳设计[J].特种结构，1998，15（4）：12-15.

[11]EHSAN S，ALEXANDER S，JOSER H，et al.Structural behavior of a lightweight，textile￣reinforced concrete barrel vault shell[J].Composite Structures，2017，69（3）：505-514.

[12]张华刚，马克俭，杨期柱.混凝土大跨度密肋式折板壳的结构形式与分类[J].贵州工业大学学报（自然科学版），2008，37（4）：55-59.

[13]张华刚，杨期柱，马克俭，等.人字形密肋式折板拱壳的静力性能分析及其工程应用[J].建筑结构学报，2009，30（s2）：29-35.

[14]柳勇斌，张华刚，吴琴，等.混凝土折板形柱面网壳静力性能的参数化分析[J].空间结构，2019，25（2）：78-86.

[15]柳勇斌，张华刚，方强，等.混凝土棱柱面网壳动力特性的参数化分析[J].贵州大学学报（自然科学版），2018，35（4）：100-105.

[16]沈世钊，陈昕.网壳结构稳定性[M].北京：科学出版社，1999.

[17]龙驭球，包世华.结构力学[M].北京：高等教育出版社，2006.

（责任编辑：周晓南）

Elastic Stability Analysis of Concrete Prismatic Reticulated Shell

TANG Zanhui1， ZHANG Huagang1*， WEI Wei2， ZHANG Xin1， WU Qin1

（1.Research Center of Space Structure， Guizhou University， Guiyang 550003， China;

2.Guizhou Construction Supervision & Consulting Co. Ltd.， Guiyang  550081， China）

Abstract：

Concrete prismatic reticulated shell is a new type of concrete reticulated shell structure， which is formed by cutting a series of planes from curved surfaces and then gridding each plane into a ribbed plate and intersecting at the ridge line. In order to discuss its stability performance，and to understand its buckling modes and loads， as well as the influence of the ratio of rise to span， the thickness of roof slab and the stiffness of ribbed beam， ridge line， main arch and side beam on the critical load of the structure， this paper adopts the finite element method to conduct the parametric analysis of the structural elastic stability. The results show that the low￣order instability modes of the structure and the cylindrical arch shell have a large overall similarity， and the maximum modal displacement mainly appears on the ribbed slab.It is suggested that the ratio should not be less than 1/6;The thickness of roof plate can be determined by 1/30 of the short side of the grid.Increasing the section height of the ribbed beam is beneficial to improving the elastic stability bearing capacity of the structure. The section height of the ribbed beam can be 1/100～1/80 of the span of the structure.The main arch is the main stressed structure of the roof， and its section height can be determined according to 1/70～1/50 of the span of the roof.The stiffness change of side beam and ridge beam has little effect on the critical load of the structure.

Key words：

concrete prismatic reticulated shell;elastic stability;critical load;buckling mode;the finite element method