基于滑模控制技术的视觉板球控制系统设计

韩治国 李伟 冯兴 陈能祥

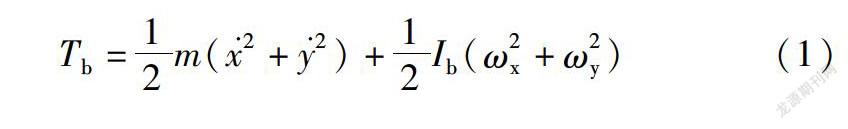
摘 要：针对视觉板球跟踪控制问题，基于线性化动力学模型，研究了基于滑模变结构控制技术的视觉板球跟踪控制。首先，根据板球系统的物理模型，推导了视觉板球的动力学模型，在小角度假设下，对建立的动力学模型进行了线性化，并建立了系统的状态空间模型。其次，针对建立的状态空间模型，通过设计线性滑模面，结合新型非线性滑模趋近律，设计了视觉板球滑模控制律，并基于Lyapunov稳定性理论，对设计的滑模控制律进行了稳定性证明。最后，将设计的控制律代入建立的状态空间模型进行仿真验证，同时与现有的控制方法（极点配置与LQR）进行对比仿真。仿真结果表明，设计的滑模控制律渐近稳定，并且具有良好的控制精度与系统收敛速度，稳定精度高，可实现视觉板球位置跟踪控制。关键词：视觉板球;位置跟踪;滑模控制;新型趋近律;Lyapunov稳定性中图分类号：TP 13

文献标识码：A 文章编号：1672-7312（2019）06-0679-06

Control system design for visual cricket based on sliding model control

HAN Zhi-guo1，LI Wei1，FENG Xing2，CHEN Neng-xiang2

（1.School of Astronautics，Northwestern Polytechnical University，Xi’an 710072，China;2.Shenzhen Qianhaigezhi Technology Co.，Ltd.，Shenzhen 518000，China）

Abstract：In this paper，aiming at the issue of visual cricket tracking control，on the basis of the linearized dynamic model，the visual cricket tracking control law based on the sliding mode control technology was studied.Firstly，according to the physical model of visual cricket system，the dynamic equation was derived.And with the small-angle hypothesis，the dynamic equation was linearized to establish the state equation.Secondly，on the basis of the linearized state equation model，the new sliding mode control law were designed through the linear sliding mode surface and the new sliding mode approaching law.And the stability of the designed sliding mode control law was proved based on the Lyapunov stability theory.Finally，the obtained control law was substituted into the linearized state equation model to carry out verification.Comparative simulations were carried out with existing control methods.The simulation results showed that the control law designed in this paper was asymptotically stable，and also had satisfactory control precision，system convergence rate and stable precision.So it could achieve the control of visual cricket tracking.

Key words：visual cricket;position tracking;sliding mode control;new type reaching law;Lyapunov stabilization

0 引 言

當前，我国在“新工科与中国教育现代化”建设的背景下，迫切需要高等院校培养具有创新能力和实际动手能力的航天科技人才，动手能力的培养面临着巨大的挑战。作为控制学科的人才培养，视觉板球系统是很好的实验平台[1-2]。视觉板球系统是进行自动控制原理、现代控制理论实验的典型实验装置，该实验装置通过工业摄像机实时拍摄平板上小球的位置，通过图像分析方法计算小球在平板上的相对位置，将得到的小球位置与实验前设定的小球理想位置进行对比，根据位置差，基于PID、LQR、滑模控制等控制理论实时控制电机的转速，控制小球在平板上进行移动，进而控制小球到达理想位置[3-5]。

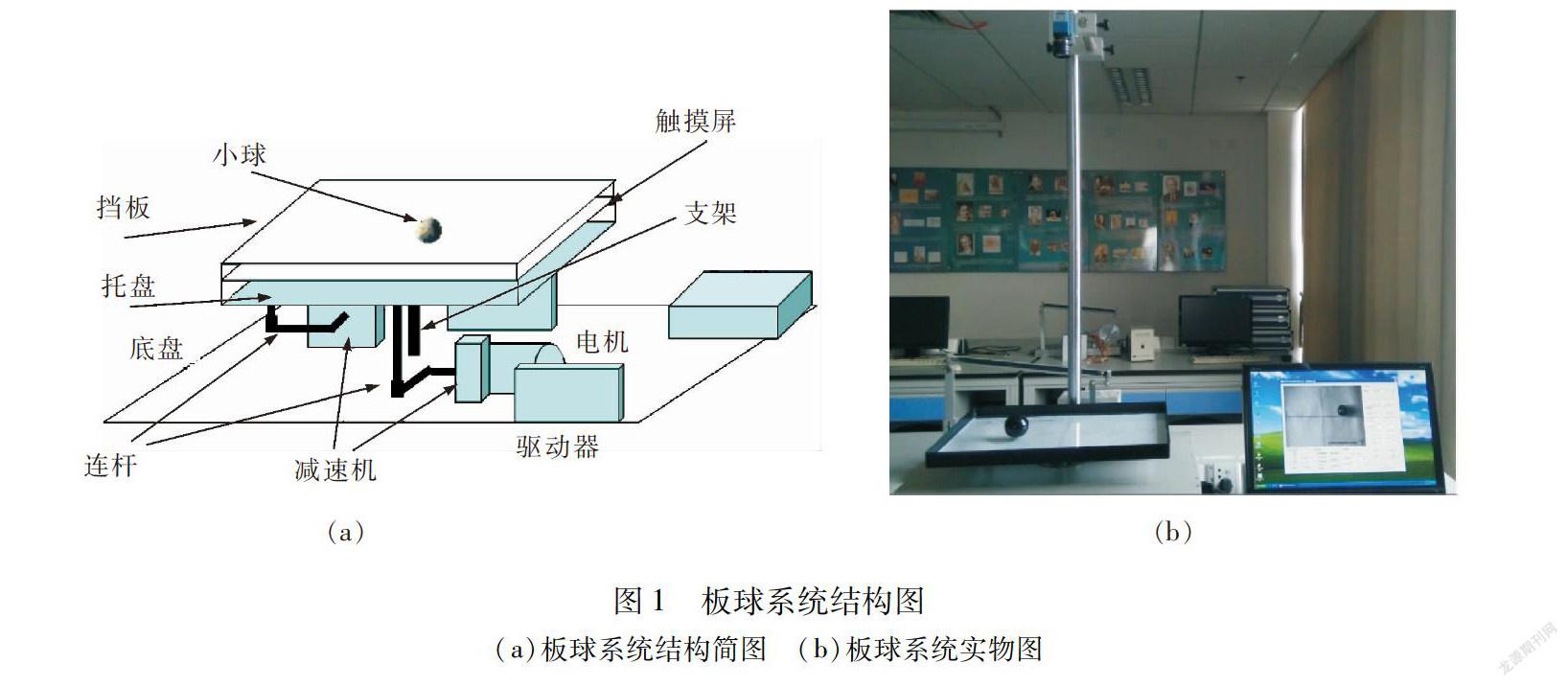
视觉板球系统的结构如图1所示，图1（a）为视觉板球原理图，图1（b）为视觉板球实物图[6]。本课题的研究目的是控制小球稳定在给定位置（该位置可任意设定，不超出视觉系统的探测范围与平板的大小即可）。

目前，针对视觉板球系统的控制器设计问题，国内许多高校进行了大量研究，如西华大学的徐云云[7]针对离散系统设计了离散滑模控制律，内蒙古科技大学的吴何琛[8]基于LQR控制理论进行控制器设计、中南大学的吕凯[9]设计了PID板球控制律、北京理工大学的董振晔[10]研究了自抗扰控制，虽然这些控制方法均取得了较为良好的控制效果，但是所设计的控制律均需较大的电机转角角加速度，不易工程实现。

文中针对视觉板球系统，在现有研究成果的基础上，基于滑模控制理论，设计滑模控制率，实现对视觉板球系统的控制。最后，通过仿真实验，验证本文设计方法的有效性，并与状态空间极点配置、LQR控制进行对比仿真，通过实验对比，进一步说明该设计方法的有效性。

1 板球系统的物理建模

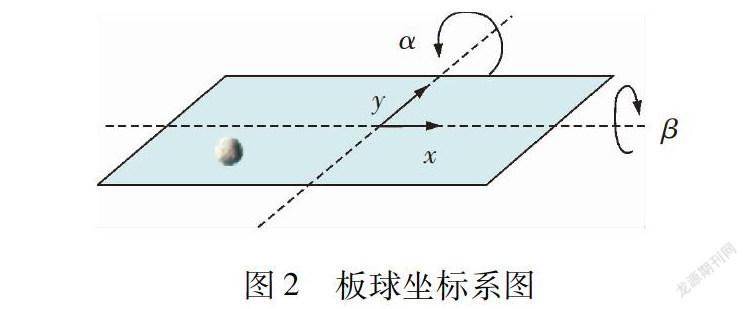
针对深圳前海格致科技有限公司设计的视觉板球系统进行研究，视觉板球的简化结构图如图2所示。在以下进行系统建模时，参考了文献[6，11-12]的建模方法。

1.1 小球的动能建模

Tb=12m（2+2）+

12Ib（ω2x+ω2y）

由于小球在运动过程中没有滑动，从而

=rbωx，=rbωy

（2）

将式（2）带入式（1），有

Tb=

12m+Ibr2b

（2+2）

（3）

1.2 平板的动能建模

Tp=12Ip（2+2）

+12（Ib+m|Ω×r|2）（2+2）

（4）

又|Ω×r|2=

（x+y）2

2+2

，代入得

Tp=12（Ib+Ip）

（2+2）+12m

（x+y）2

（5）

1.3 零势能点选择为坐标原点

则小球势能为

Vb=mg（xsinα+ysinβ）

（6）

并将式（5）和式（6）带入拉格朗日方程

ddt

L

i

-L

i=Qi

，得系统的方程组为

x：m+Ibr2b

-m（x2+y）+mgsinα=0

y：m+Ibr2b

-m（y2+y）+mgsinβ=0

α：（Ib+Ip+mx2）+mgxcosα+m（xy+y+x+2x）=τx

β：（Ib+Ip+my2）+mgycosβ+m（xy+y+x+2x）=τy

（7）

1.5 板球系统的模型简化

由于板的转动角度范围不大（±6°），在小角度下有

sinα≈α，sinβ≈β.从而对稳定状态附近微分方程式（7）中式（a），（b）进行线性化得

x：m+Ibr2b

+mgα=0

y：m+Ibr2b

+mgβ=0

（8）

取

x，，

α，，y，，β，为系统的状态，平板的角加速度为控制量。令

x=[x1，x2，x3，x4，x5，x6，x7，x8]T

=[x，，

α，，y，，β，]T，y=xu=

[，]T

則系统的状态空间描述方程为[4]

=Ax+Bu

y=x

（9）

其中，矩阵A，B参见文献[6]。取g=9.81 m/s2，小球的转动惯量

Ib=25mr2b

，带入中，有g=7.007.当设

xx=[x1，x2，x3，x4]T，

xy=[x5，x6，x7，x8]T，

可得

x

=1

2

3

4

=Axxx

+bxux，yx=[1，0，0，0]xx，

Ax=

0100

00-7.0070

0001

0000

通过式（10）和式（11）可以看出，x，y方向的运动状态是解耦的且系统模型完全一致，因此本文只针对x方向进行控制系统设计。

2 滑模控制器设计

2.1 控制律设计

滑模控制系统中的运动过程可由2个阶段组成：第一阶段是趋近阶段，它完全位于滑模面之外，或者有限次的穿过滑模面;第二阶段是滑动模态，完全位于滑模面上的滑动模态区[13-15]。因此，可将滑模变结构控制

u（x，t）分为切换控制与等效控制：即

un（x，t）

与

ueq（x，t）.

文中针对线性化板球控制方程，采用如下的滑模面[16-17]

S（x，t）=Cx

（12）

式中 S（x，t）为设计的滑模面，是关于状态与时间的函数;

C为适维矩阵。

为使系统能快速接近切换面，并且改善其抖振现象，采用新型趋近律[18-20]

=-εfal（s，η，δ）-karsh（s）

其中，0<δ<1，η>0，ε>0，δ为fal（s，η，δ）在原点附近正负对称线性段的区间长度，并且fal（s，η，δ）为非连续函数。

针对文中设计的滑模面（12）与趋近律（13），设计的控制律如下式所示

u（x，t）=

ueq（x，t）+un（x，t）

un（x，t）=-（CB）-1（εfal（s，η，δ）+karsh（s））（17）

2.2 稳定性证明

证明：选择如下的Lyapunov函数

V=12ST（x，t）S（x，t）

（18）

对上式求导可得

=ST（x，t）（x，t）

=ST（x，t）C

=ST（x，t）C（Ax+Bu）

（19）

将设计的控制律式（15）～式（17）带入式（19），可得

=ST（x，t）（CAx+CBu）

=

ST（x，t）（CAx-CAx-εfal（s，η，δ）-karsh（s））

=ST（x，t）（-εfal（s，η，δ）-karsh（s））

=-ST（x，t）（εfal（s，η，δ）+karsh（s））≤0

因此，文中设计的控制律渐进稳定。

3 仿真分析

文中针对系统模型（10），采用设计的控制律（15）进行仿真验证。系统模型参数见式（10），滑模面参数：δ=0.02，k=6，η=0.5，ε=0.01.设定的小球跟踪位置为x=0.2.

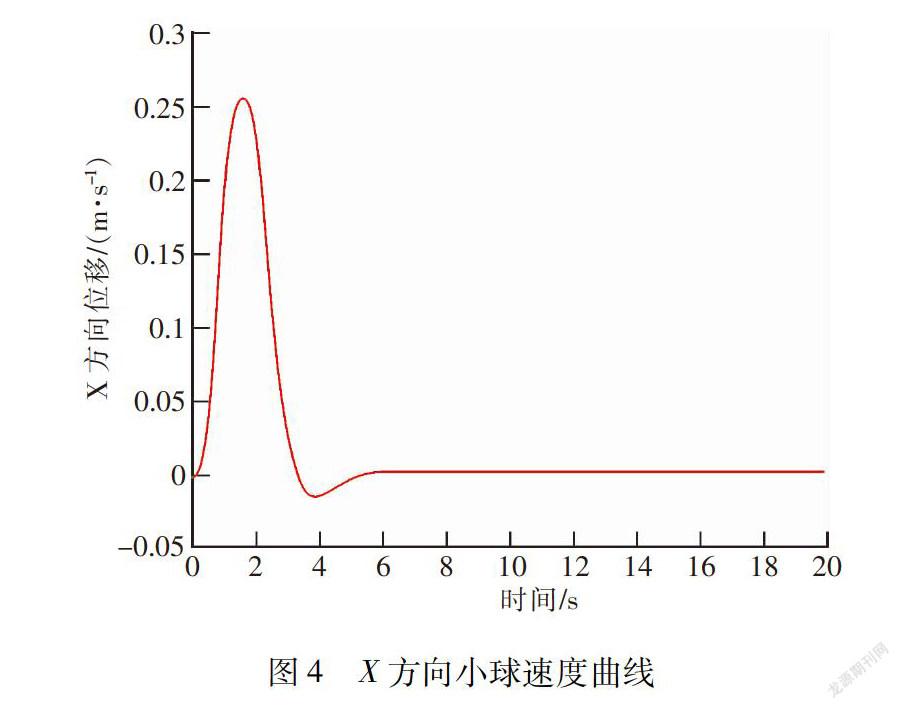
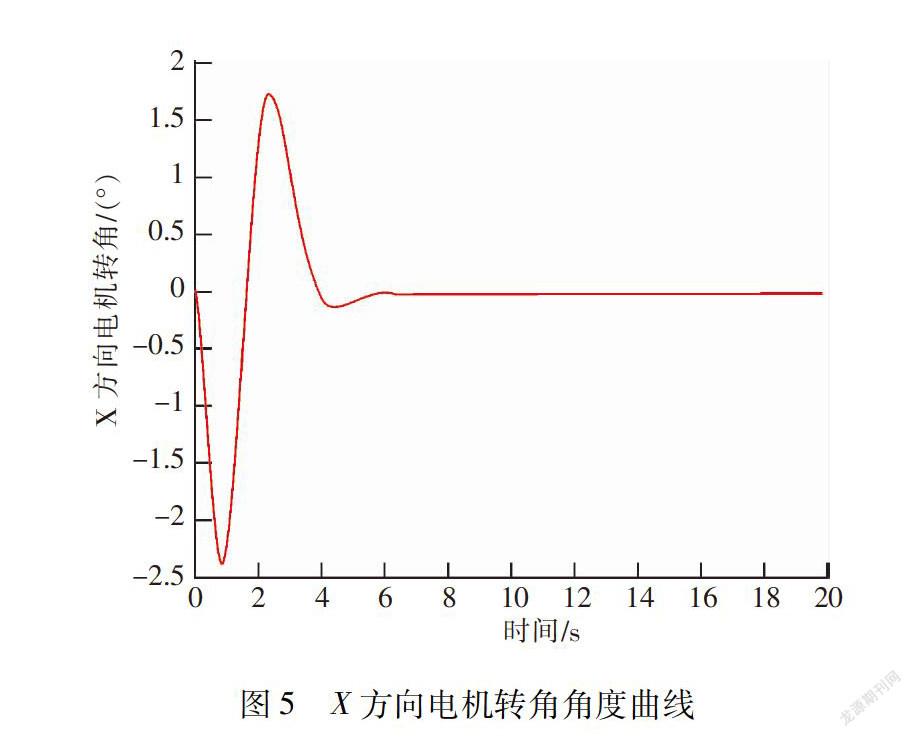
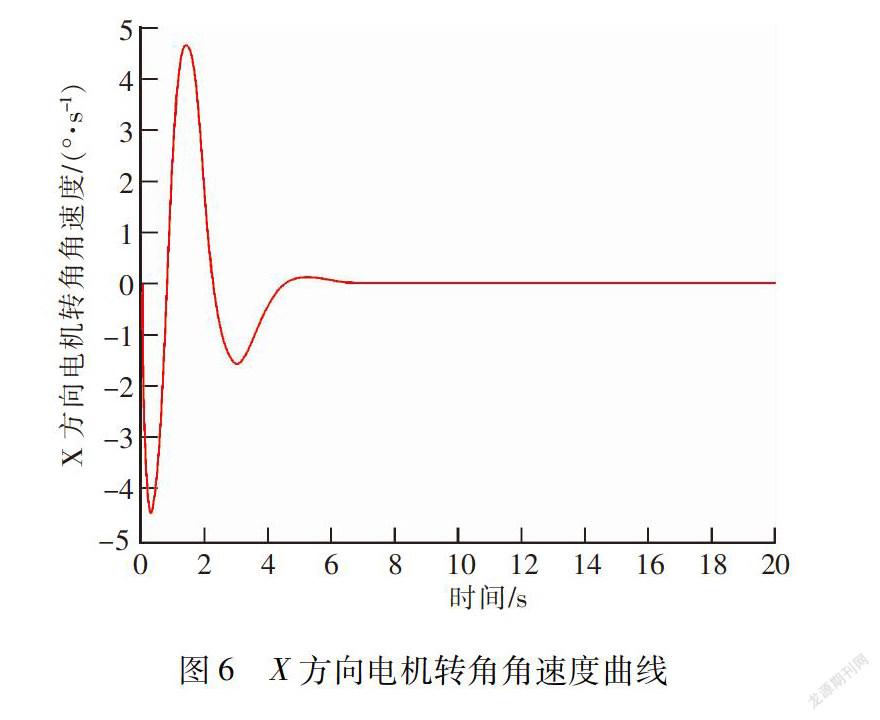
根据给定的仿真参数，仿真结果如图3～图8所示。 图3为小球位移曲线，可以看出，经过6 s左右，小球能够稳定到给定位置，稳态误差为1.073 6×10-10. 图4为小球移动过程中小球速度曲线，同样，经过6 s左右，小球的速度几乎为0.图5为小球移动过程中，电机转角曲线，图6为电机转角角速度曲线。从图中可以看出，电机转角角度范围为[-2.5，2]，电机转角角速度范围为[-5，5]。

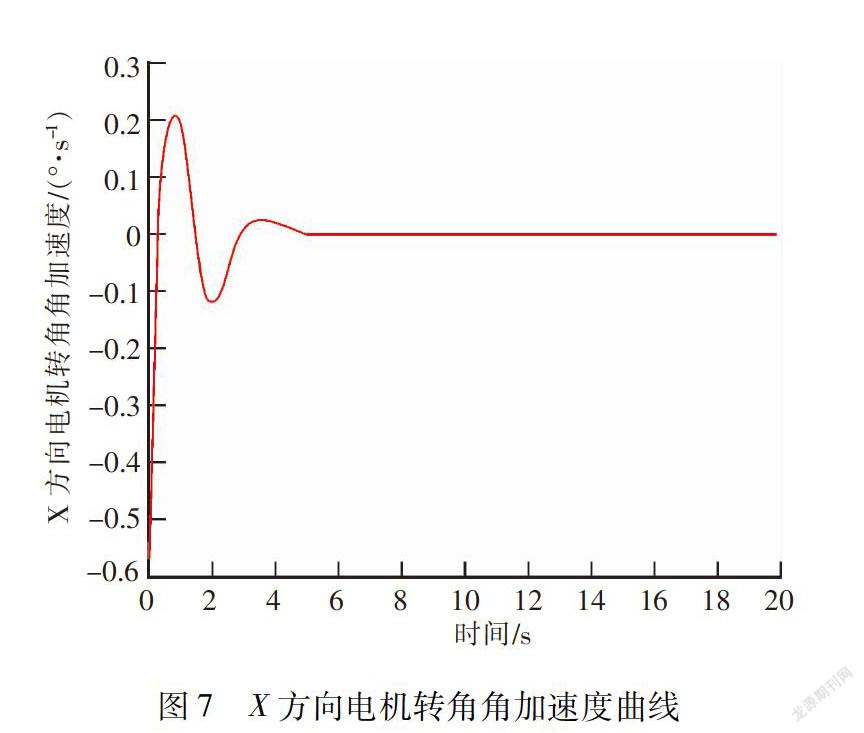
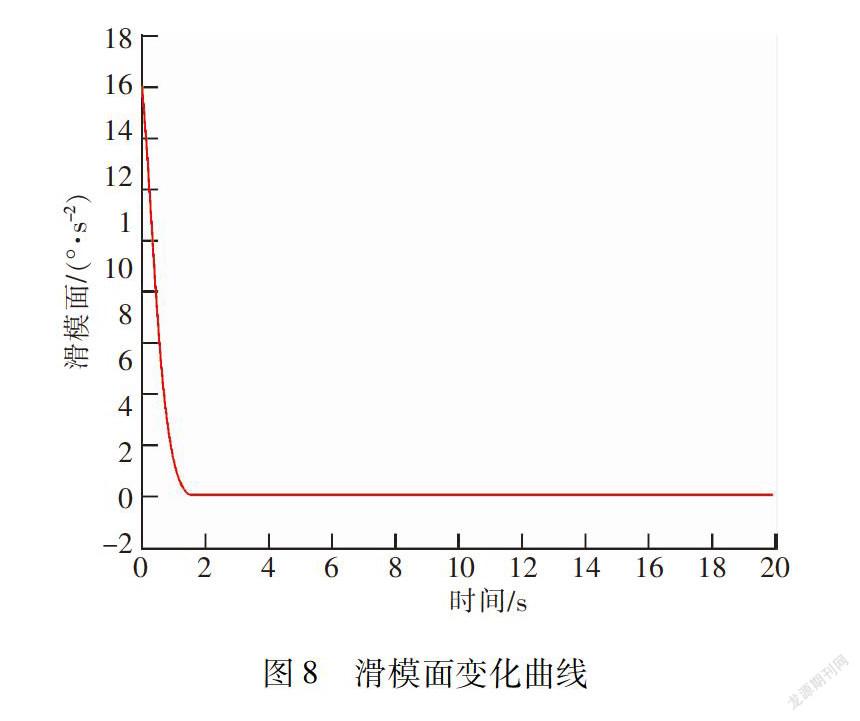
图7为小球移动过程中，电机的角加速度曲线，即系统的控制律，从图中可以看出，在小球移动过程中，电机角加速度曲线变化非常平稳，大约6 s后，电机停止转动，小球稳定在给定的位置上，电机转角角加速度范围为[-0.6，0.3]。图8为文中设计的滑模面变化曲线，可以看出，大约2 s左右，系统回到滑模面附近，2 s之后，系统能够稳定的维持滑模运动，稳定精度为2.711×10-15.综合仿真结果可以看出，文中设计的控制律具有较高稳定控制精度。

为了说明本文设计的控制律的有效性，与采用极点配置法以及LQR控制法进行对比[6，20]，控制器参数为：极点配置，K=[-14.985 0，-16.554 9，54，12，LQR控制，

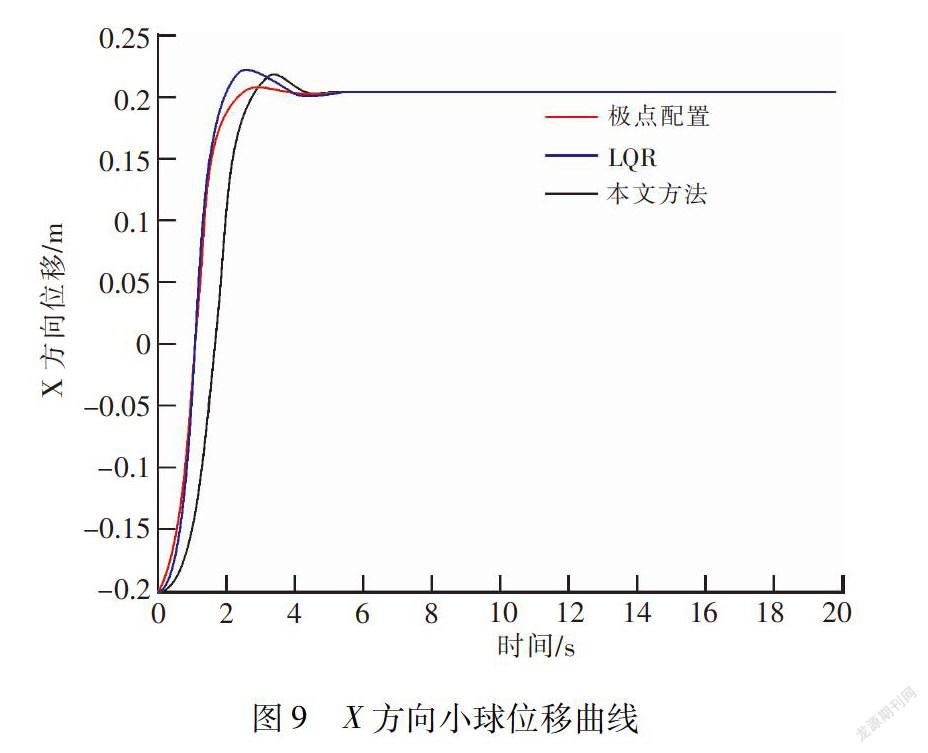
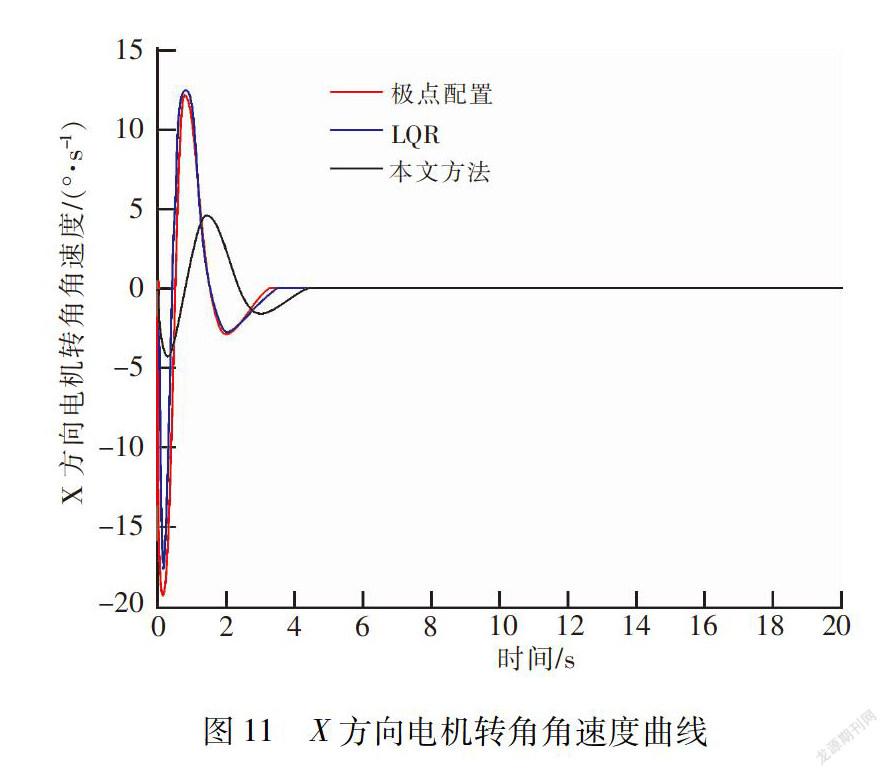
K=[-12.247 4，-12.692 5，45.512 8，9.799 3]。仿真结果如图9～图12所示。从图9可以看出，采用极点配置法与LQR控制，均能过使系统稳定到给定的位置，系统稳定精度为：

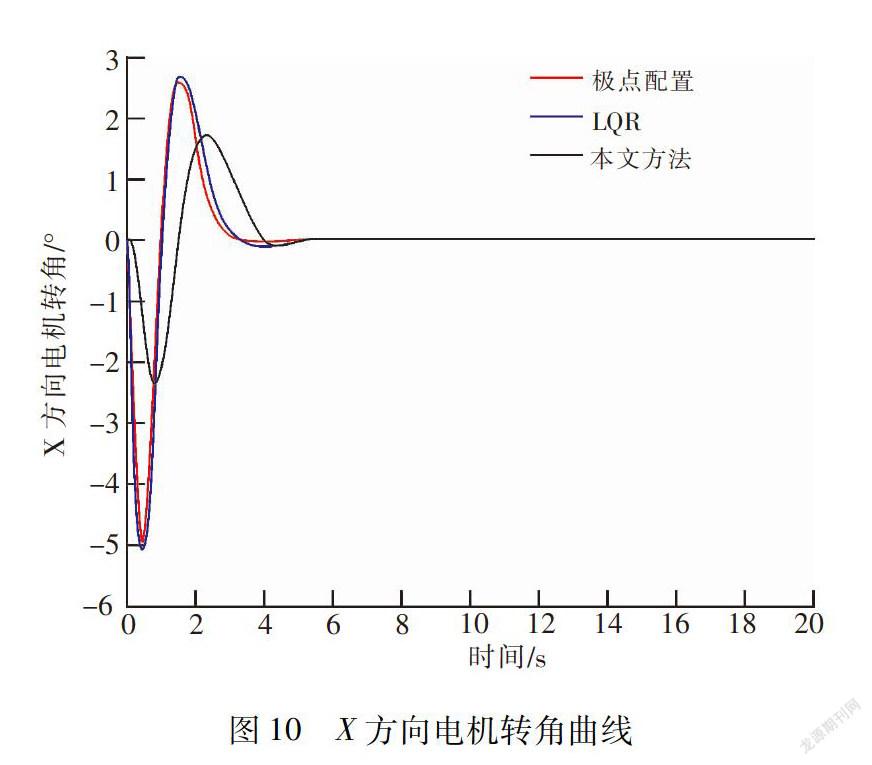
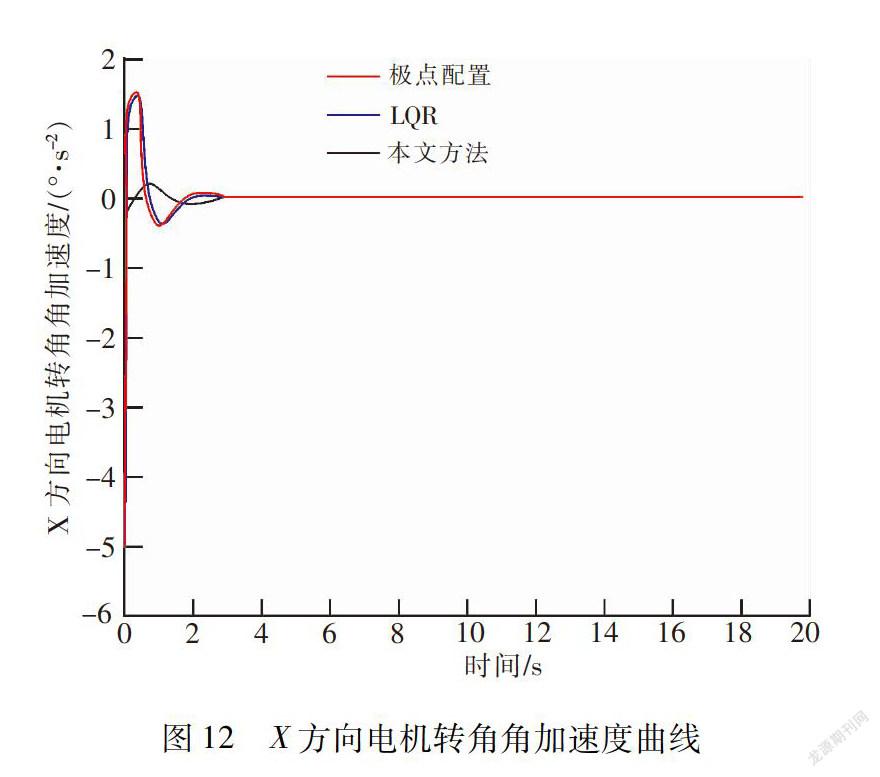
1.895 7×10-4.虽然系统的稳定时间较短，控制精度较高。但是，从图10看出，电机转角角度范围为[-6，3]，从图11看出，电机转角角速度范围为[-25，15]，从图12看出，电机转角角加速度范围为[-6，2]。跟文中设计的控制下相比，采用极点配置法与LQR控制，电机的转角、角速度、角加速度均大大的高于文中设计的控制律的参数范围，对电机的性能要求较大。因此，通过对比，文中设计的控制律控制精度高，电机的转角、角速度、角加速度变化范围小，对电机的性能要求低。

4 结 语

研究了基于滑模控制理论的视觉板球控制问题。根据板球系统的物理模型，推导了系统的动力学模型，在小角度假设下，对建立的动力学模型进行线性化，建立了系统的状态空间模型。针对建立的状态空间模型，通过设计线性滑模面和新型非线性滑模趋近律，设计了基于滑模控制的视觉板球控制方案，并基于Lyapunov稳定性理论，对设计的控制律进行了稳定性证明。同时，将设计的控制律代入建立的状态空间模型进行仿真验证，仿真结果验证了文中设计方法的有效性。为了进一步说明文中设计方法的有效性，将本文设计方法与现有控制方法进行对比仿真，通过对电机转角、电机转角角速度、电机转角角加速度等參数的对比可以看出，文中设计的控制律不仅具有较高的位置控制精度，而且需要的电机转角较小，便于工程实现。

参考文献：

[1]周 静，刘全菊，张 青.新工科背景下实践教学模式的改革与构建[J].实验技术与管理，2018，35（03）： 165-169.

[2]刘 黎.基于研究生协同培养机制建设的探究与实践[J].技术与创新管理，2019，40（03）：371-375+389.

[3]李 芳.板球系统设计及控制系统研究[D].包头：内蒙古科技大学，2013.

[4]苑仁令，向凤红，毛剑琳，等.基于视觉检测板球系统的RBF-PID控制研究[J].电子科技，2018（05）： 23-27.

[5]谢丽蓉.基于Matlab/GUI异步电动机人机界面设计[J].实验技术与管理，2014（08）： 50-53.

[6]冯 兴.视觉板球系统实验指导书[M].深圳：深圳市元创兴科技有限公司，2016.

[7]徐云云.基于视觉的板球控制系统算法研究[D].成都：西华大学，2012.

[8]吴何琛.基于视觉检测的板球系统控制研究[D].包头： 内蒙古科技大学，2014.

[9]吕凯.基于视觉传感的板球系统的控制实现[D].长沙：中南大学，2007.

[10]董振晔.基于自抗扰的板球系统控制研究[D].北京：北京理工大学，2016.

[11]翟晨汐，李洪兴.板球系统的直接自适应模糊滑模控制[J].计算机仿真，2016，33（02）： 383-388+432.

[12]韩京元，田彦涛，孔英秀，等.板球系统自适应解耦滑模控制[J].吉林大学学报（工学版），2014，44（03）： 718-725.

[13]李蒙蒙，叶洪涛，罗文广.带饱和函数的幂次新型滑模趋近律设计与分析[J].计算机应用研究，2019（05）： 1400-1402.

[14]姜立标，吴中伟.基于趋近律滑模控制的智能车辆轨迹跟踪研究[J].农业机械学报，2018（3）： 381-386.

[15]高 强，王晨光.基于模糊增益调整的双关节机械手滑模轨迹跟踪控制[J].实验室研究与探索，2012（11）： 78-81.

[16]刘金琨，孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用，2007（03）： 407-418.

[17]郝 伟，张宏立.板球系统的反演自适应动态滑模控制[J].电子技术应用，2018，44（07）： 139-142+146.

[18]郝 伟，张宏立.基于干扰观测器的板球系统非奇异终端滑模控制研究[J].科学技术与工，2017，17（33）： 119-124.

[19]李 伟，员 海，刘 磊.三轴气浮卫星实验平台研制[J].实验技术与管理，2018，35（10）：96-101.

[20]胡寿松.自动控制原理（第6版）[M].北京：科学出版社，2013.

（责任编辑：张 江）