数形结合在小学数学中的应用

龙碧谊

摘 要：數与形相结合的教学策略不仅有利于培养学生观察图形的能力，提高学生对数学的敏感性，而且可以化抽象为直觉，有利于学生理解数学内容和解决数学问题。笔者在数学教学的过程中，充分利用数形结合的解题策略进行引导，构建知识网络，更好地为学生解决数学问题提供有效途径和重要方法，将数形结合思想融入学生的解题思路与解题习惯中，从而提升学生解决数学问题的能力。

关键词：小学数学;数形结合;教学策略

在数学教学中，通过数与形之间的对应和转化来解决数学问题中的“数”不单纯地指某个数，可以指数量关系，也可以指数理，这就是数形结合。它包括形辅助数和形求解数两个方面。利用它可以简化复杂问题，使抽象问题具体化。它有严格的数字和直观的形式力量，是优化求解过程的重要方法之一，是一种基本的数学方法。

一、数形结合，易于建立数学模型

在教“3×2”的时候，笔者充分利用了点子图，结合点子图让学生理解乘法中“3”的含义。算式中的“2”表示什么？学生可以清楚地看到，它们可以表示三列和两行，也可以通过操作点子图来表示两行和三列。这一教学过程让学生充分体验从形象思维到抽象思维的数学化过程，从不同角度去理解乘法算式的意义，更好地将乘法的内在含义从隐性化为显性，建立乘法的直观模型，为后续学习乘法口诀、乘法应用题和运算定律奠定基础。

二、数形结合，联想先行，媒体验证

爱因斯坦曾经说过：“想象力比知识更重要，因为知识是有限的，想象力总结了世界上的一切。”例如，当一个立方米的立方体被切割成一个立方厘米的立方体时，一个立方米的立方体能被切割成多少个立方厘米立方体？如果这些立方体排成一行要多长距离呢？

笔者抛出问题让学生展开联想，学生有一定的空间想象能力，借助想象，头脑中形成切割长方体的表象，再去想把所有的小正方体排成一行。待学生想象后，笔者又通过多媒体直观、形象地演示整个过程，学生水到渠成地解决这一问题。从联想过渡到媒体验证，学生抽象的思维得以具体化，学生能更好地解决此问题：棱长1米的正方体每条棱都均分成10等分，变成一个由1000个1立方分米小正方体组成的大立方体，然后把1000个小立方体摆成一行，就是100米。

这样，学生不但感受图形转化的思想，还体会到数学的无限魅力。

三、数形结合，为学生构建知识网络

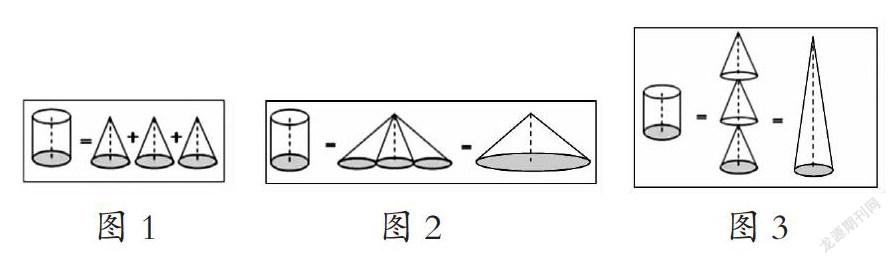
数学知识不是孤立存在的，而是相互关联的。通过图形交流，学生能更清晰地理解知识之间的联系，构建知识网络。例如，当教授“圆锥体积是等底等高圆柱体积”的知识点时，如何让学生构造圆锥与圆柱之间的关系？笔者先让学生通过动手操作感悟圆锥与圆柱体积之间的关系，再借助图像使之形象化，直观地理解与构建圆柱与圆锥的关系：如果圆柱和圆锥底面积和高相等，那么圆柱体积是圆锥的3倍;如果圆柱和圆锥体积和高相等，那么圆锥的底面积是圆柱的3倍;如果圆柱体和圆锥体的体积和底面积相等，则圆柱体的高度是圆锥体的。

“形”不仅带出圆锥与圆柱的数量关系，还更好地帮助学生思考和理解底面积、高、体积等知识之间的联系，构建圆柱和圆锥体积的知识网络。

四、数形结合，沟通数学与生活的纽带

又如在学习同分母分数加、减法时，笔者让学生借助上面的玩具拼图动手操作摆玩具、说算理，这样不但能让学生更深刻地理解分数加、减法算理，计算结果还可以继续用积木加以验证。

五、数形结合，培养数学观察能力

在小学数学教学中，教师需要引导学生通过图形与图形的结合，提高数字与图形的观察能力，从而提高学生的推理思维能力。例如教师引导学生学习人教版“数学广角——数与形”时，就可以将数字与图形结合，以形助思，引导学生进行观察推理。

教师将上述四组图形展示出来时先引导学生将每幅图中的白色和黑色方块进行统计，并结合自己的观察与总结去推导第五幅图应该是几个白色方块、几个黑色方块。通过数形结合的辩解验证，学生很快就能发现其中的普遍规律，解决此题的数学问题。课后，布置学生完成与数和图形有关的练习，在满足学生学习需要的同时，进一步提高学生的观察能力和思考能力。

六、数形结合，提升逻辑思维能力

小学数学教学从数形结合入手，可以增强教学的直观性，使学生更好地理解数学知识的内涵，增强学生的逻辑思维。例如在引导学生认知圆柱体时，很多学生对于圆柱体及其侧面展开图的联系可能存在认知的模糊，没有理解长方形的长与圆柱体底面半径之间的关系。

因此笔者在引导学生学习圆柱体侧面积时，设计了“给圆柱挑选衣服”的活动，通过实物的长方形和圆柱比对，让学生思考：要给圆柱的侧面穿上衣服，需要符合什么条件？通过一系列比较和思考、观察，学生发现：在圆柱体的侧面展开过程中，矩形的长度刚好等于圆柱体底部的周长，矩形的宽度等于圆柱体的高h。

在教学过程中，数理与图形的结合为学生提供了一种新的数学思维。在这种思维的影响下，学生会对知识点有更深的理解。因此，从数形相结合的角度指导学生，可以让学生对本课的知识点一目了然，更直观地加深了学生对圆柱形知识形成的理解和认识。

七、数形结合，增强数学解题能力

在数学知识的解释中，教师可以鼓励学生以属性结合的方法解决数学问题，提高学生解决问题的能力。

例如：在同分母分数分数加减法的讲解中，笔者以数与形相融合的方式逐层展开教学，引导学生分析数量关系并走向深入。例如，五年级下册99页的教学例题：一杯纯牛奶，乐乐喝半杯，感觉有点冷，就充满了热水。他又喝了一半，出去玩了。乐乐一共喝了几杯牛奶？

引导学生从对图形的分析去找出解决问题的思路和方法，实现对数学知识的理解，增强数学解题能力。

利用数形结合展开小学数学教学的研究与探索，不仅要让学生知道“数学知识是什么”，还要让学生知道“数学知识为什么”。它不仅有利于建立数学模型，建立数学知识网络，而且有利于提高学生的观察能力和数学思维的发散性，从而提高学生的数学素质，培养学生的核心素养。正所谓“数与形相随两相依，助思辨析互彰显”。

参考文献：

[1]陈蕾.让小学生感受“数形结合”的教学策略[J].上海教育科研，2016（02）.

[2]董文丹.让数学课堂充满数学思想——“数形结合”在低年级教学中的运用与反思[J].小学教学参考，2010（32）.

[3]符颖.感悟“数形结合” 体会数学魅力——数形结合思想在小学数学课堂教学例谈[J].小学教学研究，2018（14）.