小学数学课堂如何开展探究学习

唐劲兰

摘要：新课标理念下，如何引导学生有效开展探究学习，已然成为课堂教学亟待攻克的现实难题。教师要创设良好的教学情境，搭建适宜的探究平台，激发学生主动探究的欲望，引导学生经历丰富的、有趣味的、有意义的探究学习过程。小学数学课堂可以引导学生在模仿、冲突、操作中开展探究学习。

关键词：探究学习小学数学模仿冲突操作

新课标理念下，如何引导学生有效开展探究学习，已然成为课堂教学亟待攻克的现实难题。研究表明，个体的心理是在与周围环境的相互作用中发生、发展的。因此，教师要创设良好的教学情境，搭建适宜的探究平台，激发学生主动探究的欲望，引导学生经历丰富的、有趣味的、有意义的探究学习过程。以下是笔者实践与思考所得：

一、在模仿中开展探究学习

新知识的学习必须以已有的认知结构为基础。建构新知识的过程就是学习者从自己已有的认知结构中提取与新知识有联系的旧知识，并加以“固定”或“归属”的一种动态的过程。找到了有联系的旧知识，就可以模仿其结果或过程，探究学习新知识。这是最基础的探究学习方式之一。

例如，教学苏教版小学数学四年级下册《亿以内数的认识》一课，对于多位数的读法，学生已经有了四位数的读数经验，所以，教师先让学生读四位数5239，复习读数的方法——千位上是几就读几千，百位上是几就读几百，十位上是几就读几十，个位上是几就读几。接着，教师出示本节课要认识的八位数52395239，提问：“谁想试着读一读呢？”学生都争着要读。于是，教师就请大家一起读。学生整齐、响亮地读出了“五千万/二百万/三十万/九万/五千二百三十九”，读完后有的相视而笑，有的独自偷笑。这时，教师追问：“有什么问题吗？”部分学生说出了自己的感受：读了这么多个“万”字，有点麻烦。“那这个‘万’字怎么办？可以不读吗？”“不读肯定不行。”“应该先不读。”教师继续引导：“那‘万’字应该放在哪里读？”少数知道怎么读的学生开心地告诉大家：“应该放在最后一个‘万’字那儿读。”“行不行呢？我们先試着读一读。”学生将万级上的数读成“五千二百三十九万”后，露出了笑容，觉得这样很好。教师不满足于此，继续追问：“为什么要放在这里？能不能放在前面读呢？”学生思考讨论后，回答：“放在这里，我们知道前面的‘五千’‘二百’‘三十’分别是‘五千万’‘二百万’‘三十万’，因为千位、百位、十位不可能出现在万位前面。如果放在前面，比如放在‘五千万’那儿，我们就不知道后面的‘二百’‘三十’‘九’分别是‘二百万’‘三十万’‘九万’，还是‘二百’‘三十’‘九’。”教师评价总结：“非常好！这样读不仅简洁，而且没有歧义。这是数学学科的重要特征。”

这里，教师引导学生模仿已学的万以内数的读法，探究要学的亿以内数的读法，暴露出因思维惯性而产生的错误;然后引导学生深入思考，纠正错误。这样的探究学习是印象深刻的、有效的。

二、在冲突中开展探究学习

著名教育家布鲁纳说过：“学习的最好刺激是兴趣。”“没有兴趣的强制性学习将会扼杀学生探求真理的欲望。”在教学过程中，适时制造并运用认知冲突，往往能激起学生强烈的学习兴趣，促使学生主动探究。

例如，教学苏教版小学数学四年级下册《三角形分类》一课，对于判断三角形类型的方法，可以安排这样的学习活动：在一个信封里装入一个钝角三角形、一个锐角三角形、一个直角三角形，让三个三角形都只露出一个锐角，且三个锐角大小一样，让学生猜一猜露出的三个角分别对应哪一种三角形。几次猜测后，学生会感受到，只看到一个锐角，不能判断是什么三角形。接着，教师出示两个锐角，再让学生猜一猜。几次猜测后，学生会感受到，看到两个锐角，也不能判断是什么三角形;要看到全部三个角，才能准确地判断是什么三角形。当然，学生也能逐步感受到，如果两个锐角都比较小，那么是钝角三角形的可能性更大一些;如果两个锐角都比较大，那么是锐角三角形的可能性更大一些。这时，教师先出示一个钝角，再出示一个直角。学生很快就判断出分别是钝角三角形和直角三角形。于是，教师点明认知冲突，促进学生探究：“刚才大家不是觉得要看到三个角才能判断是什么三角形吗？现在怎么只看到一个角就能判断是什么三角形了？”思考讨论后，学生初步得到判断三角形类型的方法：因为每一种三角形都有两个锐角，所以只看到一个锐角或两个锐角，不能判断是什么三角形;但是只有钝角三角形有一个钝角，只有直角三角形有一个直角，所以看到一个钝角或一个直角，就能判断是什么三角形了。教师继续追问：“那么，判断锐角三角形要看到几个角呢？”有了之前的经验，学生很快就能得出结论：“要看到三个锐角，才能判断是锐角三角形。”此时，教师出示一个锐角，并说明这是三角形中最大的角，再次追问：“能判断是什么三角形吗？”学生发现能判断是锐角三角形后，教师再次点明认知冲突，促进学生探究：“刚才大家不是觉得要看到三个锐角才能判断是锐角三角形吗？现在怎么只看到一个锐角就能判断是锐角三角形了？”思考讨论后，学生完善了判断三角形类型的方法：因为三角形较小的两个角肯定是锐角，所以只要看三角形最大的角是什么角，就能判断它是什么三角形了。

这里，教师通过一连串的猜测验证与追问思考，不断激发学生的认知冲突，引领学生深入探究，从而在一次次“发现—否定—再发现”的过程中抽丝剥茧，去伪存真、去粗取精，获得更为完善的认识。

三、在操作中开展探究学习

科学探究中的发现往往来自大胆的猜测。有了猜测之后，通常需要验证或论证。虽然数学讲究基于思考、逻辑的论证，但是小学生的抽象、逻辑思维能力不强，更需要基于操作、体验的验证。在操作中开展探究学习，直观形象的素材、真切具身的体验能激活学生的思维，引导学生更好地发现。教师可在提出探究问题后，提供丰富的教学资源，引导学生在操作中进行探究。

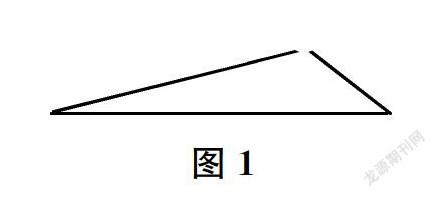
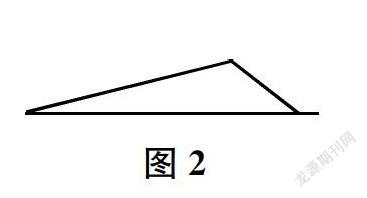
例如，教学苏教版小学数学四年级下册《三角形的三边关系》一课，教师首先呈现由三根小棒首尾相接围成的一个三角形，并提问：“这个三角形是由几根小棒首尾相接围成的？”学生回答后，教师追问：“是不是任意三根小棒都能首尾相接围成三角形？”学生回答“是”或“不是”后，教师继续追问：“怎样验证你的猜想？”学生产生通过操作来验证的意识后，教师拿出准备好的8 cm、4 cm、5 cm、2 cm的四根小棒，并提出要求：“任意选三根小棒，首尾相接围成三角形。先围一围，再记录下选择的小棒的长度，以及能否围成三角形。”多数学生记录下8 cm、4 cm、5 cm的三根小棒和4 cm、5 cm、2 cm的三根小棒都能围成三角形。少数学生记录下8 cm、5 cm、2 cm的三根小棒也能围成三角形。于是，教师故意提出“表扬”：“一些聪明的同学将8 cm、5 cm、2 cm的三根小棒也围成了三角形。其他同学都能围成吗？”受到“表扬”的学生有点得意扬扬。其他学生有的很羡慕;有的不服气，表示“这三根不能围成三角形”。教师顺势请受到“表扬”的学生上台演示给大家看。台上的学生先围出了如图1所示的图形，台下立刻有人反驳：“三根小棒没有围起来，所以不是三角形。”台上的学生又围出了如图2所示的图形，台下立刻又有人反驳：“三根小棒没有首尾相接，所以也不是三角形。”通过这样的纠错，学生加深了对三角形概念的认识，也充分认识到“不是任意三根小棒都能首尾相接围成三角形”。

这时，教师继续追问：“如果把2 cm的小棒换成3 cm的小棒，能不能围成三角形呢？”学生做出猜想后，进行操作验证。部分学生认为可以围成，教师请其中一位学生上台演示。这位学生将小棒首尾稍微错开了一点点，似乎可以围成三角形。台下立刻有人反驳：“3+5=8，两根小棒接起来和另一根小棒一样长，只能是平的，不可能拱起来。两根小棒接起来要比第三根小棒长，才能拱起来。”通过这样的纠错，三角形三边关系的初步结论已经得出。教师顺势提问：“刚才大家都认为可以围成的两种方案是不是也符合‘任意两边之和大于第三边’的规律呢？”学生立刻拿笔计算起来，通过计算验证了这一规律。

“三角形任意两边长度的和大于第三边”这一结论的探究，利用操作验证猜想，启发思维，经历纠错，从而使结论在学生头脑里留下深刻的印象，也能让学生从中体会到数学探究的基本方法。

参考文献：

[1] 孙艳明.小学数学探究式课堂教学案例研究——以C市4所小学课堂教学为例[D].长春：东北师范大学，2012.

[2] 蔡金香.小学数学自主探究性学习的实践研究[D].武汉：华中师范大学，2013.

[3] 孙淑敏.基于自主探究模式的小学数学应用题教学策略研究[D].新乡：河南师范大学，2012.