小学数学教学中“几何直观”的培养
2019-09-10彭亮徐文彬张平
彭亮 徐文彬 张平
摘要:作为“直观想象”的重要组成部分,“几何直观”是学生数学素养的重要成分。“图形的高”的教学,应该以数学知识的本质引发教学的重构,以学生的认知结构引发学习的重思,从而指向“几何直观”的培养。小学数学教学中“几何直观”的培养需要关注关联和想象的培养、运用意识的培养、与其他数学内容的联系。
关键词:几何直观图形的高关联想象数形结合
史宁中教授指出,数学中问题的解决很大程度上依赖于直观,而不是通常所认为的证明和计算。因此,“直观想象”成为高中数学学科核心素养之一。其目的是,引导当下的数学教育关注和培养学生的直观想象能力。作为“直观想象”的重要组成部分,“几何直观”是学生数学素养的重要成分。因此,研究小学数学教学中“几何直观”的培养具有重要意义。
一、“几何直观”培养的一个案例
本文选取的案例是“图形的高”的教学。
(一)教学问题
“高”是小学数学“图形与几何”的内容之一。教材一般将其安排在三角形概念之后,作为与三角形的边、角等同的几何概念来学习。教师在教学中,往往是在讲完三角形的相关概念之后,引出“由三角形的一个顶点到对边的垂直线段叫作三角形的高,这条对边叫作三角形的底”。
然而,部分学生在学完三角形的高之后,会有这样的疑问:为什么要学习三角形的高?在他们看来,三角形的高与其边、角不一样:边、角是组成三角形的必备要素,而高不是。对此,很多教师囿于教材的编排,不知道该如何处理,从而不能突出高的数学本质。
并且,部分学生在作图的过程中,还会出现这样的问题:为什么高可以横着?为什么高不一定是竖直的?因为他们在生活中遇见的高都是竖着的。对此,部分教师尝试用人体的身高来解释。如此,貌似解决了学生的疑问,但却与高的数学本质相去甚远。
同时,这样的教学也没能充分地挖掘“高”这一数学内容的几何直观内涵,进而错失了培养学生几何直观能力的契机。
(二)教学改进
从高的本质以及几何直观内涵的角度来看,“图形的高”的教学可以做以下改进:
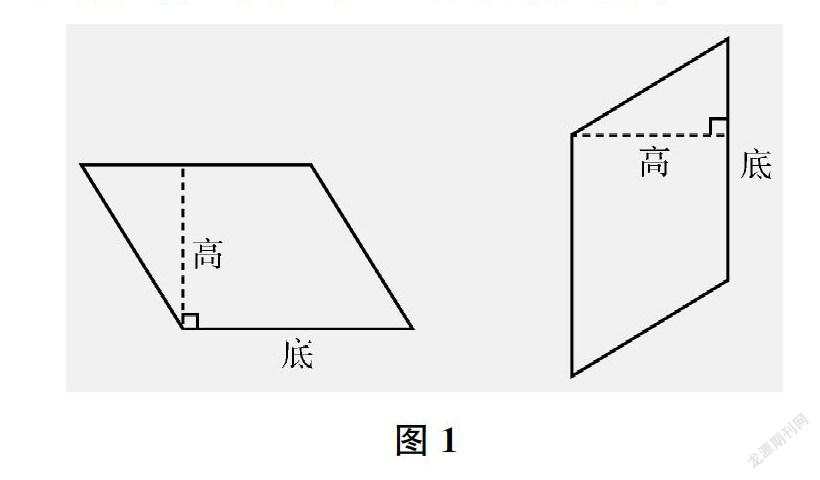
首先,呈现面积相等的平行四边形和长方形菜地,让学生思考为什么两个图形的面积相等。学生通过图形割补的办法找到两个图形之间的关系。据此,提供不同的平行四边形变式,让学生用类似的方法找到平行四边形对应的长方形。进而,引出平行四边形的“高”和“底”两个对应的概念(如图1)。
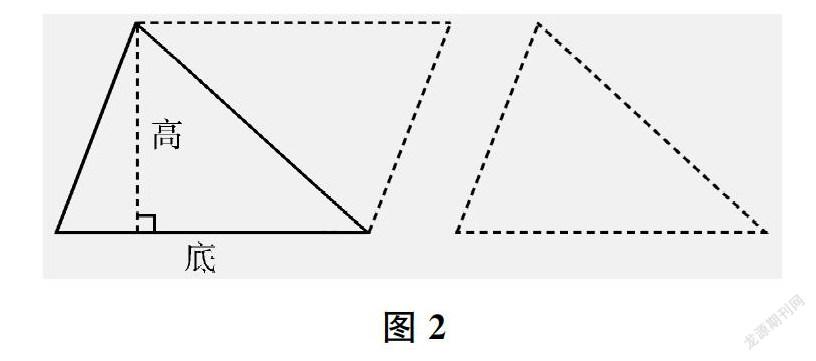
其次,呈现一个平行四边形和一个沿平行四边形对角线切分得到的三角形,让学生思考为什么三角形的面积是平行四边形的一半。学生依据上述方法找到两个图形之间的关系,从而得出三角形的高和底(如图2)。进而,以不同的三角形变式,强化三角形的高和底的概念。
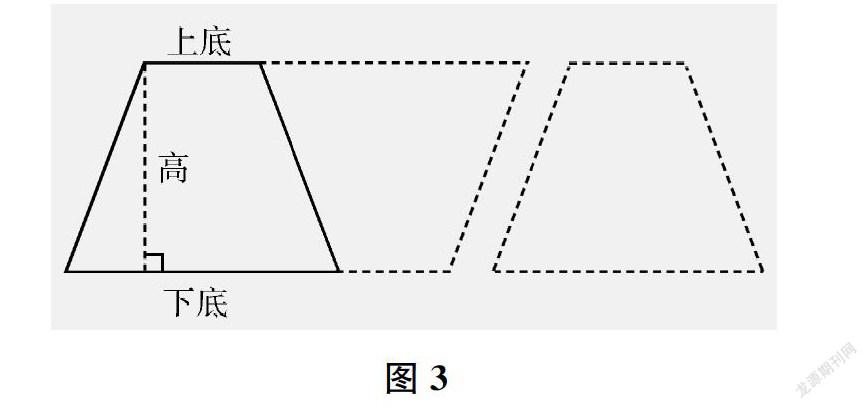
最后,呈现一个平行四边形和一个沿过平行四边形对角线交点的一条直线(非对角线)切分得到的梯形,让学生思考为什么梯形的面积是平行四边形的一半。学生依据上述方法找到两个图形之间的关系,从而得出梯形的高和上底、下底(如图3)。
(三)设计意图
1.以数学知识的本质引发教学的重构。
就“图形的高”而言,当下的小学数学教学都将其与具体图形的认识放在一起,即将其作为图形的一部分来认识。但是,“高”与图形的其他部分的不同之处在于,其不是图形原有的,也就是说,没有“高”也能够组成一个图形,并不影响图形的本质属性。因此,才会出现学生产生“为什么要学习高”的疑问的情况。实际上,从数学知识的本质上看,“高”与图形的面积密切相关,是在求解图形面积的过程中产生的。上述“图形的高”的教学设计便是基于数学知识本质的教学重构,在每一个教学环节中以不断重复的方式来指向“高”的本质。
2.以学生的认知结构引发学习的重思。
课堂教学要符合學生的认知结构,并有所提升或明晰。一般来说,认知结构关涉知识结构和认识结构两个层面。就“图形的高”的教学而言,从知识结构层面来说,学生已经认识了长方形、平行四边形、三角形以及梯形等平面图形,并对“边”“角”“周长”“面积”等几何概念有所了解;从认识结构层面来说,学生已经具备了初步的“发现—操作—验证—归纳”的数学学习能力和空间想象能力,能够对图形进行初步的转化和联系。然而,在实际教学中,一些教师往往聚焦于学生的知识结构,从学生的知识结构出发引出新知的学习。虽然这种方式能够唤醒学生的已有知识,将旧知和新知建立联系,但是,这种联系可能对学生数学学习能力的提升有所阻滞。上述“图形的高”的教学设计,没有从三角形的高引入,而是从平行四边形的高引入,其用意就是让学生能够使用已有的知识和初步的图形转化能力,发现平行四边形和长方形之间的关系,进而感受到“高”的产生;随后,逐步加大图形之间转化的难度,其目的就是对学生被唤醒的数学学习能力进行巩固和强化。因此,在这样的教学设计下,学生不仅仅是利用已有的图形知识来学习新的图形知识,更能提升已有或明晰模糊的认识结构。
3.指向“几何直观”的培养。
数学素养通常是在富有挑战性的问题的探索和解决过程中逐渐养成的,而不是在单纯的数学知识学习中获得提升的。引导学生基于自身认识结构,逐步认识数学知识的本质,或可视为培养数学素养的有效路径。上述“图形的高”的教学设计,就对学生“几何直观”的培养有所助推。比如,让学生只借助图形的高想象与之面积相等的图形,以及通过图形变换寻找图形之间的关系,这些都是“几何直观”培养的体现。具体而言,几何直观作为一种能力,其核心并非只是通过直观明晰图形的特征,更为关键的是借助几何直观学习数学知识,甚至解决数学问题。据此,让学生通过高来想象和寻找与给定图形相等面积的图形,即抓住“高”这一关键要素来学习数学知识,解决相关问题。这比只是在图形中找出高更能体现“高”这一要素在解决问题中的作用,从而真正地切中几何直观的要义。
二、“几何直观”培养的注意事项
基于上述案例,小学数学教学中“几何直观”的培养需要关注以下几个方面:
(一)关联和想象的培养
“几何直观”中“直观”的要义在于关联与想象。因而,在教学中,教师要引导学生学会在图形之间、图形要素之间寻找关系,产生关联与想象。这是培养学生“几何直观”的前提。比如,教学“图形的高”,如果分别在学习完三角形、平行四边形、梯形等图形后,介绍一下它们的高,让学生学会找出或画出它们的高,那么“高”这一要素与图形之间的关系就被割裂了。在学习之后,学生会自然地问;“为什么要学习高?”因为在学生的认知中,图形的高与图形没有任何关系。而上述“图形的高”的教学设计,则通过面积将图形的高与图形建立起关系,一方面解决了学生对“高”的困惑,另一方面有意识地培养了学生关联和想象的能力。我们可以预想到,在后续的几何学习中,学生一定会将高与面积联系起来,且通过高将不同图形联系起来,从而更好地学习知识,解决问题。
(二)运用意识的培养
史宁中教授说,并非画出几何图形就可以称为借助几何直观,而是需要借助几何图形发现所研究图形的本质、关系或规律。因此,在教学中,教师要引导学生运用几何直观学习相关的“图形与几何”内容,从而让学生感受到几何直观的价值。比如,上述“图形的高”的教学设计,从一开始的平行四边形的高到最后的梯形的高的学习,通过图形的变换,寻找面积相等的长方形,从而找到不同图形的高贯穿其中。如此,学生习得或感知这种方法之后,可以在类似的情境中迁移运用,从而强化这一解决问题的直观方法。
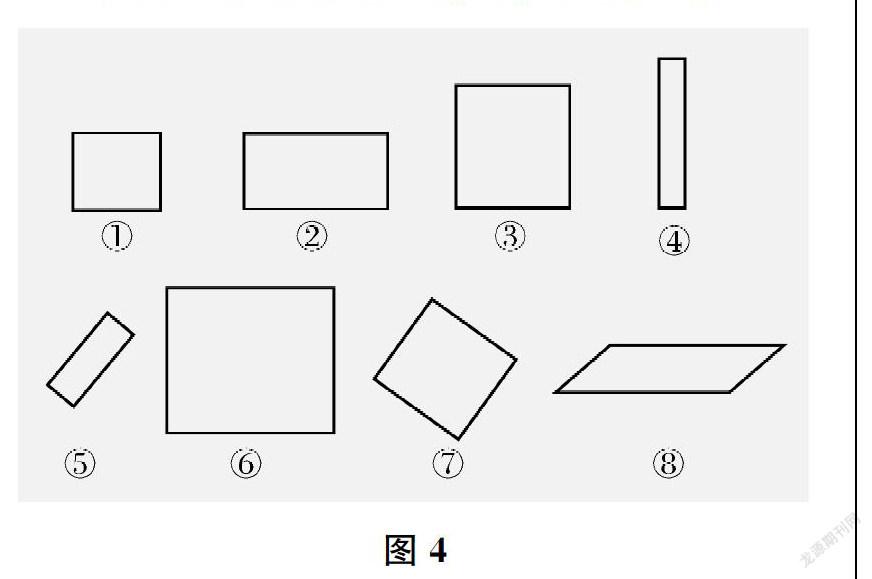
再如,教学《长方形、正方形的认识》一课,一位教师通过图形分类的方式(如下页图4),引导学生探究长方形和正方形的特征。这一做法将图形分类与几何直观很好地融合在了一起,帮助学生在不同图形之间感受可能存在的关系,进而为发现长方形和正方形的特征做好铺垫。这里,如果直接让学生通过观察或感知来探究长方形和正方形的特征,可能就错失了让学生运用几何直观的机会。而这是培养学生“几何直观”的基础。
(三)与其他数学内容的联系
几何直观作为一种能力,它的价值和意义并不局限于“图形与几何”领域。一些数学概念的理解、一些数学问题的解决都需借助于几何直观。
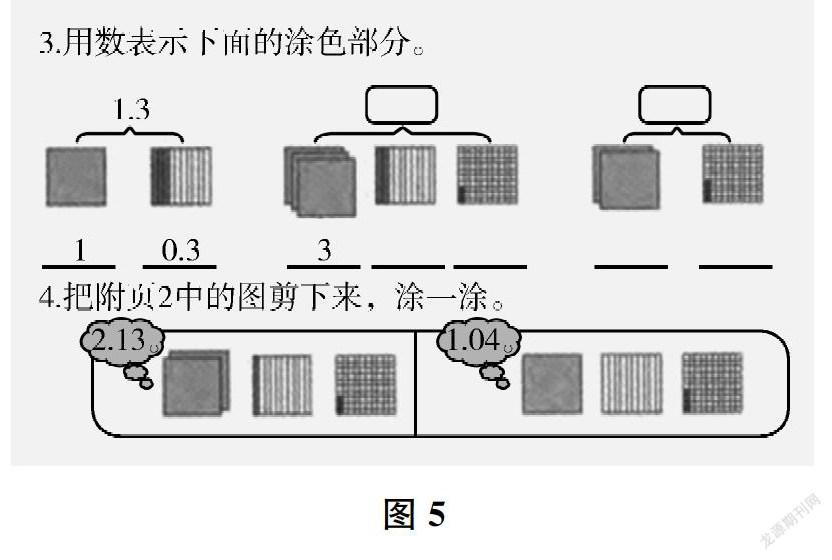
就数学概念的理解而言,几何直观具有很重要的作用。比如,北师大版小学数学四年级下册“小数的意义”内容这样编排:通过将正方形看成“1”,分别十等分后涂色和一百等分后涂色的方式,帮助学生理解十分位、百分位的位值概念以及数位之间的进位关系;通过图形(如图5),引导学生感知小数中不同位值的大小关系。通过上述图形,还可以帮助学生理解1.6和1.60等在意义上的差别。
就数学问题的解决而言,几何直观可能具有更重要的作用。解决小学数学问题时,线段图是几何直观中最为常见的形式,通过线段图可以清晰地展现题目中已知量和未知量之间的关系。此外,在教學中,教师也可以设置一些通过图形巧妙解决数学问题的例子,让学生感受几何直观的优点。比如“乌有国毒酒事件”问题:
乌有国王要举行酒会,但为酒会准备的500桶酒中有一桶被下了毒。酒会48小时后就要举行,国王决定用囚犯来试毒,不介意死多少个囚犯,只要能在酒会前找到毒酒。已知毒酒喝下去后会在23—24小时之间发作,请问最少需要多少个囚犯,才能保证在酒会举行前找到毒酒?
这一问题如果用文字表述的方式来解决,会很冗长,而且很难理解。倘若以几何直观的方式来解决,则较为简洁、清晰明了:把500桶酒摆成大约22行、23列,一个囚犯每隔一小时喝一行,另一个囚犯每隔一小时喝一列,然后通过两个囚犯毒发的时间,就可找到第一个囚犯喝的是哪一行,第二个囚犯喝的是哪一列,由此即可确定哪一桶是毒酒。这就是两个数字(数对)确定平面中任意一点位置的运用。如此,学生才会感受到利用几何直观解决问题的便利,进而有意识地学习和运用几何直观,从而形成几何直观的能力。
*本文系江苏省社会科学基金项目“互联网时代下基础教育教师教学观念的转变与实践研究”(编号:18JYC001)的阶段性研究成果。
参考文献:
[1] 张平.图形特征的认识要关注儿童的心理特点——“长方形、正方形的认识”两种设计的比较分析[J].小学数学教育,2012(11).
[2] 章勤琼.让数学具有“画面感”——例说小学数学教学中运用几何直观的可能路径[J].小学教学设计(数学),2017(9).
