也谈数学问题意识的培养
2019-09-10王平刘丽娟
王平 刘丽娟


摘要:问题意识,是指人们在认知活动中,主动发现难以解决的疑惑、实际问题及理论问题,并产生怀疑、困惑、焦虑的心理状态。这种心理驱使个体积极探索、思考,不断提出问题和解决问题。在小学数学教学中,问题意识培养的不足之处体现在:知识孤立呈现,过程封闭固化,思想浅化表达。对此,可以从知识、过程和思维的多维关联出发,培养学生的问题意识:置点入体,结构化输入,激发问题意识;故布疑阵,开放化设问,培养解题能力;思想渗透,活动化探究,提升提问能力。
关键词:问题意识多维关联 结构化开放化活动化
一、问题意识的界定及价值
问题意识,是指人们在认知活动中,主动发现难以解决的疑惑、实际问题及理论问题,并产生怀疑、困惑、焦虑的心理状态。这种心理驱使个体积极探索、思考,不断提出问题和解决问题。
思考由问题开始,学生对于知识的主动建构应该以问题为基础。“疑则有进,小疑则小进,大疑则大进。”以问题为知识建构基础的学习过程,会引领学生对已有知识、经验进行剖析、再理解,从而丰富和发展原有的认知结构。当学生产生疑惑,进行主动的探索和思考时,学生的学习便从未知到已知,又从已知走向新的未知,如此循环往复不断地向更深入的问题迈进。
苏霍姆林斯基曾说:“人的内心里有一种根深蒂固的需要——总想感到自己是发现者、研究者、探索者,在儿童的精神世界中,这种需要特别强烈。但如果不向这种需要提供养料,即不让其积极接触事实和现象,就会缺乏认识的乐趣,这种需求就会逐渐消失,求知兴趣也会与之一道熄灭。”可以说,问题意识是人原生的心理需求,培养学生的问题意识正是向“这种需要提供养料”,有利于增强学生分析和解决问题的能力,帮助学生更好地认识自然和人类社会,形成科学的世界观、实事求是的态度以及勇于探索、创新的精神。
二、数学问题意识培养中存在的问题
(一)知识孤立呈现
当下的数学教学虽然已经逐步走向有序和类化,但是很多教师还是习惯于独立呈现每块(类)内容,忽视交代与其他内容之间的关系。如教学《三角形的认识》一课,有教师会在呈现大量生活中的三角形以后,就给出概念,继而研究三角形的顶点、边、角、高等,接着围绕三角形设计很多练习。然而,整节课缺少其他平面图形的适时介入,将学生拘囿在三角形的世界里,使他们关于三角形的认知成为一个孤立的点,失去了横向关联所有平面图形,发现研究平面图形方法相似之处的可能,进而失去了提出问题的可能。
(二)过程封闭固化
教学过程理应是每个学生都可以用不同方式、从不同角度参与的开放过程,这种开放将是学生針对知识获得过程提出有深度的问题的重要起点。但是,在很多教学过程中,学生只是在不停地按照教师的指令进行研究,而对究竟为什么要这样做知之甚少。如《平行四边形的面积》一课的教学,我们时常看到这样的片段——课件展示将长方形拉成平行四边形,教师提问:长方形的面积与它的长和宽有联系,那么平行四边形的面积可能与它的什么有关系呢?接着,学生拿着教师提供的平行四边形卡片和方格纸,数出平行四边形纸片的面积。然后,师生讨论转化成的长方形与原来的平行四边形面积是否相等、长方形的长和宽与平行四边形的底和高有什么关系,以及根据长方形的面积怎样求平行四边形的面积,最终归纳出平行四边形的面积公式。
(三)思想浅化表达
数学教学中,重要方法的掌握、基本思想的体会,应该是学生经历后的提炼、类比后的顿悟,是洗去铅华的真谛,但是,在实际教学中,容易变成流于言语形式的浅化表述。如一次《解决问题的策略——假设》公开课上,有这样的片段——教师呈现例题:“全班42人去公园划船,一共租用了10只船。每只大船坐5人,每只小船坐3人。租用的大船和小船各有多少只?”提出要求:“利用所学知识,想办法解决这个问题。”两位学生分别介绍了画示意图法和列表枚举法。接下来应该是这节课最具价值的地方——初步建立数学模型,然而,教师仅用一句“这和我们做过的‘鸡兔同笼’问题是一样的”,就替代了学生思悟的过程。这使学生对于数学思想方法的理解浮于表面,无法灵活地使用。
三、多维关联,有效培养数学问题意识
(一)置点入体,结构化输入,激发问题意识
数学教学中,可以进行纵向拉伸,将单元内、单元间、年段间的相关知识组成“结构体”,通过适当的内容调整、增补,将断裂的知识结构修复完善,使学生对知识的关联有清晰的认识;也可以进行横向贯通,在想象、迁移中把具有一类特征的单元与单元建立联系,凸显它们背后共通的思维方式,丰富学生对一类“结构体”知识内涵的整体认识和把握,提升学生分类、比较、概括、抽象的能力;还可以“纵”“横”融通,把视野从单元整体结构拓展到整个年级甚至各个学段的教学长程中,在整个小学数学(甚至初中数学)教学长程的视野下审视、策划和体现结构链和块之间的关联,形成主次分明、有机渗透的教学格局。这样的关联,能够很好地激发学生的问题意识。
例如,《三角形的认识》一课的教学片段——
教师引导学生将如图1所示的图形进行分类,并说一说分类标准。学生尝试后呈现了如图2所示的分类情况。
(二)故布疑阵,开放化设问,培养解题能力
数学教学中,教师提出的问题和知识获得的过程是否开放,在很大程度上影响着学生问题意识的发展。
例如,《角的度量》一课的教学片段(课前并未统一要求准备量角器)——
师我们已经能够粗略地比较角的大小了,那么,如何才能量出角的大小呢?用你身边的材料想想办法。
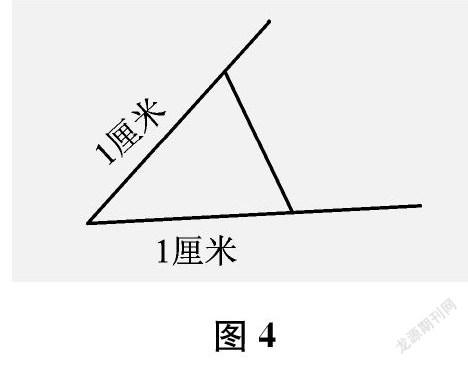
生(出示图4)用尺量。我从角的顶点出发,在两边都量1厘米的地方画点,再量这两个点形成的线段,谁长谁对的角就大。
生(出示图5)我用一个小一点的角做单位角,就像单位长度一样。把它作为标准,看每个角里有几个这样的小角。
与以往直接教学用量角器测量角的方法的封闭过程不同,这里探索测量方法的过程是开放性的。不同的学生从不同的角度参与到学习活动中来。有的对第一个同学的方法提出疑问:这样做只能比较哪个角更大一些,还是不知道每个角是多大。有的对第二个同学提出质疑:这样一次次量多麻烦啊,有没有更简便的方法?这个小角规定为多大比较合适?……正是开放化的设问,让学生获得了提出问题和解决问题的尝试;也正是这些尝试,推动课堂学习向更深处漫溯。
(三)思想渗透,活动化探究,提升提问能力
思想是行为的指引,只有具备对数学基本思想的深入理解,才能提出数学化的问题。教师应合理设计数学活动,让学生在学习的过程中领悟数学概念、公式、解题方法的来龙去脉及用途,在活动中收获体验,在体验中完成对数学基本思想的建构。
例如,《垂直与平行》一课教学,教师设计了两个探究活动:(1)动手画图,在纸上任意画出两条直线的位置。(2)交流讨论,给画出的多组位置分类,并说说分类的依据。在这两个活动中,教师引导学生经历了“对比观察位置关系—讨论分类标准—交流分类结果—抽象概括数学概念”的过程,从而积累了分类的经验、归纳的经验、抽象的经验。这样,学生经历了揭示数学概念本质的过程,在活动经验中感悟了抽象的思想。有了这样的思想渗透,学生才会自然地提出基于思想关联的数学问题。
在培养学生的数学问题意识的过程中,我们在给予学生提出问题的时间和空间的同时,应更加关注学生提出的问题的质量,从知识、过程和思维的多维关联出发,引导学生学会横向比较、纵向沟通和“纵”“横”融通地提出问题。
参考文献:
[1] 吴亚萍.“新基础教育”数学教学改革指导纲要[M].桂林:广西师范大学出版社,2009.
[2] 王永春.小学数学与数学思想方法[M].上海:华东师范大学出版社,2014.
[3] 金一民.结构化:融通数学知识的内在联系[J].江苏教育(小学教学版),2010(12).
