高中生数学核心素养评价指标研究

2019-09-10陈蓓

教育研究与评论（中学教育教学） 2019年9期

陈蓓

摘要：高中生数学核心素养评价指标研究，是数学核心素养测评研究的重点。从国际数学课程视野、国际比较测试项目的角度，分析数学核心素养评价的要素。在此基础上，对数学核心素养评价指标进行分级分类：数学抽象（数学表征、抽象思考），逻辑推理（合情推理、演绎推理），数学建模（问题提出、模型建构、解释验证），数学运算（运算法则、运算策略），直观想象（几何直观、空间想象），数据分析（获取数据、加工数据、解释数据）。并分析每一级每一类评价指标的具体内涵，确保评价标准的科学性和可行性。

关键词：数学核心素养评价指标国际数学课程国际比较测试项目

人作为社会公民，需要具备何种素养？对于此问题，教育部印发《关于全面深化课程改革落实立德树人根本任务的意见》这一文件，并发布《中国学生发展核心素养》等研究成果，使“核心素养”一词受到广泛关注。将问题聚焦到具体学科，如何培养学生的数学学科核心素养？《普通高中数学课程标准（2017年版）》（以下简称《课标》）指出，数学学科核心素养是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。

高中生数学核心素养评价指标研究，是数学核心素养测评研究的重点。本文在分析国内外一些国家和地区的数学课程以及国际比较测试项目对数学素养的要求的基础上，初步构建高中生数学核心素养评价指标的结构，分析二级指标的具体内涵。

一、数学素养评价的要素分析

（一）国际数学课程视野下的数学素养评价要素分析

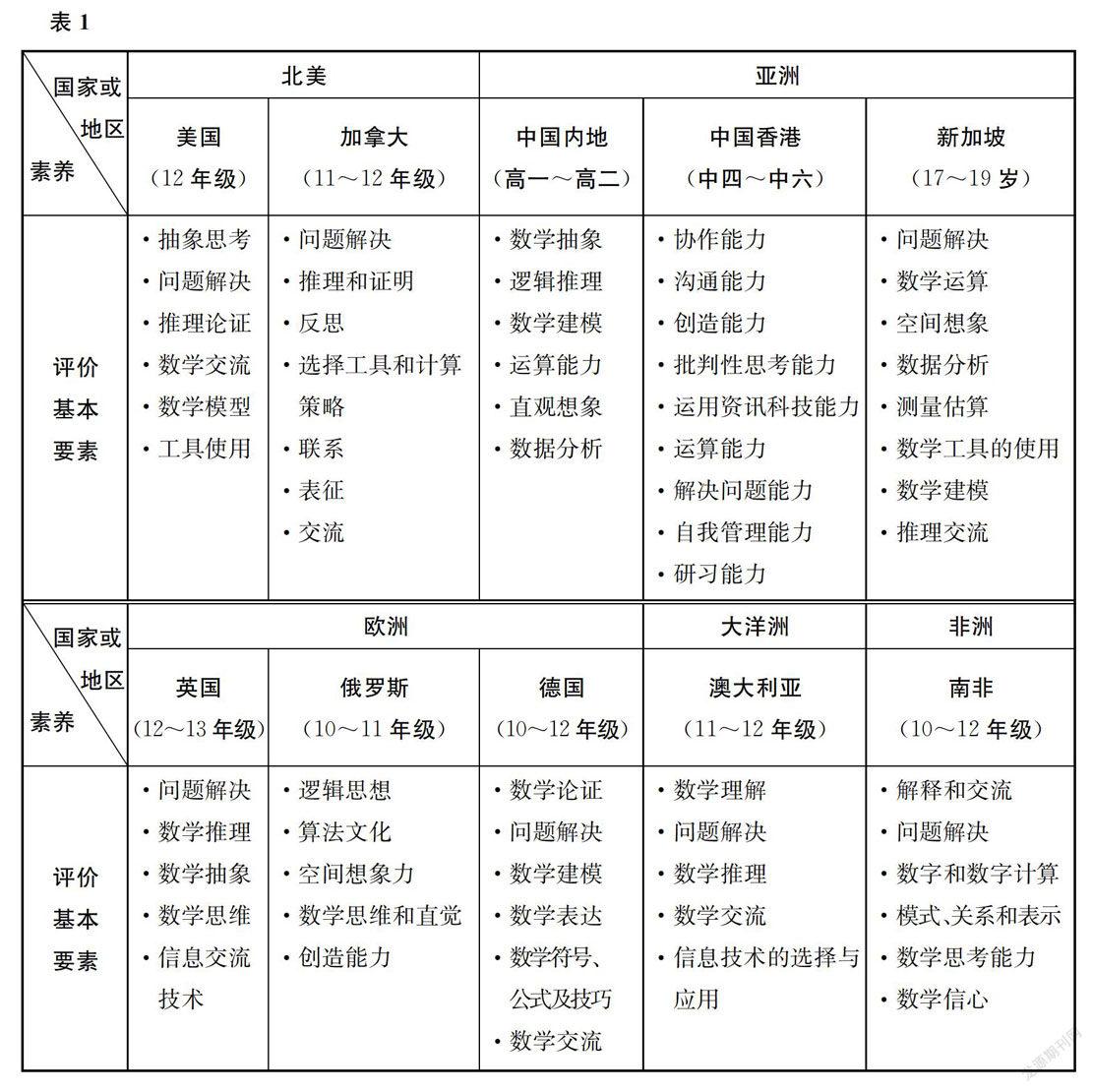
不同国家和地区在数学教育方面各有特点。学生在高中阶段，通过数学学习，获得怎样的数学素养，是我们要了解的问题。因此，从国际数学课程比较着手，分析数学素养评价要素，为构建数学核心素养评价体系提供依据。首先通过表1，分析部分国家和地区的数学素养评价要素。

1.问题解决是数学素养评价的核心要素。

通过对这些国家和地区数学素养评价要素的梳理，可以看出，学生数学素养的养成是数学课程设计的主线;同时，问题解决是数学学习的中心，它与其他各类要素互相迁移，共同促进学生数学素养的发展。

数学核心素养的发展是基础教育课程改革的深化，旨在鼓励学生在学习数学知识的同时，将其运用于现实世界。这才是数学学·数学信心习的意义之所在！数学核心素养评价要素构建的理念是培养社会发展和公民发展必需的素养。所以，几乎所有国家和地区都将“问题解决”作为数学素养评价的核心要素之一，强调数学在现实生活中的应用;同时，通过数学的学习，培养学生的批判性、逻辑性思维能力，让学生更好地分析和解决现实生活中的问题。

2.数学素养评价要素的学科性和一般性。

表中國家和地区对数学素养评价要素的分类，主要有以下两种类型：

一类是学科素养评价要素，指数学知识、技能、思想、经验以及情感、态度、价值观的综合体现。如：和数与代数知识相关的数字计算、数学符号、测量估算等素养，和图形与几何知识相关的空间想象、推理论证等素养，和统计与概率知识相关的数据分析素养，和综合与实践知识相关的数学建模素养等。这一类评价要素不仅能够体现数学课程目标，而且对应课程内容的主线，聚焦于课程要求，与学业质量评价相一致;是在学生数学知识学习过程中逐步形成的，带有数学基本特征的思维品质和关键能力。

另一类是一般意义上的素养评价要素，指学生在系统的学习中，通过体验、认识及内化等过程，逐步形成相对稳定的思考问题、解决问题的思维方法和价值观。如：工具使用、信息交流、逻辑推理、创造、协调、沟通能力等素养。这一类素养评价要素是立足于数学教学，并且渗透跨学科主题的素养;旨在发展学生数学学科素养之上的综合素养，培养学生成为自信的学习者、积极的交流者、方法的缔造者和成功的创造者。

（二）国际比较测试项目中的数学素养评价要素分析

1.PISA（国际学生评估项目）中的数学素养评价要素。

PISA（The Programme International Student Assessment）即国际学生评估项目，由OECD（经济合作与发展组织）统筹，主要以15岁中学生为对象，测评他们现实生活和终身学习所必需的知识、技能等基本要素。PISA的测试（评价）领域为阅读、数学、科学等，测试主项为数学素养，测评框架分为内容、过程和情境。

（1）PISA的四个内容领域。

PISA围绕四个领域考查数学内容。第一，空间与形状，包括空间与形状的现象及关系，主要涉及几何课程。第二，变换与关系，包括各种变化的数学表现以及各种变量间的关系等。第三，数量，涉及数字现象、数量关系及模式。第四，不确定性和数据处理，涉及概率与统计的现象与关系。

（2）PISA的四个情境维度。

PISA围绕四个维度设置问题情境：个人生活、社会性、职业和科学性。包括自然、社会、个体生活的文化背景以及职业生活、与亲友的社会生活等。在PISA中，各类情境或嵌入具体的数学问题中，或成为激发数学问题的外在情境。

（3）PISA的数学素养要素。

PISA包含表达（数学化表示情境）、运用（运用数学概念、事实、程序和原理）、评估（解释、应用和评价数学结果）三种数学过程以及七种数学基本能力（即数学素养的基本要素，见下页表2）。其中，交流素养居于所有数学素养基本要素之首。

2.TIMSS（国际数学和科学评测趋势）中的数学素养评价要素。

TIMSS（Trends in International Mathematics and Science Study）是由国际教育成就评价协会（IEA）组织的国际教育测试（评价）活动，目标对象主要是4年级和8年级学生。TIMSS中，数学素养指数学技能、数学态度与社会能力的综合。

（1）TIMSS的数学素养要素。

TIMSS针对数学素养设计了三大内容：第一，数学知识与技能，包括数与数感、测量与单位、几何、比例、函数、方程、概率、统计、数据分析、证明等;第二，数学行为与社会技能，包括日常方法的掌握、应用问题的解决、数学思想、数学交流等;第三，数学教学目标，包括传授合理的数学知识、传授基本的服务与职业的知识、唤醒对数学的兴趣、传授适当的数学观念等。

（2）TIMSS的试题设计层次。

TIMSS的试题按照如下方案来设计：一是数学知识，包括数与数感、函数、几何、数据分析、概率与统计等;二是预期的数学行为，包括应用问题的解决、数学思想、数学交流等;三是教学目标，包括传授合理的数学知识、传授适当的数学观念、激发对数学的兴趣等。

3.国际比较测试项目对高中生数学核心素养评价的启示。

PISA与TIMSS作为国际上十分有影响力的两个国际比较测试项目，在评价数学素养时，都注重真实情境在问题创设中的使用;并且采用问卷形式的过程性评价，在注重问题解决的同时，也关注基础知识和基本技能的掌握。但是，PISA以数学素养基本要素来分类，更注重数学素养的评价;TIMSS以数学来内容分类，将素养贯穿其中，更注重数学知识的评价。

（1）高中生数学核心素养评价的理念。

国际比较测试项目的素养评价理念，是让学生面向未来生活、形成终身学习的能力。PISA不仅在理念上紧跟时代所赋予素养的历史使命，还在实践层面通过对评价框架的独特设计使这一具有时代特征的素养尽可能地呈现出来。所以，高中生数学核心素养评价，应充分考量知识观、学生观和教育质量观，契合课程改革的需要，采用多元的评价主体、过程性的评价视角、多样的评价方式，更加关注学生发展所需的核心素养。

（2）构建数学核心素养评价指标体系的原则。

国际评价项目强调素养的多元性、主体性和情境性，对每一个测试指标进行了更为全面的内容设计，重视个人在素养中的主体能动性，结合素养所处的情境来开展评价。所以，构建数学核心素养评价指标体系时，应明确指标内涵，用可操作化的语言来表述评价指标，注重指标的可接受性和科学性，体现数学学科特点。

（3）数学核心素养评价试题的特征。

高中生数学核心素养的评价既要有核心内容和要求，又要有鲜明的时代特征和高中学段数学学科的特点。数学核心素养评价试题需要具有如下特征：首先，评价试题的内容应指向学生的数学核心素养，并且这样一种素养是可以通过高中数学课程的学习获得的;其次，评价试题要能对学生素养水平进行判断，对学生是否具备适应当前及未来社会的素养进行评价;最后，评价试题应契合高中数学教育的实际，贴合我国数学教育文化背景，且与未来社会发展所需要的素养接軌。

二、数学核心素养评价的指标研究

基于对国际数学课程视野、国际比较测试项目中数学素养评价要素的分析，进一步探究高中生数学核心素养评价的具体指标。有学者采用实证研究的方式，对数学核心素养的要素进行了分析。例如，喻平采用大样本问卷，统计得出数学核心素养的两种分类：其一是数学抽象、运算能力、推理能力、数学建模、数据处理、空间能力、问题解决能力、数学文化品格的八成分分类;其二是数学抽象、运算能力、推理能力、建模与数据处理、空间能力、问题解决能力、数学文化品格的七成分分类。

要建立数学核心素养的评价指标体系，一个重要的工作是构建每一个数学核心素养的二级指标。基本研究思路如下：将《课标》中的6个数学核心素养（数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析）作为评价的一级指标，然后分解出二级指标。有些二级指标是一级指标的部分有代表性的形成阶段，例如数学抽象、数学运算、直观想象、数学建模、数据分析素养的二级指标;有些二级指标则是一级指标的部分有代表性的成分，例如逻辑推理素养的二级指标。虽然二级指标不能涵盖一级指标的所有内容，但是从可测评的角度出发，均可将其作为主要评价指标。

（一）数学抽象

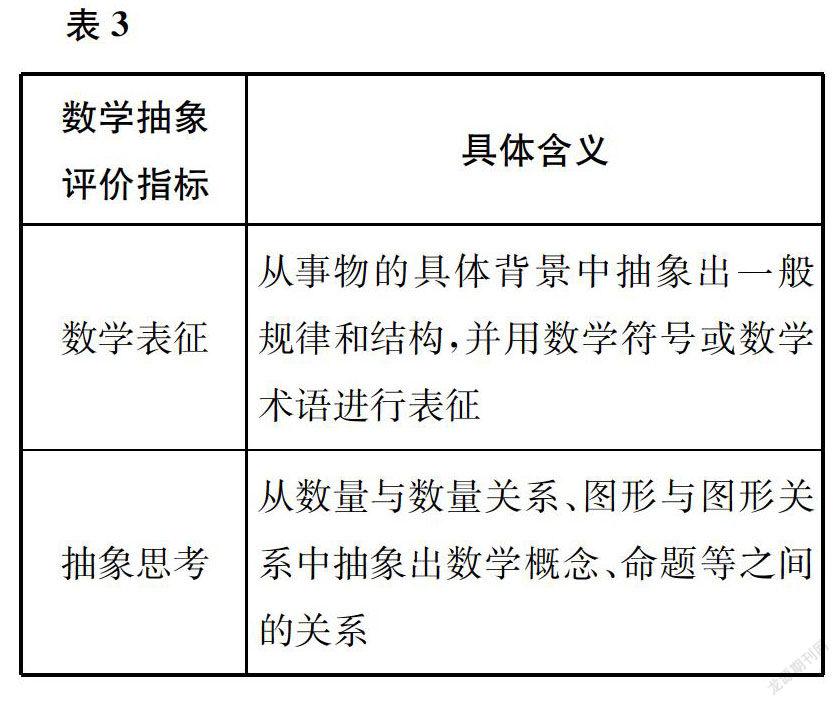
数学抽象是数学哲学的基本概念，指抽取出同类数学对象中共同的本质属性或特征，舍弃其他非本质的属性或特征的思维过程。具体而言，数学抽象指舍去事物的一切物理属性，得到数学的概念、性质、法则、命题等的思维过程。数学抽象大体上分为三个阶段：简约阶段、符号阶段和普适阶段。数学抽象包括四个过程：弱抽象、强抽象、构象化抽象和公理化抽象。数学抽象在教学上的应用分为四个层次：实物层面抽象、半符号层面抽象、符号层面抽象和形式化层面抽象。对上面的观点进行综合思考，可将数学表征、抽象思考作为数学抽象的二级指标（如表3）。

（二）逻辑推理

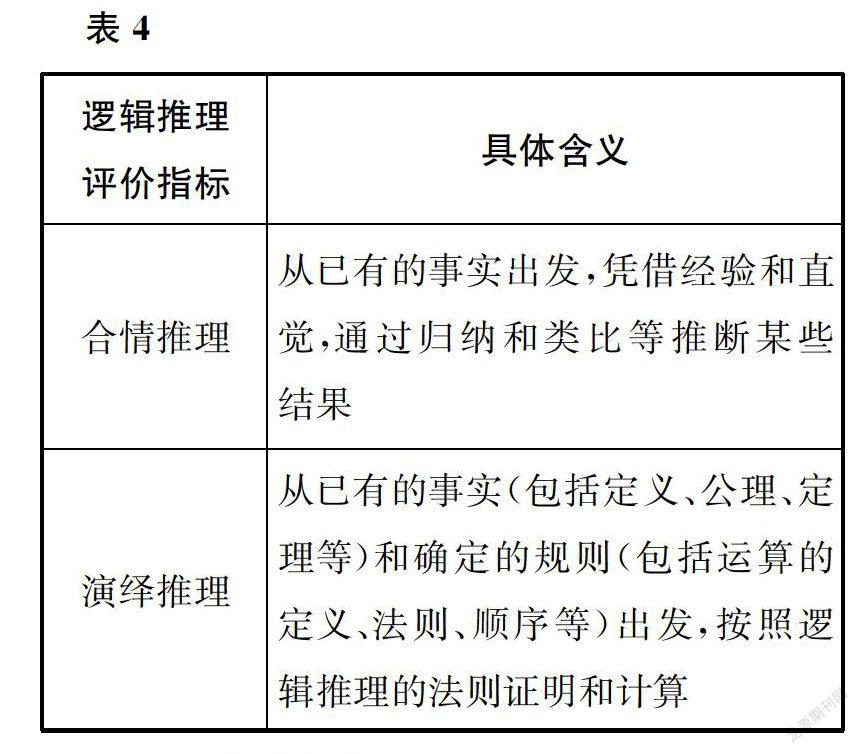
逻辑推理是指从定义、事实和确定的命题、规则出发，严格符合逻辑法则的推理方式。包括四个思维过程：发现、提出、验证和表达数学命题。主要有以下三类：归纳推理、类比推理和演绎推理。归纳推理和演绎推理反映了人们认识事物的两条思维途径，前者是从个别到一般，后者是从一般到个别。归纳推理与类比推理合称为合情推理，这就把数学推理分为演绎推理和合情推理两类，可将这两个类别作为数学推理的二级指标（如表4）。

（三）数学建模

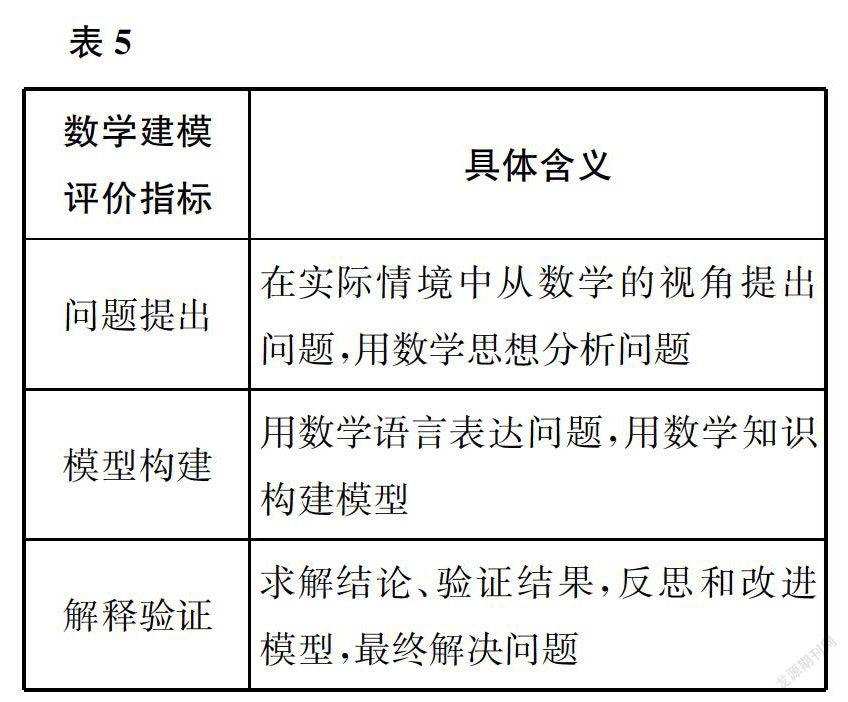
数学建模是根据相关的理论和方法来建立数学模型，并通过数学语言描述的方式来建立模型的一种方法。数学建模的过程一般包括以下几个步骤：模型准备、模型假设、模型建立、模型求解、模型分析、模型检验、模型应用。对上述七个阶段进行整合，可将问题提出、模型构建、解释验证作为数学建模的二级指标（如表5）。

（四）数学运算

数学运算包括根据概念、公式、法则等，寻求并设计合理的对数、式等的正确运算和变形;寻找简捷的运算途径;根据要求对数

据进行估计，分析条件，并进行正确运算。数学运算是解决数学问题的基本能力，是数学应用的基础。数学运算素养的发展，主要分为以下三个阶段：了解和理解运算、掌握和应用运算、综合和灵活运算。因此，可以构建数学运算的二级指标（如表6）。

（五）直观想象

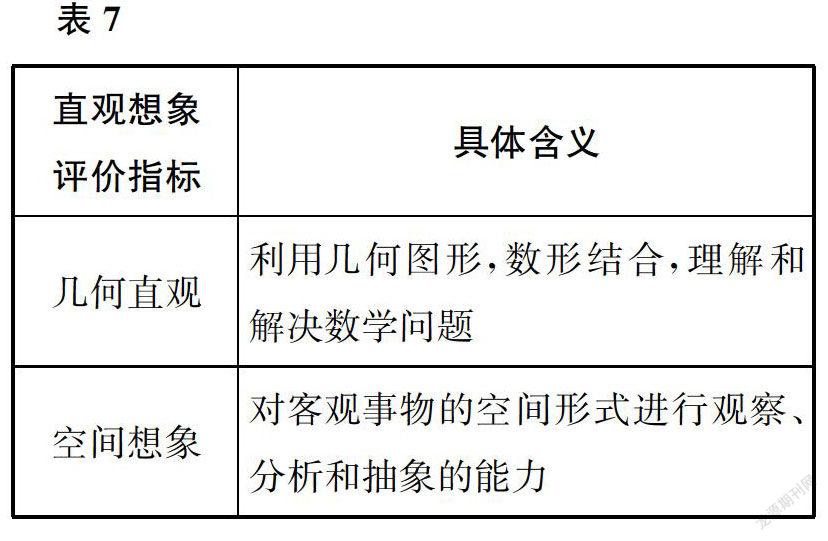
直观想象是指借助几何直观和空间想象感知事物的形态与变化。而几何直观主要是指利用图形解决数学问题，包括对图形的认识、把握图形之间的关系等;空间想象主要是指对空间几何体进行观察、分析、认知。几何直观与空间想象都是几何领域学习的必备素养，也都是逻辑性较强的素养：学生需要架构实物与其相应图形之间的逻辑关系。几何直观与空间想象是各有侧重的数学素养，也是各具指向的数学素养：几何直观重在“看”，空间想象重在“想”;几何直观重“直觉”，空间想象重“创造”。因此，可以构建直观想象的二级指标（如表7）。

（六）数据分析

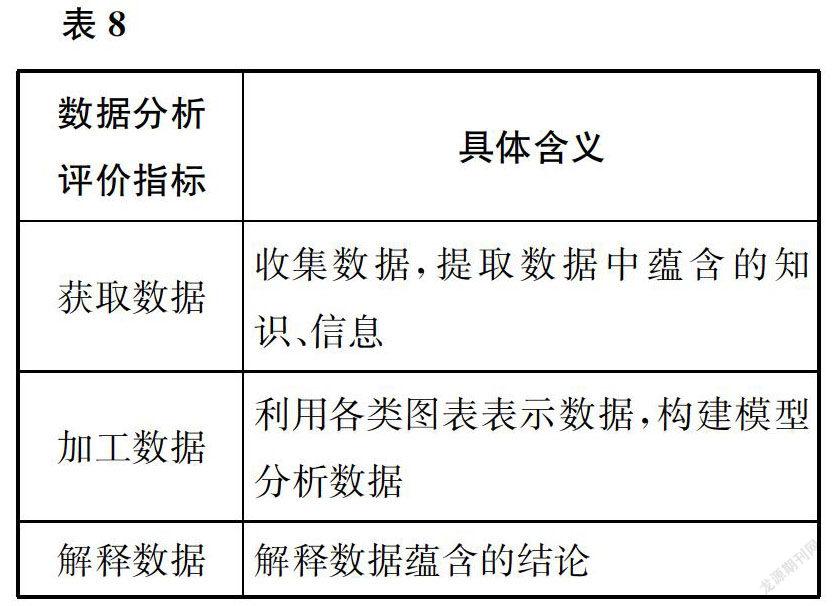
数据分析是指针对研究对象获得相关数据，运用统计方法对数据中的有用信息进行分析和推断，形成知识的过程。数据分析素养的培养，有利于学生获取有价值的信息，能够增强学生用数据表达现实问题的意识，能够形成通过数据认识事物的思维品质。数据分析的过程主要包括：收集、整理、理解、处理、获得、解释数据，并形成相应的数学知识。因此，可以构建数据分析的二级指标（如表8）。

三、研究反思

为什么要进行数学核心素养评价一级指标、二级指标的分类呢？主要有以下几点原因：其一，高中数学课程标准修订组提出的六大数学核心素养，很多学者对其评价指标的理解各有异同，无论哪种分类，都较难概括数学核心素养具体内容的全貌，那么，对其二级评价指标的分类，既可以较好地解读一级指标，又能够补充一级指标没有凸显的内容;其二，从国际数学课程、国际比较测试项目对数学素养的评价来看，评价指标的分类均深入至二级指标，甚至三级指标层面，有利于评价的可操作性;其三，二级指标是一级指标的分类或者是一级指标发展的过程性指标，所以两者评价的指向具有一致性。

值得说明的是，对于核心素养，我们更多地理解为一个整合了知识、技能、情感、态度与价值观等元素的集合体概念。因此，在数学核心素养的评价指标中，这里所列出的二级评价指标并不能够全部涵盖相关一级指标的所有内涵。例如：推理分为合情推理和演绎推理两类，其中合情推理分为归纳和类比两类;在数学运算中，除了考虑运算法则、运算策略之外，还有运算速度、运算精确性等。在数学核心素养评价指标体系中，仅选择占主体部分的二级指标作为评价内容。当然，所有二级指标的集合并不能等于一级指标。并且，对高中生数学核心素养评价指标的理论研究，还需要通过实证研究，去验证并调整该指标体系。

*本文系江苏省教育科学“十三五”规划课题“学科核心素养的内涵、测评与发展研究”（编号：Cc/2016/01/27）、江苏省教育厅“基于测试分析的跟进式改革重大研究项目”中“义务教育学科核心素养和关键能力研究”（编号：2015jyktzd02）和全国教育规划中小学数学教育研究重大招标课题“义务教育数学课程整体设计”（编号：GOA107001）的阶段性研究成果。参考文献：

[1] Ministry of Education，Ontario.The Ontario Curriculum Grades 11 and 12 （Mathematics）[M].Canada：Queen’s Printer for Ontario，2007.

[2] 香港课程发展议会.数学教育学习领域数学课程及评估指引（中四至中六）[M].香港：课程发展处，2007.

[3] Ministry of Education，Singapore[EB/OL]. http：//www.seab.gov.sg/syllabusSchool.Mathematics Higher1-3（syllabus）.pdf，04/02/2011.

[4] 王林全.英国学校数学课程的新发展[J].数学教学，2014（6）.

[5] 倪明，熊斌，夏海涵.俄罗斯高中课程改革的特色——数学课程普通教育与英才教育并举[J].数学教育学报，2010（5）.

[6] 徐斌艳.德国高中数学教育标准的特点及启示[J].课程·教材·教法，2015（5）.

[7] 廖运章，卢建川.澳大利亚高中数学课程进展及特点分析[J].课程·教材·教法，2014（6）.

[8] Curriculum and Assessment Policy Statement（CAPS）：Mathematical Literacy （Grades 10-12）[M].Republic of South Africa：Department of Basic Education，2012.

[9] 李艺，钟柏昌.谈“核心素养”[J].教育研究，2015（9）.

[10] 刘达，徐炜蓉，陈吉.基于PISA2012数学素养测评框架的试题设计一例[J].外国中小学教育，2014（1）.

[11] The Organization for Economic Co-operation and Development（OECD）.OECD Programme for International Student Assessment（PISA）[EB/OL].http：//www.oecd.org/pisa/aboutpisa.

[12]TIMSS 2011 International Results in Mathematics[EB/OL].http：//timss.bc.edu/timss2011/downloads/T11_IR_M_Executive_Summary.pdf.

[13] I.V.S.Mullis，M.O.Martin，P.Foy，A.Arora（2011），TIMSS 2011 International Results in Mathematics[EB/OL].[2012-12-12].http：//timssandpirls.bc.edu.

[14] 徐瑾劼.“Literacy”：PISA素养观背后的教育学立场[J].外国中小学教育，2012（1）.

[15] 喻平.数学学科核心素养要素析取的实证研究[J].数学教育学报，2016（6）.

[16] 洪燕君，周九诗，王尚志，鲍建生.《普通高中数学课程标准（修订稿）》的意见征詢——访谈张奠宙先生[J].数学教育学报，2015（3）.

[17] 史宁中.数学思想概论（第2辑）：图形与图形关系的抽象[M].长春：东北师范大学出版社，2008.

[18] 徐利治.数学与思维[M].大连：大连理工大学出版社，2008.

[19] 张胜利，孔凡哲.数学抽象在数学教学中的应用[J].教育探索，2012（1）.

[20] 顾沛.关于合情推理与逻辑推理的教学——以初中数学为例[J].中小学教材教学，2015（1）.

[21] ﹝美﹞G.波利亚.数学与猜想（第一卷）[M].李志尧，等，译.北京：科学出版社，2001.

[22] 黄弋钊.数学建模与学生能力培养探讨[J].时代教育，2015（5）.

[23] 徐亚培.新课标下初中数学建模教学方式初探[J].数理化解题研究，2007（6）.