小学数学中三角模型的建立与运用

孙勇 郑静

在《义务教育数学课程标准》中提到一个核心概念，就是模型思想。《课标》中所说的模型，强调模型的现实性，是用数学的语言讲述现实世界中的故事;强调在建立模型的过程中，让学生感悟如何用数学的语言和方法描述或者解决一类现实生活中的问题。模型是能够解决一类具有实际背景问题的数学方法。

在小学数学中，任何复杂的数学问题，都是由两个或多个简单的数量关系构成的。而任何一个简单的数量关系都由三个相关联的量组成，这三个相关联的量，它们之间有着一定逻辑关系。这种数量关系，我们就可以用一个三角形来反映，用三角形反映出来的数量关系可以让学生能直观、准确地认识和理解数量关系之间的内在联系和变化规律，并运用于实际学习中。而这个表示数量关系的三角形一但在学生的大脑里形成思维模型，对解决数学问题就会思路清晰、速度快捷、结果准确。

通过我们在小学一线多年的实验与观察，思考与实践，总结与验证，从而得出了一套简单完整易学的教学法——“巧用三角模形，解决数学问题”。在该教学方法中，我们将小学数学中一般数量关系、运算定律、计算公式、变化规律等都放在一个简单的三角模型中表述出来，从而加快、加深学生对数量关系、计算公式、运算定律、变化规律的认识、理解和运用，特别是解决数学问题中的数量关系的分析，解题方案的确定更是一目了然、方便准确。让我们的教学事办功倍，且效果显著。现将“巧用三角模形，解决数学问题”的基本应用原理总结如下：

一、三角模型的认识

在小学一年级数学《数的初步认识》教学中，我们把自然数进行分解与组成，以方便后面的加减法的计算，这种数的分解和组成，就可以构建一个三角模型。如：把8分解成5和（）（如图1所示）。把6和3合并成一个数是（）（如图2所示）。

用（8、5、3）这组数中的三个数写出不同两道加法和不同的两道减法。学生通过摆小棒、数数等方法写出了四个不同的算式。3+5=8，5+3=8，8-5=3，8-3=5。这三个数之间到底有什么内在关系呢？学生就很难说清楚。如果让学生把这三个数写在一个三角形上（如图1），就容易看清它们之间的内在联系了。两底角上的数之和等于顶角上的数，顶角上的数减去一个底角上的数等于另一底角上的数。

以上算式中的三个数是围绕三角形三个角上的数变化而来的，这样学生就容易理解这三个数的变化规律和内在联系了。学生通过三角模型，不仅可以轻易地写出不同的加减算式，并且也发现了加减互逆的关系。

我们把几个数的运算、计算规律或等量关系，用三角形的形式表示出来，并让学生在头脑里形成一种固定的模式，我们将它称作为三角模型。

二、三角模型的建立

为了在学生头脑中建起这种三角模型，方便以后的学习和运用，我们约定把三角形的顶角上标著固定的数量，如：（和或被减数;积或除数）（如：图3、图4、图5、图6），三角形两底角上写上相对应的其它两个量。

学生学会了建立并运用这种三角模型，为今后的学习带来了极大的方便。对归纳、总结所学的知识，以及知识间的各种联系及内在规律的认识极为有帮助。也为我们解决问题带来了方便，使我们看待问题会更直观，更容易发现其中的变化规律，也便于理解和记忆

三、三角模型在小学数学中的运用

现就对三角模型在小学数学教学中怎样解决一些教学难点和教学中的一些瓶颈问题作一简要概述

1、小学数学关于比多比少的一些实际问题。

很多低年级的小朋友总是把比多比少的问题弄不明白，总喜欢把比谁多的题用加法，比少的题用减法。对这类问题，如果学生弄清了比较量和被比较量的大小，按规律把各种数量准确地表示在三角模型上，就能正确地找到求未知数量的方法，并准确地求出这个数量。

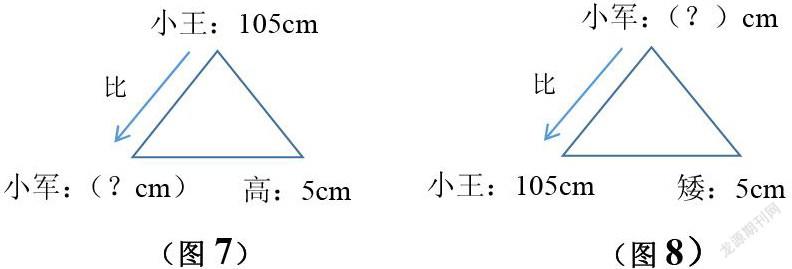
如：小王今年身高105厘米，比小军高5厘米，小军身高多少厘米？

小王比小军高，所以小王高，小军矮。根据三角模型的约定，应该把小王的身高写在三角模型的上顶角上，则把小军的身高写在底角左边，高5厘米写在三角形底角的右角上。从上到下逆时针方何把题目各量标在三角形的三个角上。（即上顶角、左下角、右下角）在三角模型上依次标上数后，根据三角模型的加减关系的计算规律，求小军的身高，写在三角模型的左下角，所以求左下角的数用减法计算，（如图7所示）。（求三角模型上顶角的数用加法，求三角模型下底角上的任意一个数都用减法）即105一5=100（厘米）

如果将上题改为：小王今年身高105厘米，比小军的身高矮5厘米，求小军的身高？则小军身高应比小王身高高，所以三角模型上的数量应发生变化，即小军的身高应写在三角模型的顶角上，小王身高和矮的5厘米依次写在左下角和右下角上，顺时针方向写出各个数量，（如图8所示）。求三角模型顶角上的数，用加法计算：105+5=110（厘米）。

在给三角形标数量时，“多几”或“少几”的数写在三角形的右下角，其他的量按“多”反时针方向，“少”顺时针方向地把数量写在三角模型上，求三角形上顶角的数用加减，求底角上的数用减法计算。这样学生在求比多比少的问题吋，只要能找到谁多谁少，就能正确地求出这三个量中的任何一个未知量了。

2、用三角模型解决乘除法应用题的一些问题

例如：有m千克花生榨了n千克花生油，请问（1）每千克花生能榨多少千克花生油？（2）榨一千克花生油需要多少千克花生？学生解决这类问题时，总是分不清谁做被除数、谁做除数，列式时总是弄错。如果我们用三角模型来分析这类问题就会清楚多了。首先我们要看所求的问题（1）是求每千克花生能榨多少千克花生油？我們把这个问题用这种形式写出来：“（？）千克花生油/千克花生”，根据三角模型的特点，我们把这个表示一份的数“（？）千克花生油/千克花生”写在三角形的左下角，根据每份数的书写格式就知道，应该是油的重量除以花生的重量。所以油的重量是总量，写在三角模型的顶角上，花生的重量是表示份数的多少，写在三角模型的右下角上。（如图9示）。

这是乘除关系，所以求每一份的量用（总量÷份数=每一份的量）因此式子是：花生油n千克÷花生m千克，即（n÷m）。

（2）每千克花生油需要多少千克花生？这个每份数应该写成：“（？）千克花生/千克花生油”（如图10所示）。根据每份数的书写格式就知道：应该是花生的重量除以油的重量。所以，三角模型的顶角上就应是花生的重量，三角模型的右下角应写份数→花生油的重量。根据问题求每千克花生油需要多少千克花生，应由顶角上的花生重量除以花生油的重量。即为（m÷n）。由于问题的不同，总量和份数也发生了变化，学生对这样的问题总是易把总量和份数混淆，通过三角模型，就能让学生正确区分总量与份数，从而找到正确的解题方法。

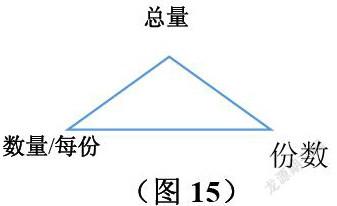
由于个别学生记忆差，理解问题的能力有限，如果我们将众多的公式用一个三角模型来表述，这样可以减少学生的记忆内容，提高学生的理解能力，从而提高学习效果。如我们把解决问题的众多公式如：速度×时间=路程、单价×数量=总价、工作效率×工作时间=工作总量、单产量×数量=总产量…（如图11、图12、图13、图14）

在这里，速度、单价、工作效率、单产量都表示总量中的1份，我们叫它是每份数。而时间、数量都表示每份数的多少，我们叫它为份数。结果都为总量。在三角模型（图15）上。这样表示每份数都用/的形式写一出来，分数线的上面分子的单位与总量的单位一致，分数线下面分母单位与份数的单位一致。这样就可以在三角模型上找出各部分的关系，而不用记太多的公式，还可避免题中单位不一致，造成的解题错误。

3、用三角模型解决小数乘除法中的小数点变化规律

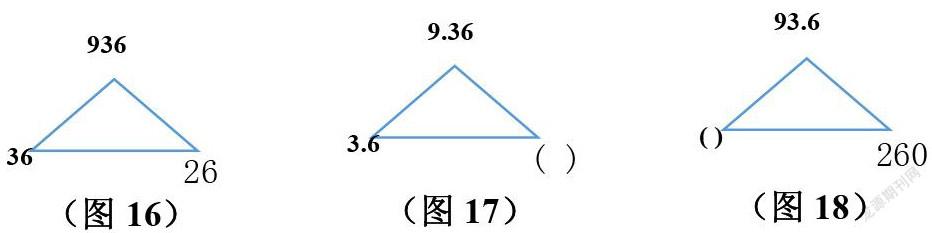
小数乘除法中，小数点变化的规律学生很难掌握，特别是三个数的小数点都有变化，学生就更摸不着头脑。比如根据936÷36=26（如图15）在下面的括号中填上适当的数：

936÷36=26 ①9.36÷3.6=（）②93.6÷（）=260

如图16、17所示，我们做第1题时，根据图16所示，三角模型上的三个数都是整数。而题①中的被除数和除数都是小数，且小数位数不同。因此我们看被除数从936变成9.36，缩小了100倍，而除数36变成3.6，只缩小了10倍。因此商也应缩小10倍。（即：三角形顶角上的数扩大或缩小的倍数与两底角上的数扩大或缩小的倍数之积相等）。再看题②：被除数从936变成93.6，缩小了10倍，而商由原来的26变成了260，扩大了10倍，除数会怎么变化呢？根据积商变化规律——三角形顶角上的数扩大或缩小的倍数与两底角上的数扩大或缩小的倍数之积相等。三角形顶角上的数缩小了10倍，商扩大了10倍，因此除数应缩小100倍，所以应是（0.36）.

4、用三角模型解方程

在数学教学解方程时，有许多种解方程的方法，如：利用等式的性质;利用加减乘除的等量关系等。用等式的性质解方程时，在遇到未知数是减数或除数时，解决起来就比较麻烦，要先将减数转换成加数，除数转换成因数再来解，学生还易出错，而利用等量关系式解方程时，学生要记住一系列的等量关系式，有个别学生记忆差，总把等量关系式用错，造成解方程错误。因此，利用三角模型来解方程，就显得简单方便。

根据三角模型的约定，我们把和、积、被减数、被除数定位在三角形的顶角上，其它对应的数量定位在三角形的两底角上，利用加减互逆、乘除互逆的特点来求解方程。

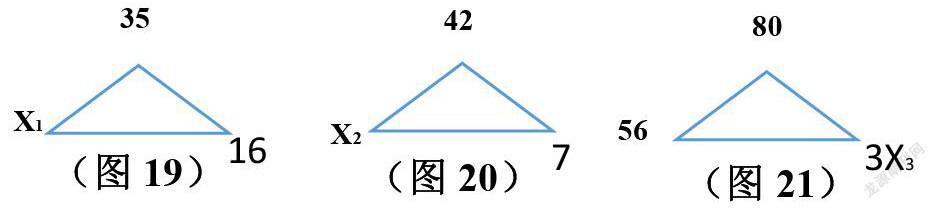
如：解方程①35-X1=16 ②42÷X2=7 ③56+3X3=80。

根據三角模型的约定，把方程的各个数量写在三角形的相对应的位置，根据加减互逆的特点：X1是减数，属于加减关系，所以X1=35-16，X1=19;X2是除数，属于乘除关系，所以X2=42÷7，X2=6;把3X3看作一个整体，即为加数，属于加减关系，所以3X3=80-56，3X3=24，X3=24÷3，X3=8。根据互逆的特点，解加减关系的方程时，求三角形顶角上的数时用加法计算、求三角形底角上的数时用减法计算、解乘除关系的方程时，求三角形顶角上的数用乘法计算，求三角形两底角上的数时，用除法计算。这样，学生就能更快、更准确地求出方程的解。

以上几个例子只是我们在教学中的部分实例，“巧用三角模形，解决数学问题”是我们在教学中多年的探索、实践总结出来的一套简单实用的帮助学生学习数学的方法，经过实践，教学效果显著。

指导老师：杨豫晖教授。

注明：本文受佛山科学技术学院大创项目支持，项目编号为：XJ2018264。