基于知识粒化的信息系统增量式属性约简

(四川文理学院 智能制造学院，四川 达州 635000)

属性约简是粗糙集理论[1]在机器学习和知识发现等领域中一种常用的数据处理工具，它通过对数据中冗余属性进行删除从而达到更好的分类性能。在现实的数据中，数据快速更新，每时每刻都有新的数加入，而传统的非增量式属性约简在求动态数据的约简集时需要进行大量的重复计算，这样消耗了大量的时间和空间，不能很好地满足实际的需求[2,3]。

增量式属性约简[2,3]相对于传统的属性约简，是一种专门针对动态数据集的约简方法，它能够在原先约简集的基础上进一步导出更新后数据集的约简，因而大大降低了时间的消耗[4]。在数据集的动态变化过程中，属性的不断增加是一种常见的形式[5]，对于这类数据集的动态属性约简，学者们提出了大量的方法，龙浩等[6]学者运用信息系统的差别矩阵，提出了当信息系统动态变化后的差别矩阵更新，并利用更新后的差别矩阵来进行增量式属性约简。葛浩等[7]学者也利用了差别矩阵构造出了类似的增量式属性约简算法。冯少荣等[8]学者通过改进的差别矩阵进一步构造增量式属性约简。吴晓瑛等[9]学者通过区分矩阵提出了一种维度增量的属性约简算法，景运革等[10]学者通过关系矩阵的增量更新也提出一种增量式属性约简，同时运用知识粒度的矩阵形式来进行属性约简[11]。可见，矩阵方法在增量式属性约简中占有很重要的地位，但是矩阵具有时间复杂度和空间复杂度高等缺点[9,11]，因而这些算法在计算效率方面具有一定的不足。

知识粒度是粒计算模型中评估信息系统知识粒化程度的一种度量方法，目前成功的运用于信息系统中不确定性度量、决策分析等领域[12-14]，同时也是构造信息系统属性约简的一种重要方法[15]，文献[15]证明了基于知识粒度具有较好的属性约简效果，然而这种属性约简方法是非增量式的，不能满足现实环境下动态数据的处理需求，因此本文在原来知识粒度属性约简的基础上，提出一种针对信息系统属性不断增加时的增量式属性约简算法。文中首先提出一种当信息系统属性增加时知识粒度的增量式计算方法，并证明这种计算方式可以大大减少重复计算，然后根据这种增量式计算提出一种增量式属性约简，所提出的增量式属性约简算法是在信息系统原先属性约简的结果上进行的进一步计算，避免了对已有数据的重复计算，提高了动态数据的处理效率，仿真实验结果表明了该算法在约简结果和时间效率方面都具有更好的性能。

1 基本理论

在属性约简中，数据集被描述成信息系统[1]的形式，一个信息系统可表示为IS=(U,A,V)，其中U为非空有限对象集，称为论域，A为非空有限属性集，V为属性集的值域，若属性集A=C∪D，且C∩D=φ，那么此信息又被称为决策信息系统，其中C,D被称为条件属性和决策属性。

对于属性子集B⊆A可以导出一个等价关系RB,其定义为

RB={(x,y)∈U|∀a∈B,a(x)=a(y)}

通过等价关系RB可以在论域U上诱导出一个划分U/RB={X1,X2,…,Xm}，简单表示为U/B，其中∀Xi∈(U/B)称为x关于B的等价类。

对于信息系统IS=(U,A,V)，设P,Q⊆A，由属性子集P诱导的划分为U/P={X1,X2,…,Xm}，Q诱导的划分为U/Q={Y1,Y2,…,Yn}，对于偏序关系满足(U/P)⪯(U/Q)当且仅当∀Xi∈(U/P)存在Yj∈(U/P)使得Xi⊆Yj，也可以称P比Q更精细。如果(U/P)⪯(U/Q)且(U/P)≠(U/Q)，称P比Q更严格精细，表示为(U/P)(U/Q)[12-14]。

定义1[12-13]：设信息系统IS=(U,A,V)，对于属性子集B⊆A导出的划分U/B={X1,X2,…,Xm}，那么信息系统基于B的知识粒度定义为

定义1所示的是知识粒度的基本定义，它描述了等价关系对整个知识空间粒化精细程度的一种评估，是粒计算理论中度量属性子集分类能力的一种重要方法[12-13]。

定义2[11]：对于信息系统IS=(U,A,V)，若B1,B2⊆A，那么B2关于B1的知识粒度定义为

GK(B2|B1)=GK(B1)-GK(B1∪B2)

定义2是从知识粒度的角度，用来度量信息系统中两个属性子集之间的关系程度，这种关系程度的度量为基于知识粒度的属性约简的提出提供了理论基础。

定义3[11]：设决策信息系统为DIS=(U,C∪D,V)，B⊆C是该信息系统的一个属性约简当且仅当

①GK(D|C)=GK(D|B)

② ∀a∈B,GK(D|B-{a})>GK(D|B)

根据定义3的属性约简定义，一种新的属性约简算法被提出[15]，具体如算法1[15]所示。

算法1 基于知识粒度的属性约简算法

整个算法1的属性约简过程可以通过图1所示的流程图来表示。其主要过程是通过知识粒度作为启发式函数，对属性进行启发式搜索，每次选择出属性重要度最大的属性添加入属性约简结果中，若剩余属性中最大的属性重要度为0，那么此时认为剩余的所有属性都是冗余的，则直接输出最终的属性约简结果。

2 知识粒度的增量式属性约简

2.1 知识粒度的增量式更新

由于现实数据集不断增量更新，传统的方法属性约简算法面临着时间和空间复杂度高的挑战[3]。

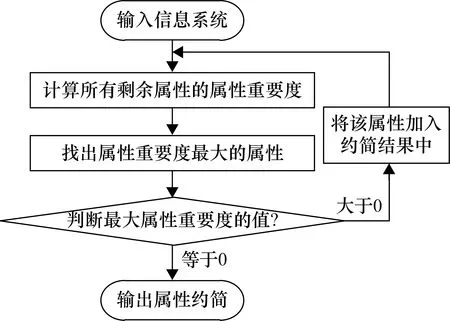
图1 算法1的流程图

Wang[5]等学者提出了一种信息熵的增量更新方法，对于属性不断增加的数据集，该方法在属性约简的过程中大大地减少了重复计算量，有着较高的约简效率，因此本文在此基础上，将该更新方法应用于知识粒度的增量计算中。

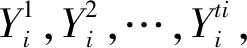
由于信息系统增加属性后，论域的划分逐渐变的更加精细，因此增加属性集ΔB后，那么就满足关系(U/B′)⪯(U/B)，并且信息系统增加属性后，会使得原先部分的等价类发生进一步的划分，因此将U/B′中的等价类分成两大类，第一类Φ表示的是未进行进一步划分的等价类，而Ψ表示的是U/B中进一步划分后的等价类。

由于信息系统的知识粒度与论域的划分直接相关，而增加属性集后，论域的划分逐渐变得越来越精细，根据知识粒度的变化关系，因此接下来将等价类的这种变化机制运用于知识粒度的增量更新。

定理1：对于信息系统IS=(U,A,V)，属性子集B⊆A在论域U上所诱导的划分为U/B={X1,X2,…,Xm}，属性子集B对应的知识粒度为GK(B)，当增加属性集ΔB后，令B′=B∪ΔB,设U/B′=Φ∪Ψ，其中Φ,Ψ同定义4，那么知识粒度GK(B′)满足

GK(B′)=GK(B)-Γ1

这里的

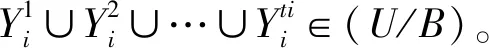
根据定义1知识粒度的定义有

对于上式中的通项

将Θi展开可以得到

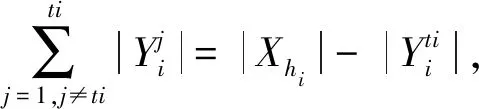
即

那么

由于

所以

即

GK(B′)=GK(B)-Γ1

其中

证毕。

定理1指出，当信息系统增加属性集后，知识粒度是逐渐减小的，并且减小的程度只与发生进一步划分的等价类有关，并且对于新的信息系统知识粒度，可以对进一步划分后的等价类进行相关计算就可以得到结果，这种增量计算方法可以避免重新对整个信息系统的论域进行划分计算，从而提高了计算效率。

在信息系统知识粒度增量式更新的基础上，将可以进一步推导出属性与属性之间知识粒度的增量更新，具体如定理2所示。

定理2：对于决策信息系统DIS=(U,C∪D,V)，对于B⊆C,B增加属性集后为B′,D关于B的知识粒度为GK(D|B),且U/B={X1,X2,…,Xm},同时U/B′=ΦB′∪ΨB′,U/(B′∪D)=ΦB′∪D∪ΨB′∪D。这里的

ΦB′={Xg1,Xg2,…,Xgp}

ΦB′∪D={Xg1,Xg2,…,Xgr}

那么知识粒度GK(D|B′)满足

GK(D|B′)=GK(D|B)-Γ2

这里的

证明：由定义2有

GK(D|B′)=GK(B′)-GK(B′∪D)

根据定理1可得到

GK(B′∪D)=GK(B∪D)-

所以

GK(D|B′)=GK(B′)-GK(B′∪D)

由于

GK(D|B)=GK(B)-GK(B∪D)

所以原式=GK(D|B)-Γ2，Γ2如定理2所示。

证毕。

随着属性的增加，论域划分逐渐变细，这里往往只有部分的等价类发生了变化。通过定理2可以看出，在已知原先知识粒度的情形下，增加属性集后，只需要对发生变化的等价类进行相关运算便可以得到新的知识粒度值，因而这样可以减少许多重复的计算，降低了时间的开销。基于这种变化机制，便可以构造出基于知识粒度的信息系统增量式属性约简算法。

2.2 增量式属性约简算法

令更新前的决策信息系统为DIS=(U,C∪D,V)，约简集为redC，知识粒度为GK(D|redC)。更新后的信息系统为DIS=(U,C′∪D,V)，新的约简集为redC′。那么信息系统属性增加后的知识粒度增量式属性约简如算法2所示。

算法2 增量式属性约简算法

整个算法2的运行过程可以通过图2所示的流程图来表示。当信息系统的属性发生增加后，算法2在原来属性约简结果的基础上，按照定理1和定理2所示的计算方法增量式计算知识粒度，然后观察新知识粒度与旧知识粒度之间值的关系，如果值不发生变化，说明原来的属性约简结果仍然可以作为新信息系统的属性约简，此时直接输出属性约简结果，若发生了变化，那么需要继续搜索属性，直到满足知识粒度相等时输出属性约简结果。正是由于增量式算法是在原来属性约简约简结果上进行的进一步计算，因此这样可以减少很多不必要的计算，提高了动态数据的处理效率。

对于算法2，设|C|=c，|C′|=c′，|U|=n，发生改变的等价类个数为l，那么算法1的时间复杂度为

O(c′2·n+(c′-c)·l)

3 仿真实验

在本节，将进行一系列实验来验证本文所提出算法的高效性和优越性。首先将本文所提出的知识粒度增量式属性约简算法与传统的知识粒度非增量式属性约简算法对同一组数据集进行处理，比较两类算法的属性约简效率，从而验证本文算法的高效性。然后将本文的增量式算法与其他相关的增量式算法进行对比，从而验证本文算法的优越性。

实验中所使用的公用数据集均从UCI中获取，详细信息如表1所示，其中Gas和Musk数据集为数值型的数据，因此在进行实验时需要进行离散化处理。由于本文所提出的是增量式属性约简算法，为了对表1中的数据集构造出动态变化的形式，本实验采用目前常用的构造方法[16-18]，将表1中每个数据集的属性全集大致分割成6个等份，选择第一份作为初始时的数据集，然后依次将剩余的属性子集加入数据集中，从而模拟出了属性集的5次动态增加。本文实验平台的硬件环境为CPU Intel core i3 6100 3.7 GHz和4 GB内存，操作系统为Windows 7旗舰版，实验所运用的编程工具为VC++6.0。

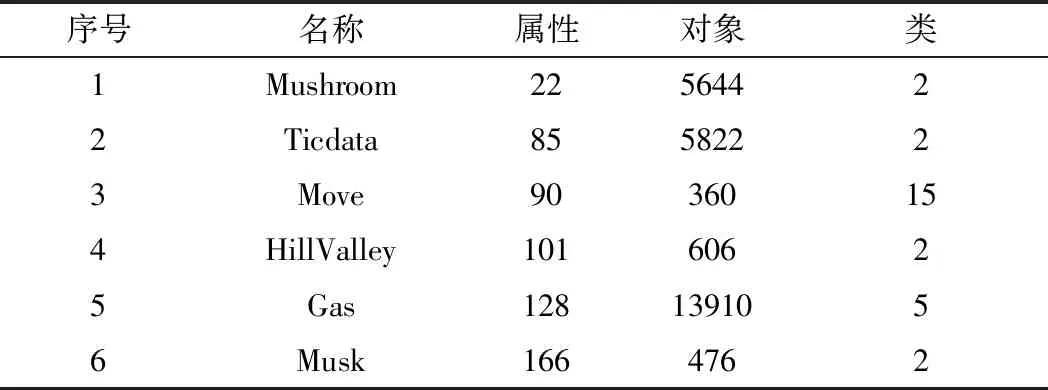
表1 UCI数据集信息

3.1 知识粒度的增量式与非增量式属性约简效率比较

图3所示的是每个数据集在知识粒度增量式和知识粒度非增量式两种算法中的属性约简时间效率对比图，其中横坐标表示属性的增量次数，纵坐标表示每次更新信息系统后属性约简所需要的时间。观察图3每个数据集的实验结果可以发现，在初始信息系统的属性约简时，两种算法的约简用时是一样的，这是由于增量式的属性约简算法刚开始时没有已知的结果信息，因此约简时采用的仍然是非增量式的属性约简算法。当信息系统更新后，两类算法的约简用时便出现了较大的差距，这主要是由于增量式属性约简算法的高效性，当信息系统属性增加时，信息系统中并不是所有的等价类都发生变化，新的知识粒度计算只对变化后的等价类进行计算，避免对未变化的等价类进行重复计算，而非增量式属性约简算法对未发生变化的等价类重复的计算了一遍，因而实验结果图中非增量式算法的所需时间要高于增量式算法的时间结果，部分数据集远高于增量式算法，例如Mushroom、Gas和Musk数据集。因此该部分实验结果表明本文所提出的增量式属性约简算法对属性动态增加的信息系统具有较高的属性约简性能。

图3 知识粒度的增量式和非增量式属性约简效率比较

3.2 其他增量式属性约简的比较

第一部分的实验结果表明了本文所提出的知识粒度增量式属性约简算法具有一定的高效性，接下来将进行优越性的验证实验，具体将通过对比目前已提出的增量式属性约简算法来比较。这些所对比的算法分别为：

① 基于区分矩阵的增量式属性约简，本实验记为算法A[9]；

② 基于属性概化的知识粒度增量式属性约简，本实验记为算法B[15]；

③ 基于属性增量的条件熵增量式属性约简，本实验记为算法C[5]；

④ 基于属性增量的联合熵增量式属性约简，本实验记为算法D[5]。

⑤ 记本文所提出的增量式属性约简为算法E。比较这些算法的增量式属性约简性能将通过约简集大小、约简集的分类精度以及增量式约简效率来体现。

3.2.1 各增量式属性约简算法的约简结果比较

表2所示的是5种增量式属性约简算法最终属性约简的结果比较。观察表2可以发现，本文所提出的增量式属性约简算法在大部分数据集中能够约简出更少的约简集，并且对于属性约简的平均结果，可以看出本文所提出的算法是最小的。

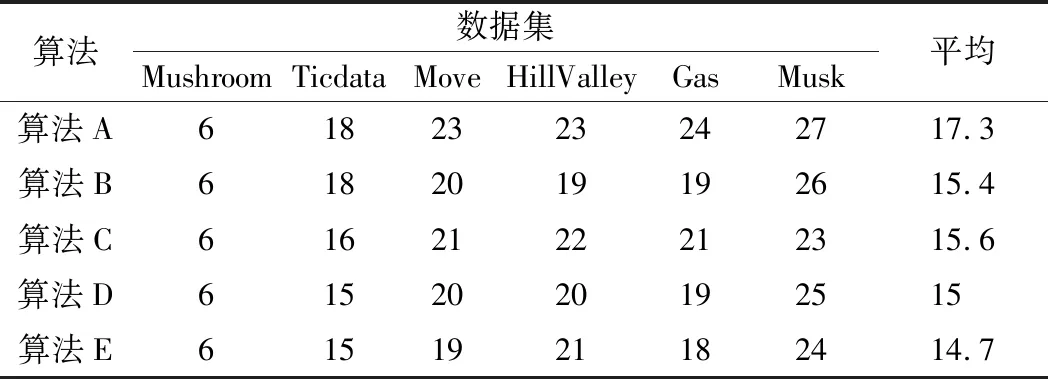
表2 增量式属性约简结果比较

表3和表4分别所示的是表2中属性约简结果在支持向量机(SVM)和改进决策树(C4.5)两种分类器下的分类精度结果。观察两个表可以发现，虽然本文所提出的算法不是在所有的数据集上都拥有最优的结果，但是本文算法所得到分类精度的平均值是最高的，例如表3所示的SVM分类精度中，本文算法在各个数据集上分类精度的平均值为0.8356，表4所示的C4.5分类精度中，本文算法在各个数据集上分类精度的平均值为0.8428，这两个结果均最高，因此可以看出本文所提出的算法在整体上具有更高的属性约简性能。

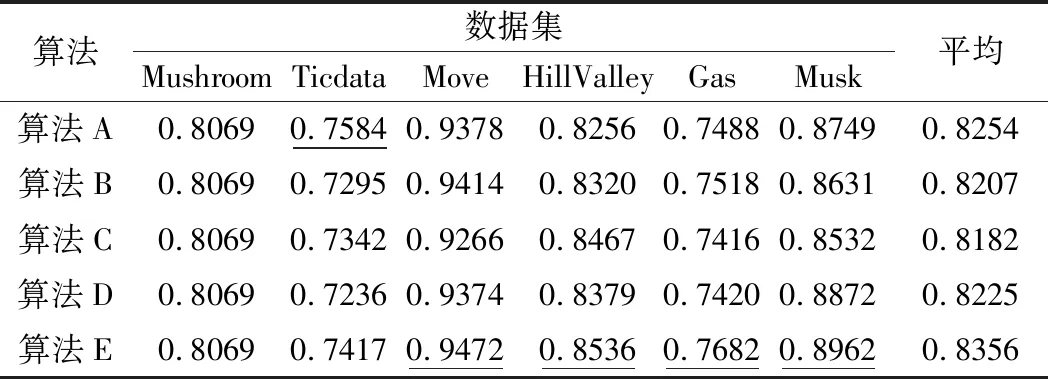
表3 SVM分类精度比较

表4 C4.5分类精度比较

3.2.2 各增量式属性约简算法的约简效率比较

图4所示的是这5种增量式属性约简算法在各个数据集下增量式属性约简的用时比较。观察图4的每个子图可以发现，随着属性更新的次数不断增加，这5种算法有着不同大小的属性约简时间消耗和不同的时间增长速率，算法A的时间消耗最多，这主要是由于算法是基于矩阵方法的增量式属性约简，运用矩阵在进行增量式计算时会产生更多的时间开销。其次时间开销较多的是算法C和算法D，这主要是由于这两种算法是基于熵模型构造出的增量计算，熵模型的计算具有较高的时间复杂度。最低的时间开销是算法B和本文所提出的算法E，他们都是基于知识粒度构造出的属性约简，知识粒度的计算方式比较简单，时间复杂度低，并且本文所提出的算法E是基于等价类变化的视角来进行增量计算，这种计算方法避免了等价类中不必要的重复计算，最大限度的减小了知识粒度的计算复杂程度，因而算法E具有更低的增量式约简时耗。

综合两部分的实验结果分析可以看出，本文所提出的增量式属性约简算法具有较高的属性约简效率，并且相比较其它算法更具优越，应用于属性增加的信息系统的增量式属性约简是适用的。

4 结束语

现实中很多数据的属性是不断动态增加的，如何对其进行增量式属性约简是目前知识发现领域研究的重点。本文在等价关系诱导划分的基础上，研究了当属性增加时知识粒度的变化机制，并基于此提出了一种高效的增量式属性约简算法，仿真实验结果表明，该算法相比较于目前同类型的算法具有更好的优越性。由于本文所提出的算法基于等价关系构建，因此接下来将探索数值型以及混合型数据的增量式属性约简方法。

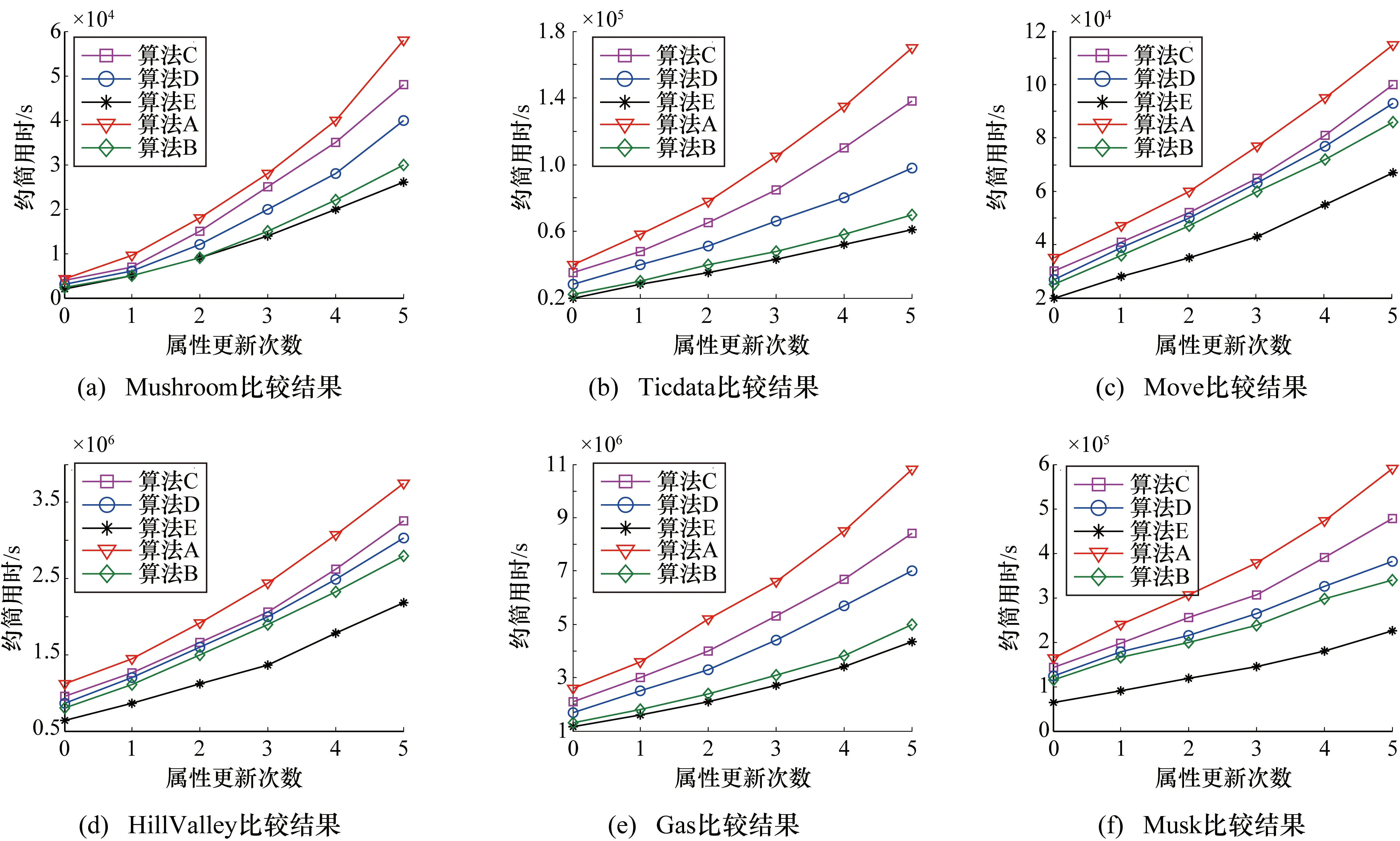
图4 5种增量式属性约简算法的时间比较