DNAN基熔铸炸药的慢烤相变及传热特性

王 帅，智小琦，王 雪，周 捷

(中北大学机电工程学院，山西 太原 030051)

引 言

熔铸炸药是当前应用最为广泛的一类军用混合炸药[1-3]，其在贮存、运输和使用过程中经常会受到不同程度的热刺激，对安全性造成了很大的威胁，因此对其热安全性的研究尤为重要。与其他类型炸药相比，在研究熔铸炸药的慢烤特性时，除了需要研究其点火温度、点火时间、点火区域和响应等级外，还应该研究其受热刺激后的相变情况及传热机理。Scholets等[4]研究了TNT炸药慢烤过程中的温度变化和分布情况，得到了炸药熔化对热反应的影响规律；王红星等[5]研究了2，4-二硝基苯甲醚(DNAN)炸药慢烤的自发火温度、热爆炸延滞期和热爆炸临界温度；McCallen等[6]研究了TNT在液态时的自然对流；陈朗等[7-8]建立了TNT和DANA炸药熔化、自热反应、热传导和对流传热的四分之一模型，计算标定了DNAN和TNT的反应动力学参数。

上述研究均为对纯TNT和DNAN熔铸炸药的研究，而对DNAN基熔铸炸药慢烤的研究较少。为了进一步研究DNAN基熔铸炸药慢烤相变及传热特性，本实验对尺寸为Φ30mm×60mm的DNAN基熔铸炸药的慢烤特性进行了研究并监测其中温度的变化。同时，采用CFD数值模拟软件FLUENT对尺寸Φ30mm×60mm的DNAN基熔铸炸药进行二分之一模型和全模型模拟计算的对比分析，以获得DNAN基熔铸炸药相变规律及传热特性，为DNAN基熔铸炸药的安全使用提供技术支持。

1 实 验

1.1 样品及仪器

慢烤样品药柱为DNAN基熔铸炸药，配方(质量分数)为：DNAN，31.6%；Al，25%；RDX，41%；添加剂，2.4%。药柱尺寸为Φ30mm×60mm，密度为1.80g/cm3，采用铸装工艺制备。

慢烤炉，自制；MR13温控仪，调节精度0.1K，杭州邦硕电子有限公司；K型热电偶，精度0.004K，北京航科金星自动化仪表有限公司。

1.2 慢烤实验装置及原理

实验装置如图1所示。

图1 慢烤实验装置Fig.1 Slow cook-off test device

慢烤炉、温控仪和热电偶构成温度反馈调节系统，输入既定的参数，温控仪控制慢烤样品壳体外壁按预定的升温速率升温。同时，温控仪实时采集实验过程中各监测点的温度，并将温度反馈给计算机，计算机实时显示各监测点温度—时间历程曲线。

实验所用慢烤样品由壳体、药柱和上下端盖3部分组成，端盖与壳体之间用螺纹连接，壳体材料为45#钢，壁厚3mm、端盖厚3mm。装配好热电偶的慢速烤燃弹如图2所示。

图2 装配好热电偶的慢速烤燃弹Fig.2 Slow cook-off sample fitted with thermocouples

采用多点测温方法，用3支K型热电偶测量温度：其中第一支固定在慢烤样品外壁(测点1);第二支埋在药柱中心处(测点2)；第三支埋在水平距药柱中心6mm处(测点3)。慢烤样品测温点位置示意图如图3所示。

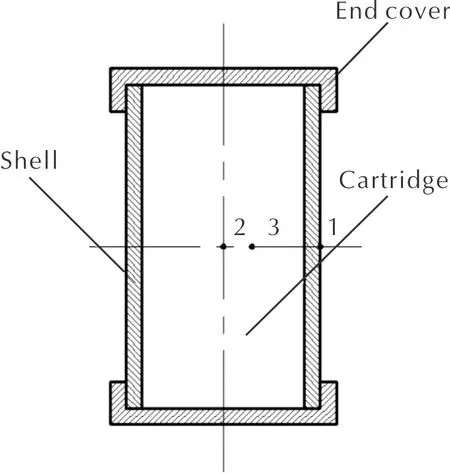
图3 测温点位置Fig.3 Locations of temperature measuring points

1.3 实验方法

从20℃(293.15K)开始加热，先按0.2K/min的升温速率加热至120℃，再按0.055K/min(3.3K/h)的升温速率对DNAN基炸药加热，直至实验样品发生响应。共进行两发平行实验，记录慢烤过程中各个监测点的温度—时间历程曲线，回收破片并通过炸药响应后壳体的破坏程度来确定响应等级。

2 结果与讨论

慢烤实验结果如表1所示，各监测点的温度—时间历程曲线和炸药响应后的壳体破坏程度分别如图4和图5所示。

表1 慢烤实验结果Table 1 Experimental results of slow cook-off tests

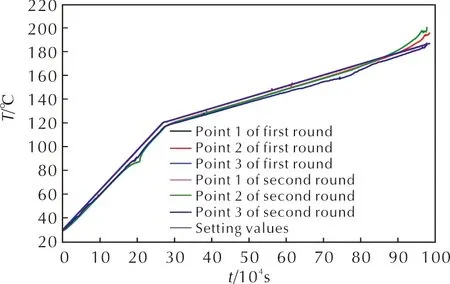
图4 实验监测点温度—时间历程曲线Fig.4 Measured temperature—time curves of temperature measuring points

从图4可以看出，在以0.2K/min的升温速率加热阶段，两发慢速烤燃弹监测点2、3的温度—时间历程曲线出现了温度上升变缓的一个阶段，之后又按既定的升温速率进行升温。这是由于炸药在熔化过程中由固态变为液态时吸收了部分热量导致升温变缓而引起的，可以判断DNAN基熔铸炸药在这个阶段发生了相变，从温度—时间曲线可以得到相变开始温度和相变终止温度。在响应阶段，由于炸药自身热分解作用，炸药内部温度非线性急剧上升，此时温度—时间历程曲线出现明显拐点，判断此时炸药发生响应。

图5 慢烤样品响应状态Fig.5 Response state of slow cook-off samples

从图5可以看出，炸药响应后，两发慢速烤燃弹壳体只发生了微小变形，端盖受剪切冲开，发生卷曲变形，壳体内部和端盖上均有白色的炸药反应产物。因此，确定慢烤样品发生了燃烧反应。

由于实验条件的限制，实验过程中只能通过温度—时间历程曲线得到DNAN基熔铸炸药各监测点的相变开始温度和相变结束温度；通过壳体的破坏程度判断DNAN基熔铸炸药的响应等级，而无法观察DNAN基熔铸炸药的相变过程、响应阶段温度分布情况、相变最终位置、点火点位置及点火温度等信息，为此采用数值模拟方法对实验进行补充。

3 数值模拟

3.1 数学模型的建立

DNAN基炸药慢烤质量、动量和能量的输运方程都可以用下面的通用形式表示[9]：

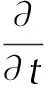
(1)

式中：φ为通用变量，代表质量、动量、能量等；ρ为流体密度；Γ为广义扩散系数；t为时间；S为炸药自热反应源项。

DNAN基熔铸炸药的自热反应遵循Arrhenius定律[10]，其自热反应源项为：

S=ρ·Q·A·exp(-E/RT)·f(α)

(2)

DNAN基熔铸炸药的Frank-Kamenetski零级反应方程为：

(3)

3.2 物理模型的建立

以慢烤样品实物图为参考，忽略壳体与端盖的螺纹连接，建立物理模型。为分析熔铸炸药相变及点火时是否结构对称，分别建立二分之一和全模型进行对比模拟。为提高网格质量，增加计算精度，采用SOLID六面体实体单元，网格尺寸0.25mm。慢烤样品的坐标系建立在壳体底面几何中心，有限元模型如图6所示。

图6 二分之一模型和全模型Fig.6 1/2 Model and full model

数值模拟计算过程中将壳体外壁设为壁面边界条件，调用C语言编写的UDF热刺激强度函数(UDF T -wall -new)，使壳体外壁面按既定的热刺激强度进行升温；壳体内壁面和药柱外壁面设为耦合边界条件；药柱区域设为流体，并调用UDF自热反应函数(cell_source_new)，药柱受热时将按自热反应函数规律进行反应。

对于DNAN基熔铸炸药的相变，FLUENT软件采用焓-孔隙率方法处理炸药的相变过程[11]。FLUENT中的相变过程引入液相率的概念，它可以间接表示固液相界面的位置。液相率可表示为：

(4)

式中:Ts和Tl分别表示材料的凝固温度和熔化温度，Ts=Tl时，相变过程只有液相和固相之分。当0<β<1时，认为相变材料处于固液糊状区，按多孔介质来处理，多孔部分等于液体所占份额。

炸药装药密度由实际称量并计算得到，其他材料参数参照文献[12]，得到DNAN基熔铸炸药组分物性参数如表2所示。

表2 DNAN基熔铸炸药组分物性参数Table 2 Physical parameters of components in DNAN based melt-cast explosive

参照文献[13]，再以实验所得监测点温度为依据，调整材料参数，直至实验结果与数值模拟计算结果基本吻合。调整后的DNAN基炸药的化学反应动力学参数活化能E=172kJ/mol，指前因子Z=1.2×1011s-1，反应热Q=4920kJ/kg-1。

3.3 数值模拟结果及分析

3.3.1 数值模拟与实验结果对比分析

参照实验建立相对应的计算模型和监测点，记录计算过程中的温度变化。表3为DNAN基熔铸混合炸药实验和数值模拟结果。

表3 慢烤实验和数值模拟结果的对比Table 3 Comparison of slow cook-off test and numerical simulation

从表3可以看出，各项数据误差都在5%以内，表明计算模型和相关参数能够描述该炸药的相变和自热反应。

图7为炸药各监测点实验和模拟计算温度—时间曲线对比。从图7中可以看出，对于炸药中心处，在炸药熔化前、熔化过程中和熔化后，以及在炸药点火反应阶段，模拟计算温度和实验测量的温度都能够很好地吻合，说明该反应模型和计算方法能够准确描述DNAN 炸药固-液相变和热分解反应过程。

图7 实验和数值模拟监测点温度—时间历程曲线Fig.7 Temperature—time curves of measuring points by experimental and numerical simulation

3.3.2 二分之一与全模型相变过程数值模拟与分析

为了更深入了解DNAN基熔铸炸药慢烤过程中的相变及传热特性，对Φ30mm×60mm规格的DNAN基熔铸炸药进行了二分之一和全模型的数值模拟与分析比较，从而得出DNAN基熔铸炸药的相变特征和传热机理，截取二分之一XOY平面和全模型XOY平面相变过程中对应相同时刻的液相分数云图，分别如图8和图9所示。

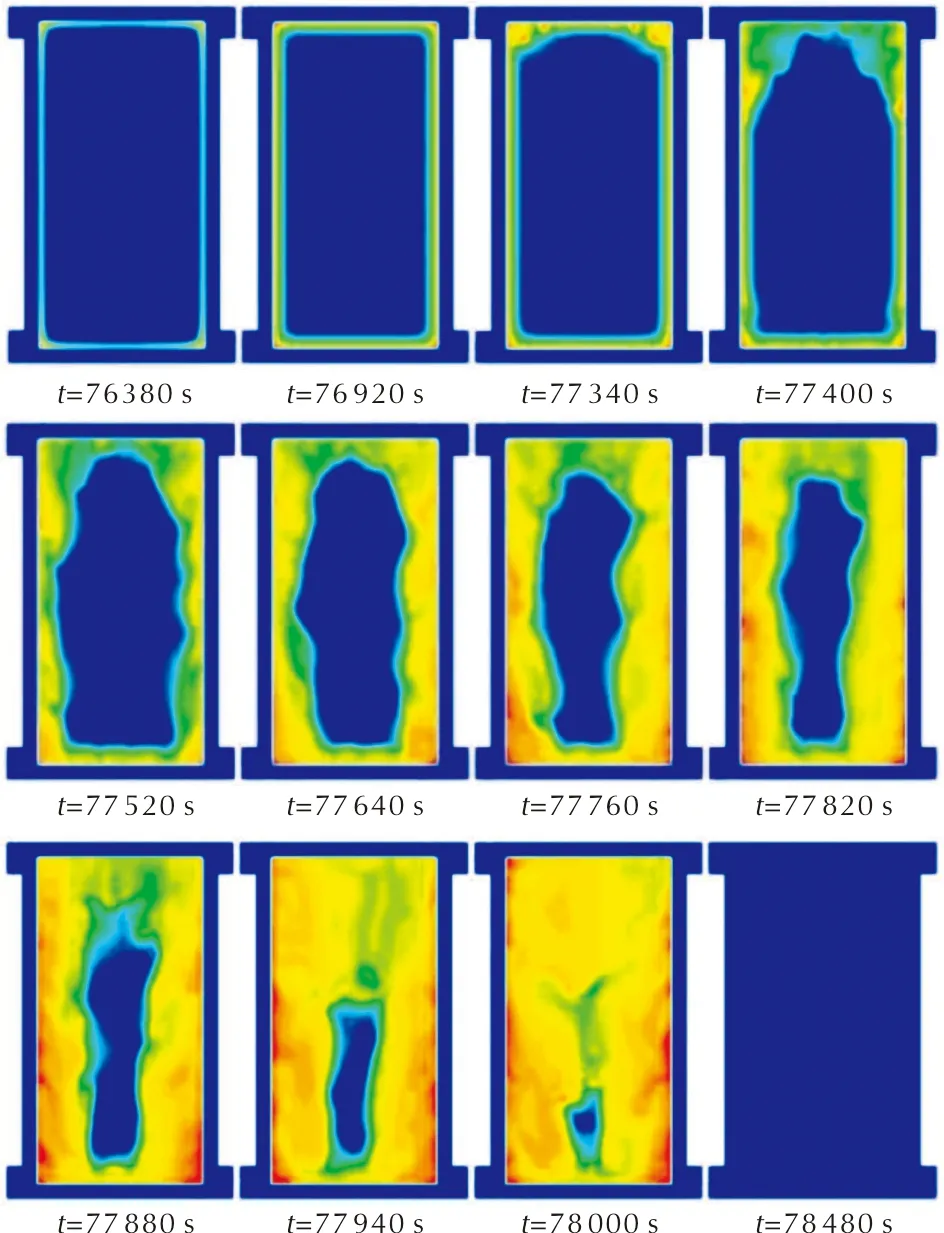
图8 二分之一模型XOY平面液相分数云图Fig.8 Liquid fraction distribution on XOY plane by 1/2 model

图9 全模型XOY平面液相分数云图Fig.9 Liquid fraction distribution on XOY plane by whole model

由图8和图9可知，DNAN基熔铸炸药中的DNAN在慢烤过程中发生相变，在相变的初始阶段呈对称分布，随着相变的进行逐渐呈现不对称分布，且二分之一和全模型的数值模拟结果并不完全一致，故在DNAN基熔铸炸药数值模拟中，二分之一模型不能准确反映其相变及传热过程，应该采用全模型。

参考图9分析DNAN基熔铸炸药的相变过程及传热机理：76380s时，在外热源的作用下，DNAN基熔铸炸药中的DNAN开始熔化，炸药从接近壳体附近开始熔化且呈对称分布，此时热量传递的方式有热传导和热辐射。但是，由于温度较低，热传导是主要的热传递方式，钢壳体的导热系数远大于DNAN基熔铸炸药，热量来不及进入到药柱内部，只有壳体附近的炸药发生熔化；77520s时，熔化区域逐渐扩大且开始呈现不对称分布，此时传热方式有热传导和热辐射。但是，随着相变区域的增大，温度分布不均导致炸药密度分布不均，液相的DNAN基熔铸炸药开始发生自然对流，此时对流传热成为热量传递的主要方式，重力作用和浮升力作用相当，固态炸药并未发生明显下沉；77940s时，绝大多数DNAN已经熔化，固态炸药的密度大于液态炸药的密度，加上重力作用大于浮力作用，固态炸药发生了下沉；78480s时，DNAN基熔铸炸药中的DNAN已经完全熔化，相变结束。

为了进一步探究DNAN基熔铸炸药相变速率的规律，根据数值模拟结果绘制液相分数随时间变化的曲线，如图10所示。

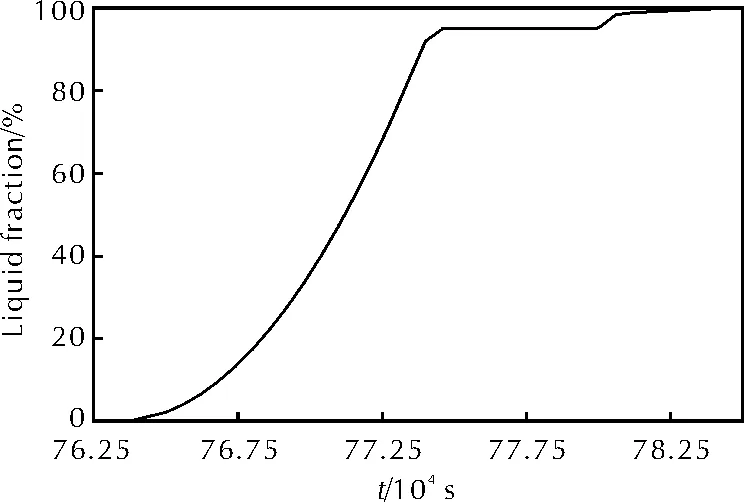
图10 DNAN基熔铸炸药相变过程中液相分数—时间历程曲线Fig.10 Liquid fraction time curves of DNAN based melt—cast explosive in phase transition

从图10可知，DNAN基熔铸炸药从开始发生相变到相变结束，相变速率经历了快速、速率为零、中速和低速4个阶段，这是炸药相变过程中导热系数和密度减小导致主要传热方式由热传导转变为对流传热引起的。

3.3.3 点火时刻数值模拟与分析

在DNAN基炸药慢烤过程中只能获得炸药的响应时间和响应等级，而对于炸药点火位置和点火温度无法获得。数值模拟中炸药温度的分布状态可以看出炸药的点火位置， DNAN基熔铸炸药全模型XOY平面不同时刻的温度分布云图如图11所示。

图11 DNAN基熔铸炸药慢烤温度云图Fig.11 Temperature distribution of DNAN based melt-cast explosive in slow cook-off process

从图11可知，在76380s前，DNAN基熔铸炸药中的DNAN尚未发生相变，热量由外向内传递。因此，内部温度低于外部温度，且呈对称分布；76380～78480s时间段是DNAN基熔铸炸药中的DNAN相变过程，相变从药柱外部向内部进行，药柱内部温度仍低于外部温度，加之固态炸药下沉和对流传热作用，导致低温区域向药柱底部移动且呈不对称分布。在78480s时，DNAN基熔铸炸药中的DNAN完全熔化，没有固态炸药吸热，炸药内部温差减小，对流作用减弱，因此此时温度基本呈对称分布；从130800s开始，炸药从药柱上部发生自热反应，此时自热反应不剧烈，放出的热量较少，药柱的温差比较小，对流作用弱，因此温度基本呈对称分布，随着自热反应的快速进行，药柱的温差变大，对流作用变强，药柱温度呈不对称分布，到209100s时，自热反应区域温度急剧上升达到炸药的点火温度，炸药在顶部靠近边缘处发生点火，此时点火位置温度约为203.8℃。

4 结 论

(1)由实验结果可知：DNAN基熔铸炸药中的DNAN相变开始温度约为81.8℃，相变结束温度约为95.3℃，响应等级为燃烧反应。

(2)由数值模拟结果可知：DNAN基熔铸炸药竖直放置时点火位置在药柱顶部靠近边缘处，点火温度约为203.8℃；慢烤相变过程中主要传热方式由热传导转变为对流传热导致相变区域的不对称分布，二分之一模型不能准确反映其相变及传热过程。因此，在数值模拟中，应采用全模型；慢烤相变过程中DNAN的密度和导热系数减小，从而导致从开始发生相变到相变结束，相变速率经历了快速、速率为零、中速和低速4个阶段。