数学核心素养在课堂教学中的落实

罗奕站

【摘  要】随着课改的不断深入，教师越来越关注学生学科核心素养的培养。就数学学科而言，核心素养归根结底是要学会用数学的眼光观察世界，用数学的思维分析世界，用数学语言表达世界。简单来讲就是教师在讲授某个知识点的教学过程中，课堂教学聚焦数学学科特点，发展运算能力、推理能力、空间观念及几何直观、推理能力、应用意识和创新意识等数学核心素养，关注学生完成某个知识概念的理解与建构以及应用，从而培养学生知识迁移和再学习的能力。那么，我们的学校教育如何落实学生在课堂学习中获取数学核心素养的能力，这种比“学会多少知识”更为重要。

【关键词】数学;核心素养;课堂教学

初中几何教学中，“探索全等三角形条件（1）”是个重要的知识点，其中蕴含丰富的数学思想，也是培养数学核心素养较好的教学素材。“探索全等三角形条件（1）”是在学习了三角形的有关概念（内角、外角、中线、高、角平分线），以及三角形三边之间的关系、图形的全等和全等三角形特征的基础上，进一步“探索三角形全等条件”中的“边边边” 和三角形的稳定性。它与前面学习的全等三角形的特征及后面将要学习的三角形全等的（“ASA”“AAS”“SAS”）判别方法作为探索三角形全等的核心内容。

学好第一节课内容的“分类探索方法和规范的几何语言表述”将为下节课探索其他条件打下坚实的基础，同时为今后探索直角三角形全等的条件以及探索三角形相似的条件提供很好的模式和方法。本文以这一节课为例，浅谈如何让数学核心素养落实到课堂教学中。

一、情景创设现主题，知识冲突引思维

弗朗西斯培根说：“知识是一种快乐，而好奇则是知识的萌芽。” 情境创设唤起旧知识的回顾，激发学生的认知冲突，从学生的“最近发展区”转化为“现要发展水平”，提高教学活动的针对性和有效性，培养学生创新意识。

教学片段1：引入环节

①已知，如图，△ABC≌△A′B′C′，则对应角： ∠A=————、∠B=————、∠C=————。

对应边：AB=————、BC=————、AC=————。

②判定两个三角形全等，根据全等三角形的定义必须满足（     ）。

（A）三边对应相等

（B）三角对应相等

（C）三边对应相等和三角对应相等

（D）不能确定

提出问题：判定两个三角形全等一定需要六个条件吗？条件能少吗？

根据学生已有知识“生长点”提出判定两个三角形全等一定需要六个条件吗？条件能少吗？”激发学习的兴趣，引发知识冲突，从而引入课题“探索三角形全等的条件”。

教师对学生的回答应有预判：第一种学生回答不能少;第二种学生回答可以少。教师要有教育智慧巧妙地应对，对第一种教师应“求异”，以“我觉得可以更少的条件就能判断两三角形全等”从而引发知识冲突;对第二种教师应“求同”，以“少什么条件能判断两三角形全等”从而引发知识冲突，让学生积极思考。

通过简单的数学问题，运用所学的数学知识、技能和基本思想进行独立思考，归纳概括得到猜想和规律，并加以验证。

二、动手验证悟方法，直观探究提素养

学生的核心素养是在问题解决的过程中慢慢养成的，问题探究的过程是培养素养的关键点。在合作动手验证的过程中逐步培养学生分析问题和抓住数学本质的能力，有助于形成有效的验证方法，然后通过画图、观察、比较、推理、交流等直观探究提升素养。

教学片段2：合作提升

活动1画一画：按照下面给出的一个条件各画出一个三角形。（几何画板展示）

①三角形的一个角为 60°。

②三角形的一条边长是3cm。

比一比：同一条件下作出的三角形与其他同学作的比一比，是否全等。

活动2画一画：按照下面给出的两个条件各画出一个三角形。（几何画板展示）

①三角形的两个角分别是：30°，50° 。

②三角形的两条边分别是：3cm，5cm。

③三角形一条边为3cm，一个角为 60°。

活动3画一画：按照下面给出的三个条件各画出一个三角形。

①三角形的三个角角分别是：40°，60°80。

②在硬纸板上画出三条边分别是 10cm，13cm，15cm 的三角形。

剪一剪：用剪刀剪下畫出的三角形。

比一比：作出三角形与其他同学作的比一比，是否全等。

基于学生的作图能力较弱，教师则必须引导学生抓住“作一角等于已知角”，只能定一个顶点和“作一线段等于已知线段”，确定两个顶点的数学本质，充分利用两个基本作图方法，搭建探索三角形顶点确定的方法的平台，给予小组充分地时间完成画一画、比一比，体会合作带来的成功体验。它符合课标指出“教材编写不是单纯的知识介绍，学生学习也不是单纯地模仿、练习和记忆，设计必要的数学活动，让学生通过观察、实验、猜测、推理、交流、反思等，感悟知识的形成和应用。

三、提炼方法重归纳，解题应用能力强

有效的课堂小结不是简单的“影片回放”，学生需要知识系统的重建和突破，做好方法提炼、思想内化，让核心素养生根发芽是教师义不容辞的责任。本节课的小结体现了三个层次，基础环节的小结注重知识整理，探索环节的小结偏向探索方法的提炼，最后小结着力在解题应用方法的渗透。

教学片段3：归纳小结

①而三边对应相等的两个三角形全等，简写为“边边边”或“SSS”。

培养学生归纳总结及语言表达能力，深刻体会“边边边”判定方法中文字语言，图形语言、几何语言的三种语言关系，为今后学习提供书写模式。

②分类探索方法一般步骤是：少、弱→多、强，培养分类探索的一般模式为后续学习服务。

③通过练习，引导学生分析题目中“有什么”的条件，并把题目的条件转化成特殊的符号融汇到图形中，使学生看到标有特殊符号的图形就知道有什么条件和问题，分析图形依照结论和定理寻找“缺什么”条件，这样目标指向才明确，思考问题思路才会清晰，然后“证缺什么”，这样提供了说明问题的基本模式。

教学片段4：课堂延展

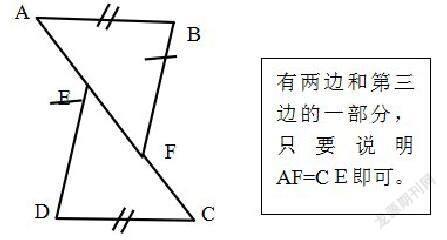
已知：如图，在△ABF和△ DCE中，AB=DC，AE=CF，BF=DE， △ABF与△ DCE全等吗？为什么？

四、结语

只有这样才能“引导发展”思维，使学生初步学会如何读题，并把题目的条件转化成特殊的符号融汇到图形中，根据图形的标志，知道“有什么”“缺什么”明晰问题说明的线索，为学生能规范地写出几何语言，说明问题提供了保障，同时也培养学生逻辑推理能力，为今后学习其他几何证明思路奠定基础。这样的设计也体现“数学教学不仅仅是数学知识的教学，更重要是发展学生数学思维的教学”。让我们一起关注数学核心素养在数学课堂中落实。

（责任编辑  袁 霜）