“总体教育方法”对结构力学教学和知识体系建构的启示

阙仁波

摘  要： 以位移法和矩阵位移法为例，演示了“总体教育方法”对结构力学教学和知识体系建构的启示。该方法强调以宏观方向感来引领微观进程，以及将分化的学科知识重新化合起来。具有方法论的指导意义。

关键词：总体教育方法;位移法;矩阵位移法;结构力学教学;知识体系建构;方法论

中图分类号：G642 文献标志码：A 文章编号：2096-000X（2019）16-0119-05

Abstract： By taking displacement method and matrix displacement method as examples， it was demonstrated in this paper how to draw an inspiration from "overall education method" for teaching of structural mechanics and construction of knowledge systems. In overall education method， the macro guidance for micro-process and the integration of differentiated subjects was highly emphasized. A meaningful guidance was provided from the viewpoint of methodology.

Keywords： overall education method; displacement method; matrix displacement method; teaching of structural mechanics; construction of knowledge systems; methodology

引言

林同炎和S.D.斯多台斯伯利在《结构概念和体系》[1]一书中曾指出，设计者在开始处理结构方面的问题时，必然希望在形成和处理总体方案时，着眼于相互有关的各主要分体系，而不是构件和细部构造。但是，与总体考虑的必然效果相反，建筑和工程的学生往往是通过学习基本构件及其有关的具体设计和施工要点来学习工程知识。该方法假设学生自己会反回去发现怎样把各部分结合成整体。但不幸的是，该假设很少会实现，因为学习的模式和设计思路的自然流程相反。构件教育方法侧重于具体结构构件设计，缺乏与总体系目标有关的基本知识，强调部分而不是总体。而总体教育方法则侧重于总体空间形式结构体系的设计，其优点是可提供一种总的思路去学习结构概念和体系，并将它们应用于建筑设计中，整体决定构件。故建议采用从总体到具体的推论式的教育方法，从介绍结构开始，在考虑方案时，将基本思路集中于主要的结构分体系，并分解出关键构件，以及为实现总体而需要的细部构造。

尽管该书发行距今已二十年，可将该段话放在现今土木工程教育的语境里，依然是切中时弊的同时亦附上了改革的良方，颇富启示。

受多方因素诸如“复合型”、“宽口径”、“厚基础”和“大土木”等提法的影响，课程门数增多，单门学时缩减，有限的学时所致的断章式的教学难以完成课程自身的知识架构，进而前后序课程之间的纵向进阶出现跳跃式中断，基本原理与应用演绎之间的横向联系松散，教与学均呈现出碎片化趋势。专业基础课的“浅基础”学习难以支撑起作为“上层建筑”的专业课学习，“工”缺乏“理”的有力支撑，学生不知所用原理源于哪里，不懂来龙去脉，难以反回去把前后联系起来，缺乏宏观的方向感。缺乏一定深度的基础，难称“厚基础”;缺乏逻辑、连续、有序和融会的体系建构，“复合型”、“宽口径”和“大土木”容易陷入混合而非化合的窘境，有限的体量在平面向的扩展只会导致深度向的浅薄，教与学均会由聚焦和结晶走向分散和稀释。

要解决上述矛盾，无论是教材的陈述模式，抑或课堂的讲解模式，均亟待改革和优化。而总体教育方法，作为一种合乎科学规律的方法，不失为一种好的选择。它以宏观引领和驾驭微观，以目标为导向，从总体分解出具体，具体到问题为已知，再反回去综合。在该过程中，催化了学科分化后的重新化合，加速内容的接受，在知识的贯通中实现体系的建构。逻辑清晰，可为学生的课外探索提供一种宏观的方向感，让他们自己去扩充知识体量，以缓解学时有限的困扰。

本文将以结构力学中的位移法和矩阵位移法为例，尝试说明一下采用总体教育方法的陈述模式。

一、对位移法教学的启示

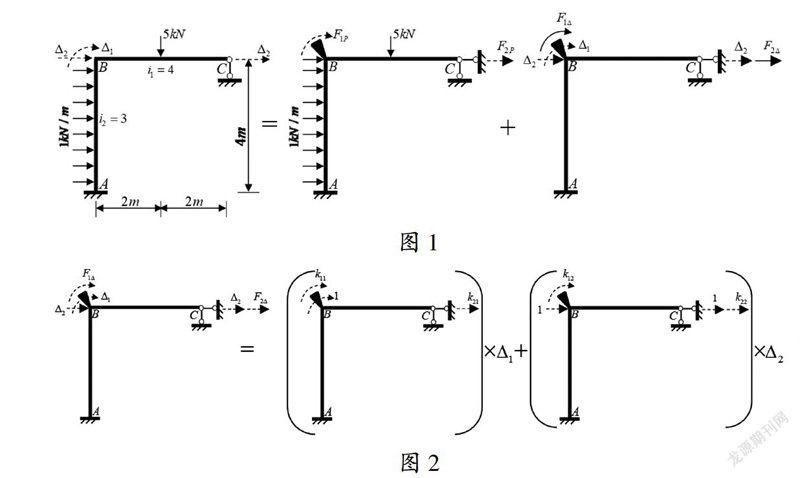
如图1左幅所示，若忽略轴向变形，结构在集中荷载和均布荷载作用下，结点B处发生角位移？驻1和水平线位移？驻2，结点C处亦发生与结点B处同样大小和方向的水平线位移？驻2。为求结点位移？驻1、？驻2和结构内力，分别在结点B处和结点C处附加可控约束来主动控制角位移和线位移：第一，如图1中幅所示，让结点不产生位移，仅受集中荷载和均布荷载作用，设在附加约束处分别产生约束力F1P和F2P;第二，如图1右幅所示，让结点B处产生角位移？驻1和线位移？驻2、结点C处产生线位移？驻2，设在附加约束处分别产生约束力F1？驻和F2？驻。在线弹性范围内，利用叠加原理，可得总的附加约束力为F1=F1P+F1？驻F2=F2P+F2？驻。附加约束属于虚构，实际结构并没有，故应满足F1=0F2=0，即附加约束起不到约束作用，与实际结构相同，由此可建立如图1所示的等效关系。正所谓：迷津欲渡，附加约束。

在线弹性范围内，利用叠加原理，以及约束力與结点位移成正比的关系，又可建立如图2所示的等效关系：F1？驻=k11？驻1+k12？驻2F2？驻=k21？驻1+k22？驻2。

综上所述，可得：k11？驻1+k12？驻2=-F1Pk21？驻1+k22？驻2=-F2P，此即位移法典型方程。

上述的附加约束可起两方面的作用：第一、作为可控约束，可用来主动控制结点位移，或使之不发生位移，如图1中幅所示，或发生指定大小的位移，如图2所示;第二、隔离构件，使它们成为各自变形、互不干扰的单个构件，从而将结构解构为一个两端固定的单跨超静定梁AB和一个一端固定、一端铰支的单跨超静定梁BC。

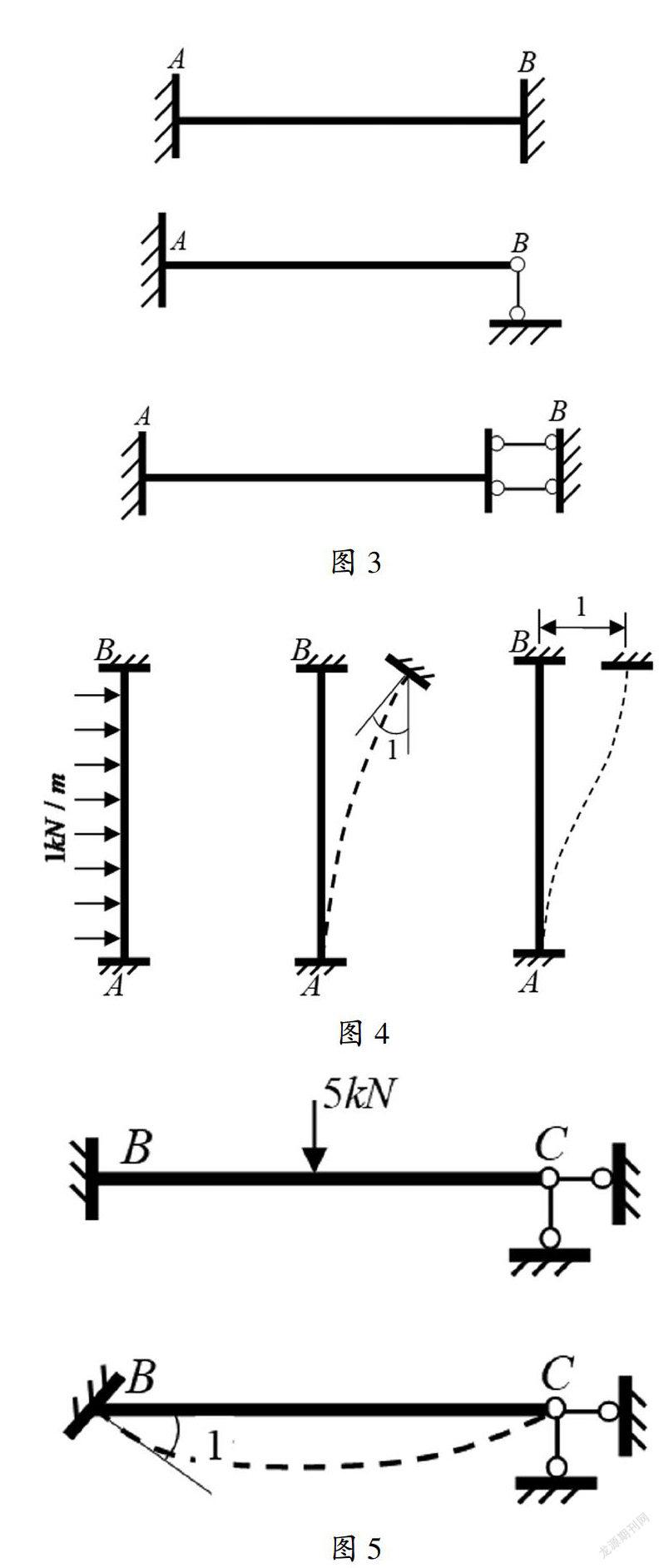
如图3所示的三种基本单跨超静定梁在荷载、杆端转角和侧移等作用下的杆端弯矩和剪力，均已通过力法推导出了相应的计算公式[2-3]。

故图1中幅所示的F1P和F2P、中幅和右幅所示的k11、k21、k12和k22可通过图4和图5分别求出各因素产生的各杆杆端弯矩和杆端剪力，再将其反向作用于相应的结点，通过考虑结点力矩平衡和杆件力矢投影平衡即可求出。从而通过位移法典型方程求出？驻1和？驻2，进而利用叠加原理通过M=M1？驻1+M2？驻2+MP即可求出MAB、MBA和MBC。其中MP、M1和M2分别为图1中幅、图2中幅括号内和图2右幅括号内的弯矩。该过程相当于一个从构件到结构的重构。

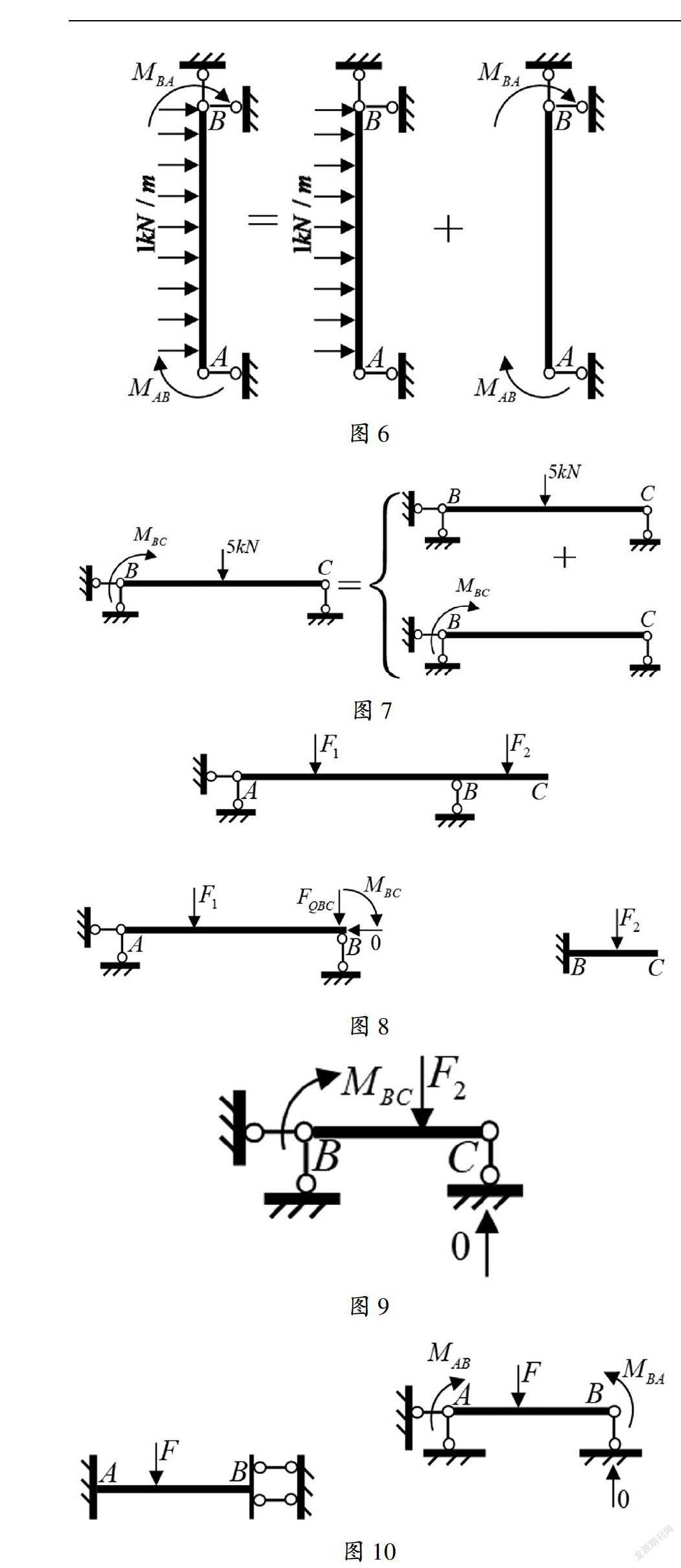
求出MAB、MBA和MBC后，由上一步分解所得的单跨超静定梁AB和BA可进一步解除杆端限制转动的约束并代以相应的约束力矩（大小和方向与相应的杆端弯矩相同），在忽略轴向变形的情况下，两端均有轴向约束时可解除其中一端的轴向约束，从而形成如图6左幅和图7左幅所示的简支梁，而简支梁的剪力、弯矩、剪力图和弯矩图的求解在构件（材料）力学中已学过。在线弹性范围内，可如图6和图7所示利用叠加原理求解。

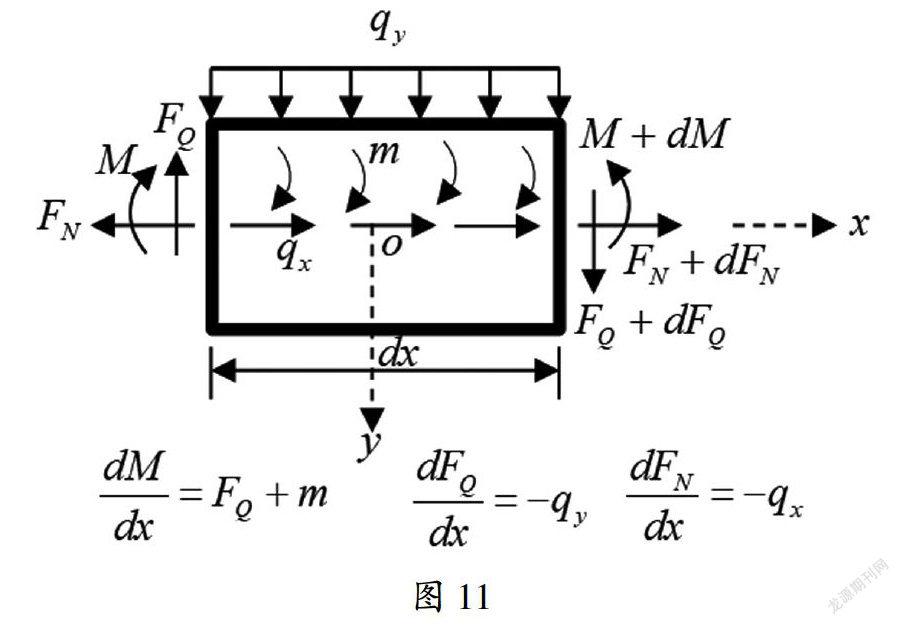
三种基本的单跨静定梁：简支梁、悬臂梁和伸臂梁（单向伸臂或双向伸臂），是构件力学研究的主要对象。实际上，如图8所示，上幅的伸臂梁，可分解为左下幅的简支梁和右下幅的悬臂梁，而右下幅的悬臂梁，又可等效为如图9所示的简支梁，只要解除B端限制转动的约束并代以相应的约束力矩MBC、而C点的支座反力为0即可。如图10左幅所示的单跨超静定梁，若忽略轴向变形，且已知MAB和MBA时，可等效为右幅所示的简支梁，其中B点的支座反力为0。故无论是图3所示的单跨超静定梁，抑或静定的悬臂梁或伸臂梁，最后均可化为简支梁来求其内力和作内力图。而对于直杆简支梁，可利用微分关系（如图11所示）来判断内力图形状，采用分段叠加法来作内力图。

求出构件内力后，即可进行构件的配筋设计、承载力复核以及结点和支座等细部构造设计。尽管实际中要考虑荷载组合，进行影响线计算，但宏观走向与上述思路基本一样。

纵观上述整个求解思路，结构计算简图来自实际工程的理论建模，计算分析从结构开始，通过虚构的附加约束，解构出杆端弯矩和剪力计算公式已知的单跨超静定梁，再通过重构，由结点力矩平衡或杆件力矢投影平衡，建立位移法典型方程，求解出位移基本未知量，进而杆端弯矩，再将单跨超静定梁解除杆端约束变为单跨静定梁，按构件力学求解其内力和作内力图，进行构件的配筋设计、承载力复核以及结点和支座等细部构造设计。从总体到具体，从结构到构件，从复杂到简单，从综合到单一，从未知到已知，虚构-解构-重构，可将结构力学、材料力学和结构设计原理等学科贯穿起来。

二、对矩阵位移法教学的启示

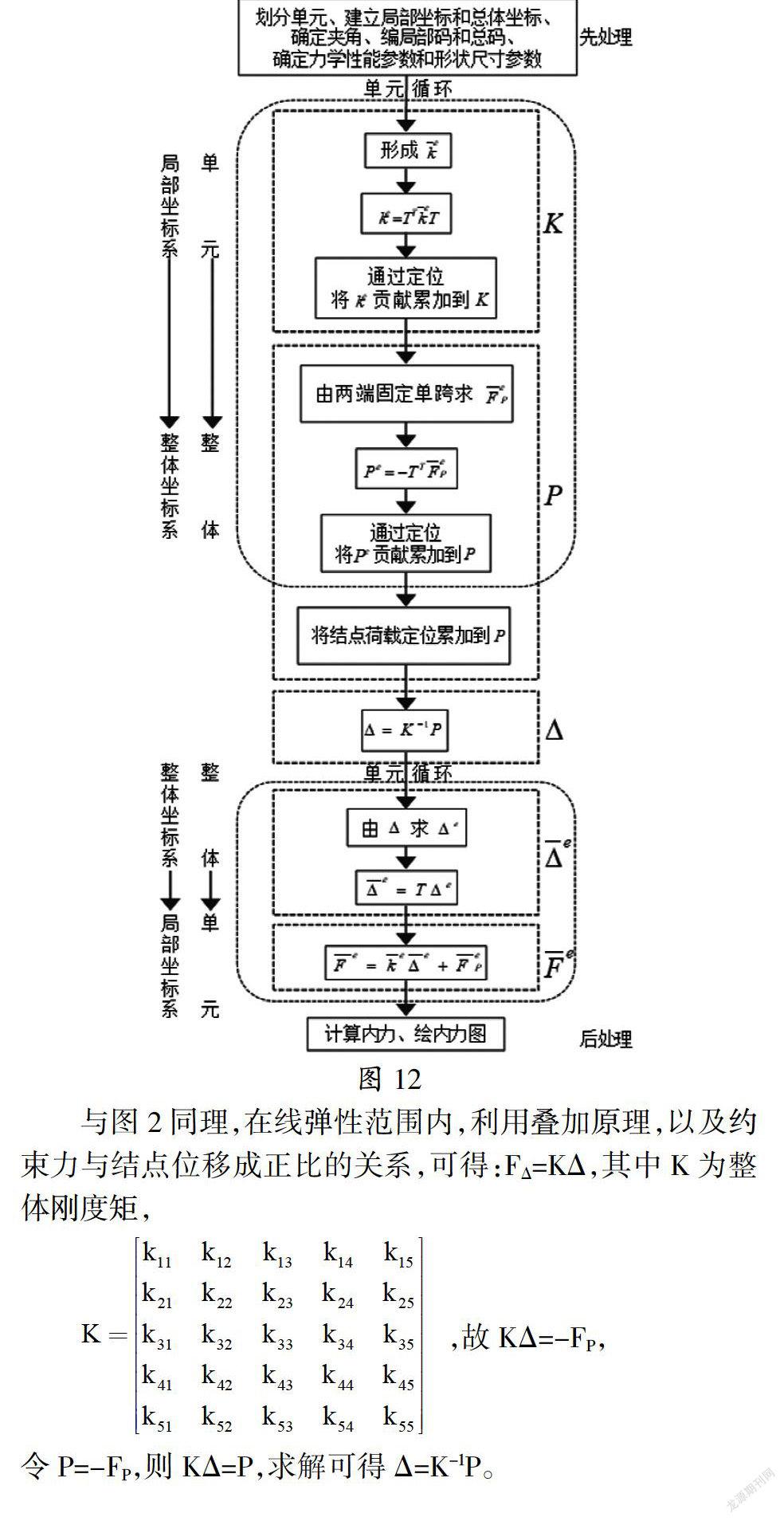
矩阵位移法的计算机程序实现步骤一般如图12所示（注：图中符号含义同文献[2]，在此不再赘述），故绝大部分教材亦都按从单元到整体、从局部坐标系到整体坐标系安排节序，但却往往缺乏先导性的整体思想的介绍，学生对节与节之间的起承转合、有关量的意义、量与量之间的联系等概念模糊，学习过程中对目标和走向缺乏预见性的宏观把握，直到各章节学完，才会有个总体的概念，问题的实质被淹没在大量数据组成的矩阵中，从而造成学习过程中的困难和畏难，难以理清内在的逻辑关系并通过计算机语言自主开发程序来进行计算。对此，总体教育方法大有用武之地。先导性地将问题总体提出，然后将目标不断分解，直至已知。最好以一个贯穿各个章节的问题为例，在讲解每一节的时候，都告诉学生该节具体是在解决哪个分目标，分目标完成后，再反过去集成。如此，宏观且直观。下面举例予以说明。

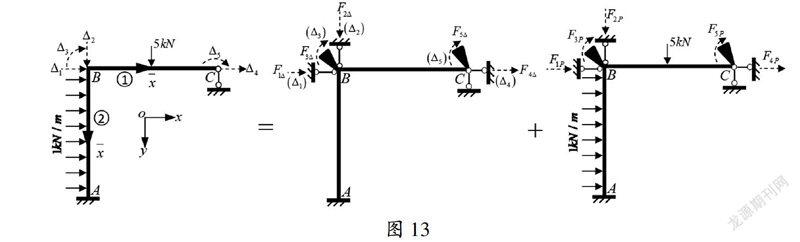
问题与图1左幅相同，但位移法不考虑轴向变形，通过附加可控约束将结构隔离分解为诸如图3所示的三种基本单跨超静定梁的形式;而矩阵位移法考虑轴向变形，且所有未知非零结点位移均为基本未知量，如图13左幅所示，通过附加可控约束将它们全部约束住而将结构隔离分解为均如图3上幅所示的单跨超静定结构。第一，如图13中幅所示，让结点B处和C处产生位移？驻=[？驻1 ？驻2 ？驻3 ？驻4 ？驻5]T，设在附加约束处产生约束力F？驻=[F1？驻 F2？驻 F3？驻 F4？驻 F5？驻]T;第二，如图13右幅所示，让结点不产生位移，仅受集中荷载和均布荷载作用，设在附加约束处产生约束力FP=[F1P F2P F3P F4P F5P]T;在线弹性范围内，利用叠加原理，则总的附加约束力为F=FP+F？驻。附加约束属于虚构，实际结构并没，故应满足F=0，即附加约束起不到约束作用，与实际结构相同，由此可建立如图13所示的等效关系。

与图2同理，在线弹性范围内，利用叠加原理，以及约束力与结点位移成正比的关系，可得：F？驻=K？驻，其中K为整体刚度矩，

上述即矩阵位移法的整体思想，其中，K、？驻和P等量的含义均已清晰地呈现。接下来即以此为分目标逐个求解。

附加约束力F可通过结点力矩平衡和结点力矢投影平衡由交于该结点处的各单元的杆端内力的反力和结点荷载求出，故先得求整体坐标系中的单元杆端内力（注意：是整体坐标系中而非局部坐标系中，因為只有统一到同一参考坐标系中，力矢才方便加减）。

而求杆端内力在局部坐标系中更方便，如图3上幅所示的单跨超静定结构在杆端位移和跨间荷载等因素作用下的杆端内力均有现成的公式可用，由此可写出局部坐标系中杆端内力与杆端位移和跨间荷载之间的方程。

将各单元局部坐标系中的杆端内力转换统一到整体坐标系中，再通过单元叠加的方式，即可求出FP和F？驻，进而求出？驻。不过由单元的F■■求整体的F？驻的过程，经由Fe=TTFe=TTke？驻e=TTkeT？驻e=ke？驻e转换成了求ke→ke→K的间接过程，而对于很多初学者，这一个转换过程，往往会把求Fe的实质给掩盖掉而变得不好理解，故教学中一定要加以强调。

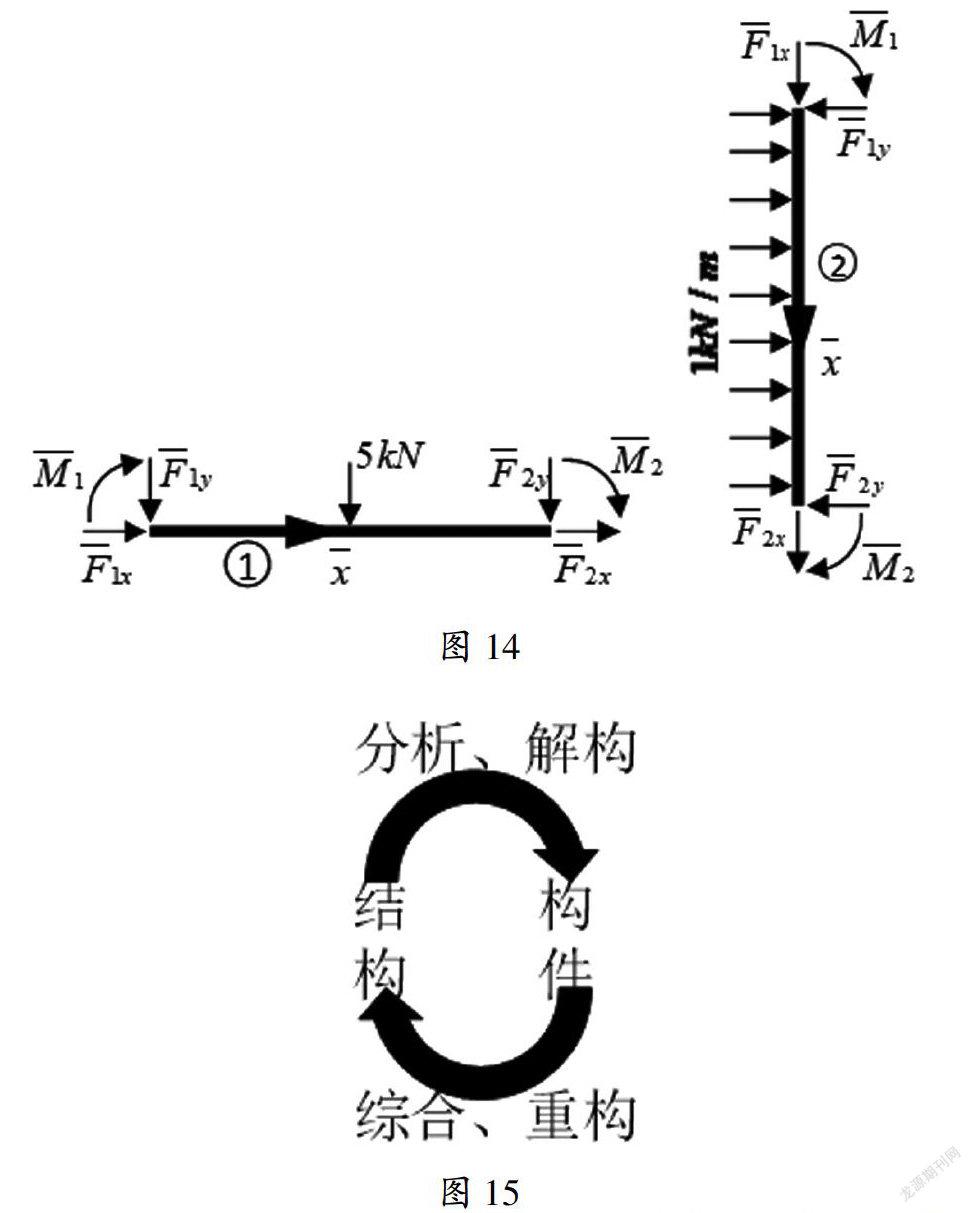
求构件的内力和绘内力图，在局部坐标系中比在整体坐标系中更合适，故作？驻→？驻e→？驻e→Fe的从整体到单元、从整体坐标系到局部坐标系的转换计算，可求得如图14所示的单元杆端内力，至此，又回到了构件力学，可利用微分关系（如图11所示，不过将改为）来判断内力图形状，采用分段叠加法来作内力图。

求出构件内力后，即可进行构件的配筋设计、承载力复核以及结点和支座等细部构造设计。尽管实际中要考慮荷载组合，进行影响线计算，但宏观走向与上述思路基本一样。

纵观上述整个求解思路，与循序渐进地“从单元到整体、从局部坐标系到整体坐标系”的阐述模式相比，上述模式通过先导性地引出总体思想，确定总目标，并不断分解为分目标，再逆序渐退地去逐步解决分目标并进行集成，问题的来龙去脉清晰，方向感强，各个过程的目的和意义明确。从总目标到目标分解、到解分目标、到集成，既实现了总体引领和驾驭具体，又“反回去发现怎样把各部分结合成整体”[1]，完成了如图15所示“反”和“正”的闭环。

尽管现在很多计算已交由现成的、基于矩阵位移法思想或更一般的有限元法思想开发的程序去完成，但透彻理解程序的内核思想，对于正确使用程序依然很有必要。在定量计算交由程序去完成的时候，更应加强定性分析和概念设计的能力。

三、对知识体系建构的启示

与由构件到结构的建构过程类似，大多数教育方法采取的都是“构件教育方法”，由于缺乏与总体目标的联系，在进阶过程中，学生对当前的定位、下一步的走向和曾经的来路往往不是很清晰，为弥补该缺陷，要充分发挥总体教育方法在该方面的长处。比如在结构力学教学过程中，不仅要能从静定结构的内力到静定结构的位移、到力法解超静定结构、到以已由力法求解给出公式的单跨超静定结构为基本单元进行求解的位移法和矩阵位移法的“顺”序进阶，亦要能按将复杂超静定结构解构为单跨超静定结构，再为单跨静定结构，再采用构件力学来求解的“逆”序降阶，经由虚构附加约束，将结构解构为构件，再分析构件，不断从复杂、综合和未知降阶到简单、单一和已知，再反过去重构，从而建立方程，求解基本未知量。拾阶而上，俯瞰回望，在融会贯通中达到进退自如。该种思维方法，不仅一以贯之地存在于位移法和矩阵位移法中，更存在于一般的有限元分析、建筑结构和桥梁结构等结构分析中，学习中要注意在类比中横向拓展。

为能实现如上所述的进退自如，不仅要弄清课程章节之间的进阶，亦要弄清课程与课程之间的进阶以及不同课程的明确分工与衔接点所在，比如为何位移法和矩阵位移法中强调更多的是求杆端内力，而非杆间内力，因为若已知杆端内力，杆间内力即可交由构件力学去求解。又如“结构的安全性是通过验算其强度、刚度和稳定性获得的。两阶段设计就是通过结构力学分析，确定结构在最不利荷载作用下的结构内力和结构刚度与稳定性，再由材料力学计算构件的强度与承载力，然后结合结构的连接、约束等的可靠性来判定结构的安全性。”[4]故结构力学里亦很少去探讨应力和强度问题，因为一旦构件内力求得，其应力和强度即可交由构件力学去求解，当然，因塑性引起应力重分布和结构几何组成变化的问题要将结构作为一个整体来考虑。

要重视专业基础课与专业课之间的“理论基础”与“上部建筑”的关系，如材料力学与钢筋混凝土结构、结构力学与建筑结构等，不仅应加强从理论到应用、从一般到特殊的演绎能力，亦应加强从应用到理论、从特殊到一般的归纳能力。在正向和逆向的往复中实现贯通。

在结构课如建筑结构和桥梁结构与作为基础的结构力学课之间，存在着一个如何从实际结构中抽象出计算简图的问题，国内的大部分结构力学教材往往只有计算简图，故学生在学习结构力学时缺乏对工程背景的感性认识，比较抽象，学习专业课时又存在如何从实际结构中抽象出计算简图的问题，两者之间鸿沟大。在这个问题上，可适当借鉴国外一些结构力学教材[5，6]的做法，配以相应的工程实际图，借以缩小实际结构与计算简图、结构课与结构力学课之间的鸿沟。

综上所述，总体教育方法，强调出乎其外以宏观，提供一种方向感;构件教育，则强调入乎其内以微观，追根溯源，看原理源于哪里;实际中，宜将两者相互结合。若光有构件教育，则易“微观分析过细，宏观蓝图匮乏”[7]抑或知识碎片化的，难以建构起宏观的知识体系。

四、结束语

1. 以位移法和矩阵位移法为例，演示了“总体教育方法”对结构力学教学和知识体系建构的启示。

2. 该方法强度以宏观方向感来引领和驾驭微观进程。从结构开始，通过虚构的附加约束，解构出构件，通过构件力学分析后，再重构还原，从而建立方程，求解基本未知量，再返回构件分析，完成一个闭环的迭代。

3. 将该方法的启示加以普遍化，可催化学科分化后的重新化合，加速知识的接受，在贯通中实现体系的建构。从“技”中提升出“道”，提供一种方法论的指导。

参考文献：

[1]林同炎，S.D.斯多台斯伯利.结构概念和体系（第二版）[M].高立人，等译.北京：中国建筑工业出版社，2012.

[2]龙驭球，等.结构力学I（第三版）[M].北京：高等教育出版社，2013.

[3]李廉锟.结构力学上册（第5版）[M].北京：高等教育出版社，2012.

[4]肖汝诚，等.桥梁结构体系[M].北京：人民交通出版社，2013.

[5]R.c.hibbeler. Structural Analysis[M]. 9th ed. Pearson， 2012.

[6]Kenneth M.Leet， et al. Fundamentals of Structural Analysis[M]. 4thed. McGraw-Hill Education， 2011.

[7][美]W.舒勒尔.建筑结构设计（上册）[M].罗福午，等译.北京：清华大学出版社，2006.