交换折叠超立方体的连通度

蔡学鹏，杨 伟，任佰通，冯苗苗

（新疆农业大学数理学院，新疆，乌鲁木齐 830052）

0 引言

随着计算机的飞速发展，信息化和数字化技术的不断进步，许多实际问题的数学模型使离散型结构上的数字化技术得到了更多人的关注，图的连通度理论[1-7]作为离散数学的一个重要的组成部分。多处理器系统由两个或两个以上的处理器构成，处理器交换各种信息是用消息协议通过互联网络传播的。在大规模集成(VLSI)技术和圆片规模集成技术(WSI)领域的最新进步已经能使含有非常多的处理器数量的处理器系统实现信息交流。因为增加的多处理器系统中处理器的数量、多处理器系统的可靠性和容错性的研究已经成为一个活跃的热门的研究领域，因此受到了国际数学界与工程界越来越广泛的重视。

本文仅考虑有限的、无向的、简单的并且连通的图[1,8-9]。

设G=G(V,E)是一个图。对于图G中两个子图H和K，记是点集诱导的子图。设NH(K)是在H中且与K中的点相邻的点的集合。特殊地，如果K={v}，可记作NH(v)。设是点v在图G中的度，设NG[v]=NG(v)∪{v}。如果不产生歧义，我们可省略下标即记为d(v),N(v),N[v]。δ(G)=表示图G的最小度。

设S⊆V(G)(或者S⊆E(G))，如果G-S是不连通的或者平凡的，则称S是图G的一个点割（或者边割）。连通度（或者边连通度）是衡量网络可靠性的一个重要参数。图G的连通度κ(G)（或者边连通度λ(G)）是图G中最小点割（或者边割）的基数。我们知道κ(G)≤λ(G)≤δ(G)，并且κ(G)（或者λ(G)）越大图G就越可靠。

互联网络的拓扑结构经常被表示成一个连通的图，其中图的点和边分别表示互联网络的处理器和互联网络的连接线[9]。在平行计算系统中，n维超立方体Q[10]，n维折叠超立方体FQnn[11]和交叉超立方体EH(s,t)[12]是三个重要的互联网络。基于这三个网络，李[13]等人在2005年提出了一个新的网络交换折叠超立方体EFH(s,t)。EFH(s,t)是在EH(s,t)的基础上增加了一些额外的边获得的，并且这些边称为补边。交换折叠超立方体有许多重要的特性，比如它有短的直径和低消费因子。最近，K.Bhavani[14]等人研究了交换折叠超立方体中的短路径问题。有关交换折叠超立方体的详细内容参见文献[13-14]。

我们都知道κ(Qn)=λ(Qn)=n。马[2]证明了κ(EH(s,t))=λ(EH(s,t))=s+1，其中1≤s≤t。本文将证明κ(EFH(s,t))=λ(EFH(s,t))=s+2，1≤s≤t。

1 预备知识

一个二进制n元字符串x=xn-1xn-2…x0的第i个字符xi记为x[i]，0≤i≤n-1。

定义1.1[2]设交换超立方体EH(s,t)=G(V,E)，s,t是正整数。交换超立方体EH(s,t)的点集

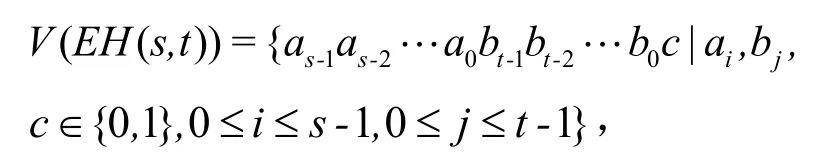
边集E(EH(s,t))={(u,v)|(u,v)∈V(EH(s,t)×V(EH(s,t)}是由三种类型的边E1,E2,E3构成。

其中

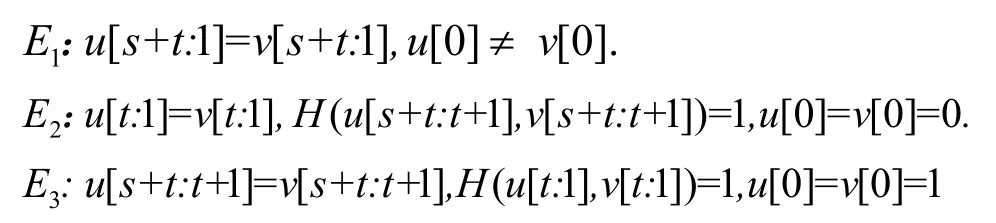
通过定义，立即可得EH(s,t)的点数EH(s,t)的边数(s+t+2)2s+t+1。设(u,v)∈E(EH(s,t))，对 某 个i=1,2,3,⋅⋅⋅,s+t，u[i]=v[i]且u[j]≠v[j]，j≠i，此时称边(u,v)是i-边。如果EH(s,t)中两个点u和v通过i-边相邻，则称u和v沿维数i相邻。我们也称u是v的i-邻点，记作v=ni(u)。因为EH(s,t)是Qn的一个子图，所以EH(s,t)是一个二部图。

定义1.2[13]交换折叠超立方体，记为EFH(s,t)，它是由交换超立方体EH(s,t)中的任意两个互补的点增加一条边后得到的。这些新增加的边称为EFH(s,t)的补边，它们构成的集合记为E4。

EH(1,2)和EFH(1,2)的图见图1。

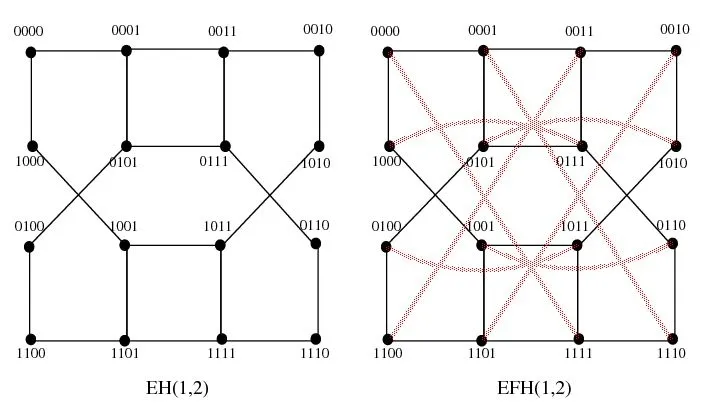
图1 EH(1,2)和EFH(1,2)Fig.1 EH(1,2) and EFH(1,2)

通过定义 1.2，EFH(s,t)中点数2s+t+1，EFH(s,t)包含四种不同类型的边。E1型边：条，E2型边：条，E3型边条，E4型边条。EFH(s,t)中边的总数如果u[0]=0，则d(u)=s+2，否则d(u)=t+2。

引 理 1.1[2]κ(EH(s,t))=λ(EH(s,t))=s+1，1≤s≤t。

引理1.2[12]EH(s,t)同构与EH(t,s)。

引理1.3[13]EFH(s,t)同构与EFH(t,s)。

通过引理1.2和引理1.3，我们可以在下面讨论中设s≤t，则δ(EH(s,t))=s+1且δ(EFH(s,t))=s+2。

引理 1.4[12]EH(s,t)可分解成两个EH(s-1,t)或两个EH(s,t-1)。

引理1.5[12]EH(s,t)是2-连通的。

引理1.6[13]EFH(s,t)是2-连通的。

2 交换折叠超立方体的连通度

引理2.1κ(EFH(1,t))≥3，t≥1。

证明：设F是EFH(s,t)中的任意一个点集且我们将证明EFH(s,t)-F是连通的。

t=1时，结论明显成立。

现设t2，EFH(s,t)可被分解成为子图L1和子图R1，其中

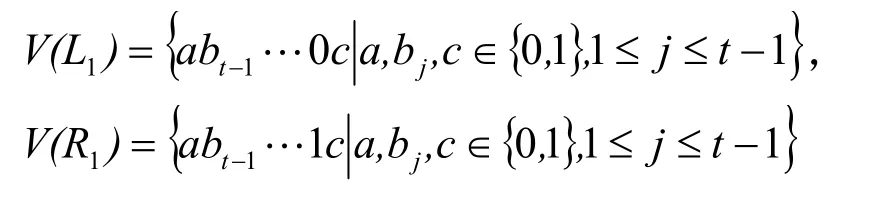
L1和R1分别是由点集V(L1)和V(R1)诱导的子图。明显地，L1和R1都同构于EH(1,t-1)，并且连接L1和R1的边都是由E3和E4构成。

因为R1同构于EH(1,t-1)，由引理 1.1知，R1-FR1是连通的。下面证明L1-FL1中的任何一个点通过一条路与R1-FR1中的一个点连通。考虑下面两种情形：

情形 1.设u=abt-1…b101，则n2(u)=abt-1…b111是u在R1中的一个邻点。如果n2(u)∉FR1，则结论成立。因此假设n2(u)∈FR1，那么是u通过E4中的一条边相连的邻点。通过定义，则设是连接u到R1中点的一条路。

情形 2.设u=abt-1...b100，注意到如果结论成立。因此假设设NL1(u)=如果设是一条连接u到的路，如果设是一条连接u到的路，因此证明完成。

定理2.1κ(EFH(s,t))=s+2,1≤s≤t。

证明：EFH(s,t)可分解成两个子图L和R，其中L和R分别是由点集V(L)和V(R)诱导的子图。明显地，L和R都同构于,t)EH(s-1，并且L和R之间的边是由E2和E4构成。

如果s=1，则δ(EFH(s,t))=s+2=3，由引理2.1，可以得到κ(EFH(s,t))=s+2=3。

设s1，由引理1.1，可知κ(L)=κ(R)=s。设S是EFH(s,t)的一个最小的点割，令

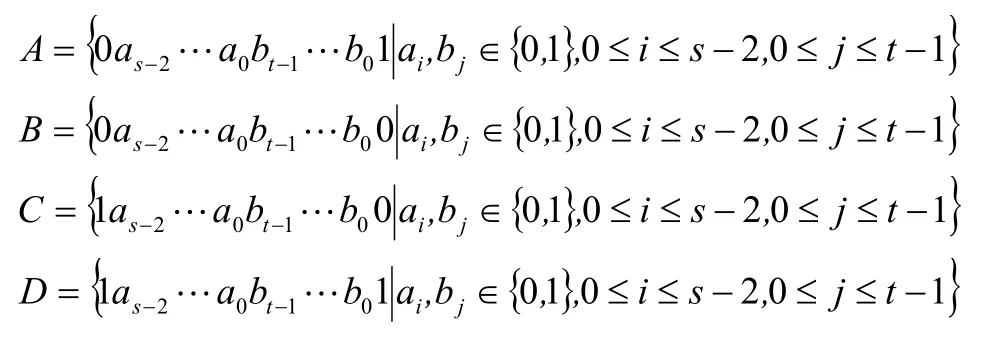
则有A∪B=V(L)且C∪D=V(R)。A与B（C与D）之间的边位于E1中且构成由点集A∪B(C∪D)诱导的子图的一个完美匹配。B与C之间的边位于E2中且构成了由点集B∪C诱导的子图的一个完美匹配。A与C（B与D）之间的边位于E4中且构成了由点集A∪C(C∪D)诱导的子图的一个完美匹配。

下面分两种情形计算。

情形1.L-S和R-S都连通。

我们容易知E4中每条边的至少一个端点都属于S。即有此时EFH(s,t)-S是连通的，这与S是点割矛盾。

情形2.L-S或者R-S不连通。

不失一般性，假设L-S是不连通的。通过引理1.1，S在L中至少有s个点。方便起见设SL SL=∩且SR=S∩R。

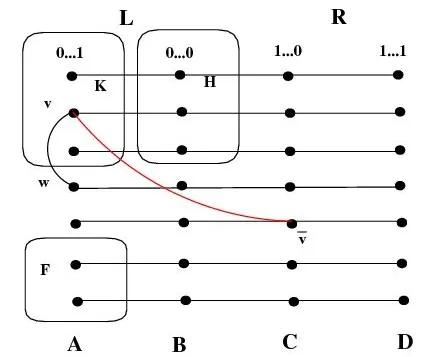
图2 定理2.1证明中情形2的解释Fig.2 Illustration of the proof of Case 2 of Theorem 2.1

由于R同构于EH(s-1,t)并且EH(s-1,t)是2 -连通的，因此可知R-SR是连通的。因为B-H中的每一个点在R都有两个邻点，所以由点集V(R)∪(B-H)诱导的子图Q是连通的。因此移除S必须使得K中的某个点v与 Q不连通。通过EFH(s,t)的定义，可知且如果那么点v与Q通过E4中的一条边相连，矛盾产生。现在假设则否则v在A-K-F中至少有一个邻点w，并且v通过点w和E1中的边与Q连通，因此与

由于δ(EFH(s,t))=s+2，则κ(EFH(s,t))≤s+2。又因为S是一个最小的点割且可得κ(EFH(s,t))≥s+2，即κ(EFH(s,t))=s+2。

由κ(EFH(s,t))≤λ(EFH(s,t))≤δ(EFH(s,t))，有以下的定理2.2。

定理2.2λ(EFH(s,t))=s+2，1≤s≤t。

3 小结

本文主要研究了衡量交换折叠超立方体网络EFH(s,t)的可靠性的两个重要参数连通度和边连通度，最终决定了κ(EFH(s,t))=λ(EFH(s,t))=s+2,s≤t。