培养逻辑推理 提升数学运算——“数列求和”教学案例

张强

（内蒙古巴彦淖尔市乌拉特中旗第一中学，内蒙古巴彦淖尔 015300）

1 背景

数列作为高中数学的重要内容，是历届高考的必考内容。数列教学的核心素养——逻辑推理和数学运算。借助我国先人之数学经典展开教学，让学生感受我国文明之璀璨，把握三维目标，体现数学价值，呈现数学魅力。数列求和作为数列教学的重要模块，是以两个基本数列——等差数列和等比数列为基础，进一步提升逻辑推理和运算能力，学会建立一般数学模型，强化实际问题的考察。在解决具体问题时，要熟练运用分类讨论、转化归纳、类比推理等数学思想，将表象很难求和的问题转化为我们熟悉的求和形式。本节课从公式法求和、分组求和、并项求和、裂项求和、错位求和五个角度，阐述数列求和的方法，遵循学生循序渐进的认知规律，让学生在感知知识的同时，感受数学的乐趣。

2 教学设计

2.1 提出问题 画龙点睛

教师：数列的基本就在于等差数列和等比数列，对于这两种数列，我们怎样求和，看下面的问题。

问题1：

⑴2+4+6+…+2n=

⑵1+2+2+2+…+2=

学生1：这两个数列求和，直接用等差数列和等比数列的前n项和公式求解。答案是n(n+1),2-1

教师：有不同意见吗？

学生2：第⑵题应该有n+1项，答案是 2-1

方法点睛（教师）：同学们，利用公式法求和，一定要搞清首项、公差（公比）以及数列的项数。

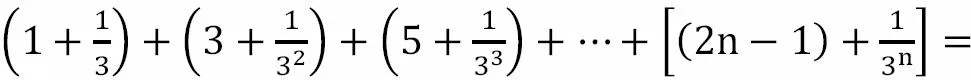
教师：请同学们认真观察，我们能否对该数列求和。

方法点睛（教师）：通过分组，得到等差或等比数列，分别求和再相加即可。这种方法叫做分组求和法。

问题3：S=1-2+3-4+…+(-1)·n，当n为奇数时，S= ，当n为偶数时，S=

学生4：类比问题2，利用分组求和法。（实物投影展示）

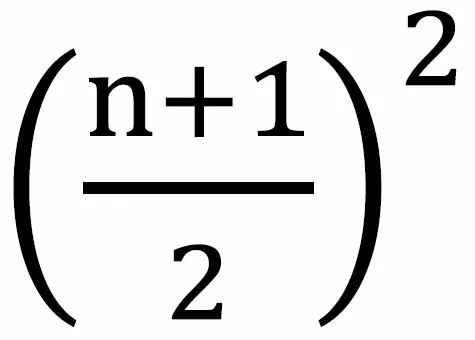
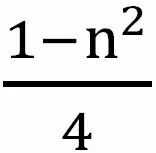
教师：同学们，还有其他方法吗？

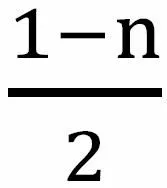
方法点睛（教师）：学生5的方法，把数列的若干项合并，得到一个常数列（也可能得到等差或等比数列），再进行求和，这种方法叫做并项求和法。显然，问题3使用并项求和法更为简单。

问题4：

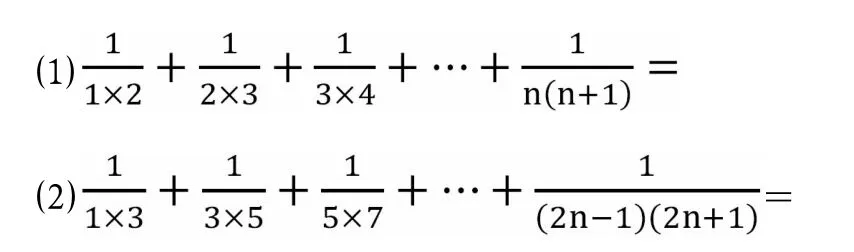
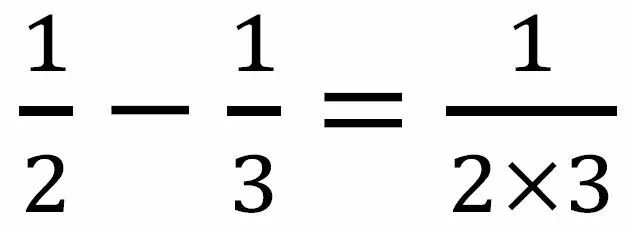
方法点睛（教师）：这两个数列求和，都是把数列中每一项拆成两项之差，并消掉若干项，实现求和。第二个数列求和，需配一个常数，才能拆项。同学们要体会其中的数学奥秘。这种数列求和的方法叫做裂项相消法。

常见的拆项公式：

问题5：1·3+2·3+3·3+…+n·3=

教师：同学们，仔细观察，我们能有什么方法求和？学生8：令S=1·3+2·3+3·3+·+n·3……①

两边同乘3，得：3S=1·3+2·3+3·3+…+n·3……②

①—②得：-2S=1·3+1·3+1·3+…+1·3n·3

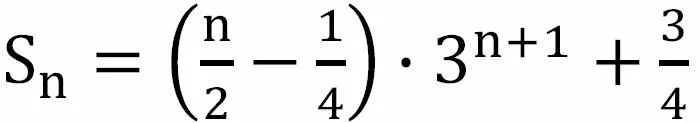
方法点睛（教师）：这个问题，我们利用等式的性质和方程的思想，通过错位相减转化为等比数列求和的问题，最终实现对该数列的求和。这种数列求和的方法叫做错位相减法。

2.2 归纳总结 有效提高

教师：本节课我们学习了哪些数列求和的方法，请同学们总结一下。

学生9：我们学习了公式法求和、分组求和法、并项求和法、裂项相消法、错位相减法。

教师：很好，数列求和是本章的难点，不同的数列求和方法不同，重在研究数列的形式和通项公式。通过分析、归纳、类比，得到数列的一些规律，联想相应的求和方法，既是根本，也是关键。数列求和的实质就是求数列{S}的通项公式，它几乎涵盖了数列中所有的思想策略，方法和技巧。所以请同学们谨记：方法不万能，尝试是关键，猜想要大胆，百练定成功。

3 教学反思

（1）数列求和对学生的知识和思维有很高的要求，通过自主学习、合作探究，激发学生的兴趣，调动学生的主观能动性。遵循学生的认知规律，与学生同步而行。不断挖掘学生的潜能，启发学生的思考方向和思维角度，把握学生的学习情绪，获得学习的乐趣。在解决问题的过程中，学生找到了方法与技巧，必然带来思想上的波澜，情感上的感染，价值上的认可，从而不断提升学生的核心素养。

（2）教师在教学过程中，充分的参与，恰当的点拨，肯定的关注，合理的引导。把握教学环节的突发事件，应对自如，注重细节，使学生获得知识的同时，产生对数学学习的浓厚乐趣。并不是所有学生都能掌握本节课的内容，但肯定的赏识，适当的鞭笞，定能让学生充满自信，这也是核心素养的体现。

4 结语

高中数学教学以发展学生数学学科核心素养为导向，创设合理的教学情境，运用各种教学方法，启发思维，激发兴趣，使学生养成良好的学习习惯。不断引导学生感悟数学的科学价值、应用价值、文化价值和审美价值。