一种高性能R-LWE格加密算法的电路结构及其FPGA实现

芮康康 王成华 范赛龙 刘伟强

（南京航空航天大学电子信息工程学院，南京，211106）

引 言

在信息安全问题越来越突出的背景下，需要更高安全性的加密算法来保障个人信息和隐私。解决信息安全问题，最常用的手段是对信息进行加密。目前，后量子密码（Post-quantum cryptography）[1]已成为国内外众多学者的重点研究对象。此类加密技术基于特定数学领域的困难问题，不依赖于任何量子理论现象，但其计算安全性可以抵御当前已知任何形式的量子计算攻击。更为重要的是，它们与当前网络系统具有较高的兼容性。美国国家标准局（NIST）[2]、美国国家安全局（NSA）[3]以及欧洲电信标准协会(ETSI）[4]正在制定后量子密码标准，预计2018年左右NIST将发布首批后量子密码标准。

基于格难题的密码算法是目前公钥加密技术中一个新的研究热点，此类密码算法具有加密效率高、硬件实现简单及抗量子攻击等优点，是后量子时代极具潜力的密码方案。而在由格难题构造的公钥密码方案中，基于环错误学习(Ring-learning with error,R-LWE)的加密方案在性能上有着较显著的优势[5]，它不仅具有基于格难题构造的公钥加密方案的各种优点，而且还支持理论安全性的证明[6]。文献[7]设计了一种R-LWE加密方案中的多项式乘法器，它是一种基于快速傅里叶变换（Fast Fourier transformation，FFT）的高效乘法器，硬件资源消耗较少。在传统设计中，人们通常通过降低系统时钟频率、减少冗余信号翻转等方法来降低系统功耗[8]，但是工作效率和系统性能也会随之下降。

本文提出了一种基于R-LWE格加密中多项式乘法的硬件结构。为了加快多项式乘法的运算速度，本文使用数论变换(Number theoretic transforms,NTT)方法，通过两个并行的蝶形运算PE（Processing element）处理单元，加速NTT的实现。在保证资源消耗较低的前提下，本文的实现较大地提升了运算速度。

1 格加密算法原理

1.1 格加密理论

根据向量空间的概念，格的定义[9]如下：

定义v1，v2，…，vn∈ Rm设为一组线性无关的向量。由v1，v2，…,vn生成的格L指的是向量v1，v2，…，vn线性组合构成的向量集合，且其所使用的系数均在整数域Z中，即L(v1，v2，…，vk)={a1v1+a2v2+…+anvn|a1，a2，…，an∈Z}。

任意一组可以生成格的线性无关的向量都称为格的基，格的基中的向量个数称为格的维度。任意两组这样的向量中，向量的个数相同。格类似于向量空间，但格是由基中的向量使用整数系数进行线性组合而构成的，而向量空间使用的则是任意系数。直观上，经常将格看成是按规律排列的属于Rm的一系列点，每个点都是一个向量的末端。

目前最常用的两个基于格的困难问题是短整数问题(Shortest integer problem，SIS)和错误学习问题(Learning with error，LWE)，这两个问题都可以看作等同于格问题的最短向量问题 (Shortest vector problem，SVP)上。但是基于SIS和LWE问题的加密方案都无法在实际中应用，这是因为随着安全参数的增大，这些方案需要非常大的密钥长度，资源消耗会迅速增加，效率迅速降低。因此，为了解决这个问题，Lyubashevsky等在LWE问题的基础上，提出了基于特定环上的LWE问题[10]。R-LWE算法是在环Zq[x]/(f)上进行的操作，其中f是n的不可约多项式，在大部分情况下，f=xn+1，则环为R=Zq[x]/(xn+1)，其中n是2的幂，q是一质数，如q=1 mod 2n。

R-LWE问题与LWE问题在形式上十分相似，并且具有标准LWE问题的很多特性，两者的搜索问题和判定问题几乎可以等价。Lyubashevsky等证明了：如果用多项式量子时间算法求解理想格上的SVP问题是困难的，那么对于任何的量子时间算法来说，求解R-LWE问题也将是困难的[10]。

综上，R-LWE加密方案的不足之处在于加解密过程中使用到了多项式乘法，使得R-LWE方案的电路设计较之于LWE方案更为复杂（LWE公钥长度大），电路开销也变得更大。但是与RSA,ECC等涉及到指数运算的加密方案相比，R-LWE方案仍旧比较易于设计且节省资源。经典和后量子公钥密码对比如表1所示。

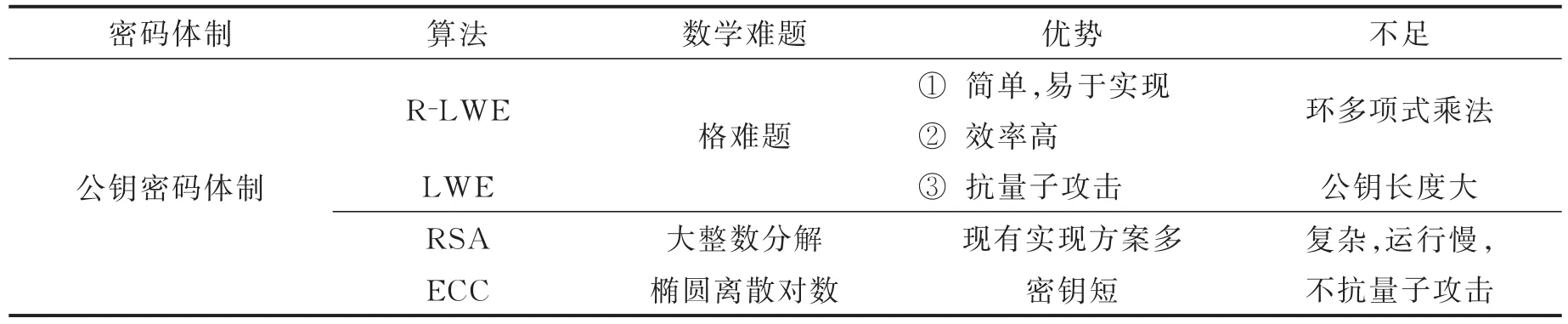
表1 经典和后量子公钥密码对比Tab.1 Comparison between classical and post quantum public key cryptography

1.2 格加密算法流程

格加密算法方案主要包括密钥生成、加密和解密3个部分[11]，具体实现如算法1所示。

算法1基于R-LWE的公钥密码算法

密钥：选择r1,r2服从高斯分布Dσ，令p=r1-t·r2∈ R。则公钥为p，私钥为r2。r1为高斯噪声，生成密钥后不再需要。t∈R在加密过程中保持不变，满足均匀分布。

加密：输入信息为m∈{0,1}n，选择e1,e2,e3服从高斯分布Dσ。令=f(m)∈R。则密文为[c1=

解密：解密的结果为m′=c1·r2+c2∈ {0,1}n。其中，Dσ是整数域上的离散高斯分布，期望是0，标准差是σ；R是多项式环Zq[x]/(xn+1)，q为素数且q=1 mod 2n，n为多项式的最高次数，f(m)实现模域变换，将输入信息从[0,1]信息范围转换到[0,q-1]的范围。

2 环多项式乘法

对于R-LWE密码算法，其中最为重要且耗时的是环多项式乘法。环多项式乘法有两种实现方式，分别为SchoolBook乘法和NTT数论变换乘法方法。

2.1 SchoolBook乘法

SchoolBook多项式算法公式为

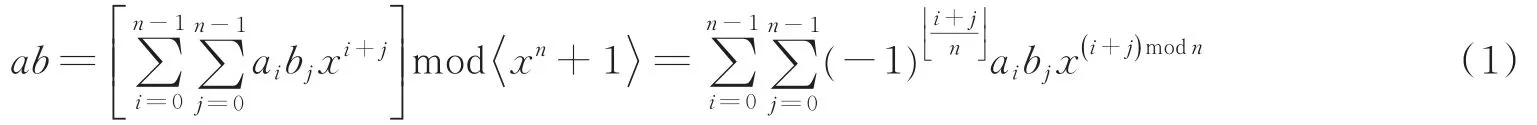
经典的SchoolBook多项式乘法复杂度为O(n2)，需要n2个乘法和(n-1)2个加减法。由于n是2的幂，模n操作可以实现为一个右移的寄存器，对于时，它等于1，否则i+j≤ 2n-2时等于-1。对于经典的SchoolBook算法实现，资源消耗较少，但是运算耗时较长。

2.2 NTT数论变换乘法

NTT是在FFT的数论基础上实现的。由于FFT是在复数域上的变换，而且还是浮点运算，存在精度和效率的问题。而在很多应用中，需要对整数商环内的序列进行变换，在这种情况下FFT性能无法满足要求，而NTT却能很好地解决这一问题。NTT变换形式与FFT一样，只是将FFT中的旋转因子由复数变成了整数，避免了浮点运算，使得运算效率也大为提高[12]。

数论变换是以正整数q为模的整数环Zq上定义的线性正交变换。设x(n)∈Zq，n=0,1,2,…,N-1，k=0,1,2,…,N-1，则称

为NTT，式(2)和式（3）分别为NTT正变换和NTT反变换。其中w为模q的N阶本原单位根，满足

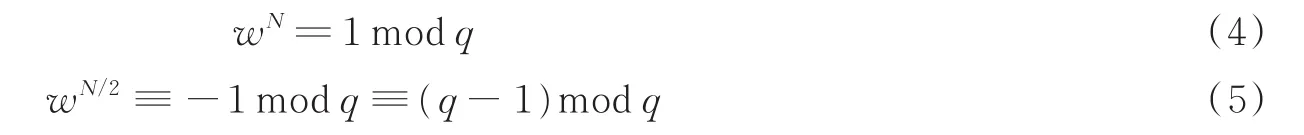
为整数且满足

用时间抽取算法将原序列x(n)按照序号的奇偶性拆分成两个序列x1(n)和x2(n)，则对应的NTT变换变为

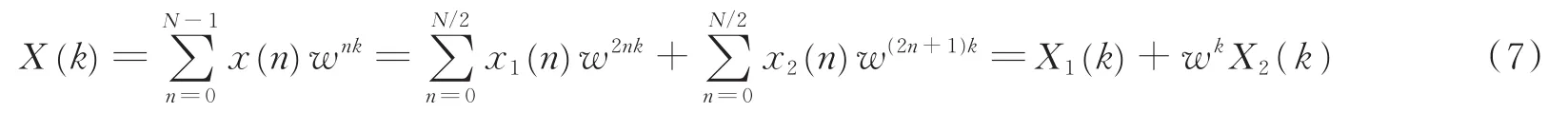
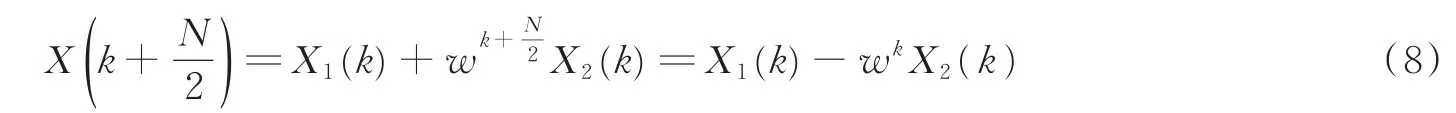
通过将原N点的NTT变换进行拆分，得到的新序列X1(k)，X2(k)变为N/2点的NTT变换。继续将X1(k)，X2(k)进行拆分，得到N/4点的NTT变换。依此类推，直到得到2点的NTT变换，即

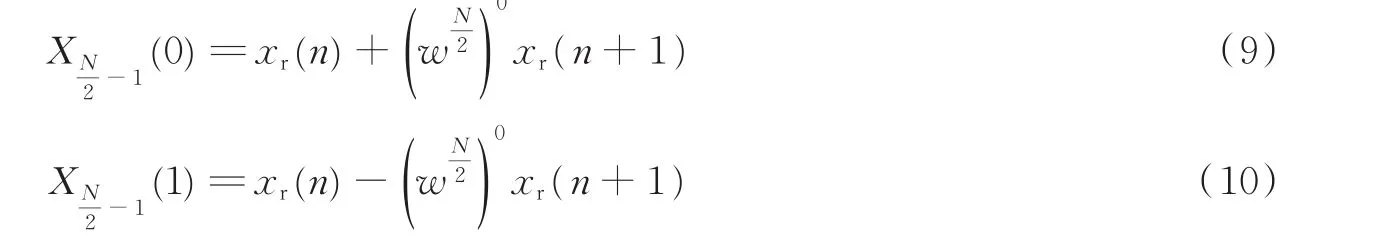
将k的取值范围变为原来的一半，则式中xr(n)为x(n)序列序号位倒置之后的排列。

以上进行的运算称之为蝶形运算，求一个N点的NTT，共需要执行log2N轮的蝶形运算。为便于理解，NTT变换的过程可以用蝶形图来描述，本文以8点的蝶形图为例，具体如图1所示。

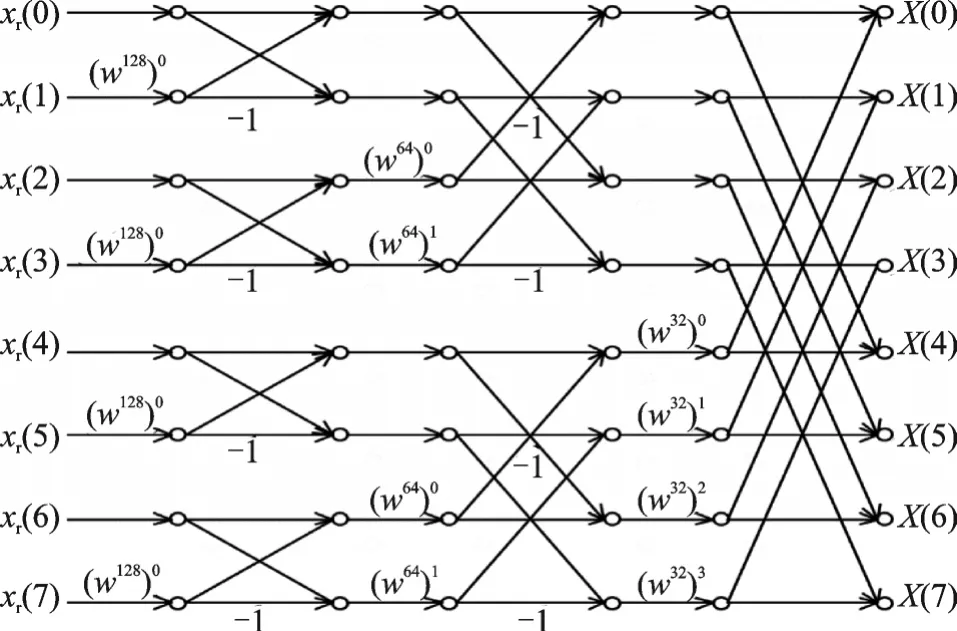
图1 8点NTT蝶形运算结构Fig.1 Butterfly structure of eight-point NTT

对于NTT多项式乘法而言，需要先将多项式进行数论变换，然后对应元素相乘，最后再进行逆数论变换，即可得到多项式乘法结果。NTT多项式乘法算法如算法2所示。

算法2NTT多项式乘法算法

输入：a,b∈Zq

输出：c∈Zq

A=NTT(a),B=NTT(b)

fori=0：n-1

C[i]=A[i]·B[i]

end

c=NTT-1(C)

returnc

3 NTT环多项式高效乘法器硬件设计

本文所使用的参数取自于文献[7]：多项式环系数的最高次数n=128，模质数q=216+1=65 537。本文设计的多项式乘法器电路结构如图2所示。

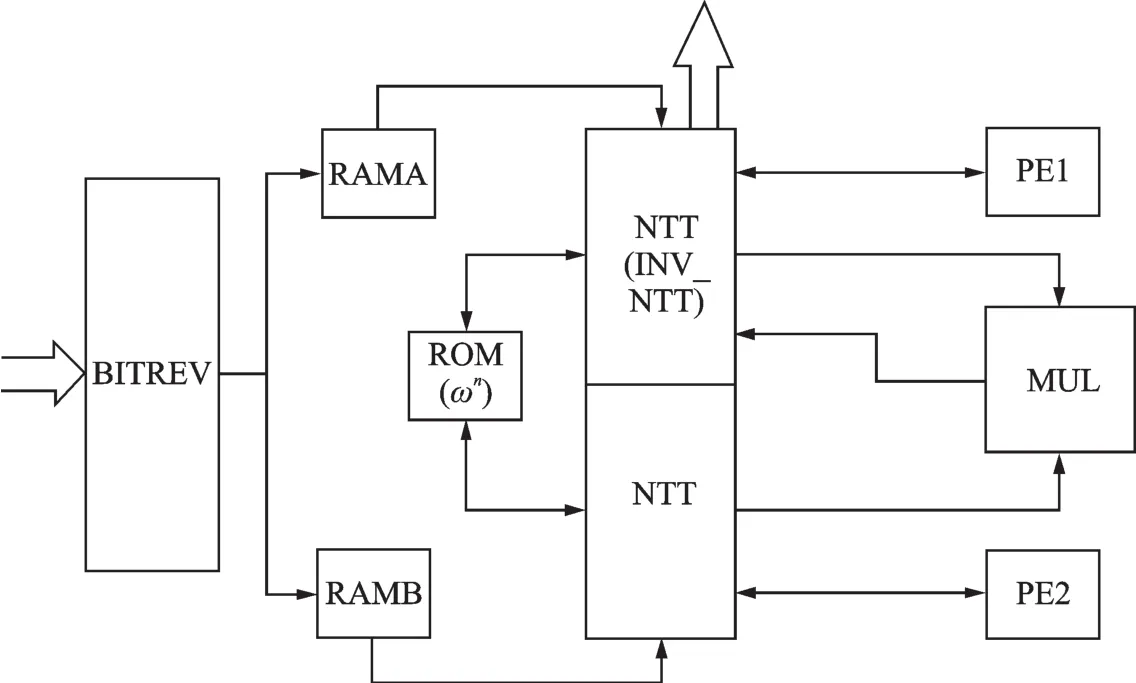
图2 本文实现的多项式乘法器结构Fig.2 Structure of the polynomial multiplier implemented in this work

本文设计的R-LWE方案中的多项式乘法器结构由PE,NTT和MUL等部件组成。PE单元是NTT的一部分，本文在图中把PE独立出来，是为了单独说明PE单元，本文的代码实现中PE与NTT也放在了两个不同模块。首先是BITREV模块，该功能是进行NTT变换之前的预处理，将原序列进行位置置换排序，得到蝶形运算的顺序，并控制从存储器RAM中读写数据。接着是RAMA和RAMB存储模块，这两个模块用来存储多项式系数a和b，RAM的大小是128×17 bit。系数ai和bi按序加载到乘法器中，并存进RAM。NTT模块也具有逆NTT的功能，区别是输入的旋转因子不同，它与PE处理单元相连，共同完成NTT数论变换的功能。此处的NTT模块主要是控制从存储器中读取相应的数据，然后将相应的数据按序送入蝶形运算单元，接着将蝶形运算单元输出的结果返回到NTT中，再调用下一次蝶形运算，每次变换均需要2×7轮操作，每一轮运算的结果作为下一轮运算的初始值。PE处理单元模块就是蝶形运算单元，包括乘加和取余操作，每个时钟周期计算NTT的一个节点，将处理完成的结果返回NTT模块。进行NTT数论变换后，a,b各个系数将在MUL乘法单元中对应相乘，然后将得到的结果送到逆NTT模块中，进行逆数论变换得到最终的结果。

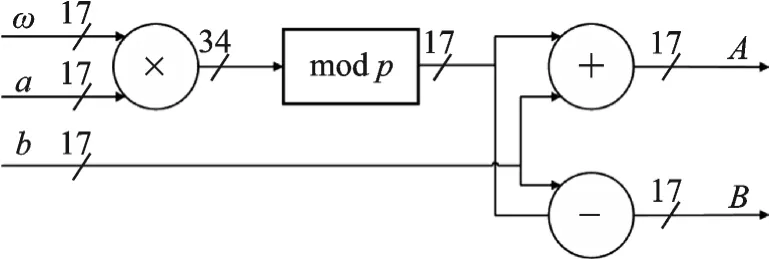
图3 PE处理单元结构Fig.3 Structure of PE processing element

PE处理单元的结构电路如图3所示。根据蝶形运算规则，将系数a和旋转因子相乘然后取余，最后是加减b运算。对于取余操作，余数是p=216+1=65 537。因此可得

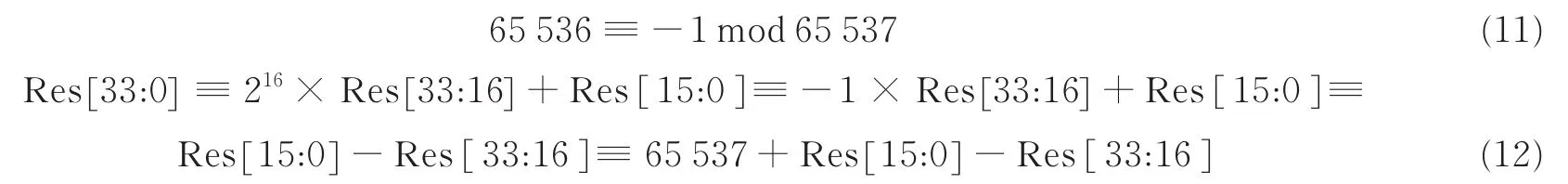
因此可将取余操作转化为简单的加减操作，比起直接调用Xilinx的取余IP核大大节省了资源消耗。

本文多项式乘法器的设计包含了两个PE处理单元和两个NTT数论变换模块，这样在进行NTT变换时，a和b两个多项式系数可以同时进行变换运算。蝶形运算需要的旋转因子是相同的，因此两个模块旋转因子可以直接获取得到，不需要重复调用，性能得到了大幅提升。在执行逆向NTT时，由于只有一个多项式需要运算，故只需要用到一个逆NTT模块，PE模块为NTT和逆NTT模块重复调用，节省了资源，也不消耗额外的时钟。本文的设计采用并行电路结构，是一种以提升速度为目的的硬件实现，文献[8]中的设计则采用串行电路结构，资源消耗相对较低，两种设计将会有不同的应用领域。

4 结果分析

在Vivado2016.4软件平台上进行硬件代码设计，然后在Kintex-7 KC705 FPGA开发板上进行板级测试，对应的参数n=128,q=65 537，测试最高频率可达330 MHz，仿真测试图如图4所示。

图4 本设计仿真测试Fig.4 Simulation of the proposed design

本文还编写了MATLAB测试脚本来测试代码结果数据的正确性，经过测试，FPGA硬件输出数据正确，所得波形与预期一致。

在Vivado软件中综合实现后，电路的资源消耗报告如表2所示。由表中数据可以看出，本文设计的多项式乘法器的结构资源消耗较少，只用了461个Slice。这是因为一个Slice含有4个LUT和8个FF，所以设计中大量消耗LUT资源是不明智的。本文的设计最高频率可达330 MHz，而且完成一次环多项式乘法只需要1 358个时钟周期，即完成一次多项式乘法需要4.12 μs。

对比表中文献[7]的实现，同是NTT乘法实现，本模块使用了两个NTT和两个PE，使得乘法处理速度大大提高，并且优化了部分结构的设计，使得消耗的Slice数目也相对较少，虽然多使用了一个DSP，但性能比现有文献中的更好。SchoolBook实现消耗的资源数非常少，但是却会消耗大量的时钟数，这是由于它的复杂度是O(n2)，本文设计复杂度为O(nlog2n)，速度比它要快得多。综合来看，本设计在资源消耗不大的情况下，速度(周期)较NTT乘法提高了42%，较SchoolBook乘法提高了92%，资源和性能对比如图5所示。可见，本设计在格密码系统硬件上具有巨大的性能优势。

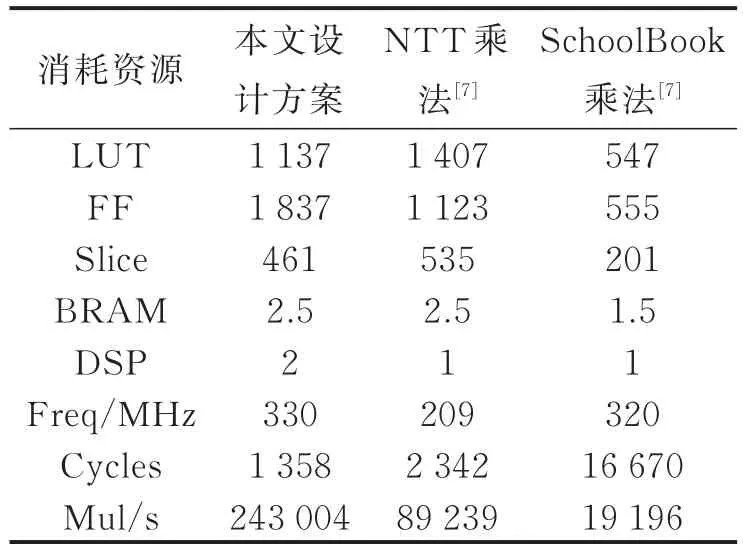
表2 本设计电路资源消耗表Tab.2 Circuit resource consumption of the proposed design

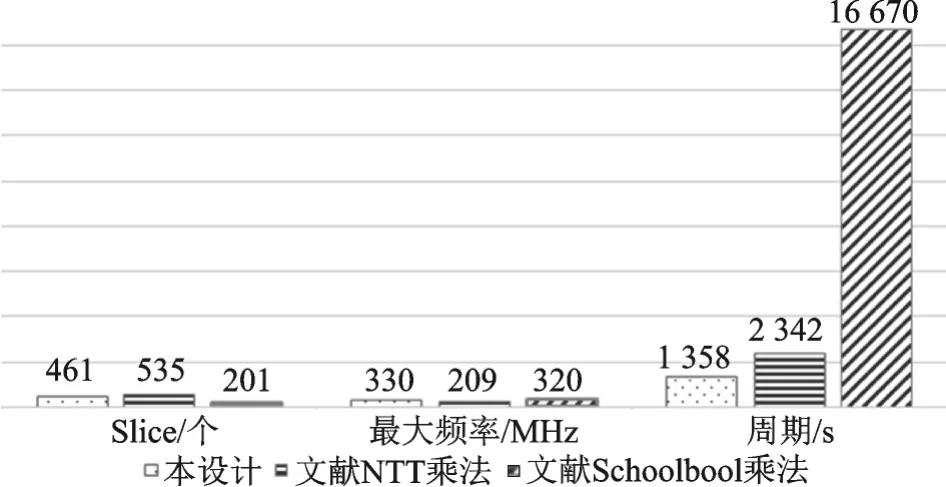
图5 资源消耗、最大频率和时钟周期对比图Fig.5 Comparison of resource consumption,maximum frequency and clock cycle

5 结束语

本文设计采用两个NTT模块和两个PE处理单元的并行电路结构，使多项式乘法的处理速度几乎提高了一半，并且优化了部分结构，使得资源消耗也较少。结果表明，当参数为n=128，q=65 537时，完成一次环多项式乘法只需要1 358个时钟周期，最快只需要4.12 μs即可完成，是一种高速的多项式乘法器设计。因此，本设计能够更好地应用在格密码方案的硬件系统中，有助于提高密码系统的整体处理速度。