基于MSVR的六维腕力传感器静态解耦算法

茅 晨 高 翔 徐国政 宋爱国

（1.南京邮电大学自动化学院，南京，210023；2.东南大学仪器科学与工程学院，南京，210096）

引 言

传感器的感知和反馈是机器人智能化的重要手段之一[1]。六维腕力传感器安装于机器人手腕和手爪之间，用于检测机器人手在作业时与所处外界环境的作用力/力矩的大小及方向[2-4]。由于结构设计的原因，六维腕力传感器存在维间耦合的问题，需要采用合适的解耦算法来消除维间耦合，提高传感器的测量精度。常用的解耦算法有基于最小二乘求解标定矩阵[5]、基于神经网络的解耦算法[6]等。前者容易产生病态矩阵，会导致解耦精度降低甚至导致解耦结果错误[7]；后者容易产生局部极小值从而导致过学习的情况[8]。

支持向量回归机（Support vector regression,SVR）是在统计学理论和最优化理论的基础上发展起来的一种机器学习方法，能够实现结构风险最小化，得到全局最优解，同时避免了神经网络中局部最小值、过拟合的问题[9]。SVR主要应用在模式识别、回归估计、概率密度函数估计等方面[10-11]。对六维腕力传感器进行解耦，即是利用标定的输入输出样本数据对传感器的输出特性进行回归估计的过程。因此，本文提出了基于多输出支持向量回归机（Multi-output support vector regression,MSVR）的六维腕力传感器的解耦算法，并将其应用到实验室研制的六维腕力传感器上。实验结果表明，该算法稳定可靠，能显著提高传感器的测量精度。

1 六维腕力传感器的维间耦合及静态标定

1.1 耦合模型及解耦

理想的六维腕力传感器，每一方向输出通道的电压值仅取决于该方向作用力/力矩的大小，与其余五方向作用力/力矩大小无关。但实际上受传感器的一体化结构设计、机械加工精度、应变片横向效应等因素影响[12]，几乎作用到传感器上的每一维力/力矩分量都会对传感器的各路输出信号产生影响，这就是维间耦合[13]。维间耦合模型如图1所示。

图 1 中，F=(Fx，Fy，Fz，Mx，My，Mz)T为传感器的 6个力/力矩分量输入，U=(UFx，UFy，UFz，UMx，UMy，UMz)T为6路电压分量输出。由维间耦合模型可知，每一路的输出电压值同时受6个方向的力/力矩分量影响。必须对传感器进行解耦，减少维间耦合对测量精度的影响。

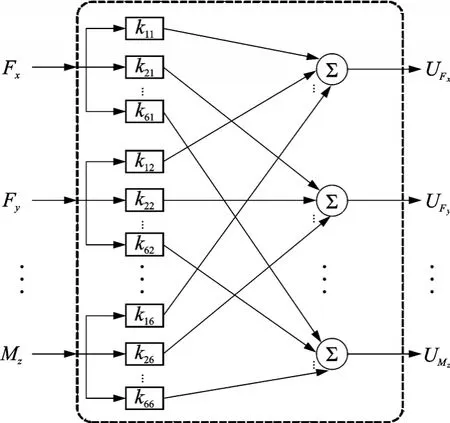
图1 维间耦合模型Fig.1 Model of interdimensional coupling

1.2 静态标定装置与方法

传感器的标定分为静态标定与动态标定[14]。动态标定主要用于检验传感器动态灵敏度、频率响应等动态特性，静态标定主要用于测试传感器静态灵敏度、非线性、静态耦合等指标。本文研究的是多维腕力传感器的静态耦合，因此采用砝码重锤式静态标定方法。其标定装置为本实验室自行研制的如图2所示的加载实验台[15]。

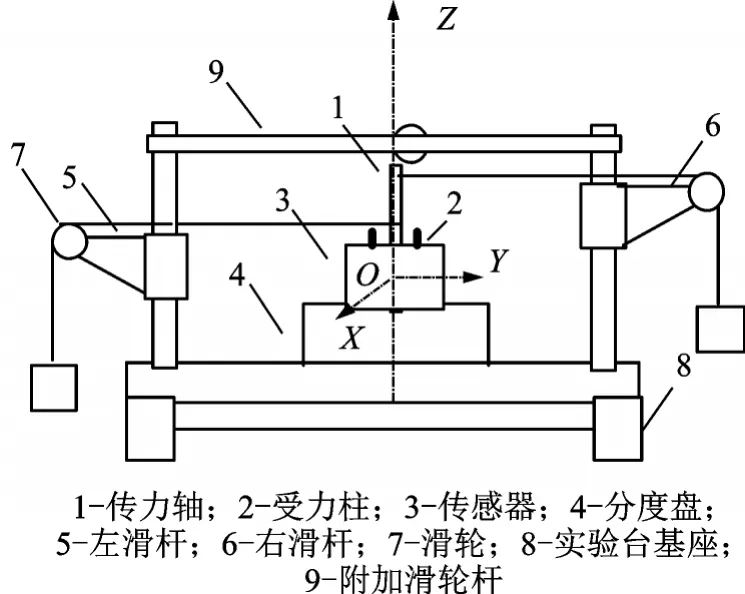
图2 力/力矩加载实验台示意图Fig.2 Schematic diagram of force/torque loading test bench

六维腕力传感器固定在分度盘上，传力轴穿过传感器的中轴线。标定实验中力/力矩的加载方式采用拉力方式，通过调节左右滑杆的上下位置，将砝码的垂直重力转换为水平拉力。利用加载实验台，对六维腕力传感器分别施加三维空间6个线性独立的标准力/力矩分量。实验室研制的六维腕力传感器的满量程范围为：Fx，Fy，Fz方向为-100～100 N；Mx，My，Mz方向为-30～30 N·m。力方向每隔20 N作为一个测量点，Mx，My方向每隔2 N·m、Mz方向每隔1.6 N·m作为一个测量点，各方向载荷从零开始加载至满量程，再逐步卸载至零。每个方向重复标定3次，记录下标定数据。

在每一次标定中，Fx，Fy，Fz方向分别有24个测量点，Mx，My方向分别有64个测量点，Mz方向共有76个测量点，每个测量点包含6路电压输出值和六维力/力矩输入值，这些测量点共同组成一组数据。选择其中两组作为解耦算法的训练数据集；第3组为测试数据集，用来进行误差分析。

2 基于多输出支持向量回归机的解耦算法

2.1 MSVR模型

六维腕力传感器属于多输入多输出系统，基于此特性结合1.1节提出的维间耦合模型，构建了多输出支持向量回归机模型，如图3所示。其中x，y分别为训练数据集的输入和输出，m和n分别为输入输出的维度。该模型将训练数据集空间按照输出维度分割为n个子空间，每个子空间由m维输入和1维输出构成，然后为每个子空间构建1个SVR，用以回归估计对应子空间的输出特性。应用到六维腕力传感器，6路电压分量对应模型中的输入x，六维力/力矩分量对应输出，将这6个子空间的SVR组合即为传感器的全量程输出特性。

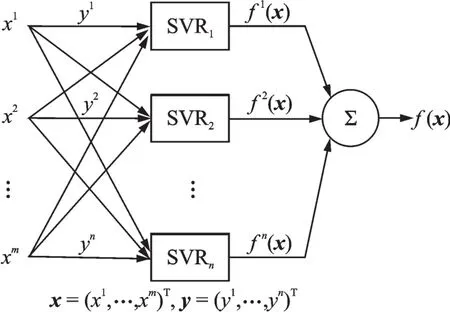
图3 多输出支持向量回归机模型Fig.3 Model of multi-output support vector regression

2.2 MSVR算法

MSVR算法是通过对样本数据进行训练进而得出输入输出关系，实现对输出的预测。对于训练集T={(x1,y1)...(xl,yl)}∈(X×Y)l，其中xi∈X=Rm为输入，yi∈Y=Rn为输出，fk(x)为回归函数，i=1,2,…,l为训练样本数，k=1,2,…,n，m，n为输入及输出变量的维数。采用ε-带损失函数[16]：c(x,y,f(x))=|y-f(x)|ε=max{0,|y-f(x)|-ε}，MSVR要解决的原始最优化问题为

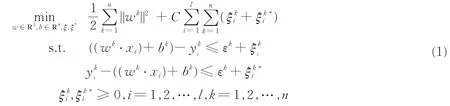
式中：ε=θ-γ为训练时的精度；θ为测试时的精度；γ为损失间隔；C为惩罚参数；ξ,ξ*为间隔松弛变量

引入Lagrange函数[17]，其相应的Wolfe对偶问题为

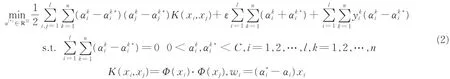
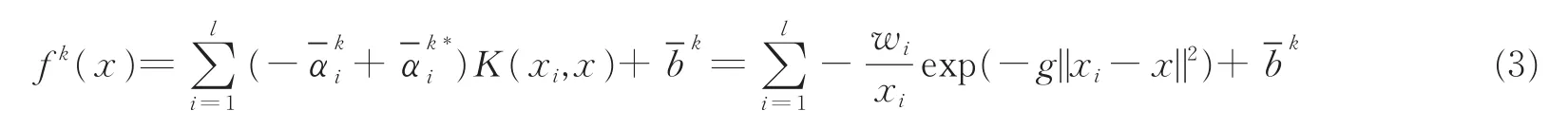
3 算法实现及误差分析

为了测试本文提出的基于MSVR算法的性能，以实验室研制的六维腕力传感器的标定数据作为训练数据集，分别用传统的基于最小二乘求解标定矩阵的解耦算法以及MSVR算法进行解耦，并对结果进行误差分析和比较。两种算法均在MATLAB平台下实现。

3.1 基于最小二乘求解标定矩阵的解耦算法实现及结果

任何加载到传感器上的作用力都能够分解为三维空间坐标系中的3个力分量Fx，Fy，Fz和3个力矩分量Mx，My，Mz，在传感器的载荷范围内主方向的力/力矩输入与电压输出之间是线性关系，且输出电压可以进行线性叠加，则输入输出可表示为

式中：F为6×l力分量矩阵（l为训练数据样本数）；U为6×l电压向量矩阵；H为6×6常数矩阵。

由求解矩阵方程最小二乘估计量的方法求得常数矩阵

在对传感器进行解耦时，自变量为传感器输出的6个电压向量，而作用在传感器上的六维力/力矩分量是未知的，其关系式可表示为

联列式（4，6）可求得

式中C即为标定矩阵，又叫解耦矩阵，是一个6×6的矩阵。求解标定矩阵C的过程实际上就是多元函数最小二乘拟合的过程。为了获得较为准确的标定矩阵，要求标定的测量点数要远大于六维力/力矩传感器的维数。

根据标定得到的训练数据集，利用MATLAB编程，得到标定矩阵C为

3.2 MSVR算法实现及结果

基于MSVR解耦算法的实现步骤如下：

（1）根据1.2节的标定结果，得到训练数据集和测试数据集，将训练数据集和测试数据集进行校零和归一化预处理；

（2）按照输出维度将训练数据集拆分成6个子空间，对每个子空间进行参数寻优，根据训练数据集和得到的最佳参数C，g，依据MSVR算法建立回归模型；

（3）利用回归模型对测试数据集进行输出预测。

各子空间的回归模型及算法评估如表1所示。

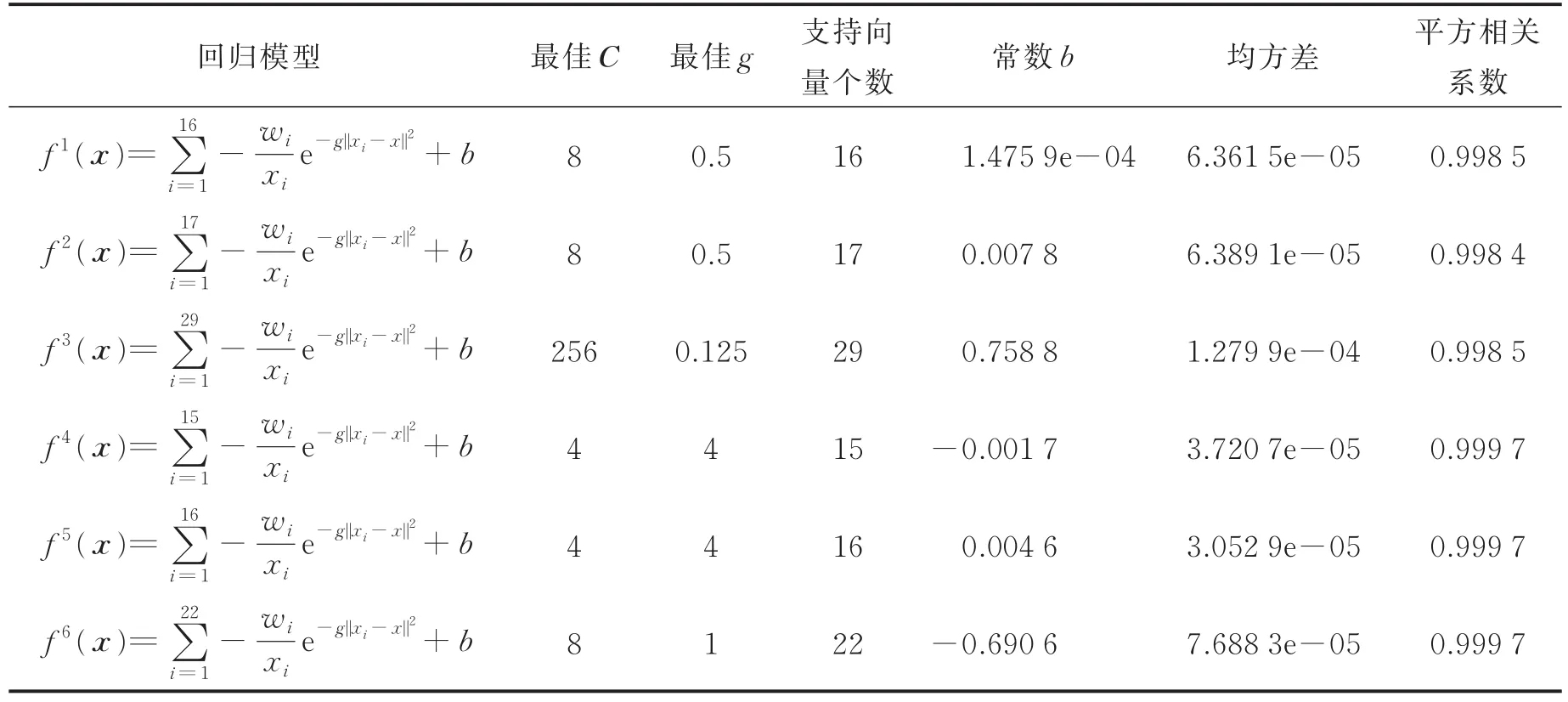
表1 回归模型及算法评估Tab.1 Regression model and algorithm evaluation

3.3 误差分析与比较

传感器的精度指标通常用综合误差（或Ⅰ类误差）和耦合误差（或Ⅱ类误差）[19]来表示

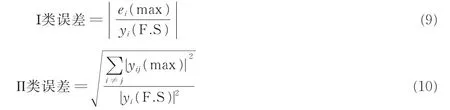
式中：yi(F.S)表示i方向可施加力（或力矩）的满量程值；ei(max)表示i方向实际施加的标准力（或力矩）值与预测得到的力（或力矩）值之差的最大值；yij(max)表示当j方向施加力（或扭矩）值，其他5个方向无力（或扭矩）作用时，i方向预测得到的最大力（或扭矩）值。Ⅰ类误差是反映传感器线性度好坏的指标，Ⅱ类误差是反映传感器各维度间耦合情况的指标。

对第3组测试数据集，分别计算其在未解耦情况下、基于最小二乘求解标定矩阵的解耦算法下（法1解耦）、以及本文提出的基于MSVR的解耦算法下（法2解耦）的两类误差，具体结果见表2。

为保证论文的严谨性，本文利用虚拟样机技术对样机模型进行虚拟标定[20]，获得更多仿真数据在两种解耦算法下的精度对比，使实验结果更具有说服力。具体步骤如下[15]：（1）根据实际传感器参数尺寸，在ANSYS软件下建立三维模型；（2）对模型进行网格划分，划分后的模型共有296 328个节点，200 381个单元；（3）按照弹性体的固定方式，对传感器设置固定约束；（4）对传感器施加满量程范围内的、同实际标定过程中相同的等间距力/力矩加载，以实现实际场景的遍历，根据ANSYS的静力学分析得出各方向应变ε大小；（5）根据式(11)计算各路电压分量大小。

式中：K=2.1为应变片的灵敏系数；E=12 V为应变电桥的供电电压。由此得到虚拟标定数据集，计算在上述3种情况下的两类误差，如表3所示。

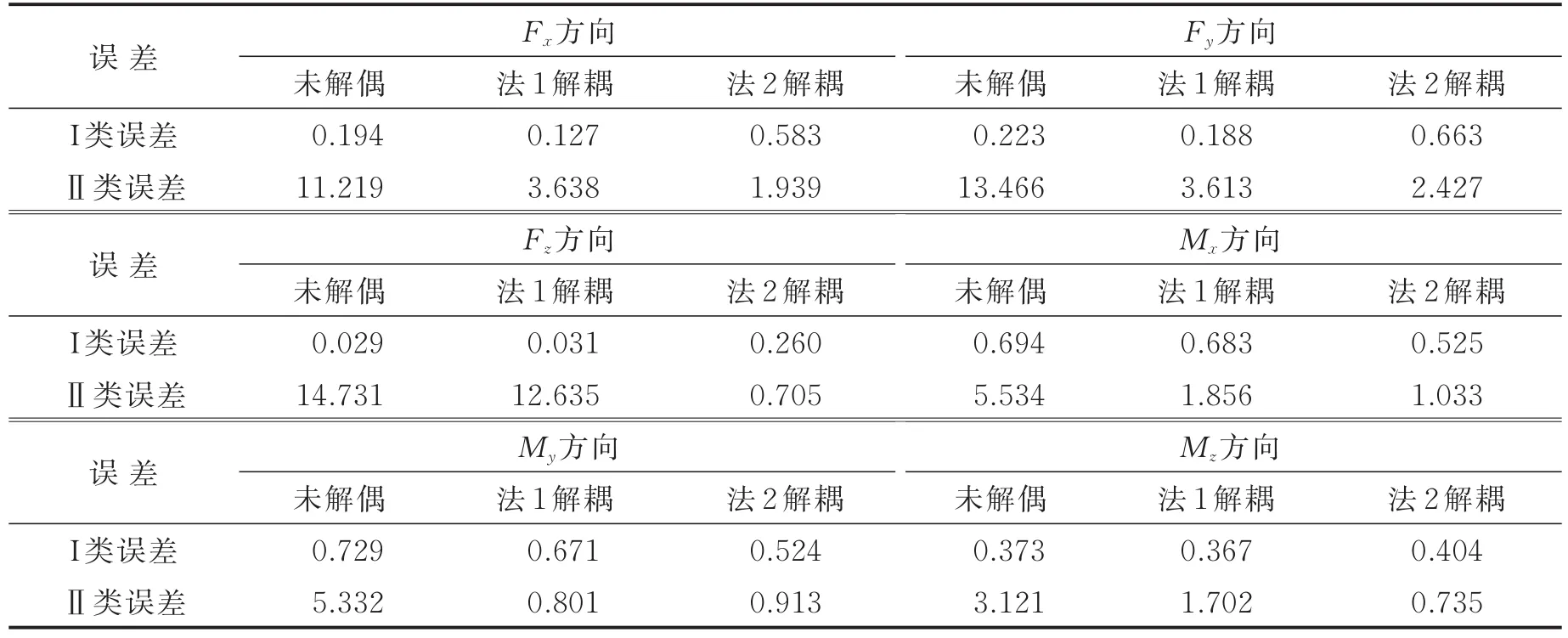
表2 传感器未解偶时以及解耦后的精度对比（测试数据集）Tab.2 Precision comparison before and after decoupling（testing dataset） %

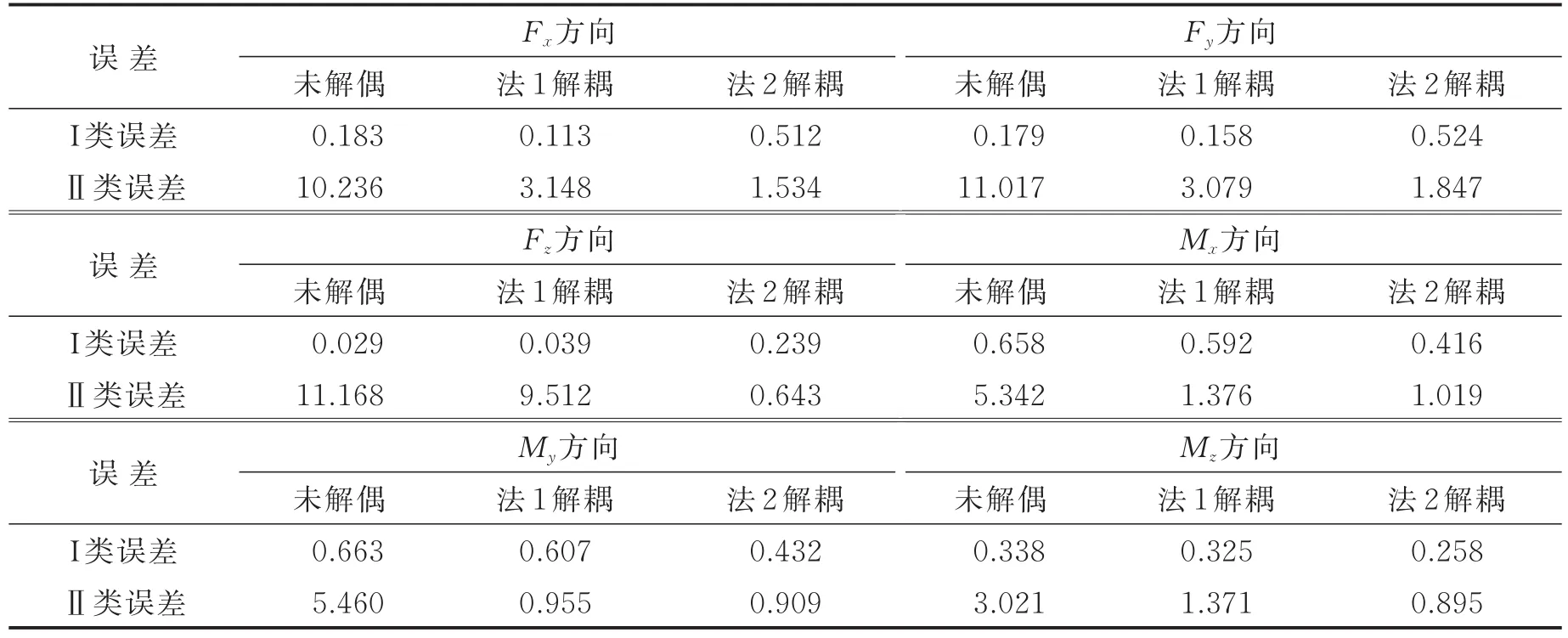
表3 传感器未解偶时以及解耦后的精度对比（虚拟标定数据集）Tab.3 Precision comparison before and after decoupling（virtual calibration dataset） %

分析表2，3可知，由于实验室研制的六维腕力传感器对于主方向有着较好的线性度，在未解偶的情况下，传感器的Ⅰ类误差就比较小，解耦算法很难在此基础上进一步提高精度，两种解耦算法解耦后的Ⅰ类误差都在0.7%以内，因此两种解耦算法对Ⅰ类误差的影响不大。

未解耦时，虽然各方向的Ⅰ类误差很小，但Ⅱ类误差很大，说明维间耦合很大，传感器已不能正常工作。经两种解耦算法解耦后，各方向的Ⅱ类误差有着显著减少，两种解耦算法都能减小维间耦合的干扰。但是从表2，3的数据可以看出，基于最小二乘求解标定矩阵的解耦算法对Fz方向的解耦效果很不理想，解耦后耦合误差依然在9%以上；对其他5个方向的力/力矩解耦效果也一般，耦合误差在0.8%～4%之间浮动。基于MSVR的解耦算法的解耦效果比较稳定，对各个方向的解耦结果较均衡，解耦后耦合误差控制在2.5%以内。

同时，基于最小二乘求解标定矩阵的解耦算法是建立在矩阵方程式求解的基础上，如果在传感器标定实验过程中数据存在粗大误差，或者传感器的电压输出值域空间维数大于施加的力/力矩空间维数时，计算式（7）中的H可能会接近共线性，进而导致HTH成为病态矩阵，造成(HTH)-1中元素取值的极度膨胀，最终影响标定矩阵C的稳健性和精确度。而基于MSVR的解耦算法求解过程中设有间隔松弛变量ξ，ξ*，能有效剔除数据中的粗大误差。

综上所述，基于MSVR的解耦算法解耦效果较好且较为稳定，能有效抑制维间耦合的干扰，具有较高的解耦精度。

4 结束语

本文研究了基于MSVR的解耦算法。以实验室研制的六维腕力传感器为例进行标定并获得标定数据，应用传统解耦算法以及MSVR算法对其进行解耦计算。结果表明，基于MSVR的解耦算法可以避免病态矩阵的产生，具有高可靠性和高解耦精度，可以推广应用到各种维度的传感器的解耦上。该解耦算法已经应用到多种实际工程案例中，例如安装在肌电假手腕部用于感知外界作用力的三维力传感器、具有力反馈功能的远程遥操作手控器、实验舱机械臂六维腕力传感器、人服系统作业能力多维力/力矩综合测试系统等，均取得了很好的解耦效果，满足实际工程精度要求。