一种高效的大监控区域移动目标追踪算法

乐燕芬 盛存宝 施伟斌

（上海理工大学光电信息与计算机工程学院，上海，200093）

引 言

在室内环境下对移动物体进行定位或追踪，是物联网基于位置服务的关键技术之一。由于室内环境或建筑物密集区全球定位系统(Global position system，GPS)信号快速衰减，定位能力受制，因此国内外的研究人员提出了多种不同的技术方案，如基于红外信号[1]、超声波技术[2]等来实现室内定位，定位精度较高，但需要视距传输和专门的硬件设施，在大规模部署时有局限性。微软研究院在2000年公布了基于无线局域网(Wireless area networks，WLAN)的RADAR定位系统[3]，随着无线局域网的快速发展，基于WLAN的定位技术受到研究人员的青睐，成为实现室内定位的重要研究方向，其中基于位置指纹库的技术成为主流[4-10]。由于无线接入点(Access point，AP)发射的信号强度与距离的非线性及强时变性，这类方法或着眼于减小有效搜索区域、提高指纹匹配效率[5-6]，或致力于提高匹配的精准度[6-10]。随着射频技术和嵌入式系统的发展应运而生的无线传感器网络（Wireless sensor networks，WSNs）通常由大量低功耗的分布式传感节点协同工作，来完成网络控制、环境监测、目标定位与跟踪等诸多复杂的任务。在很多应用中，传感数据必须携带位置信息才有意义，因此实现传感器节点的自定位成为提供监测目标信息的必要条件。如何设计稳定、高精度的定位算法也成为WSNs研究中的热点问题之一。在众多的算法中，基于接收信号强度指示（Received signal strength indicator，RSSI）的定位技术由于无需增加额外的硬件设施而受到较多的关注[11]。Sandy等[12]利用移动目标接收的RSSI值，采用基于核函数的岭回归算法从指纹数据库中找到匹配的参考位置点，然后再利用卡尔曼滤波进行位置估计完成追踪。这种算法定位精度较高，但它利用机器学习的方法完成指纹匹配，涉及大量的计算，不适合某些利用运算能力有限的节点比如智能移动终端来实现追踪的应用。石欣等[13]基于监控区域内，参考节点之间以及参考节点与移动节点之间通信的RSSI构建相异性矩阵，采用多维度标度法求解节点位置。该算法鲁棒性强，对RSSI扰动相对不敏感，但在实施过程中利用粒子群算法优化参数，减小坐标转换误差，运算量较大；同时根据实际应用环境，需首先建立参考节点的RSSI相异性矩阵，进行算法模拟获得相异性修正指数，在大监控区域内，这个参数如何选取还值得进一步研究。

考虑某些对位置隐私的应用，通常由终端设备完成自身定位或追踪，并综合考虑跟踪精度、算法复杂度和存储容量等因素，本文提出了适合锚节点稀疏分布的大监控区域，基于位置指纹库的局部加权K-近邻算法(Local weighted K-nearest neighbor，L-WKNN)完成移动目标的初步定位，再利用卡尔曼滤波融合目标加速度信息完成追踪，对算法的性能进行分析，并比较一阶和二阶卡尔曼滤波模型对定位精度的影响。

1 基于RSSI的高效追踪算法

1.1 基于位置指纹的定位算法

RSSI定位的基本思想是未知位置的移动物体/用户（也称盲节点），通过测量接收到的位置确定的参考节点（也称锚节点）所发射信号的强度来估计自身位置。实现方案主要有两类：一类是利用射频信号传播模型确定RSSI值与信号传播距离之间的关系[14]，再利用几何方法，如三边测量、三角定位等估计移动目标的位置，其定位精度依赖于信道传播模型的精确度，而在室内环境下，人员活动频繁、布局室内差异等使RSSI值多变，定位效果不佳；另一类定位算法可称为位置指纹匹配算法。这类算法充分考虑实际检测环境的静态特性，并体现在指纹信息中。通常定位过程分为离线指纹数据库构建、在线指纹数据匹配两个阶段。在第1阶段需要将待定位区域划分多个参考点，并采集每个参考点接收的锚节点的RSSI值作为指纹信息，得到充分描述该区域的RSSI特性指纹库；在第2阶段移动目标获取锚节点的RSSI值，并与参考点的指纹信息匹配，估计自身位置。常用的匹配方法包括最近K-近邻算法、加权K-近邻算法等[7-8]。这些算法简单、易实现，但射频信号的衰减与传播距离并不是线性关系且易受环境干扰，使得测量RSSI值存在不确定性和高非线性，因此基于欧式距离的指纹匹配算法定位精度不高。

为提高匹配精度，近几年也有文献采用基于机器学习的神经网络，支持向量机(Support vector machines，SVMs)[8]、岭回归[6,11]、核函数[7,9-10]等方法对监控区域参考位置的RSSI分布进行建模，但这类方法不仅离线训练阶段的建模过程涉及大量数据运算，在追踪过程中完成指纹动态匹配同样如此。如文献[10]所提出的基于核函数特征提取的定位方法，在追踪阶段采集的指纹信息需经过KPCA变换获得特征向量，变化过程中指纹信息需与指纹库中所有特征位置指纹进行高斯核函数运算，并通过计算与库中每个特征指纹的欧式距离判断其相似程度，这在目标监控范围广、锚节点布局数量多、网格分布密集时，计算效率不高，也限制了其在某些应用场合，如需要利用移动终端实现多目标实时追踪时的应用。

不同于上述方法，本文综合考虑定位精度和计算效率，针对大监控室内区域下移动目标，如四轴飞行器、无人机的追踪，提出了一种新的算法。该算法结合指纹地图和加速度信息，采用一种改进的加权K-近邻算法和卡尔曼滤波实现对移动目标的实时追踪。

1.2 局部加权K-邻近定位算法L-KWNN

假定在某二维监测定位区域内，布置了Ns个锚节点，每个锚节点的位置已知，可表示为Si=(Si1,Si2)T，i∈{1,…,Ns}。整个监测区域可随机或网格状构建N个指纹，也即N个参考位置点，表示为Pl=(Pl1,Pl2)T，l∈{1,…,N}。这N个参考位置点的物理位置信息构成位置空间P=(P1，P2，…，PN)T。锚节点以确定的发射功率持续广播，在每个参考位置点进行若干次信号采集，将RSSI均值作为参考位置点Pl的指纹信息，可表示为一个Ns维向量ρl=(ρ1l, …,ρxl, …，ρNsl)T，l∈{1,…,N},其中，ρxl是来自第x个锚节点的RSSI均值。若采用位置模型建立指纹库，可以获得N个训练集{ρl,Pl}，l∈{1,…,N}。离线训练阶段就是要找到最佳的变换函数Ψ(·)，对每一组输入的RSSI值ρl确定相应的参考位置Pl。确定Ψ(·)后，在线定位阶段移动节点利用变换函数，由RSSI值估算自身位置。

本文算法并不采用上述复杂的模式匹配方法完成指纹匹配，而是采用一种改进的K-近邻算法L-KWNN完成目标节点的粗定位，具体如下：设某移动节点在大监测区域内自由活动，在k时刻的位置表示为x(k)=(x1(k)，x2(k))。追踪时，移动节点以固定时间间隔接收来自锚节点的信号，在k时刻的RSSI向量用ρk=(ρ1,…，ρNs)T表示。考虑到锚节点布局稀疏，至少间隔10 m以上，环境变化引起的RSSI波动会增大实测的RSSI向量与指纹的欧式距离，但基本不会改变对应的锚节点信号强度的分布趋势，也就是即使扰动存在，改变某1,2个锚节点的强度变化趋势，但传输距离越远信号衰减越多这个总体的趋势并不改变。基于这一点，本文算法的步骤如下：

（1）完成局部锚节点匹配。以RSSI值的大小对锚节点进行删选，从ρk的Ns个RSSI值中选出信号强度最大的Nk个，并确定其所对应的锚节点物理位置作为局部匹配锚节点。

（2）确定待匹配指纹。指纹库中位于局部匹配锚节点周围一定区域内的N′个参考位置点作为待匹配的指纹。

（3）找到n个匹配指纹。计算ρk与N′个参考位置点指纹信息ρi的欧式距离

式中(ρk,ρi)可以表征ρk与ρi间的相似程度，其值越小，二者越相似，也可认为k时刻移动节点与对应参考位置点越接近，位置估算可靠性强。对这N′个进行排序，选出前n个最小的及其对应的参考位置点Pi作为匹配集I(k)。

（4）估算位置。移动节点在k时刻的位置可以用式（2）估算

式中：Pi为所选参考位置点的坐标；wn为归一化的权重系数，表征该参考位置点对估算位置的影响度，可表示为

根据以上算法描述，可以得出L-WKNN算法的优势如下：

（1）算法在离线阶段只需采集每个参考位置点的RSSI值，构成指纹数据库，并不需要在更高维度进行特征提取，离线阶段涉及的训练工作量小。

（2）算法在追踪过程中，对获得的指纹数据并不进行全局匹配，而是首先获取移动节点最邻近的若干锚节点，再对锚节点一定物理范围内的参考位置点进行匹配，寻找最接近的n个位置，通过加权平均后作为移动节点的估算位置。由于本算法的应用场景为大监控区域的移动追踪，锚节点布局是物理间距在十几米到几十米的范围内。虽然RSSI值在采集过程中由于室内环境的复杂性会存在干扰，一般测量值会存在10 dBm的误差，对应的距离为2～4 m，这并不影响锚节点的选取。另外，由于锚节点分散分布，即使室内环境局部突变引起干扰增强，其对RSSI的影响一般也只局限于某一个锚节点，不影响其他锚节点的选取，因此这种局部匹配法在提高计算效率的同时并不会引入大的定位误差。

1.3 追踪算法

基于位置指纹获得的节点位置，通常定位精度不够高。通过对移动节点运动状态的分析，建立合适的模型，采用卡尔曼滤波可以提高定位精度，很多文献对移动节点的定位或追踪采用了这一方法。本文根据移动节点的运动状态，采用一阶和二阶模型[12]对其追踪性能进行仿真分析。

假设移动节点携带有加速度传感器，在二维监控区域内运动，每个节点独立追踪。为表述简单又不失一般性，本文估计某个节点在当前k时刻的坐标位x(k)，采用线性模型描述节点的运动

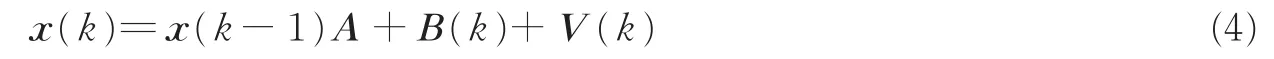
式中：x(k-1)为节点前一时刻的位置；A为2×2维的状态转移矩阵；B(k)为取决于加速度的输入控制量；V(k)为随机噪声，一般可认为是均值为0，协方差矩阵为Q(k)的正态分布，即V(k)～Ν(0,Q(k))。节点在运动过程中，与锚节点通信，并获得一些测量值z(k)。这样，观测方程就可描述为

式中：H为观测矩阵，该矩阵描述了状态量x(k)与观测量z(k)之间的关系。n(k)～Ν(0,U)为观测噪声，符合均值为0，协方差矩阵为U的正态分布。若定义了状态空间模型和观测方程，基于测得的加速度信息，可以由前一时刻位置x(k-1)预测当前位置x(k)。一阶模式下，在连续的两个采样间隔内，假设节点速度保持恒定；二阶模式下则认为在采样间隔内，加速度为常数，而速度则线性变化。不管哪种模式，移动节点的运动均用式(4)描述，两种状态模型具体描述如下。

(1)一阶状态模型

该模型认为开始追踪前移动节点静止，也即v(0)=0。追踪开始后，节点速度按式(6)进行更新计算

式中a(k)为在k时刻采集的加速度。由于设定k-1时刻到k时刻速度近似恒定，因此式(4)中

而A是2×2的单位矩阵，这也意味着此模型适合加速度较小的移动物体，在一个采样间隔内，可认为速度变化不大。

模型的位置噪声V(k)由加速度测量误差所引入，可认为符合均值为0，方差矩阵为Q(k)的正态分布，其中

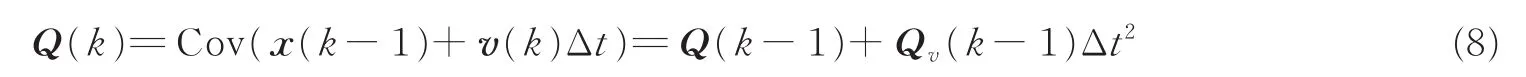
由于初始位置确定，Q(0)=0。Qv(k)为k时刻速度的方差矩阵，符合

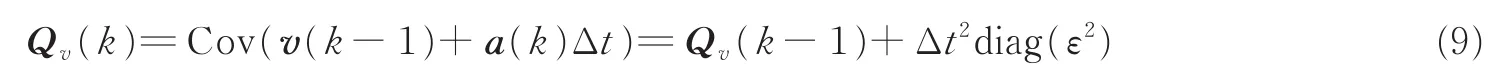
式中：diag(ε2)为2×2的对角矩阵，对角线上的元素εd2，d=1,2，是测得的运动节点加速度的方差，且假设各运动轴方向上的加速度彼此独立。也由于这一点，速度的方差矩阵Qv(0)为对角线矩阵，且有Qv(0)=0。

(2)二阶状态模型

假设节点在时刻k-1与k之间的Δt时间内加速度恒定，表示为a(k)，那么仍采用式(6)估计节点的运动速度，而状态方程的控制量B(k)则符合

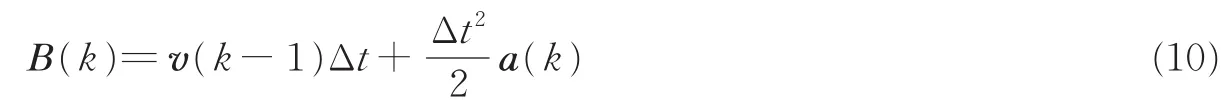
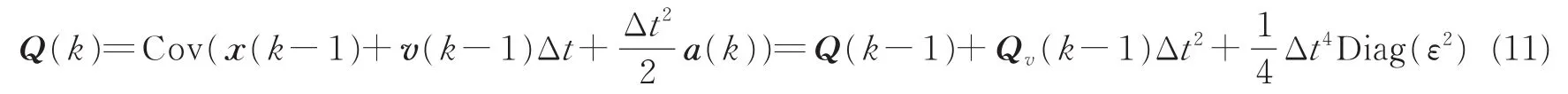
式中：k=0时，Q(k)=0；速度的方差矩阵Qv按式(9)更新。

两个模型的区别在于采样间隔内节点运动是假设为匀速运动还是匀加速运动。对于运动轨迹变化剧烈的节点，显然二阶模型更适合。不管一阶还是二阶模型，涉及的只有简单的迭代运算，所需的计算量都不大。

其次考虑模型的观测方程。在对运动节点追踪过程中，并不是把测量所得RSSI值作为观测方程的观测量，而是利用前述L-WKNN获得的运动节点的估算位置x^(k)作为观测量z(k)，也即

这样，观测方程中的H矩阵可设为单位矩阵，而观测噪声n(k)的协方差矩阵U在跟踪之前需计算确定。可以把节点布置在监控区域的S个确定位置，获得S组{ρl,Pl}，再利用L-WKNN算法估算位置，通过计算实际位置与估算位置的误差获得方差作为观测噪声的方差U。一般可认为该方差矩阵在整个跟踪期间不变，并适用所有的运动节点。

通过以上分析确定了运动节点的状态空间模型和观测方程，接着便可采用卡尔曼滤波的方法解决跟踪问题：首先用k-1时刻运动节点的状态(位置)估计值和状态空间方程来预测k时刻的状态(位置)；然后用观测方程对预测值进行修正获得k时刻的状态估计值。卡尔曼滤波以最小均方误差为估计准则，采用迭代运算对存储空间要求不高，适合传感器节点运算。

状态转移矩阵A为单位矩阵，状态方程中的位置随机噪声V(k)的方差可由式（11）获得

2 仿真分析

为验证本文所提算法的可行性，以及在室内环境下RSSI存在较大波动时算法的鲁棒性，本文采用MATLAB进行仿真实验，分析算法的性能。仿真过程中，主要分析以下参数对算法定位性能的影响：

（1）局部匹配锚节点个数Nk、参考位置点个数N′、最近邻参考位置数n对L-WKNN算法性能的影响；

（2）节点不同运动状况下，一阶、二阶运动模型的定位性能；

（3）RSSI值噪声对本定位算法的影响。

实验采用平均误差来衡量算法的性能，定义如下

式中：Nm为在线估计位置点的个数；Xi为运动节点的实际位置；Xi′为估计位置。

实验仿真场景为100 m×100 m的二维监控区域，均匀布置了25个锚节点和121个参考位置点。每个参考位置点的RSSI值由式(14)给出的Okumura-Hata模型[15]获得

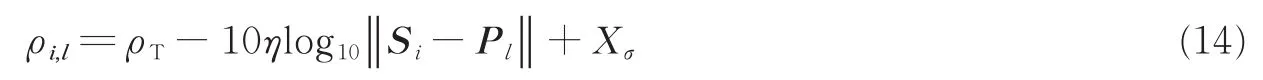
式中：ρi,l为在参考位置点Pl接收到的来自锚节点Si的信号强度，也是参考位置点Pl指纹信息向量中的第i个元素；ρT为初始功率；η为路径损耗因子，根据室内环境的差异，一般设为2～4；‖ ‖Si-Pl为参考位置点Pl与锚节点Si的欧氏距离；由于O-H模型通常适用室外环境，针对室内存在人员走动，多径传播，障碍物等因素，用均值为0、方差为σ2的高斯随机变量Xσ来模拟引起的RSSI值的扰动。仿真参数设定见表1。

表1 仿真参数设定Tab.1 Setting of simulation parameters

图1给出了一个移动节点在监控区域内的运动轨迹，以及基于本文所提出的L-WKNN算法和二阶卡尔曼滤波后的追踪轨迹，采样间隔为1 s，共采集100个点。其各运动轴的加速度如图2所示。在建立指纹库时，每个参考位置点接收到的来自锚节点信号的RSSI值加入了方差σ2为1的噪声，而在在线定位过程中，节点采集的RSSI值加入了方差σ2ρ为16的测量噪声。L-WKNN算法中，选取了接收信号最强的4个局部锚节点，并以这4个锚节点周围20 m内的参考位置点作为加权K-近域算法匹配的位置点范围。本次仿真中选取了4个最近邻的参考位置点加权平均后作为节点运动估计位置，整个轨迹追踪的平均误差小于3.1 m。以此估计位置作为节点运动模型中的观测值，并设两个运动轴的加速度测量噪声误差的均方差ε设为0.01 m/s2，观测噪声的方差U分别设为1.5和2，用二阶卡尔曼滤波进行估计，整个追踪轨迹滤波后的平均误差为1.4 m。

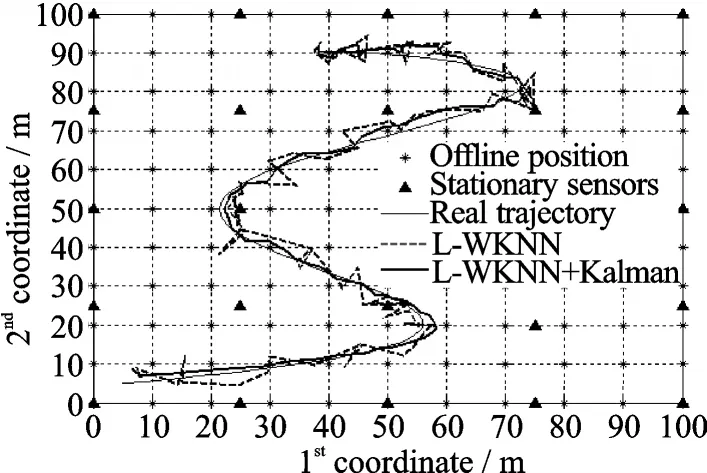
图1 运动节点的轨迹及追踪路径Fig.1 Tracking trajectory of the target

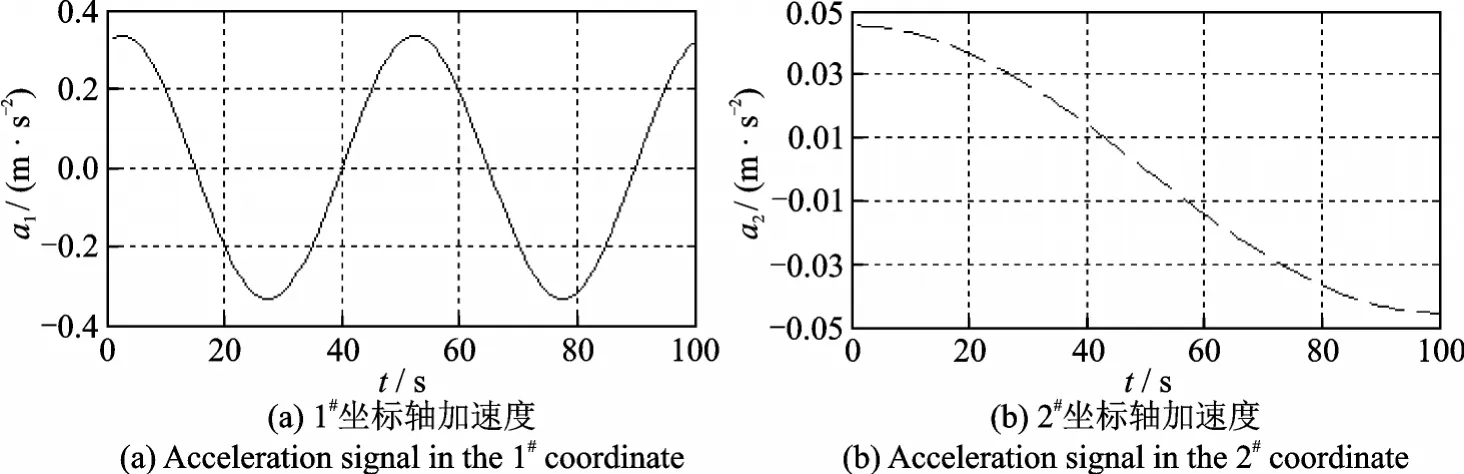
图2 移动节点的加速度Fig.2 Acceleration signals of the target

同时也发现，在RSSI测量方差为16时，本算法与指纹库全局匹配下找到的最近邻指纹一致。图3给出几种算法定位误差的累计密度函数(Cumulative density function,CDF)，其中WKNN与L-WKNN曲线完全重合。网格间距10 m的情况下，采用本算法，90%的定位误差小于3 m。

（1）Nk，N′，n对算法定位性能的影响

Nk为局部匹配锚节点个数，范围在1～Ns之间，随着该值的增加，算法的计算量增大，当Nk=Ns时，本算法退化为普通的加权K-近邻算法；N′为算法所选择进行匹配的参考位置点个数，一般选择局部匹配锚节点某半径范围内的参考位置点，该半径可根据网格的大小进行调整；n为所选择的最近邻参考位置数，在文献中根据网格的大小取值多在4～8范围内。针对图1中的运动轨迹，改变这几个参数值，用L-WKNN算法进行了100次追踪，平均定位误差e及定位误差的标准差σMSE如表2所示。从表2中可看出：适当增大Nk，N′，n有助于提高定位精度，但效果并不明显。在本仿真条件下，也即网格间距10 m，RSSI值测量噪声方差σ2ρ为16时，4个局部匹配锚节点半径20 m内的参考位置点可以有效完成定位，且平均定位误差e说明算法整体定位精度较高，而标准差σMSE表明算法的一致性较好，定位误差波动小。

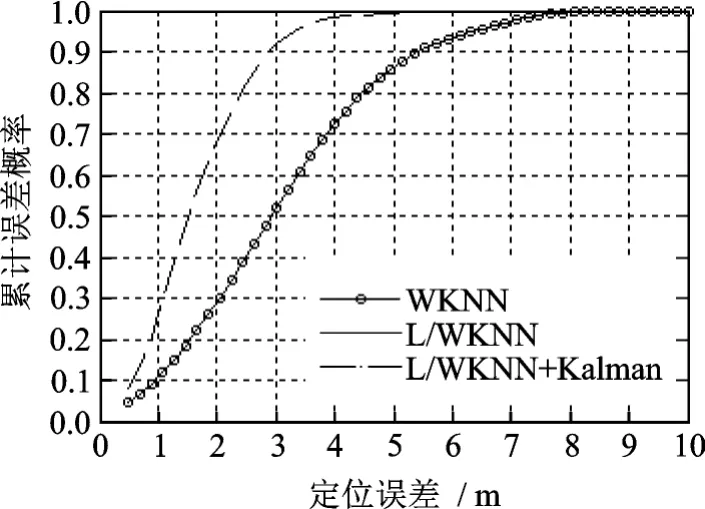
图3 定位误差累计密度函数Fig.3 CDF of the error distance

表2 不同条件下的L-WKNN算法的定位精度Tab.2 Positioning accuracy of L-WKNN with various parameters

（2）测量噪声对算法的影响

在运动节点动态追踪过程中，室内复杂的环境必然会使测量的RSSI值产生干扰。本文用高斯随机变量的不同方差值来模拟RSSI扰动的大小。图4依次取σρ2=1，9，25来分析追踪算法的精度，其他仿真条件设置同图1。从图4中可以清楚看出，当存在较大测量噪声时，L-WKNN的定位误差增大，而经过二阶卡尔曼滤波后，算法依旧呈现良好的追踪性能，定位平均误差在1.5 m左右。

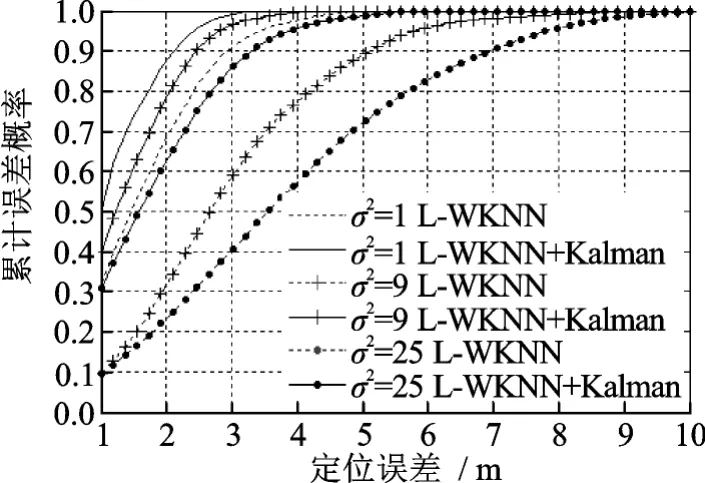
图4 取不同时各算法的定位误差累计密度函数Fig.4 CDF of the proposed methods under differentvalues

（3）一阶、二阶运动模型的性能分析

为研究本文提出的一阶和二阶运动模型对移动节点追踪性能的影响，设置了具有如图5所示运动特点的轨迹，采样间隔为1 s，前55 s内移动节点与图1的轨迹一致，具有变化的加速度，从第56 s开始，节点保持匀速运动。为保证节点一直处于监控区域，共采集了80个采样点。加速度测量噪声误差的标准差为测量值的10%，其他仿真条件设置同图1。图6给出了每个采样点50次仿真的平均定位误差。可以看出，不管运动节点的加速度如何变化，二阶运动模型的定位精度稍高于一阶运动模型，前者的平均定位误差为1.1 m，后者的平均定位误差为1.6 m。

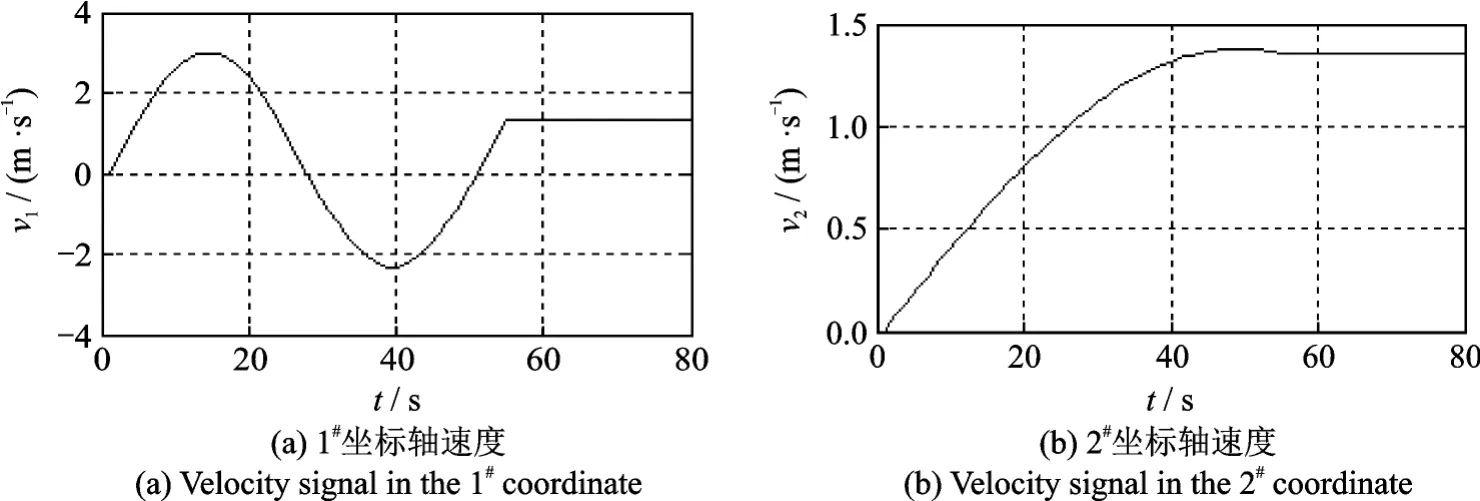
图5 移动节点的速度Fig.5 Velocity signals of the target

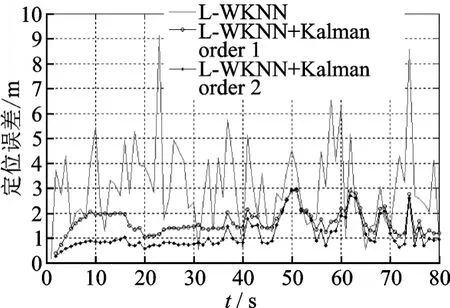
图6 不同算法的定位误差Fig.6 Estimation error of different methods

3 结束语

本文针对锚节点稀疏布局的室内大监控区域，提出了一种基于位置指纹的室内追踪算法。该算法在离线阶段不需要训练建模，在线阶段采用L-WKNN算法，通过寻找局部匹配锚节点大幅缩小待匹配的指纹数量，从而提高计算效率。在追踪阶段，采用融合移动节点加速度信息的卡尔曼滤波提高追踪精度，对一阶和二阶卡尔曼滤波的追踪性能进行了分析。仿真实验表明本算法具有良好的一致性，整体定位精度较高，可有效抑制室内环境变化引起的RSSI测量值扰动对目标追踪性能的影响，适合室内移动目标的实时追踪。在四轴飞行器上对本算法进行性能验证将是下一步研究方向。