基于RLS自适应滤波器的针织圆纬机旋转周期预测方法

刘 涛 谢维波 钟东辉 李自法 谢晓东

（1.华侨大学计算机科学与技术学院，厦门，361021；2.宁德公安消防支队，宁德，352000）

引 言

定量图像分析方法本质上是一种提取关键帧[4]的方法，需要用到针织圆纬机的旋转周期计算出一个周期所需要分析的图片数量，但由于圆纬机在生产中受到使用寿命和运行环境变化等因素的影响，因此造成每转的旋转周期存在极大的不稳定性。为获取较为稳定的旋转周期，本文提出两种方案进行周期预测。方案1为单步周期预测，即采用圆纬机前转周期作为本转的抓拍预测周期。圆纬机运转的前后周期之间存在一定的关联性，在圆纬机稳定运转状态下可以采用前转周期作为本转的预测抓拍周期。但在圆纬机实际生产中，运转前后转的转速存在不稳定性，前转周期作为后转周期虽然相比较固定旋转周期更为灵活，但在预测上依然存在着极大的波动性和不可靠性。为做到本转的预测周期和实际周期的同步吻合，本文提出方案2，即引进递归最小二乘法（Recursive least square,RLS）[5-6]自适应滤波器的方式通过机器自学习圆纬机生产实际周期，来得到接近实际周期的较为稳定的预测周期。

为实现采用RLS自适应滤波器对圆纬机旋转周期的预测，本文建立了用于实际周期采集的硬件模型和软件分析模型的上下位机系统架构，并依据此架构在实际工厂双面针织圆纬机环境上做了大量实验采集实际周期的数据集，最后选取了可靠的数据集在Matlab上实现的RLS滤波器中进行模拟学习和预测分析。研究结果表明RLS滤波器对于预测针织圆纬机旋转周期具有较好的稳定性和收敛性，能够较好地应对针织圆纬机在生产中的突发情况。最后，根据方案1和方案2在周期预测中的不同优势，提出了适用于实时智能疵点检测系统的周期预测处理机制。

1 背 景

1.1 智能疵点检测

在针织圆纬机传统生产中，往往采用人工检测的方式来监控生产中疵点布，但传统方法容易受到检测工人的主观干扰，并且效率低下。伴随工业视频监控的普及和视频图像处理技术的发展，采用基于机器视觉的智能疵点检测的研究越来越多的出现在人们的视野之中。智能疵点检测是对纺织物质量进行控制和实现织造及验布工序自动化、无人化的关键环节[7]，图1给出了针织圆纬机及智能疵点检测模型。以往的智能疵点检测的研究均是围绕着提高疵点检测算法的准确度和降低算法的时间复杂度而进行，然而将算法运用到实际工业生产上依然会受到生产环境的制约。通常的疵点检测系统均采用逐帧分析法实时采集视频图像信息，并对图像信息进行快速的分析来得到分析结果。胚布的疵点信息出现频率低，采用逐帧分析法会浪费大量的图像信息，但使用定量分析方法能够在保障不放过一条疵点信息的基础上大大缩小图像的采集量，同时降低设备的工作负荷，更加适合纺织工业现场。

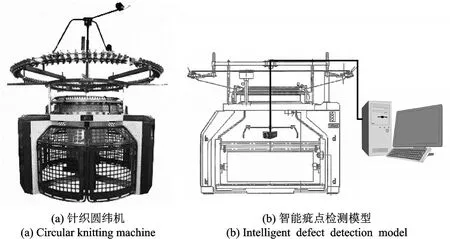
图1 针织圆纬机及智能疵点检测模型Fig.1 Circular knitting machine and intelligent defect detection model

1.2 逐帧分析法

逐帧分析法本质上是等时间差定时抓拍图像分析方法，即在相等时间差上的时刻获取图像帧并对图像进行分析。该方法在视频图像分析中经常用到，使用海康工业阵机进行监控时的帧率设定范围在0～500 Hz，每秒钟可以获取0～500帧图片，对1帧突破性分析处理的所允许的时间不小于2 ms；海康工业阵机默认帧率为48 Hz，每秒钟可以获取48帧图片，处理1帧图片的时间约为21 ms；人眼认为是连续运动[8]的帧率为大于16 Hz，每秒钟可以获取16帧图片，处理1帧图片的时间小于63 ms。

在针织圆纬机工业纺织生产中，每台圆纬机运转速度是根据生产方订单需求和布型要求进行人工设定的，设定范围通常在10～20 r/min，即每转的旋转周期为3 000～6 000 ms。生产中由于圆纬机使用寿命和运行周期等环境的影响，生产前后周期并不完全相等，即存在运转周期的不稳定性问题。如采用逐帧分析法进行图像处理，则必须设定固定帧的方式进行获取图像帧并进行处理。但是伴随着运转周期的不稳定性，这就导致如果设置帧率过大，则采集的图像帧与帧之间的图像重合信息增大，图像处理的时间变短，对图像处理算法的时间复杂度要求变高；如果设置帧率过小，则采集的图像帧极有可能丢掉疵点布图像，导致检测误报率增高。这就为针织圆纬机实时生产中智能检测系统带来了许多麻烦，这也是导致如今的圆纬机智能检测系统一致停留在实验层面而难以应用到工业生产的主要原因之一。

1.3 定量分析法

根据圆纬机在实际纺织生产中疵点布的特征[9]，定量分析法可以很好地解决逐帧分析法中存在的问题，由逐帧法中的固定帧获取改为动态帧获取图像。在理想条件下，定量分析法要求一个圆纬机工作周期内能够确保定量抓拍到的图像可以构成本周内所生产胚布的整体图像。现实生产中，可以根据圆纬机的圆周长度和视频监控视场的大小计算出圆纬机每转抓拍图像的最小量，再由圆纬机的旋转周期固定每个周期内获取图像帧的具体时刻，根据旋转周期范围和抓拍图像的最小量范围可知每帧图像处理的时间范围。在上述最小量范围内尽管依然存在前后帧重叠情况，但相对逐帧法已经大大缩小了图像的重叠信息，达到了图像资源的最大化利用的目的，并且扩大了每帧图像处理的时间范围，允许更多检测率较高但时间复杂度较高的算法进行实时生产检测。在定量分析法中，由于每转的转速存在着运转不稳定状态，视觉监控无法设定固定的旋转周期，从而也就无法精确地捕获本圈布匹完善的疵点图像信息，因而预测准确的旋转周期就变成了分析定量抓拍图像的重点研究对象。

其中用来表示拟合优度的为调整后的判定系数R方为0.975，这说明有97.5%的影响因素可以由此模型来加以解释，相应的各自变量的系数显著性概率值全都小于0.05，所有的T值均大于临界值T（27-3-1）=2.069，表示结果在α=0.05的水平上是显著的。此外，该回归模型的DW值为1.4，说明随机误差项不存在一阶序列相关；AIC值为-0.63较小意味着滞后阶数较为合适。总体表明所建立的回归模型比较好。

2 基于RLS自适应滤波器的抓拍周期预测法

本文中出现的RC,PC,单步PC和N阶PC的解释如表1所示。

表1 本文中自定义名称解释Tab.1 Custom name interpretation in this paper

2.1 RLS算法

自适应滤波器采用RLS算法，根据文献[10]周期预测算法可以按式(1—6)的顺序依次迭代完成。

式中：e(i)为第i次迭代的周期误差，是RLS滤波器的误差反馈信号[11]；RC(i)为第i次迭代的实际周期，用于作为e(i)的第一参数；PC(i-1)为第i-1次迭代输出得到的预测周期，用于作为e(i)的第二参数。

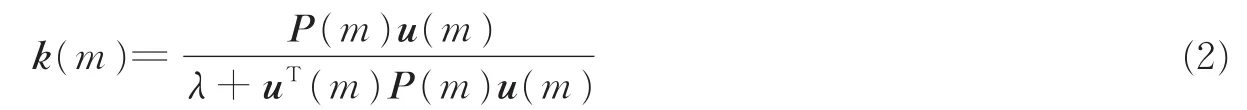
式中：k(m)表示大小为m×1增益向量，通常k(m)值越大，RLS算法的修正能力越强；λ为遗忘因子，相当于LMS算法中的步长，是个常量；m为RLS自适应滤波器阶数。

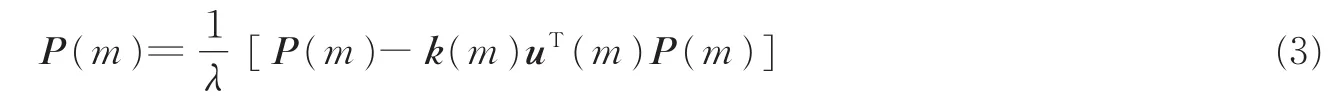
式中：P(m)表示大小为m×m的逆矩阵，需要每次迭代过程中进行更新，每次更新都与第i-1次迭代逆矩阵P(m)、遗忘因子λ以及输入向量u(m)有关。

式中：w(m)表示大小为m×1的权值向量，其向量值是在第i-1次迭代基础上不断累加周期误差e(i)和增益向量k(m)的乘积构成。

式中：u(m)表示大小为m×1的输入矩阵，该矩阵是针对RC进行m阶采样构成，每次迭代都要更新u(m)，更新模式为进出队列模式，每次迭代都要在队头输入一个新的RC(i)，同时将前一次迭代的1到m-1的u向量值向队尾推进。

式中：PC(i)表示第i次迭代完成后得到的预测周期，即RLS滤波器的输出，也将作为第将作为第i+1次迭代求取周期误差e(i)的第二参数，其值为本次迭代的权值向量w(m)的转置向量与m阶输入向量u(m)的向量积得到。

2.2 RLS自适应滤波器周期预测工作原理

根据RLS算法构建出如图2所示的RLS自适应滤波器周期预测的基本原理图，⓪～⑤构成一次迭代过程，迭代过程按照⓪～⑤次序进行，滤波器输入为实际周期RC(i)，输出为预测周期PC(i)。

⓪-①-②过程完成第i次迭代求解周期误差e(i)的任务，过程①的输入信号RC(i)表示为针织圆纬机实际周期,过程⓪的输入信号PC(i)表示为前一次迭代输出的预测周期，RC(i)与PC(i)相减得到周期误差e(i)。

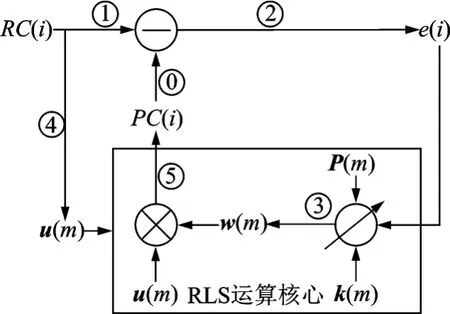
图2 RLS自适应滤波器的周期预测法基本原理图Fig.2 Basic principle of cycle prediction for RLS adaptive filter

过程④完成本次迭代输入向量u(m)的更新，更新模式采用队列模式如图3所示，每次迭代滤波器都会输入一个新的RC(i)，第i次迭代时的RC(i)将作为u(m)的队头(Front)元素进入队列，第i次迭代之前的m-1次进入队列的元素则按照队列顺序依次向队尾(Rear)运动，u(m)将随着迭代的进行不断更新。

图3 更新输入向量u(m)的队列模式图Fig.3 Queue model of update input vectoru(m)

过程③和⑤构建了RLS运算的核心内容，即求解权值向量w(m)和计算预测周期PC(i)。过程③完成本次迭代权值向量w(m)的更新，w(m)是实现RLS自适应滤波器周期预测的关键，RLS自适应滤波器可以根据输入的矩阵u(m)和实际周期数据RC通过自学习不断修正w(m)权值向量，直到w(m)趋于稳定；过程⑤完成本次迭代的预测周期PC(i)输出，其值为权值向量w(m)的转置向量与输入向量u(m)的向量积进行累加得到。

RLS 运算核心如图 4 所示，“1”“2”和“3”分别表示增益向量k(m)、逆矩阵P(m)和输入向量u(m)的更新过程。根据式(2),k(m)更新需要用到本次迭代更新前的输入向量u(m)和逆矩阵P(m)以及遗忘因子λ；根据式(3)，P(m)更新需要用到本次迭代更新前的逆矩阵P(m)和输入向量u(m)，更新后的增益向量k(m)，以及遗忘因子λ；根据式(4)，w(m)更新则需要用到本次迭代更新前的权值向量w(m)、更新后的增益向量k(m)和⓪-①-②过程计算得到的周期误差e(i)；u(m)更新则发生在w(m)更新之后；最后，根据式(6)，完成过程⑤计算得到本次迭代的预测周期PC(i)。

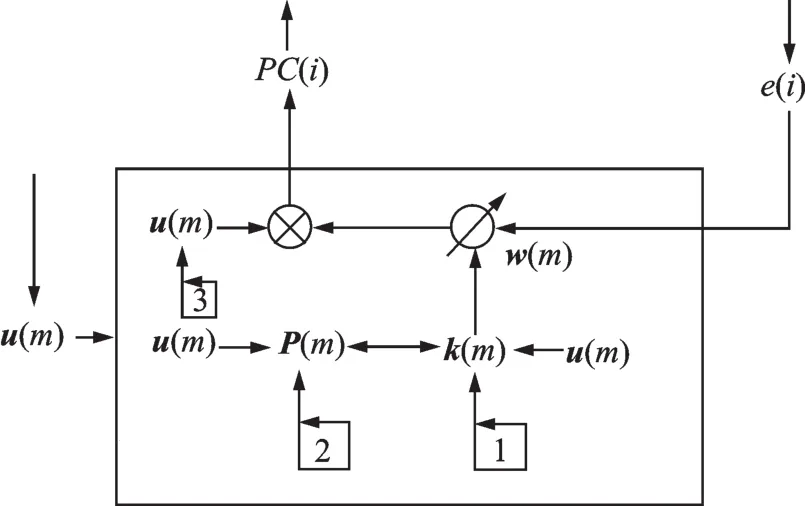
图4 RLS运算核心Fig.4 Computing core of RLS

3 实验分析

3.1 数据获取

在上下位机系统架构（图5）中针织圆纬机、接近开关和接近开关串口信号生成与上传构成系统的下位机，即针织圆纬机的硬件模型；接近开关串口信号分析与RLS滤波器预测分析构成系统的上位机，即针织圆纬机的软件模型。在下位机中“1”和“2”构成一个接近开关，“1”为红外探头，被固定在针织圆纬机机台内壁，“2”为能够阻断红外光线的被固定在能够随针织圆纬机进行圆周运动的圆周外壁螺母。

接近开关信号为9字节串口信号，接近开关信号协议如表2所示，字节信息均采用16进制，即00-FF样式。“字头”采用统一的“005A”信息，确保了设备的统一性和安全性；“设备地址”用户可以根据圆纬机的数量自定义信息，便于统一化设备管理；“命令”统一采用“01”信息，主要是为了区分除去串口信号以外的其他命令信息；“保留”的4字节暂时未作任何处理；“校验和”是前面8个字节信息之和，可用于上位机校验接近开关信号的准确性。

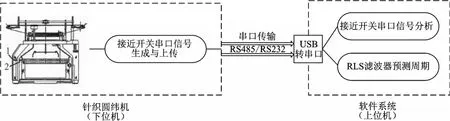
图5 上下位机系统架构图Fig.5 Up-down system architecture

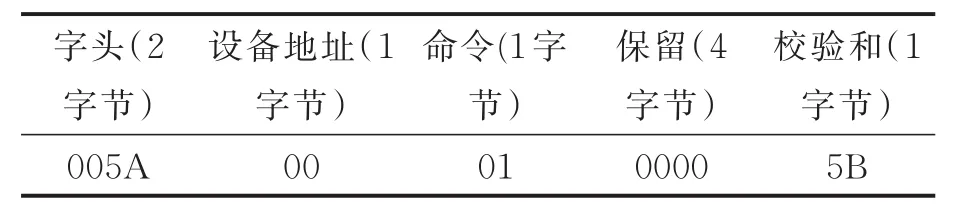
表2 接近开关信号协议Tab.2 Proximity switch signal protocol

针织圆纬机每工作一圈，接近开关均可以产生一个串口信号，并通过RS485/RS232协议上传到上位机，上位机通过USB转串口接收串口信号，进而在上位机上完成串口信号分析，并获取实际周期RC数据集过程,详细的采集数据过程如下。

步骤1接近开关串口信号生成与上传。当“2”接近“1”时能够产生一个9字节接近开关信号，该串口信号可以通过串口传输线（RS485/RS232）再经USB转串口被上传到上位机。

步骤2接近开关串口信号分析。待上位机接收到串口信号之后，要对串口信号进行校验和分析，进而判断当前串口信号是否正确，用于排除下位机因受环境因素干扰上传的错误的串口信号。在接近开关能够正常工作下，当上位机接收到第二个接近开关信号时，即认为针织圆纬机旋转一周，此时上位机可根据接收到的两个接近开关的信号的时间，计算出针织圆纬机经过的一转的旋转周期，标识为RC，并且将当前的第二个接近开关信号作为下一转的的第一个接近开关信号，按照此过程可依次计算出每一转的RC。

步骤3收集并制作RC数据集。根据步骤1和2所述，设计软件工具在真实的纺织工厂的圆纬机环境中进行RC收集，由于在真实纺织环境中，纺织生产作业存在着许多突发因素，如断针、断线和工人手控停机等都会对RC数据集造成不可靠的影响，且对RC数据集的大小造成绝对的影响，本文实验选择在实验圆纬机上进行了多次采集，之后通过对比分析选取了大小为4 578的RC数据集（图6）。

3.2 实验设计

本文设计了未采用RLS滤波器的单步PC和采用RLS滤波器的N阶PC的对比实验，实验平台为Matlab，RLS算法在应用时需要对P(0)进行赋初值。根据文献[12]可知，RLS遗忘因子的取值范围为0.9＜λ＜1，经反复实验，对于任意一组RC数据，设定RLS滤波器λ=0.98，P(0)=(1/λ)×eye，eye表示大小为m×m的单位矩阵。

实验设计分为两部分：(1)寻找RLS滤波器最佳阶数实验；(2)单步周期预测与RLS滤波器N阶周期预测对比实验。实验数据均为大小4 578的实际周期RC数据样本。

为寻找RLS滤波器最佳阶数，设计RLS滤波器误差权重（Power）随阶数N变化的实验。误差权重（Power）采用周期误差e(i)的平方数表示，即Power=e(i)×e(i)。阶数N人为取值2到30。设计4 578次RLS自适应滤波器的迭代过程，伴随迭代的进行，e(i)将趋于平稳状态，再计算出Power值，根据阶数N的不同取值重复上述迭代过程，可获取误差权重Power与阶数N的关系图。

在单步周期预测与RLS滤波器N阶周期预测对比实验中，单步周期预测是将第i次迭代的实际周期RC(i)作为第i-1次迭代的预测周期PC(i)，最终获取4 577组预测周期；RLS滤波器的阶数可以通过实验(1)选取最佳阶数，然后根据RLS自适应滤波器周期预测工作原理在Matlab平台上设计程序，测试RC数据集，获取4 579组预测周期。

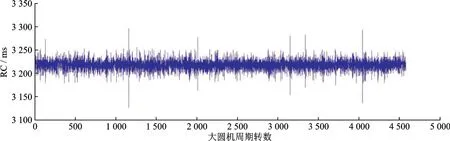
图6 实际周期(RC)数据样本Fig.6 Real cycle(RC)data sample

3.3 实验结果与分析

图7给出了LS滤波器误差权重（Power）随阶数N的变化分布图，由于1阶PC可近似看作单步PC，故而在分布图并未给出1阶PC。从图7可以看出，伴随着N的增长，Power值呈现先快速下跌、再缓慢上涨的分布情况，在N=16时得到Power的最小值，即认为RLS滤波器的最佳阶数在16阶，即m=N=16。实验(2)即是在16阶RLS滤波器上进行的。

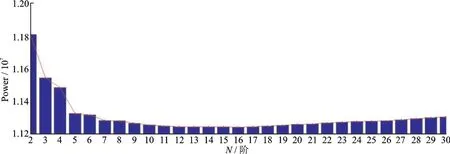
图7 RLS滤波器误差权重分布图Fig.7 RLS filter error power distribution

图8（a）和图8（b）分别表示单步PC（蓝）与16阶PC（绿）和RC（红）的对比实验结果。从图8（a）中能够观察到：蓝色区域覆盖红色区域，RC波动存在偶然性的背离状态，并且在背离处存在着单步PC与RC严重背离的波动。从图8（b）中能够观察到：在300左右个周期之前绿色波动完全包裹红色波动，在300左右个周期之后转而红色波动包裹绿色波动，同样RC波动存在偶然性的背离状态，但是不存在图8（a）中出现的背离现象。通过图8（a）和图8（b）的比较分析发现，16阶PC可以有效地避免单步PC中出现的偶然性严重背离现象，但这也仅限于经过300左右个周期之后，在300左右个周期之前其预测效果弱于单步PC。

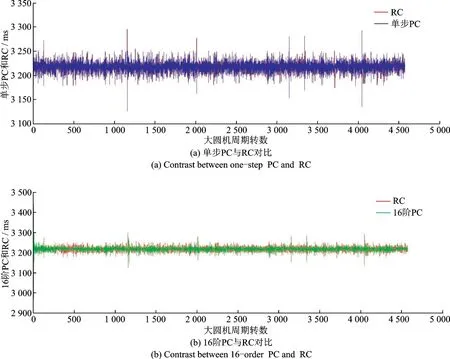
图8 单步PC、16阶PC与RC的对比Fig.8 Contrast between PC of one-step or 16-order and RC

为了更加直观地比较分析单步PC和16阶PC的预测效果，对单步PC（蓝）与16阶PC（绿）进行误差对比，结果如图9所示。通过比较分析可得到如下结论：在300左右个周期之前绿色波动覆盖蓝色波动，并且绿色波动存在偶然性的背离状态，说明在300左右个周期之前16阶PC与RC的误差值较高，16阶预测效果较差；在300左右个周期之后绿色波动反被蓝色波动包裹，并且蓝色波动出现偶然性背离状态的地方，绿色波动并未呈现同样的状态，且波动状态较为稳定，说明在RLS滤波器在经过300个周期左右的学习后，预测效果趋于稳定，并且稳定性要远优于单步PC。

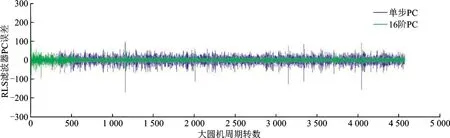
图9 单步PC与16阶PC误差对比Fig.9 Error contrast between one-step PC and 16-order PC

通过上述实验分析可知，采用16阶RLS滤波器能够有效地预测周期PC，但在预测到稳定的PC之前需要经过一个300左右的缓冲期对向量权值进行自学习的过程，故而在实际针织圆纬机生产过程中，可在智能疵点检测系统中设置如图10所示的智能疵点检测系统PC预测处理机制，即设立RLS滤波器缓冲期和RLS周期预测期，其中RLS缓冲期由单步PC构成，RLS预测期由16阶PC构成。

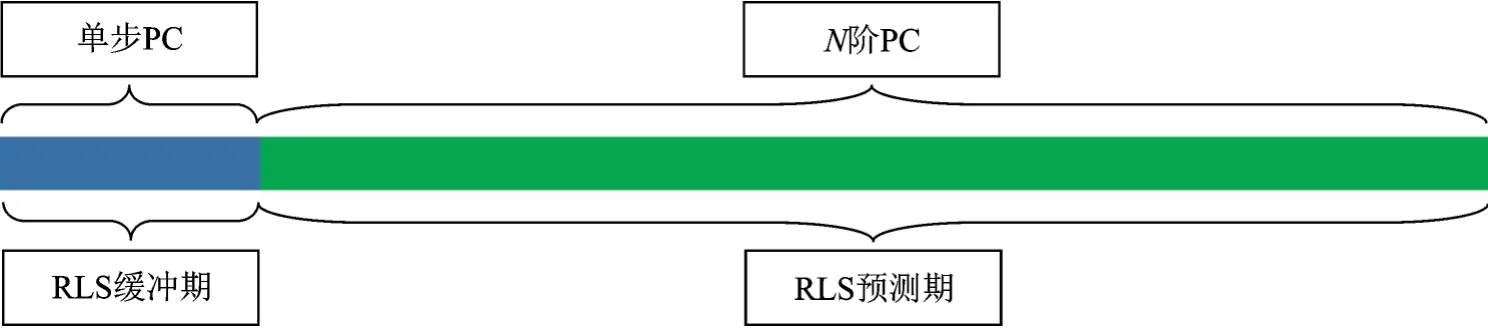
图10 智能疵点检测系统周期预测处理机制Fig.10 Cycle prediction processing mechanism of intelligent defect detection system

4 结束语

本文将RLS自适应滤波器用于针织圆纬机旋转周期预测，分析了RLS滤波器的基本工作原理，搭建了采集旋转周期数据集的上下位系统架构，并利用上下位系统在针织圆纬机上采集了实时工作的实际周期数据，最后在Matlab平台设计了两个实验：（1）寻找RLS滤波器最佳阶数实验。结果表明，能够通过RLS滤波器准确找到在针织圆纬机上进行RLS周期预测的最佳阶数。（2）单步周期预测与RLS滤波器N阶周期预测对比实验。实验表明，相对于单步周期预测，RLS滤波器能够在确认阶数的基础上得到较为稳定的周期预测结果。为解决缓冲期在智能疵点检测系统周期预测中的限制性，本文结合单步周期预测和RLS滤波器N阶周期预测的不同特性，得到了智能疵点检测系统周期预测处理机制。