基于DHMM的低心率变异性心音的分割方法

许春冬 周 静 应冬文, 侯雷静 龙清华

（1.江西理工大学信息工程学院，赣州，341000；2.中国科学院声学研究所语言声学与内容理解重点实验室，北京，100190）

引 言

随着社会生活的不断复杂化，心血管疾病的患病率逐年上升，已经成为全球慢性病的主要致死原因之一[1]。在心血管类疾病的诊断中，常用的方法包括血压检测[1]、心电分析[2]、心脏超声检查[1-2]、冠状动脉CT[1]、心肌灌注同位素图像法[3]和心音分析[1-3]等。其中心音分析不仅可以检测出受试者是否存在异常，还可通过其作出病况预测，且方便、快速、经济，是一种完全无损的检测方法。心音分析已经得到了广泛应用，并成为心血管疾病主要的辅助诊断方法之一。

心音信号由心脏机械工作产生，其蕴含着丰富的生理与病理信息。心音分割是心音自动分析的主要步骤之一。心音周期性分析及分割的根本目的是通过提取各心音成分上的病理特征，使后续的心音分类及诊断目标性更强、准确度更高。现实中，心音极易受到临床环境噪音、体内杂音、信道差异、以及心率波动等因素的影响，这使得分割过程变得十分困难。

现阶段主要的分割算法包括基于包络的分割方法[4]、基于特征提取分析的分割方法[5]、基于机器学习的分割方法[6]、基于隐马尔可夫模型（Hidden Markov model,HMM）的分割方法[7-9]。其中基于HMM的方法能够通过观察值序列和隐含状态序列间的关系反映出的随机过程判断出存在的合理状态序列，这种特点使HMM在心音分割处理中得到了一定深度的研究。HMM在语音活动性检测中已经得到了深入的研究，但在心音定位分割及分类领域，从模型建立和分割精度要求角度来看，还存在一定的研究空间。现阶段基于HMM的分割算法多是通过大量训练集进行的非监督学习，容易造成模型泛化而无法保证提取的信号特征的与信号的高度匹配，会丢失部分细节特征，从而使得对目标信号的分割精度下降。因此，结合HMM在心音分割中的研究现状，本文采用基于时间相关性的隐马尔可夫模型（Duration-dependent hidden Markov model,DHMM）探求精度更高的分割算法。

1 心音成分及分割任务要求

心音一般是指由心肌收缩、心脏瓣膜关闭、血液撞击心室壁和大动脉壁等活动引起的振动经胸腔、胸壁等组织传导至体表所产生的声学信号[10-11]，是能够反映人体心脏及心血管系统机械运动状况的信号之一[12]。心脏结构如图1所示，心脏通过循环的收缩活动来为人体不断输送血液，其活动状态为一周期过程。对于正常人而言，心音信号近似于准周期信号，每个周期约在600 ms～1 s之间[2]，医学上称作心动周期。每个心动周期内可包含4个心音成分[1,3,7]：第1心音（s1）、第2心音（s2）、第3心音（s3）和第4心音（s4）。一般s1和s2极易被听到，而s3和s4主要出现在特定人群的心音中，如s3主要出现在儿童心音信号中，s4主要出现在一些病理心音信号中。在医学上，常认为一个心动周期由s1，收缩期，s2和舒张期4个部分构成，且在任意一个心动周期中均存在，出现顺序是固定循环的，如图2所示。

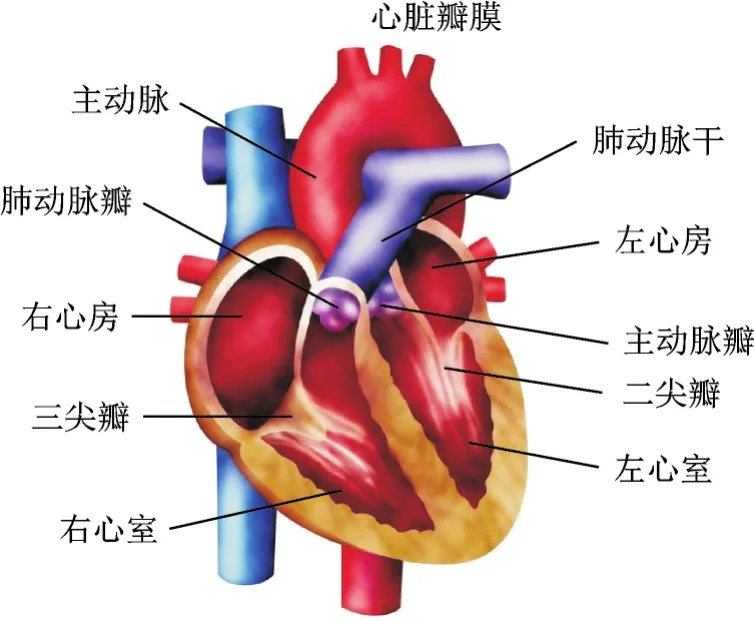
图1 心脏结构Fig.1 Structure of the heart

医学上将s1和s2称作基础心音（Foundamental heart sound,FHS）[2,5,8]。心音分割的主要任务是精准有效地将各心动周期划分为s1，收缩期，s2及舒张期，以达到有效提取各心音成分特征参数的目的。此外，心音分割可为后续的模式识别（分类）工作提供定位基准，是实现瓣膜病、心率衰竭和冠心病等疾病无创、快捷诊断的前提与基础。心动周期分割的有效与否，将直接影响到整个心音分析系统的精准性，因此，在心音自动分析处理中，分割步骤极为重要。

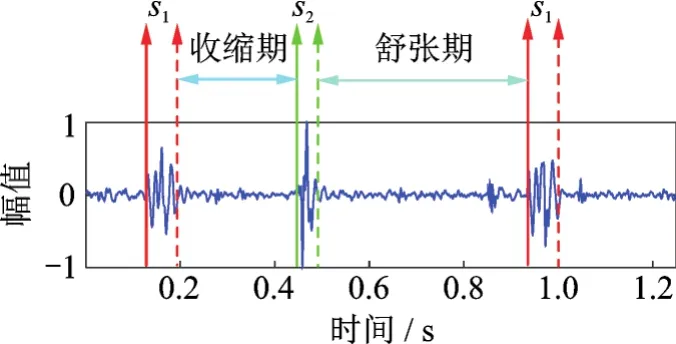
图2 心音成分Fig.2 Composition of heart sound

2 基于DHMM的心音分割

在心音信号的分割中，一些基于HMM的方法取得了显著的效果[7-9]。基于HMM的方法一般是通过大量人工标注的训练集提取特征参数，然后根据分割状态建立相应的模型，从而完成分割任务。

2.1 心音信号的标注

心音分割方法中，使用心电图与心音信号同步采集的方法，为心音分割提供了有效的参考，是目前精度最高的分割方法之一[2,12]。但在临床诊断中，该方法由于操作复杂，增加了医护人员的操作难度，临床应用可行性较差。同时，为了便于心音分析在常规体检项目中应用，对实时性的要求也较高。故该方法只在对精度有较高要求的情况下得到了一定的应用。

部分研究者提出通过参考心电信号标注训练集训练模型的方法来提高分割精度。然而，该方法在扩大更新标注训练集时耗时耗力，显然不可行。只通过采集心音信号标注的方法，虽然精度略低于参考心电信号的方法，但其临床实用性强，操作简单，得到了广大研究者和医护人员的认可，成为现阶段主要的研究方向。

2.2 面向心音信号的HMM与DHMM

HMM是一种关于时间序列的统计模型，它在满足马尔可夫性的基础上，描述了隐含的随机序列转移及生成对应的可观测随机序列的过程，是一类双离散随机序列[13]模型。一个简单的HMM过程的描述如图3所示。隐含状态随机序列转移过程描述的是有限个可知状态的随机转移过程，其转移状态序列是不可知的；可观测随机序列描述的是隐含状态与可观测序列间的一种关联统计关系，可观测序列是可知的[14]。HMM隐含序列转移到下一时刻的状态仅与隐含序列当前时刻的状态相关，而与观测随机序列和隐含序列过去时刻的状态无关。因此，HMM符合心音序列的统计模型，能够较好地描述心音序列的短时平稳性及整体的非平稳性。

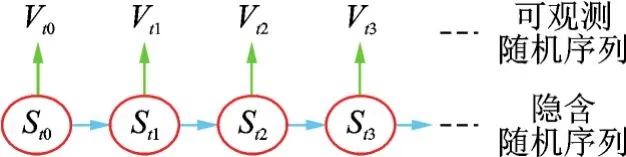
图3HMM过程Fig.3 The process of HMM

一个基本的HMM中的关键参数主要包括有限数目的隐含状态集合S及隐含状态序列St，各隐含状态所有的可观察值集合VOS及与隐含序列对应的观察序列Vt，各隐含状态的初始概率分布πc，各隐含状态间的转移概率矩阵δ，以及各隐含状态可能的观察值对应的概率分布矩阵Ψ。其中πc和δ决定了隐含状态序列，Ψ决定了观察值序列，因此往往将一个基本的HMM模型概括为

在利用HMM分割心音信号时，其有限状态集合可表示为

则其转移矩阵可表示如表1，其中ST表示跳转至本状态的概率，SN表示跳转至下一状态的概率，STi+SNi=1，STi＞SNi,1 ≤i≤ 4。

由于HMM的状态转移存在两种情况，即本状态至本状态或者本状态至下一状态，容易出现个别点误判现象，且转移状态数目较多，概率匹配相对复杂。因此考虑将HMM模型进行优化，以寻求更好的性能。考虑采用基于时间相关性的隐马尔可夫模型(Duration-dependent hidden Markov model,DHMM)[9]来对分割过程进行优化。

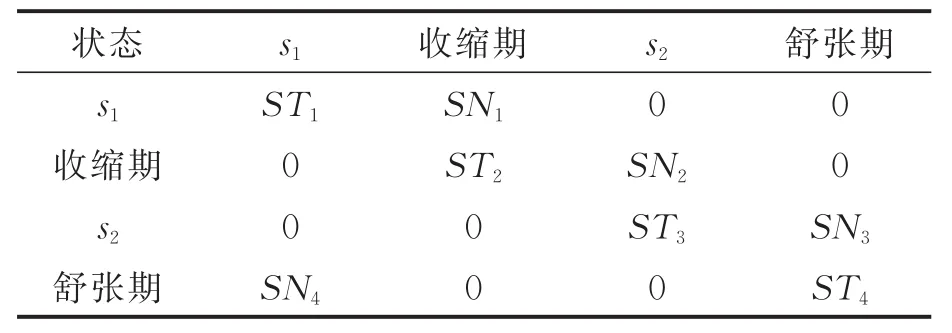
表1 心音的HMM状态转移矩阵Tab.1 HMM state transition matrix of heart sounds

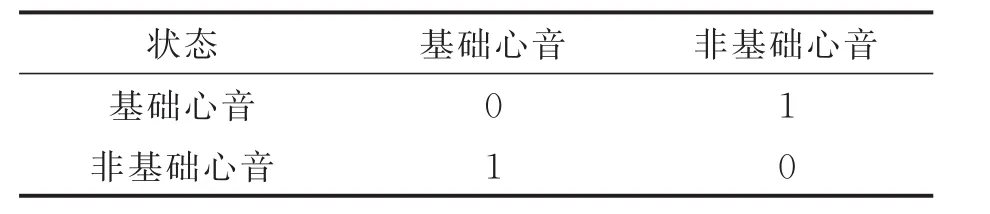
表2 心音的DHMM状态转移矩阵Tab.2 DHMM state transition matrix of heart sounds

DHMM与HMM的不同之处在于对状态转移加入了时间关系的条件限制，即经过一段相关联时间的累积，当各状态跳转时间的联合转移概率满足条件时才判断为状态转移，不满足则认为仍是当前状态[9]。同时，仅将转移状态划分为基础心音和非基础心音两类，无需划分为s1，收缩期，s2和舒张期4类，模型更加精简化。由于心音信号总是按照s1，收缩期，s2和舒张期的成分循环出现，且舒张期持续时长一般大于收缩期持续时长，故能较容易地在区分基础心音与非基础心音的基础上将4类成分区分开来。因此在DHMM下的有限状态集合可表示为

其状态转移矩阵可表示为表2。

在DHMM中，前向概率δt(j)[15]可表示为

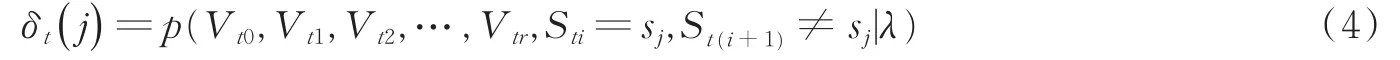
即i时刻隐含值Sti为j状态sj，i+1时刻隐含值St(i+1)不为sj，即发生跳转。则Sti为sj状态最后时间的概率可表示为

式中：pj(d)表示状态时长d下的分布概率密度函数[15-16]；δt-d(i)表示t-d为i状态下的最后时刻的概率；aij表示从i状态跳转至j状态的概率。则可将前向概率表示为

其中d和i的最大化值将用于后续的回溯算法，详细可参考文献[15,16]。

2.3 心动周期的提取

心音信号的各心动周期之间的差异较小，且医学上往往是在机体活动稳定的状态下在进行采集，以保证心率的变异性较低。在理想的环境下采集到的正常心音信号一般呈准周期特性，即各心动周期的持续时长基本一致。

心音信号具有短时平稳性，研究中普遍认为在10～30 ms内心音信号可视作平稳[5]。各心动周期变异性较低的情况下，通过自相关法能够较好地提取出心动周期的长度，自相关方法的特征包络提取可表达为

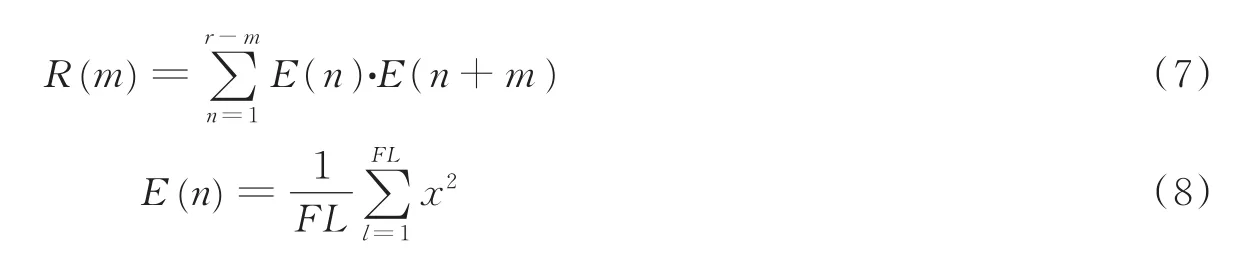
式中：E(n)为待分割的心音信号的第n帧信号短时平均能量，r为信号的总长度，FL为帧长。求取的自相关包络如图4所示。在图4中，每隔一段时间会出现一个峰值，每两个峰值间对应的时移恰好是一个心动周期持续时间的长度。在心动周期的提取中，可采用如下方法：

（1）采用中值滤波方法将包络进行平滑，去除每两个峰值点间存在干扰的极大值点；

（2）提取相关函数包络的极大值点；

（3）对提出的极大值点进行降序排列，取出前两个极值点的位置信息；

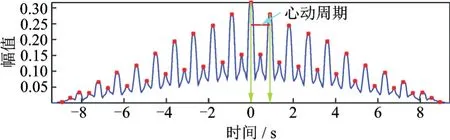
图4 自相关提取心音周期Fig.4 Autocorrelation extraction heart sound cycle

2.4EEMD分解

根据2.3节中提取的心动周期T，将心音信号划分为若干个心动周期，并对各心音周期进行集合经验模态分解（Ensemble empirical mode decomposition,EEMD）[17],得到多个本征模态函数（Intrinsic mode function,IMF）分量，每个IMF分量中都可能包含有用心音信号。这里采用IMF分量与心音信号的相关系数差值来衡量心音成分含量的多少，剔除部分无用的IMF分量，在抑制噪声的同时以尽量多的含心音信号的IMF分量重构来表征心音信号，其可分析性更高。相关系数的定义如下

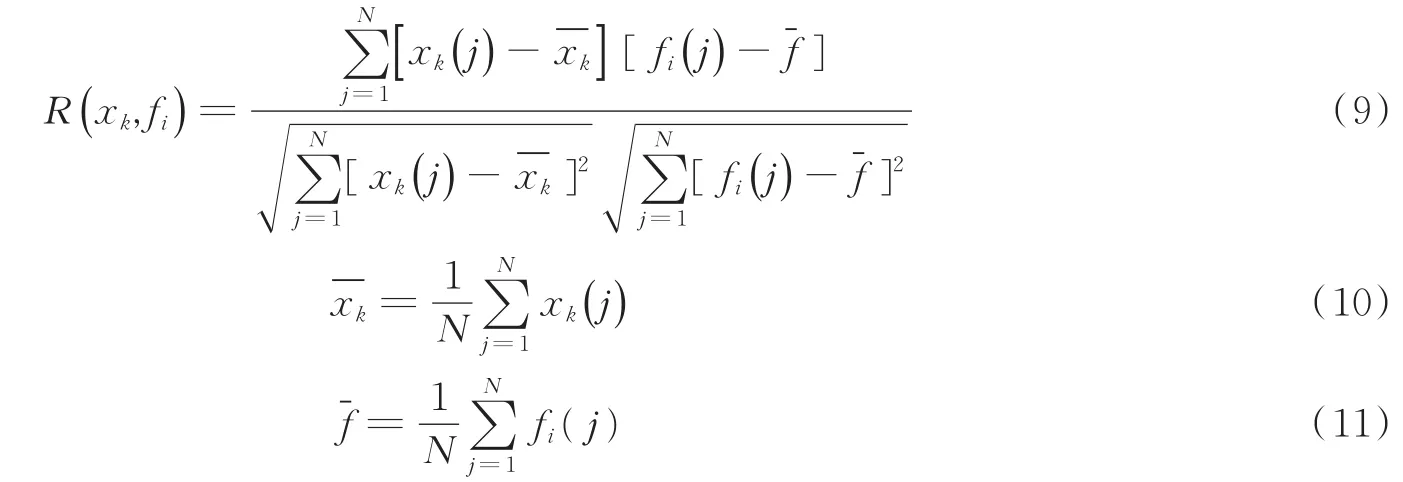
式中：N为分量总数，xk表示第k个心动周期为第k个心动周期的均值；fi表示第i个IMF分量表示各IMF分量的均值。相关系数差值可表示为

在相关系数的判决中，求得的互相关系数差值ΔRki的第一个局部最小值fk，则fk+1可视作模态混叠分量。这里将前k个IMF分量视为噪声分量，其中心有效的音信号分量极少，因此可直接丢弃，将剩余分量进行重构即得到各心动周期的模态本征信号。

2.5 心音信号的高斯建模

基础心音和非基础心音存在某种约束关系[18-19]，本文分析了心动周期内的短时平均能量分布及其直方分布，建立如图5所示的高斯混合模型（Gaussian mixture model,GMM）。

图5（a）为一心动周期内短时平均能量分布图，图5（b）为噪声干扰下的心音信号时域波形图，与图5(a)相对应；图5(c)为根据短时能量分布特征进行的高斯拟合过程。由于非基础心音信号持续时间较长，出现次数较多，且短时平均能量较小，集中在0附近，故拟合的高斯波形狭窄而高，即高斯模型方差较小；基础心音信号持续时间较短，总的出现次数较小，短时平均能量分布较为分散，故拟合的高斯波形宽广而矮，即方差较大。4类常见噪声的干扰均符合上述情况，因此可根据直方分布情况建立GMM模型，即式中：σn为标准差，ηn为期望值，n=1或2。当n=1时，表示为非基础心音；当n=2时，表示为基础心音。

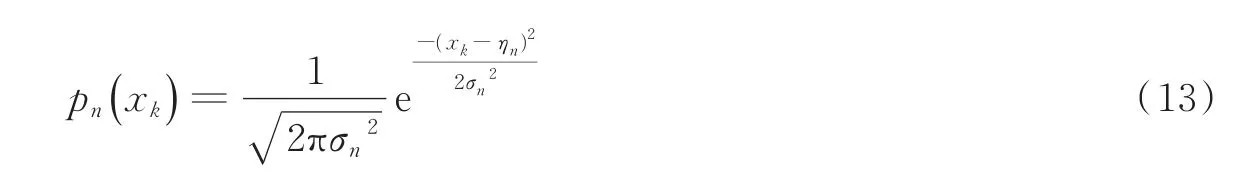
图5 心动周期的高斯建模Fig.5 Gaussian modeling of cardiac cycle

模型的约束关系可概括为[18]：

前瞻性研究。本研究数据分析采用SPSS 22.0软件包，采用重复测量的方差分析、卡方检验进行数据比较。以P＜0.05为差异有统计学意义。

（1） 基础心音和非基础心音状态间的约束关系为式中：τ＞0，用于防止误判和基础心音泄漏，其估计为

式中ρ为常数。

（2） 方差间的约束关系为

非基础心音段将基础心音方差设置为σ1，通过约束条件（1，2）使得模型区分两种状态的能力得以保持。

通过约束关系建立合适的GMM模型，由DHMM模型训练，来完成基础心音与非基础心音的判别，此时模型可表示为

3 心音信号的分割流程

本算法是基于准周期心音信号前提提出的，分割处理的心音信号心率变异性应较小。整个心音分割流程可概括为以下6个步骤，流程图如图6所示。

（1）输入待分割的心音信号并作预处理，通过自相关包络获取心动周期均值T；

（2）通过EEMD分解计算每个心动周期的IMF分量，计算相关系数R(xk,fi)并用其差值ΔRki第1个极小值后的分量重构信号；

（3）通过约束关系训练出适用于区分基础心音和非基础心音的GMM模型，求得期望ηn及方差σn；

（4）计算DHMM的初始概率分布πc，状态转移概率矩阵δ，以及各状态可能的观察值对应的概率分布矩阵Ψ，结合GMM模型，生成分割模型λ={πc,δ,Ψ,ηn,σn}；

（5）对状态跳转的判断及修正，得到基础心音及非基础心音的区分结果；

（6）通过心音信号的时域特征识别出收缩期及舒张期，区分出s1，收缩期，s2和舒张期，得到心动周期内的分割结果。

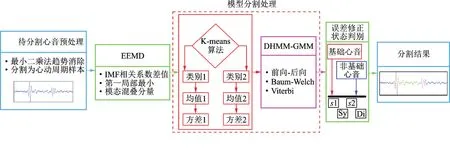
图6 心音分割算法流程图Fig.6 Flow chart of heart sound segmentation algorithm

4 实验结果及分析

实验选用的低心率变异性数据来源于中国医学科学院阜外医院采集提供和“PhysioNet/Computing in Cardiology Challenge 2016”的数据集，并在心内科从业人员的指导下对多组实验数据进行了人工标记。实验所用心音频率为2 kHz,均为心率变异率较低的心音。在心率变异性较低的情况下，选用了4类干扰噪声：脉冲噪声、Babble类语音噪声、白噪声和粉红噪声。实验中所用脉冲噪声采样率为1 kHz，Babble类语音噪声及白噪声采样率为1.6 kHz，粉红采样率为44.1 kHz，并对4类噪声作变采样（上采样或者降采样）处理变为2 kHz；帧长为20 ms，帧移为10 ms,窗函数为hamming窗,所有心音均已采用最小二乘法拟合进行趋势项消除处理。实验所用电脑CPU型号为Intel(R)Core(TM)i78700kCPU-@3.70 GHz，RAM为16.0 GB，硬盘为1 T，仿真软件为MATLAB2017a。为了检验分割算法的有效性及可靠性，验证了4类噪声在不同信噪比下对算法分割精度的干扰，并与基于逻辑回归的隐半马尔可夫模型(Logistic regression hidden semi-Markov model,LRHSMM)的算法[8]和基于Hilbert的算法[4]进行了对比。

实验中，共处理238条样本信号，约8 000个心动周期。由于部分心音信号并不是太理想，故采用了4个评价指标[20]对算法进行评价：算法处理耗时（PS）、基础心音检出正确率（TPS12）、基础心音错误检入率（FPS12）和基础心音未检出率（MPS12）。计算方法为

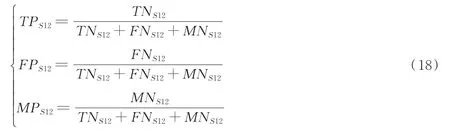
式中：TNS12为基础心音正确检出帧数，FNS12为基础心音错误检入帧数，MNS12为基础心音未检出帧数。计算中，以人工标注的数据为参考标准。

表3中给出了测试白噪声干扰，SNR分别为15，10，5和0 dB下3种算法的基础心音检出正确率，图7中给出了不同信噪比4类噪声下的检出正确率。

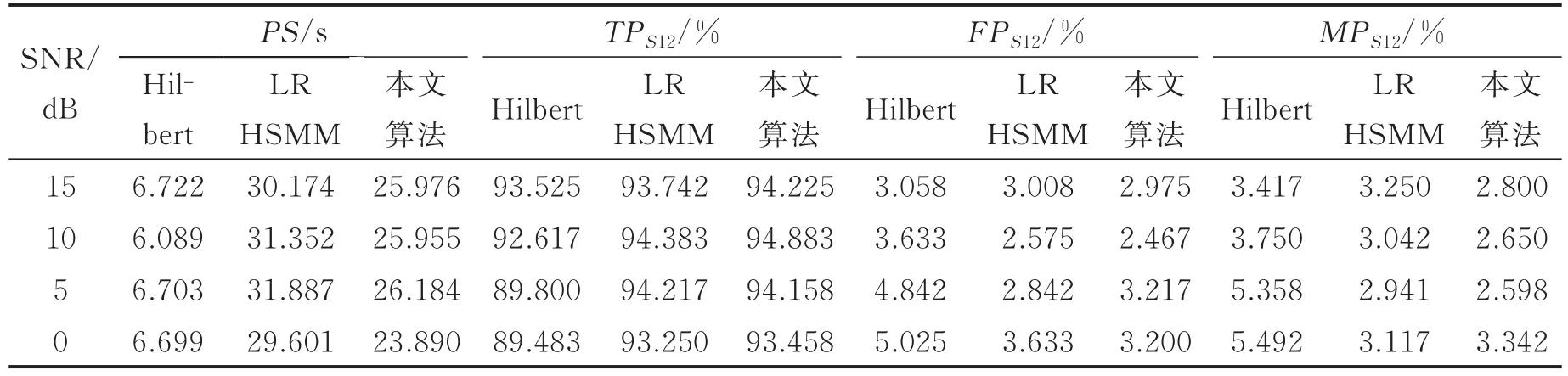
表3 白噪声下的评价指标对比Tab.3 Comparison of evaluation indicators under white noise

图7 不同信噪比4类噪声干扰下的检出正确率Fig.7 Detection accuracy rate under four types of noise interference with different SNRs

图7中反映出，Hilbert算法在信噪比较高的情况下检出正确率较高，可达92%以上，具有较好的分割性能，但随信噪比降低，其检出正确率也明显下降,且波动较大，抗噪性能相对较弱。在信噪比较高时，LRHSMM算法检出正确率可达94%左右，略高于Hilbert方法检出正确率，但随信噪比降低LRHSMM算法的检出正确率明显高于Hilbert方法，且检出正确率波动较小，抗噪性能较好。本文提出的DHMM方法检出正确率可达94%以上，略高于LRHSMM方法。这是由于本文算法在低心率变异下通过GMM模型进行约束能更好地匹配心音信号特征，降低了泛化效果对分割精度的干扰，且不受受试者间心动周期差异的影响。

在PS指标中，取平均作为PS评价值。Hilbert方法每条心音检出耗时在6.7 s左右，耗时短，实时性好，但复杂声学环境下分割精度相对较低；LRHSMM方法每条心音检出耗时在30 s左右，运算时间明显高于Hilbert算法，但其分割精度也高于Hilbert算法；本文DHMM方法每条心音检出耗时在25 s左右，运算时长较LRHSMM短，且LRHSMM方法通过大量训练集进行训练，耗时耗力，而本文算法采用在线训练方法更为简便，其分割精度也较高。

图8给出了原始心动周期与4类噪声干扰下的心动周期在DHMM中分割结果的对比。从图8（ad）分割结果与原始心动周期分割结果可以直观地看出，本文算法在各类噪声干扰下依然具备良好的分割性能。

5 结束语

在心率变异性较低的心音信号分割中，DHMM较好地结合了心音信号的准周期性、短时平稳性及其主要成分在时域下的分布特点。DHMM简化了HMM中的状态转移过程，由s1，收缩期，s2和舒张期间的转换直接变为基础心音及非基础心音间的转换。通过自相关函数可较准确地提取出心音周期，采用EEMD提取模态本征信号表征心音信号，分析心音短时平均能量分布直方图可建立GMM模型以区分基础心音和非基础心音，当基础心音的判断满足关联时间要求时方可发生状态跳转。该过程较好地描述了心音信号的状态转移过程，且在低心率变异情况下，本文提出的方法能更好地匹配心音信号特征，较LRHSMM及Hilbert方法更适用于心率变异性较低的心音定位分割。后续工作可对如何提高算法对心音变异容忍度进行研究，以提高算法的适应能力，扩大算法的适用范围。

图8 SNR=10 dB时4类噪声干扰下的分割效果Fig.8 Segmentation effect under four types of noise interference with SNR=10 dB