数学探究课堂的实践与思考

☉江苏省通州高级中学 姚振飞

生命的河流往往会不分昼夜地奔向它理想的海洋，困难与挫折在它奔向海洋的过程中难免存在，就好比人的一生，不过，心存伟大理想的我们一定能够克服困难与挫折并满怀喜悦地直奔前方.如何正确引导青少年树立远大的理想是每个教师都应思考的问题，担负着“传道、授业、解惑”伟大职责的我们应在课堂教学中融入更多的人生哲理，帮助青少年学生在“现在学习，将来圆梦”的正确引导中展开学习并树立人生理想.因此，我们应该引导学生走进开放、探究的课堂并在内驱力的促动下直奔前方.

孔子有云：“疑，思之始，学之竭”.问题的提出能使学生的学习兴趣得到诱发并使其在阅读与思考中获得更加深刻的理解，使学生在自身理解与知识、经验的结合之下顺利构建有关数学问题，增强学生学数学、用数学的意识的同时促发其主动探究的意识.学生在自主探索获得答案之后往往会建立与数学之间的亲近感，充分感受学数学、用数学的实践和体验并逐步树立起学好数学的自信心，这对于其实现远大理想目标来说是极其有意义的.

一、实践中体验成功

事实上，学生与生俱来就具备一定的探究性学习的能力，只不过需要教师适时的点拨与启发.学生在现实的数学活动中对数学知识、思想、方法形成理解与掌握需要教师的有益设计与引导，但这并不意味着教师的单纯讲解能够起到多大的作用，这需要教师的精心设计与启发并使学生在自主探究与合作交流中展开真正意义上的探究性学习.“做数学”是新课程理念中尤为值得关注的重大思想，这其实是对学生亲身经历数学、探究数学、体验数学的重视和提倡.教材中的很多例题与习题蕴含着一些重要的数学思想方法与探究理念，教师若能对这些资源进行巧妙的设计与充分的利用，一定能将数学课堂建设成为适合学生展开探究性学习的舞台.

例1已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB=1，BC=2，过点A作AE⊥CD，垂足记作E，现将△ADE沿AE折叠，使DE⊥EC.试在线段AE上找一点R，使面BDR⊥面DCB，并说明理由.

图1

请高三即将参加高考的学生直接给出这一问题的答案是有一定难度的，但给予学生一定的时间进行思考，很多学生都表现得跃跃欲试.

生1：设AR=x，过点R作RK⊥DB，垂足为K，过点K作FK⊥BC，垂足为F，连结RF，则KF=FB=x，，在Rt△DKR中，根据勾股定理可得，因此R是AE上靠近A的一个四等分点.

师：这样做的理由是什么呢？

生1：我们经常会运用数量来衡量并确定点的位置，因此我就想到建立数量关系并进行求解了.

师：这种解法将解决问题的目标意识很好地体现了出来，树立解题目标之后，坚定地走下去就能实现目标.我们的青少年也要像解决此题一样，树立远大理想并坚定信心地走下去.

生2：分析已知条件可以知道，点R满足3AR=RE时，面BDR⊥面BDC.

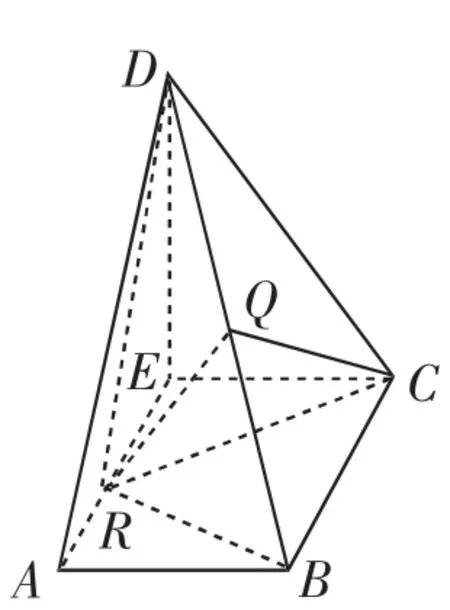
图2

证明：如图2，取BD的中点Q，连结DR、BR、CR、CQ、RQ.

又在△CBD中，CD=CB，Q为BD的中点，所以CQ⊥BD.所以CQ⊥面BDR.所以面BDC⊥面BDR.

生3：过点C作CM⊥DB，垂足为M，过点M作MN⊥BE，垂足为N，连结CN，则CN⊥BR，则易得R为AE上靠近点A的一个四等分点.

生4：过点E作ES⊥CD，垂足为S，过点S作SQ∥BC，交BD于点Q，取ER=SQ，连结RQ，容易得出R为AE上靠近A的一个四等分点.

师：通过大家的共同努力和探究，我们发现了结论，也收获了成功，由此可见，理想的实现是需要努力的，大家肯定在今天的学习中又一次理解了这一道理.

二、拓展中培养自信

在类比、引申、推广中对问题进行拓展以及新的探究，能使学生在更深层次的探究中获得基础知识的巩固，使学生的探索精神与创新能力得到锻炼与发展并由此建立学习自信.比如以下一道习题.

笔者在此题获得证明之后又进行了如下问题的设计与提出：如果将（2）中的条件进行适当的改变并对新问题的结论进行探求，是否可以将这一命题进行推广呢？大家谈谈自己的思考.提出问题并给予学生充裕的时间进行思考，鼓励学生对（2）中的条件进行自主思考与变更，对新问题的结论进行自主探索或推广，最后请学生将自己的探究成果进行展示和解说.

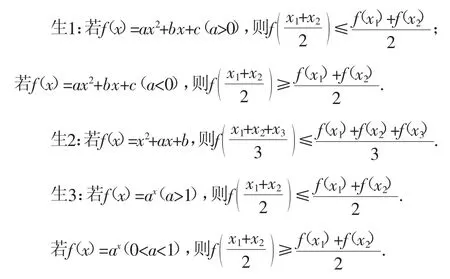
师：大家勇于探索、敢于创新的精神令老师刮目相看，表现非常棒，老师相信大家在各自的成长道路上也一定会表现得越来越精彩.大家在自主探索和集体讨论中对所得结论进行了新的推证并达成共识，这对大家来说是难能可贵的经历.不过大家的讨论有的对，有的错，生1、生2、生5的证明是对的，生3、生4则错了，大家能帮助这两位同学进行修正吗？

生6：生3的结论可以修改成：若f（x）=ax（a＞0且a≠1）都有

生7：生4的结论可以修改成：若f（x）=logax（a＞0且a≠1），对任意x1、x2∈（0，+∞），当a＞1时，有当0＜a＜1时，有

师：非常棒，那么我们在指数函数与对数函数的结论的比较上是否能够得到什么启发呢？大家能否抓住这一讨论的契机进行规律的探寻和总结呢？

学生在一系列的探究与教师的启发下得出以下凸函数的性质：如果定义在区间I上的函数y=f（x）为下凸函数，那么对任意x1、x2∈I，则有如果定义在区间I上的函数y=f（x）为上凸函数，那么对任意x1、x2∈I，则有

由此可见，理论联系实践的探究对于学生来说具有积极的意义，教师在实际教学中不能单纯注重学生的模仿与记忆，而应创设出适合学生动手操作、自主探索与合作交流的平台并以此促进学生的自主探究与学习，鼓励学生结合自身的经验、认知规律进行数学问题的探索与解决，使学生在观察、探索、讨论与研究中不断积累丰富的感性认识，在不断经历的实践感受中获得认知、理解、辨析、解题、创造能力的长足发展.