对一道模拟题的多解探究
2019-09-06江苏省丹阳高级中学张栋斌
☉江苏省丹阳高级中学 张栋斌
三角形中的最值问题是解三角形问题中的重点与难点之一,也是新课标大纲充分体现在“知识点交汇处”命题的一大阵地.通过活泼多样的问题背景设置,题目形象直观,条件中知识交汇点众多,题目具有相当的难度,同时解决问题的思维方式多变,破解方法也多种多样,一直是历年高考、竞赛命题中的基本考点和热点之一.
【例】(2019届江苏省无锡市高三上学期期末检测·14)在锐角三角形ABC中,已知2sin2A+sin2B=2sin2C,则的最小值为______.
本题以锐角三角形ABC为问题背景,通过已知三角关系式2sin2A+sin2B=2sin2C,进而求解三角形的三内角的正切值倒数之和的最小值问题.题中涉及角的参数较多,且三内角之间又相互关联,可以通过题目条件的转化,再借助基本的数学工具(二次函数、三角函数、基本不等式、导数等)来破解相应的最小值问题.
结合题目中的三角关系式,从三角恒等变换的角度或从正弦定理与余弦定理的角度转化,利用相关的三角形内角和公式、诱导公式、同角三角函数基本关系式以及三角恒等变换公式的应用得到3tanA=tanC,再利用两角和的正切公式得到tanB关于tanA的表达式,从而把三角式转化为关于tanA的表达式,最后利用基本不等式即可确定对应的最值问题.
解法1:由2sin2A+sin2B=2sin2C,变形2sin2A-2sin2C=-sin2B,
可得2sin(A+C)sin(A-C)=-sin2B,
即有2sin(A-C)=-sinB,
那么2sinAcosC-2cosAsinC=-sinB=-sin(A+C)=-sinAcosC-cosAsinC,
即3sinAcosC=cosAsinC,亦即3tanA=tanC.


解法2:由2sin2A+sin2B=2sin2C,结合正弦定理可得2a2+b2=2c2,则有b2=2c2-2a2,
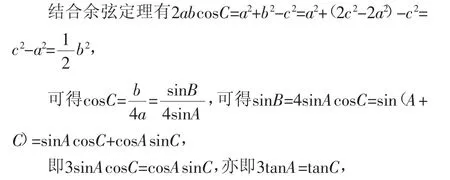
以下同解法1.
通过三角恒等变换的角度或从正弦定理与余弦定理的角度得到3tanA=tanC,利用斜三角形中的三角恒等式tanA+tanB+tanC=tanAtanBtanC,借助参数的引入加以转化,并利用基本不等式或导数法即可确定相应的最值问题.
解法3:由解法1或解法2可得3tanA=tanC,
设tanA=x,tanB=y,tanC=z,
结合斜三角形中的三角恒等式tanA+tanB+tanC=tanAtanBtanC,可得x+y+z=xyz,
又z=3x,代入整理要得4x+y=3x2y,即

解法4:由解法3可得,
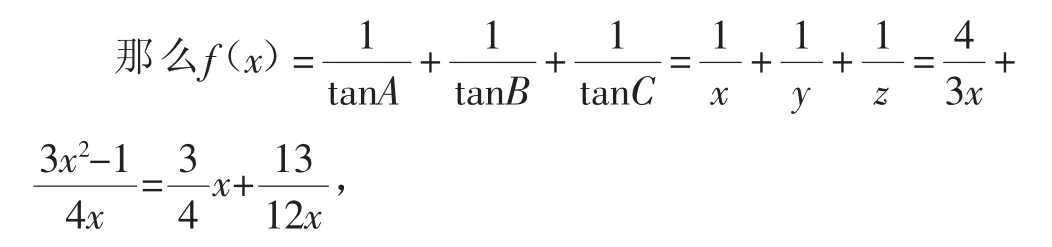

结合题目中的三角关系式,先利用正弦定理得到b2=2c2-2a2,通过平面几何作图,过点B作BD⊥AC于点D,引入参数x,y,h,利用三角函数的定义分别可以确定tanA与tanC的表达式,或借助余弦定理的转化并结合条件确定参数x,y之间的关系,再利用两角和的正切公式得到tanB的相关表达式,从而把三角式转化为关于参数h与y的表达式,再利用基本不等式即可确定对应的最值问题.
解法5:由2sin2A+sin2B=2sin2C,结合正弦定理可得2a2+b2=2c2,则有b2=2c2-2a2,
如图1,过点B作BD⊥AC于点D,
设AD=x,CD=y,BD=h,
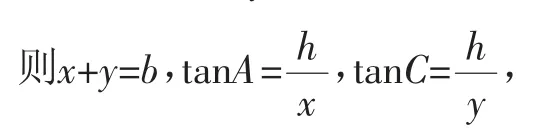

图1
而(x+y)2=b2=2c2-2a2=2(x2+h2)-2(y2+h2)=2(x2-y2),整理可得x=3y,


解法6:由2sin2A+sin2B=2sin2C,结合正弦定理可得2a2+b2=2c2,则有b2=2c2-2a2,
如图1,过点B作BD⊥AC于点D,
设AD=x,CD=y,BD=h,

以下同解法5.
结合题目中的三角关系式,先利用正弦定理得到2a2+b2=2c2,再通过余弦定理的转化得到,利用对三角式的三角恒等转化得到其值为,把问题转化为求解三角函数关系式的最值问题,然后可以借助导数法等来破解.
规律总结
破解三角形中的最值问题,可以通过三角函数的角度或平面几何的角度来切入,无论借助哪种思路来进行破解,往往都综合基本不等式求最值、三角函数求最值、数形结合求最值等方法与技巧来处理,充分体现了知识与方法的多样性与全面化.
其实,对于解三角形问题与三角函数的有机巧妙融合问题,往往可以综合提升不同的知识点间的整合与能力的拓展.同时,此类问题大都运算量较大、公式应用较多,要求我们不仅具有较高的运算水平、较强的运算能力和较好的记忆能力,还应该善于审题,采用相应的破解策略,全面优化过程,提升解题效益,培养数学素养.
