基于GA-BP的渗透系数多目标反演分析模型研究*

高培培，章 光，胡少华,2，武晓炜，文 锋，刘 志

(1.武汉理工大学 安全科学与应急管理学院，湖北 武汉 430070；2.武汉理工大学 道路桥梁与结构工程湖北省重点实验室，湖北 武汉 430070)

0 引言

为开发利用河流水利资源，减少洪涝灾害，我国兴建了大量的水库大坝等基础设施。由于大坝长期处于高压水环境中，水在坝体内形成渗流，渗流场通过施加渗流作用力影响着应力场，同时应力场又反过来改变了坝体的渗透系数。而渗透系数是大坝渗流计算分析与控制中重要的参数，是安全运行的重要物性指标[1]。确定准确、合理的渗透系数对于大坝的运行具有重要的意义。

传统岩体渗透系数获取方式主要是压水试验，由于受到工程扰动和时间效应的影响，大坝实际运行情况下的岩体渗流参数已经发生了改变，压水试验所获得的渗透系数存在一定的误差[2-3]。而根据工程监测数据反演的方法以其经济、快速的特点，成为了确定渗透系数的一种重要的途径。由于大坝渗流具有非线性特点，在渗流系数反演的目标函数中具有多值问题，传统的线性参数反演已经无法解决其阈值优化问题[4-6]。随着人工智能的高速发展，BP神经网络以其简单的结构、良好的自学能力、有效解决非线性目标函数的逼近问题等优点，越来越多地被应用于渗透系数反演问题。如黄珊等[7]基于BP神经网络反演了大坝各区域的渗透系数，并结合模拟计算水头验证了反演结果的可靠性；Lingireddy等[8]基于人工神经网络，建立了一种渗流场含水层参数识别方法。然而，BP神经网络存在训练过程中会陷入局部最优的问题，反演精度下降，部分学者采用改进的算法来优化BP神经网络，如李守巨等[9]基于Levenberg-Marquardt算法优化的BP神经网络，开展了白山水电站基岩和防渗帷幕渗透系数反演研究；魏进兵等[10]根据现场的监测资料，采用遗传算法对泄滩滑坡各地层渗透系数进行了反演分析，结果真实可靠。

另一方面，在渗透系数反演过程中，部分学者仅采用实测水头或渗流量来反演，如王媛等[11]采用水头实测资料，通过混合遗传算法反演坝基材料的相对渗透系数，反演结果不唯一。研究表明[12]，大坝渗流区域内某一位置的扬压力仅仅与大坝各介质的相对渗透系数有关，渗流量与大坝各介质的绝对渗透系数有关。故真实渗透系数的反演应充分结合实测渗流量与水头场分布进行。

综上所述，针对渗透系数反演问题，国内外学者已开展了大量研究。本文通过对渗流反演问题进行分析，以水口大坝为研究对象，建立了渗透系数多目标反演模型，开展了水口大坝坝体、坝基和防渗帷幕渗透系数反演研究，并对反演结果进行了验证。

1 渗透系数反演分析

1.1 问题描述

大坝的渗流问题为典型的无压渗流场，属边界非线性问题。当渗控效应评价以长期稳定运行为主要目标时，可将其简化为稳定渗流问题。根据质量守恒定理，各向同性介质三维渗流控制方程为[13]：

(1)

式中：k为渗透系数，m/s；h为水头。

开展渗流分析的主要目的是通过数值模拟求取渗流场中水头、流量等渗流要素时空分布特征，但数值模拟的前提是得到真实可靠的渗透系数。由渗流控制方程可知，渗透系数k放大或缩小若干倍数，渗流场内的水头分布不受任何影响，渗透系数不能通过压力水头的监测数据唯一确定，因此需要引入渗流量作为目标函数进行反演。通过某一断面S的渗流量Q可表示为[14]：

(2)

式中：k为渗透系数，m/s；qn为断面S表面的单位渗流量，L/(s·m)；n为断面S上的结点总数；i,j为断面S上结点编号。

以水头、流量等实测数据为已知信息，通过采用合理的反演分析方法，逆推渗流场中各介质的渗透系数，可以解决渗透系数反演唯一性的问题。

1.2 渗透系数反演模型

本文在渗透系数反演分析时采用正交设计、有限元正分析和GA-BP神经网络相结合的反演分析方法。其中，正交设计用于安排有限元正分析所需的参数方案，以减少正分析的次数，提高反演效率[15-16]；有限元正分析是在正交设计的参数方案的基础上进行模拟，计算出各水平渗透系数对应的扬压力和渗流量，从而生成神经网络的训练样本[17]；BP神经网络通过训练样本建立渗透系数和效应量之间的非线性映射关系，通过输入效应量实测数据反演渗透系数；BP神经网络在误差反向传播时有可能会得到局部最优权值，因此引入遗传算法来优化BP神经网络的权值和阈值以寻求最优反演参数[18-20]。GA-BP反演模型原理如图1所示。

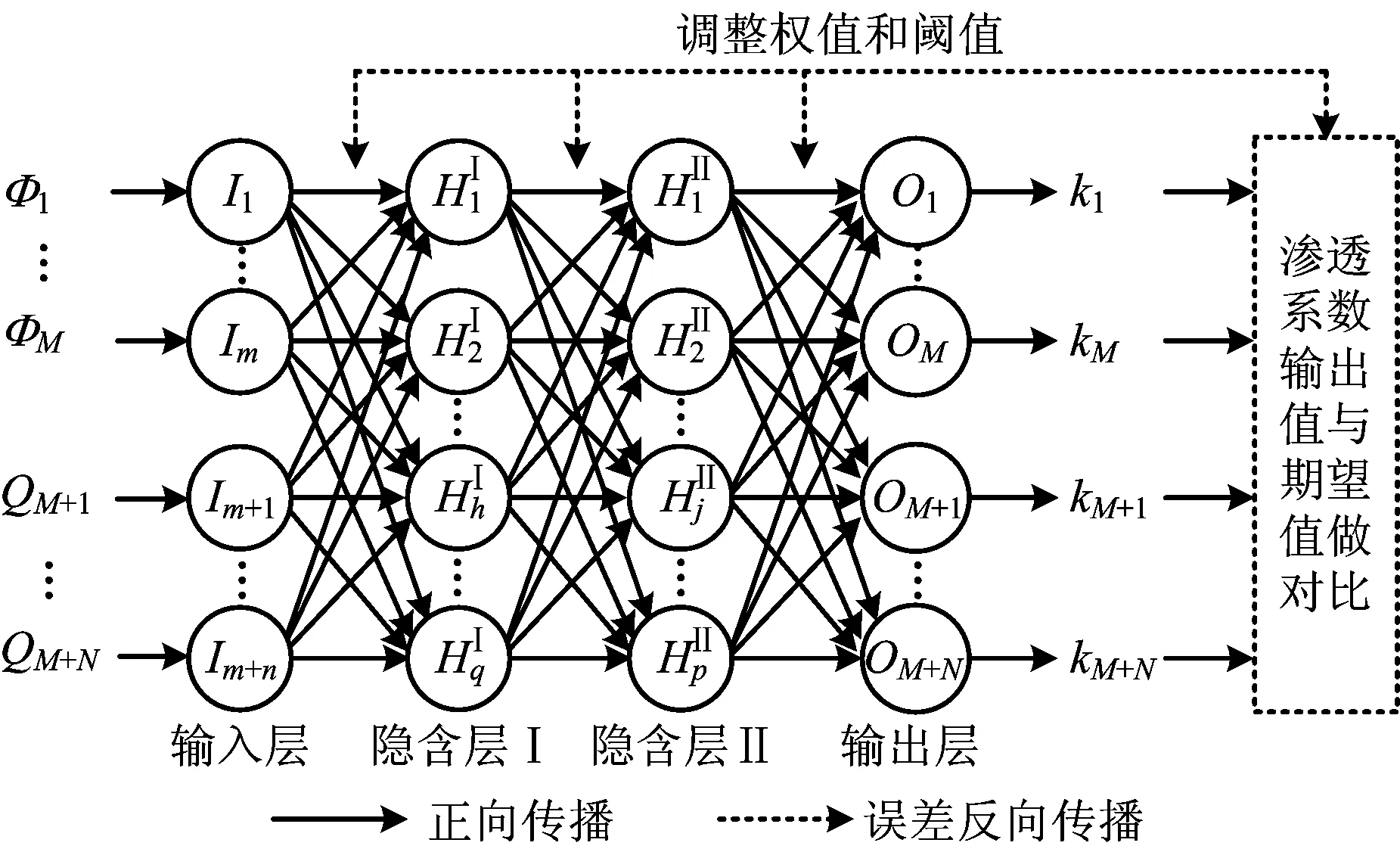
图1 GA-BP神经网络结构(双隐含层)Fig.1 Structure of GA-BP neural network (double hidden layers)

在渗透系数反演的过程中，假设待反演渗透系数有m个，用向量k表示，即k=[k1，k2，…，km]T；扬压力测点有M个，其中第i扬压力测点的实测数据为Φi(i=1，2，…，M)；渗流量测点为N个，其中第j渗流量测点的实测数据为Qj(j=1，2，…，N)。渗流反分析问题的数学表述为：在各待反演渗透系数的取值范围内，寻找一组最佳的渗透系数组合k，满足klow≤k≤kup(klow和kup分别为各渗透系数取值范围内的最大值和最小值，该值可根据大坝水文地质特征和压水试验估算而定)，并使得如下目标函数取最小值[21-23]：

(3)

式中：‖·‖2为向量的2-范数；w为权重系数；Φi(k)和Qj(k)为第i扬压力测点所计算的扬压力和第j渗流量测点所计算的渗流量。

同时，针对BP神经网络中神经元之间Sigmoid传递函数的输出恒大于0的问题，本文算法采用Tanh传递函数，与Sigmoid不同的是，Tanh函数输出值是0均值，该传递函数为：

f(x)=(ex-e-x)/(ex+e-x)

(4)

由于Tanh函数为渐进函数，输出区间为(-1，1)，如果将扬压力和渗流量直接输入神经网络会造成训练混乱，因此在进行大坝渗透系数反演时，在输入神经网络前需要将各介质渗透系数和扬压力、渗流量统一归一化到(-1，1)区间。同时，神经网络输出渗透系数为归一化值，反归一化后可获得渗透系数反演值。

1.3 渗透系数反演流程

本文建立的渗透系数反演模型，其具体实现流程如下：

1)针对坝段的实际情况，选取某坝段进行分析，建立三维渗流有限元模型，为确保计算结果的准确性，坝体排水廊道、灌浆廊道、排水孔和防渗帷幕均按照实际工况建模。

2)在待反演渗透系数的取值范围内(klow≤k≤kup)，采用正交设计方法选取若干个水平，设计出相应的渗透系数组合方案，将其代入有限元模型进行模拟，获得GA-BP神经网络训练样本。

3)以训练样本中测点扬压力和渗流量为神经网络的输入层单元，坝体各个岩石介质的渗透系数为输出层单元代入神经网络进行训练，以目标函数取最小值为目标，确定两类渗流效应量和渗透系数之间的非线性关系。

4)通过渗流效应量实测数据可靠性分析，选取某一时期的扬压力和渗流量的实测数据代入训练好的神经网络，获得实际工况下的渗透系数并进行验证。

渗流反演分析流程如图2所示。

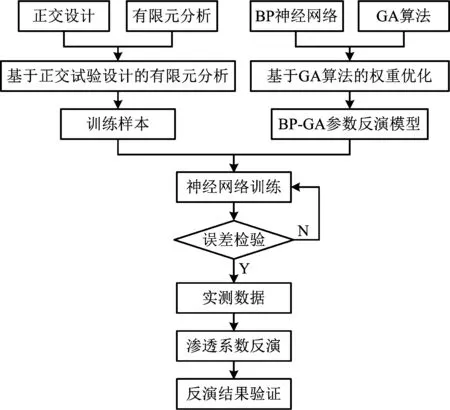
图2 渗流反演分析流程Fig.2 Procedure of seepage inversion analysis

2 工程验证

2.1 工程概况

水口大坝坝前正常蓄水位65.00 m，校核洪水位67.68 m，死水位55.00 m。坝址岩体为中生代燕山期呈岩株状侵入的黑云母花岗岩，岩性单一且致密坚硬完整。岩脉与黑云母花岗岩接触紧密，胶结良好。根据地质勘探资料，坝址区未发现较大的断层，仅见小断层及挤压破碎带，倾角陡，对工程影响较小。通过对坝基岩体进行简化，将基岩分为强风化花岗岩(埋深20 m)、弱风化花岗岩(埋深30 m)和新鲜基岩。新鲜基岩岩体透水性极弱，故反演过程主要考虑强风化花岗岩和弱风化花岗岩。

根据大坝实际工况，对引水坝段进行分析，并以x轴顺河指向下游为正，z轴为实际高程进行建模。计算范围分别为：坝体上游40 m，下游取40 m，深度取50 m，坝高74 m。模型采用Solid45单元进行网格映射划分，共划分单元99 686个，节点110 993个，如图3所示。

图3 引水坝段三维有限元模型Fig.3 Three-dimensional finite element model of diversion dam section

本次渗透系数反演研究采用引水坝段UP9，UP10，UP12扬压力以及WE3量水堰渗流量的实测数据，其扬压力时程曲线如图4所示，渗流量时程曲线如图5所示。

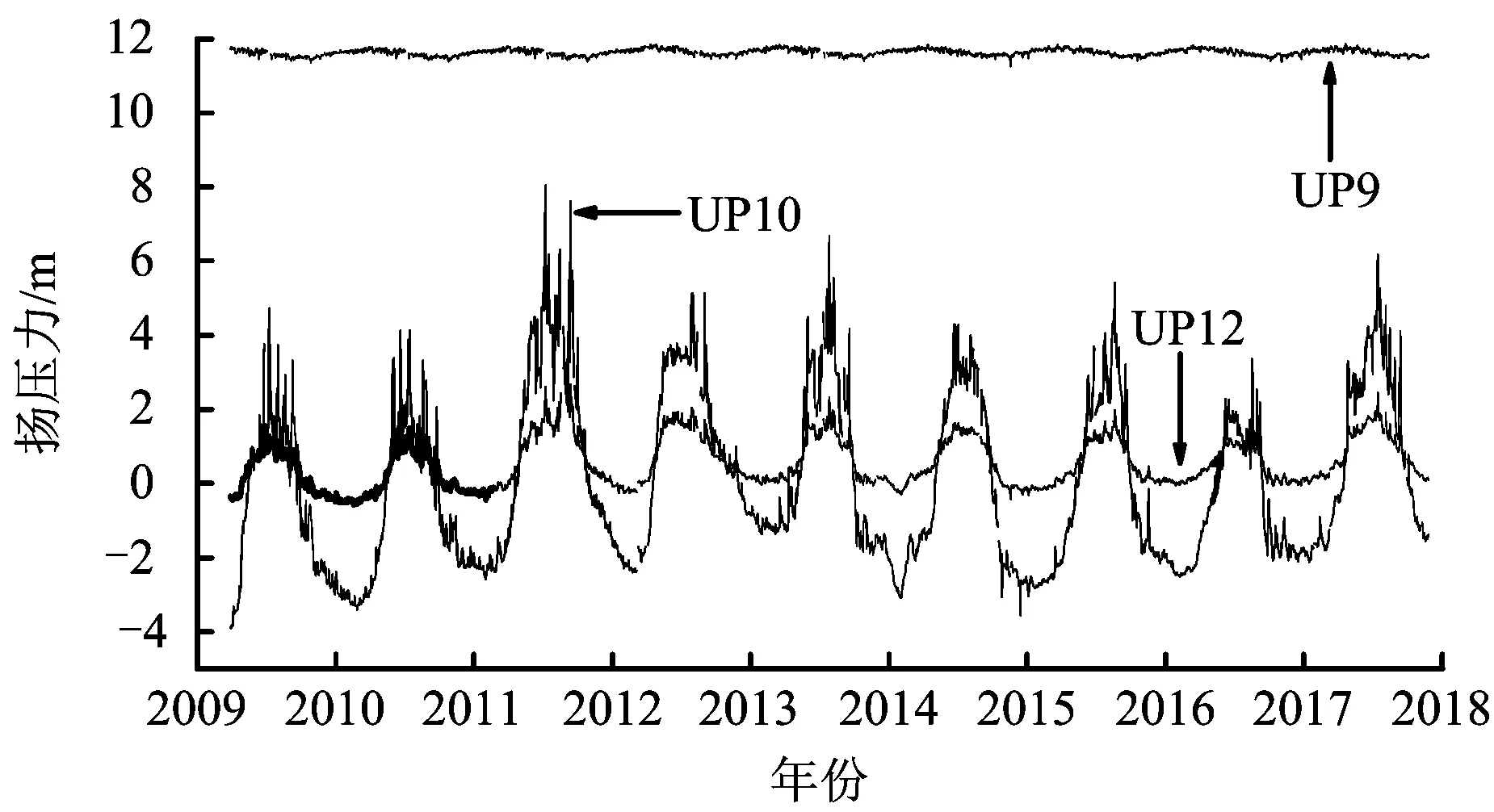
图4 2009-2018年扬压力实测数据Fig.4 Measured data of uplift pressure in 2009-2018

图5 2009-2018年渗流量实测数据Fig.5 Measured data of seepage quantity in 2009-2018

2.2 计算过程

在坝址区对各个岩石介质进行取样并进行压水试验，同时根据工程经验，确定水口大坝各介质渗透系数取值范围，见表1。

表1 渗透系数取值范围及反演结果Table 1 Values range and inversion results of permeability coefficient m/s

鉴于训练样本数量对反演精度的影响，大坝各介质渗透系数取7个水平，各水平取值见表2。将正交设计安排的待反演参数代入引水坝段有限元模型中进行计算。

BP神经网络隐含层层数和神经元个数对预测结果有重要影响，通过试算，采用4-9-34-4的神经网络结构时，预测结果误差最小。使用遗传算法对BP神经网络进行优化时，种群规模设置为100，交叉概率为0.9，

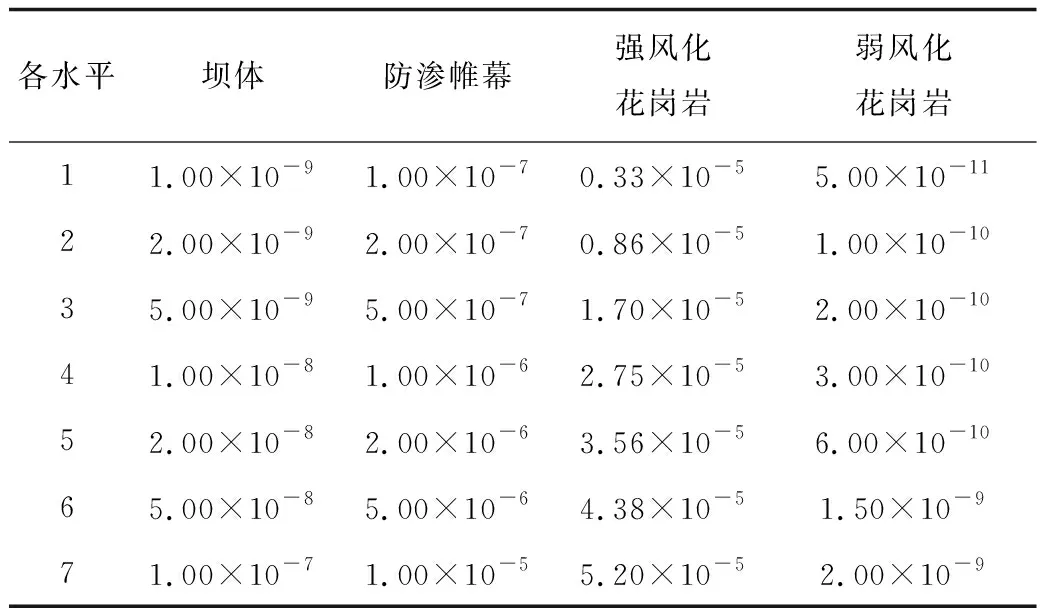
表2 基于正交设计参数各水平取值Table 2 Values of each level based on orthogonal design parameters m/s

变异概率为0.01。由图6可知，GA-BP神经网络可以较好地预测该混凝土坝各介质的渗透系数，由此可以确定渗透系数和扬压力、渗流量之间的非线性映射关系。

为获得绝对渗透系数，应当同时使用扬压力和渗流量监测数据来进行渗透系数反演研究。由于该混凝土坝渗流量的监测值是若干个坝段渗流量之和，为解决这一问题，本文使用单宽渗流量来开展渗透系数反演研究。将2015年1月3个渗压计的实测数据11.47，0.14，-1.63 m和单宽渗流量3.57×10-4L/(s·m)(单宽渗流量使用量水堰WE3与对应监测坝体宽度的比值)代入已训练好的神经网络进行渗透系数反演，反演结果见表1。

2.3 结果验证

为了验证反演渗透系数的准确性，选取2013年8月1日-2015年7月31日时间段内的上下游水位作为模型上下游水位边界条件进行有限元模拟，计算渗压计UP9，UP10和UP12的扬压力、量水堰WE3单宽渗流量，并将预测结果与该时间段内的实测值分别对比分析。

2.3.1 扬压力对比验证

渗压计UP9，UP10和UP12的扬压力的预测值和实测值之间的对比如图7～9所示。由图可知，扬压力预测值表现出明显的年周期变化规律，与实测值整体上基本吻合。渗压计UP9预测值与实际值之间的相对误差在-0.4%～0.92%内，总体上控制在1%以内。在2013年11月份内，预测值和实测值之间的相对误差相比其他时间点偏大，相对误差为2.28%。渗压计UP10预测值与实测值之间的相对误差在-9.92%～8.75%内。在2014年12月的相对误差偏大，为-18.57%，但预测值和实测值之间相差仅为0.013 m，误差较小，总体上可以较好的预测该渗压计的扬压力。渗压计UP12预测值与实测值之间的相对误差在-22.03%～22.7%内，在2014年2月和2015年2月2个时间点误差偏大，分别为51.68%和53.44%，预测值和实测值之间相差分别为0.39 m和0.31 m，较UP9和UP12扬压力误差偏大，但总体上来看渗压计UP12的扬压力可以较好地预测。

图6 渗流反演结果相关性Fig.6 Correlation of seepage inversion results

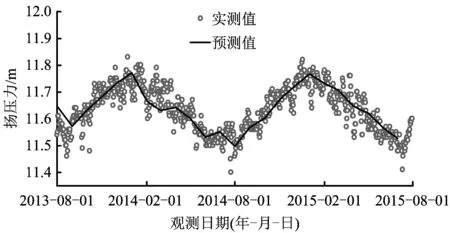
图7 渗压计UP9扬压力预测值和实测值对比Fig.7 Comparison between predicted values and measured values of uplift pressure by osmometer UP9

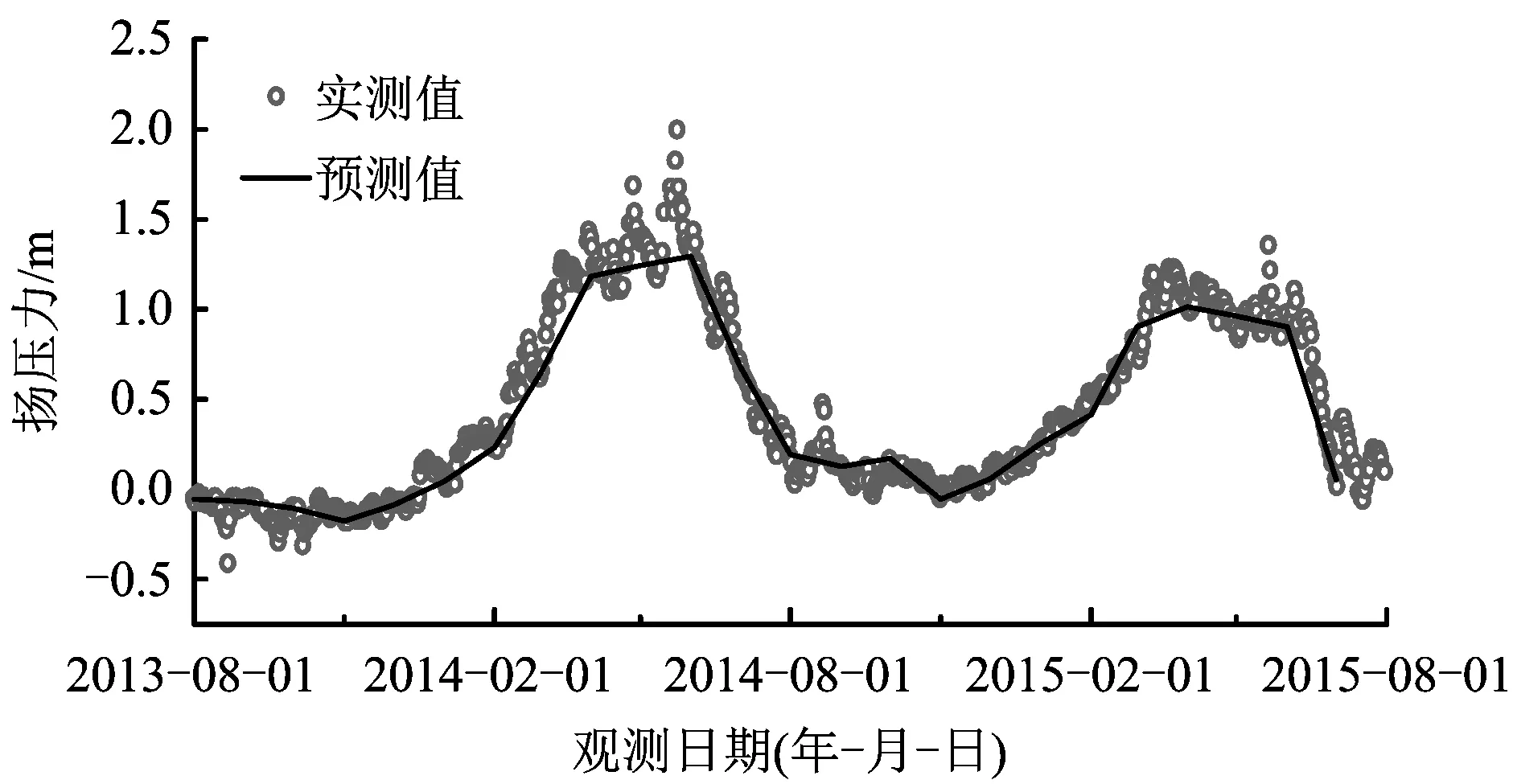
图8 渗压计UP10扬压力预测值和实测值对比Fig.8 Comparison between predicted values and measured values of uplift pressure by osmometer UP10

2.3.2 渗流量对比验证

单宽渗流量实测值和预测结果的对比如图10所示。由图10可知，单宽渗流量预测值与实际渗流量变化规律一致，表现出明显的年周期变化特征，与单宽渗流量实测值基本吻合，两者之间的相对误差在-17.50%～26.92%，总体上两者的相对误差控制在25%以内。2014年3月和4月，单宽渗流量实测值和预测值相对误差较大，分别为-21.42%和32.00%，而两者之间的差值仅为2.87×10-4L/(s·m)和1.03×10-4L/(s·m)。总体上来看，大坝各介质渗透系数反演值可以较好地预测渗流量的变化趋势。

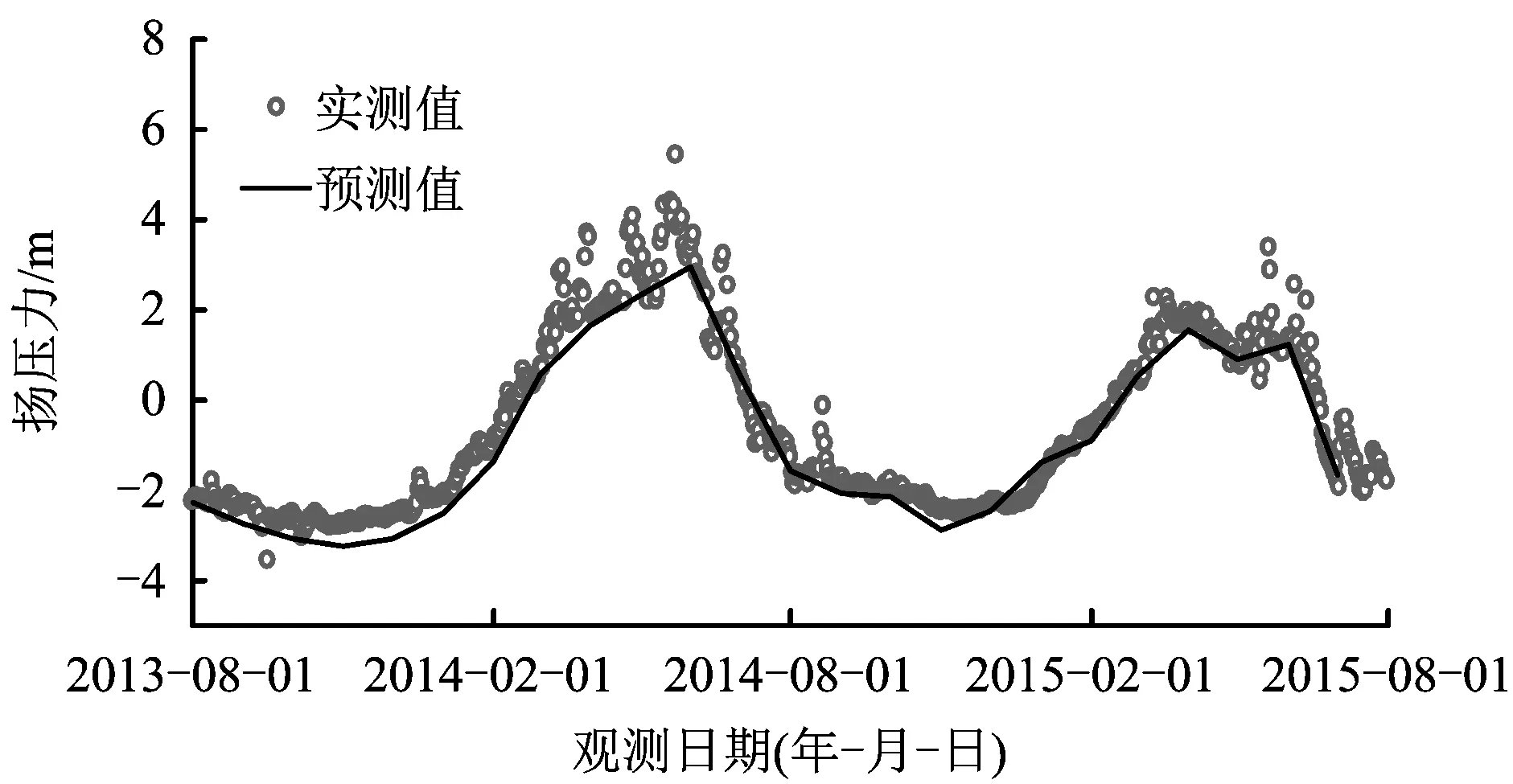
图9 渗压计UP12扬压力预测值和实测值对比Fig.9 Comparison between predicted values and measured values of uplift pressure by osmometer UP10

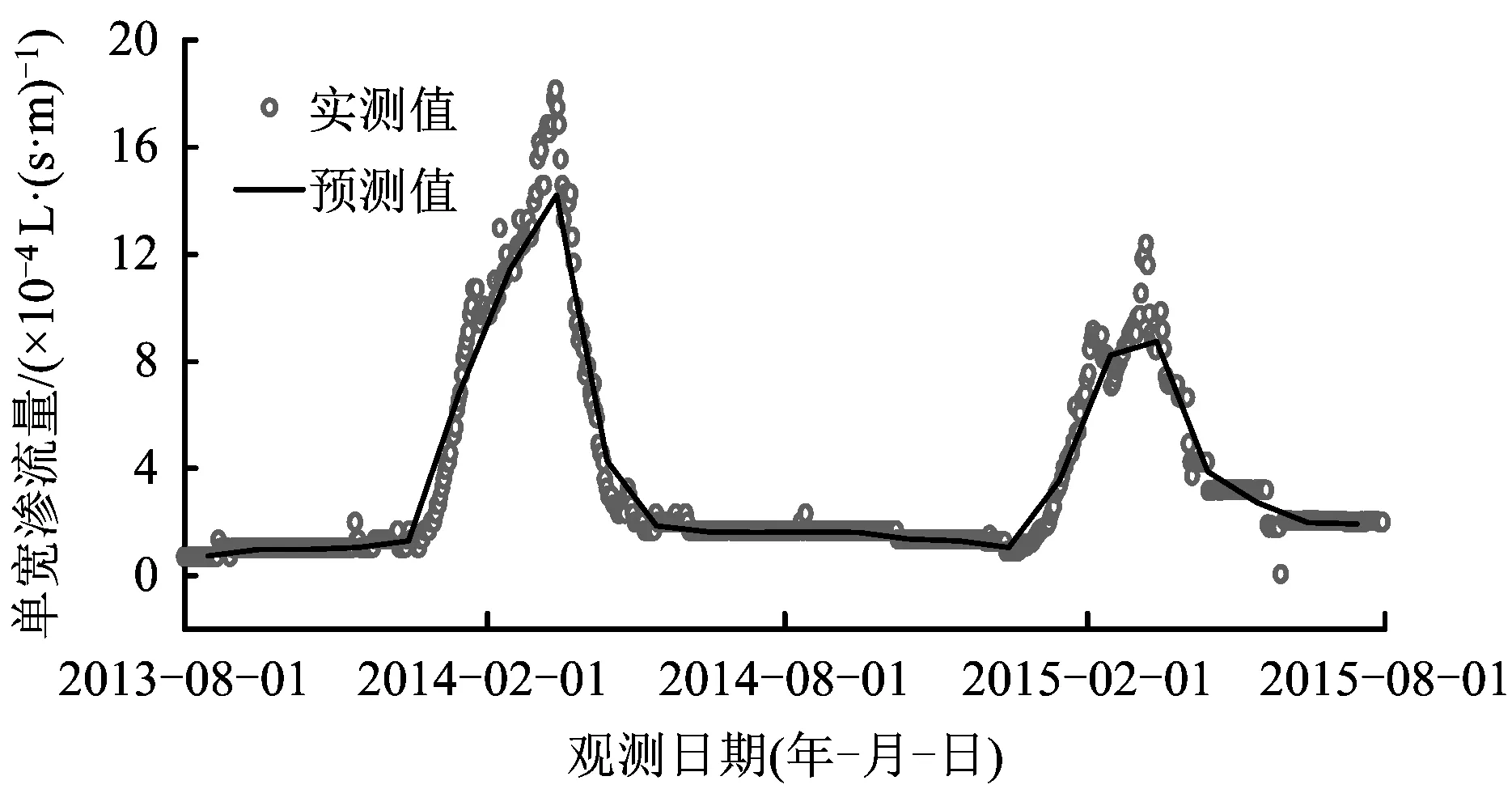
图10 引水坝段单宽渗流量预测值和实测值对比Fig.10 Comparison between predicted and measured values of unit width seepage quantity in diversion dam section

3 结论

1)采用正交设计、有限元正分析和GA-BP神经网络相结合的分析方法，建立了以渗压和渗流量监测时间序列为反演目标的渗透系数反演分析模型，可以较好地解决单目标反演的缺陷，反演结果唯一。

2)基于渗流监测数据，大坝坝体、防渗帷幕、强风化花岗岩以及弱风化花岗岩渗透系数反演值分别为1.17×10-8，1.09×10-6，2.21×10-5，3.46×10-10m/s，反演值与其理论值之间的相对误差分别为17.41%，9.20%，-18.11%和15.30%，总体上渗透系数的相对误差控制在20%以内。

3)开展了扬压力和渗流量预测结果与实测数据对比分析，渗压计UP9，UP10，UP12预测值与实际值之间的相对误差分别控制在-0.4%～0.92%，-9.92%～8.75%，-22.03%～22.7%内，单宽渗流量相对误差控制在-17.50%～26.92%内。扬压力、单宽渗流量预测值均表现出明显的年周期变化规律，与实测值整体上基本吻合，反演结果可靠。