稠油油藏双管水平井注汽井筒参数预测新模型
2019-09-06张艳玉孙晓飞陈会娟
李 朋,张艳玉,孙晓飞,陈会娟, 刘 洋
(1.中国石油大学(华东),山东 青岛 266580;2.上海大学,上海 200072;3. 中国石油勘探开发研究院,北京 100083)
0 引 言
受油藏非均质性及井筒内流体变质量流特性等影响[1-7],常规单管注汽“跟趾效应”明显,严重制约着地层均匀受热和油藏的动用效果[8-9]。针对该问题,部分学者提出双管水平井趾端注汽技术[10-11],以改善水平段油藏动用均匀程度,因此,研究双管水平井井筒沿程关键参数分布规律具有重要意义。目前,水平井井筒沿程关键参数预测模型主要包括解析模型和数值模型。在解析模型领域,林日亿等[12-14]对水平井井筒内蒸汽传热与传质规律进行了研究,但忽略了油藏物性随时间变化的影响。在数值模型领域,Stone[15]首次建立了常规单井油藏与井筒耦合黑油模型;Siu等[16]考虑同心双管管柱结构特点,建立了单井循环注汽数学模型;陈会娟等[17-19]模拟了常规单管井筒入流规律,但模型未考虑井筒和地层之间传热的影响。因此,基于双管水平井管柱结构特点,考虑井筒与地层传热的影响,建立水平井井筒与油藏耦合数学模型,以此为基础,研究井筒沿程关键参数分布规律,为指导现场开发提供理论依据。
1 数学模型建立
1.1 基本假设
数学模型基本假设条件如下:①油藏内油、汽、水三相为非等温渗流,满足达西定律,且油、汽、水三相相对渗透率及黏度受温度影响;②考虑重力和毛管力的影响,热量以热对流和热传导方式实现;③注汽井跟端的注汽参数恒定不变;④热流体向筛管外缘传热为稳态传热,筛管外缘到油藏传热为非稳态传热。
1.2 油藏内渗流与传热数学模型
该模型主要由油相质量守恒方程、水相质量守恒方程、蒸汽相质量守恒方程、能量守恒方程以及蒸汽相热平衡方程组成。
油相质量守恒方程为:
(1)
水相质量守恒方程为:
(2)
蒸汽相质量守恒方程为:
(3)
式中:下标o、w、g代表油、水、蒸汽三相;μ为黏度,Pa·s;Kr为相对渗透率;K为储层渗透率,mD;t为时间,s;ρ为密度,kg/m3;p为压力,Pa;g为重力加速度,m/s2;q为单位时间内流入和流出微元体的流体质量,kg/(m3·s);S为饱和度;mc为蒸汽凝结成水的质量,kg/(m3·s);φ为孔隙度;H为流体的焓,J/kg。
考虑井筒与油藏传热的影响,对前人模型[17-19]进行修正,得到能量守恒方程为:
(4)
式中:T为油藏温度,℃;λR为油藏导热系数,W/(m·℃);ρR为岩石密度,kg/m3;CR为油藏岩石比热容,J/(kg·℃);U为流体的内能,J/kg;Qs、Qloss分别为单位时间内注入微元体的能量和油藏向顶底层散失的能量,J/(m3·s);Ql、Qa分别为长管和环空内蒸汽向油藏传递的热量,J/s。
蒸汽相热平衡方程为:
lnps=23.20311-3826.36/(Ts+227.68)
(5)
式中:ps为饱和蒸汽压力,Pa;Ts为饱和蒸汽温度,℃。
模型求解所需辅助方程、初始条件及边界条件参考文献[18]。
1.3 井筒内流动与传热数学模型
1.3.1 长管内流动与传热数学模型
长管注汽短管排液(长注)以长管跟端为坐标原点,短管注汽长管排液(短注)以长管趾端为坐标原点,蒸汽在长管内流动时无质量损失,其质量守恒、动量守恒和能量守恒方程分别为:

(6)
(7)
(8)
(9)
式中:m1为单位时间内长管内蒸汽质量,kg/s;dl为微元段长度,m;ρ1为长管内蒸汽密度,kg/m3;v1为长管内蒸汽流速,m/s;p1为长管内蒸汽压力,Pa;θ为井筒与水平线夹角,rad;τ1为长管内壁摩擦力,N;h1为长管内蒸汽的焓,J/kg;R1为长管内壁到油藏的总热阻,(m·K)/W;T1、Te分别为长管内蒸汽温度和长管微元段对应的地层温度,℃。
1.3.2 环空内的流动及传热数学模型
长注以环空趾端为坐标原点,短注以环空跟端为坐标原点,环空内蒸汽流动的质量守恒、动量守恒和能量守恒方程分别为:

(10)
(11)
(12)
(13)
式中:ma为单位时间内环空内蒸汽质量,kg/s;rai为筛管内半径,m;ρa为环空内蒸汽密度,kg/m3;va为环空内蒸汽流速,m/s;pa为环空内蒸汽压力,Pa;τa为筛管内壁摩擦力,N;ha为环空内蒸汽的焓,J/kg;var为环空内蒸汽径向流速,m/s;maf为油藏吸汽率,kg/(m·s);Ra为环空内壁到油藏之间的总热阻,(m·K)/W。
由式(6)—(13)可得长注和短注过程中长管和环空内蒸汽压力和干度分布,结合式(5)即可求得长管及环空内任意位置处蒸汽温度分布。
1.4 井筒与油藏耦合模型
水平井注汽过程中,井筒内的管流与油藏内流体的渗流既相互联系又互相影响,井筒与油藏内压力场可通过注汽量公式相耦合,即:
mg=ρaJ(pa-p)Is
(14)
式中:mg为单位时间油藏中注入的蒸汽质量,kg/s;J为注汽指数,m3/(Pa·s);Is为地层吸汽指数。
2 模型求解
由于油藏与井筒耦合模型为强非线性模型,为保证模型的收敛性,采用全隐式有限差分法及迭代技术对其进行求解:①设定长管和环空内蒸汽压力、温度和干度值;②利用稳定双共轭梯度法求解油藏内传热与传质数学模型[20];③在步骤②所得地层压力、温度、饱和度等值的基础上求解井筒传热与传质数学模型;④将步骤③求得的井筒内蒸汽压力、温度和干度代入油藏传热与传质数学模型中反复迭代计算,直到所求结果满足收敛条件,即得该时间步最新地层参数以及井筒参数;⑤重复步骤②、③、④,最终可得任意时刻地层内压力、温度、饱和度及井筒内蒸汽压力、温度和干度。
3 实例分析
以加拿大麦肯河稠油油藏某实验区块的地质与开发资料为依据,对所建模型进行验证,模型计算基本参数如下:油藏平均厚度为20 m,初始压力为0.22 MPa,初始温度为10 ℃,横向和垂向渗透率分别为2 700 、1 890 mD,孔隙度为0.33,含油饱和度为0.75,水平井跟端注汽压力为2.00 MPa,蒸汽干度为95%。
3.1 模型可靠性验证
为验证模型的准确性,将长注模型预测的日注汽量与现场数据及前人模型预测结果进行对比(图1)。由图1可知,模型预测结果与现场数据基本吻合,最大误差为7.05%,与前人模型预测结果相比,平均误差减小了37.42%,表明模型准确可靠。前人模型误差较大主要原因在于其模型中的能量守恒方程违背了能量守恒定律,低注汽速率条件下,地层受热主要源自井筒传递的热量[19]。当忽略井筒与油藏间传热时,地层吸热量减少,流体流动性减弱,注汽量减小。此外,相同注汽参数下,短注模型预测的日注汽量略高于长注模型,这是因为短注过程环空蒸汽压力较长注过程环空压力大。
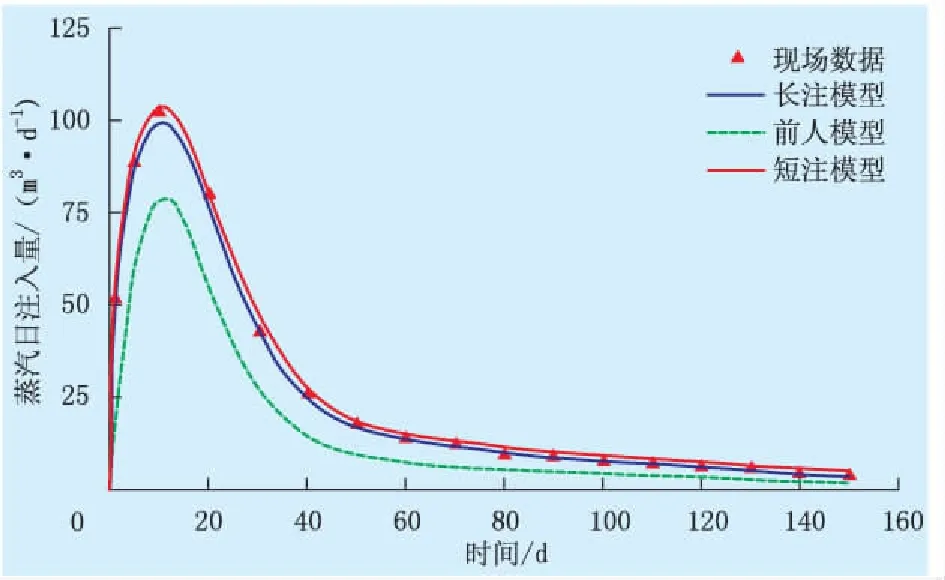
图1 水平井日注汽量预测结果
3.2 井筒沿程关键参数分布规律分析
基于新建数学模型,通过编制双管水平井注汽油藏数值模拟程序,对长注和短注过程中井筒沿程关键参数进行预测,预测结果如图2所示。由图2a、b、d、e可知,受长管内蒸汽摩擦损失、摩擦热损失和环空内蒸汽摩擦损失、摩擦热损失以及注入到地层蒸汽热损失的影响,长注过程蒸汽压力、干度从长管跟端到趾端、环空趾端到跟端和短注过程蒸汽压力、干度从环空跟端到趾端、长管趾端到跟端均不断降低。随时间增加,长注过程和短注过程井筒内蒸汽压力均先增大后减小,蒸汽干度均先减小后增大。这是由于2种注汽模式下注汽量均先上升后降低(图1),蒸汽注入量越大,井筒内蒸汽流量越小,摩擦损失越小,热损失越大。由图2c、f可知,长注过程和短注过程井筒内蒸汽温度和压力分布规律一致,这是因为饱和蒸汽温度是压力的函数。2种注汽模式下,长管内蒸汽压力和温度均呈线性变化,而环空内蒸汽压力和温度均为非线性变化,这是由于长管内蒸汽质量流量为定值,而环空内蒸汽质量为变量。此外,蒸汽压降和温度下降主要发生在长管内,这是由于长管管径较筛管小,蒸汽流速较大,摩擦损失大。

图2 长注和短注过程井筒内蒸汽热力参数分布
4 注汽效果优化
为优化油田注汽生产效果,对不同地层物性特征(井筒沿程地层均质、井筒跟端地层物性较好和井筒趾端地层物性较好)中不同注汽方式(长注与短注)在注汽初期(2 d)和后期(150 d)井筒沿程地层受热效果进行对比研究(图3)。为分析井筒沿程地层温度分布的离散程度和地层受热效果,采用标准差α和均匀系数β对注汽效果进行评价:
β=(α短注-α长注)/α短注
(15)
式中:α短注、α长注分别为短注和长注条件下水平段地层温度标准差;β为均匀系数,%。
表1为地层受热均匀程度。由表1可知,当井筒沿程地层均质和井筒跟端地层物性较好时,采用长管注汽短管排液方式,可减小井筒沿程地层温度分布离散程度,有利于地层均匀受热,在注汽后期,地层受热均匀程度可分别提高11.11%和26.74%;当井筒趾端地层物性较好时,短管注汽长管排液均匀预热效果更好,在注汽初期和后期,研究区地层受热均匀程度可分别提高52.24%和11.76%。
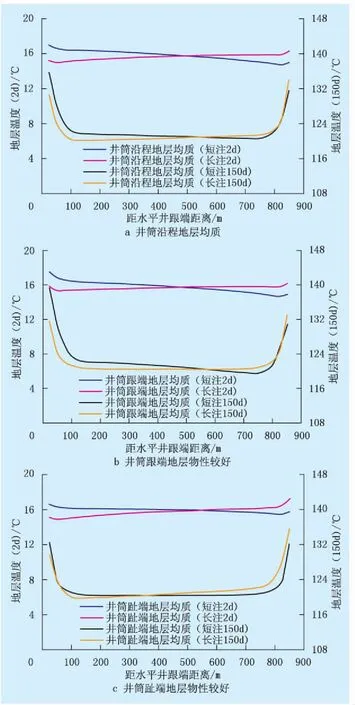
图3 不同地层物性特征下井筒沿程地层温度分布
5 结 论
(1) 建立考虑井筒到地层传热影响的双管水平井井筒与油藏耦合数值模型,新模型最大误差为7.05%,平均误差较前人模型减小37.42%,运用该模型可模拟井筒沿程蒸汽压力、温度和干度等关键参数分布规律。

表1 地层受热均匀程度评价
(2) 随时间增加,井筒内蒸汽压力和温度先增大后减小,蒸汽干度先减小后增大,且压降和温度下降主要发生在长管内。
(3) 注气后期,当井筒沿程地层均质和井筒跟端地层物性较好时,长管注汽短管排液预热效果好,地层受热均匀程度分别提高了11.11%和26.74%;当井筒趾端地层物性较好时,短管注汽长管排液均匀预热效果更好,地层受热均匀程度可提高11.76%。
