牛顿流体-幂律流体双区复合稠油油藏水平井热采试井模型

2019-09-06姜瑞忠崔永正张春光

特种油气藏 2019年4期

高岳，姜瑞忠，崔永正，张春光，潘红

(1.中国石油大学(华东)，山东青岛 266580；2.中国石油大港油田分公司，天津 300280)

0 引言

国内外大量实验研究发现，稠油黏度受温度影响显著。稠油在低温下黏度大，为非牛顿流体；在高温下黏度小，为牛顿流体[1-3]。前人在均质油藏模型中，将稠油处理为幂律流体，并求解其数值解[4-12]。近年来大量实验发现，在稠油油藏中，渗透率随着压力增加呈指数式降低，即在稠油油藏中存在应力敏感，并在各种稠油模型中将应力敏感的影响考虑其中[13-15]，但尚未有人提出同时考虑应力敏感和稠油幂律流体特征的水平井试井模型。因此，基于稠油水平井的幂律流体特性及渗透率应力敏感，考虑井筒储集和表皮效应的影响，建立牛顿流体-幂律流体双区复合稠油油藏试井解释数学模型，采用有限元方法进行求解，获得井底压力随时间的变化规律，绘制无因次压力及压力导数与无因次时间的双对数曲线，对各参数进行敏感性分析，并对实际生产数据进行拟合。

1 试井模型的建立

在水平井稠油热采的过程中，近井带注入蒸汽，稠油黏度随温度升高而降低，其流变性也由幂律流体转化为牛顿流体，而蒸汽未波及的远井带依然为冷油区，其流变性符合幂律流体特征[2]，因此，可将试井模型视作牛顿流体-幂律流体双区复合油藏。

数学模型假设为：①稠油油藏模型从内到外分为2个区域，内区蒸汽区为牛顿流体区，外区冷油区为幂律流体区，其中，内区半径为r1，两区的储层物性不同，渗透率各向异性；②模型外边界均为封闭边界；③岩石和孔隙内流体微可压缩，流体流动过程中温度恒定；④不考虑重力和毛管力的影响；⑤内、外区之间的界面没有额外的压力降；⑥外储层渗透率考虑应力敏感效应。

外区稠油黏度及储层渗透率[16-23]可表示为：

(1)

K=Kje-γ(pe-p)

(2)

基于上述假设条件，建立幂律稠油考虑压敏的水平井双区热采试井解释数学模型[24-27]：

内区牛顿流体：

(3)

外区幂律流体：

(4)

定义无因次变量：

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

式中：piD为无因次压力；Khi为水平渗透率，mD；pi为地层压力，MPa；pe为初始地层压力，MPa；μi为原油视黏度，mPa·s；Q为产量，m3/d；qD为无因次产量；B为地层原油体积系数，m3/m3；h为储层厚度，m；γ为导压系数，cm2/s；tD为无因次时间；φi为孔隙度，%；Cti为综合压缩系数，MPa-1；rw为井筒半径，m；t为时间，h；M12为内外区流度比；r1为内区半径，m；η12为内外区导压系数之比；Kvi为垂直渗透率，mD；x为横坐标值，m；y为纵坐标值，m；z为垂直坐标值，m；L为水平井水平段长度，m；xD为无因次横坐标；yD为无因次纵坐标；zD为无因次垂直坐标；γD为无因次应力敏感系数；rD为无因次半径：r1D为无因次内区半径；S为表皮系数；C为井筒储存系数；CD为无因次井筒储存系数；i=1为内区，i=2为外区。

模型定解条件如表1所示。

表1 定解条件

2 模型求解

建立双区复合稠油油藏水平井热采试井解释数学模型。应用Galerkin法[28-29]，取插值基函数N为权函数，得到试井模型的有限元方程。

内区：

(17)

外区：

(18)

利用Green公式分步积分：

(19)

有限元方程的矩阵形式为：

(20)

(21)

(22)

(23)

(24)

(25)

式中：pDn为不同节点无因次压力；n为水平井节点数量；Nk为形函数的分量，k=1，2，…，n；T为矩阵转置符号。

由式(20)—(25)可得：

KePn=Fe

(26)

(27)

(28)

由于水平井井筒内流体流动压力损失小，均匀流量模型误差较大，因此，选择无限导流能力模型进行求解，并借助均匀流量模型和无限导流能力模型的等压力点评价水平井井底压力，选取0.7L为水平井井底压力的等压力点。

应用Delta函数，将水平井划分为n个节点，得到无因次化后的单元源汇项有限元方程：

(29)

式中：fe为单元源汇项有限元方程；xD0、yD0、zD0为初始节点。

通过Stehfest反演，得到井底压力解：

(30)

3 压力响应特征及参数敏感性分析

3.1 压力响应特征

考虑渗透率压力敏感的稠油水平井热采试井曲线如图1所示，对应的流动阶段划分情况如表2所示。

3.2 参数敏感性分析

(1) 应力敏感系数对压力和压力导数曲线的影响如图2所示。由图2可知，无因次应力敏感系数γD对渗流过程的影响开始于内区径向流阶段，并且γD越大，地层应力敏感性越强，底层渗透率随压力变化而改变的幅度也越大，即在曲线上表现为γD越大，压力和压力导数值越大，曲线位置越高；随着渗流进行，压力波不断向边界传播，近井地带的压力梯度逐渐变大，渗透率降低的程度也越大，因此，后期的压力曲线和压力导数曲线比早期曲线上翘程度更明显。

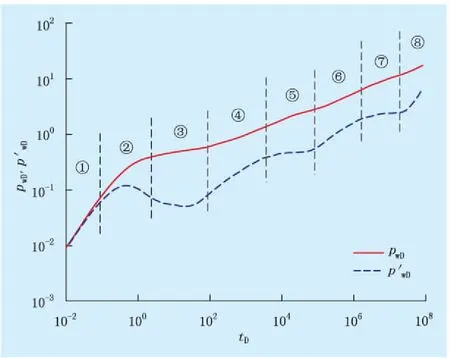
图1 双区复合稠油油藏水平井试井曲线

表2 流动阶段划分

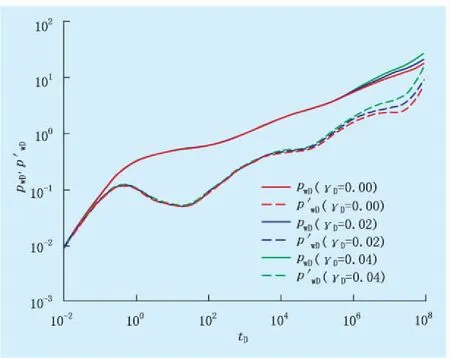
图2 应力敏感系数对水平井压力响应曲线

图3 幂律指数对水平井压力响应曲线

(3) 导压系数η对压力响应曲线的影响如图4所示。由图4可知，内区(牛顿区)与外区(幂律区)导压系数之比越大，幂律区反应特征越明显，压力导数曲线上翘程度越大，当η12=1时，曲线退化为单区模型曲线。

图4 内外区导压系数比对水平井压力响应曲线

(4) 内区半径对压力响应曲线的影响程度如图5所示。由图5可知，内区(蒸汽区)半径变小，压力波在内区中传播的时间变短，即内区径向流结束时间也越早。

图5 内区半径对水平井压力响应曲线

4 实例应用

新疆地区G油田某蒸汽吞吐井油层厚度为10.4 m，油层中部深度为168.7 m，孔隙度为0.28，井筒半径为0.09 m，原油黏度为7 200 mPa·s，水平井有效长度为99.8 m，注汽温度为140 ℃，蒸汽密度为1.095 874 kg/m3，综合压缩系数为0.003 54 MPa-1，日注汽量为59 t/d。通过验证发现，幂律指数取0.65拟合程度较好，可知内区半径为97.6 m，表皮系数为2.02，渗透率为2 254 mD，井筒储存系数为0.186 m3/MPa。

对比双区复合稠油油藏水平井试井模型与传统未考虑压敏及稠油幂律特性模型(图6)可知，双区复合稠油油藏水平井试井模型在后期拟合精度更高，表征出因幂律特性而导致的外区径向流阶段上翘特征，因此，该模型在稠油热采开发中有更好的适应性。