多井系统复合油藏平均地层压力计算方法研究

尹洪军，文 刚，邢翠巧，付 京，Perapon Fakcharoenphol

(1.东北石油大学， 黑龙江 大庆 163318；2.提高油气采收率教育部重点实验室， 黑龙江 大庆 163318；3.Mewbourne School of Petroleum & Geological Engineering， The University of Oklahoma， Oklahoma Norman OK， USA 73019；4.Colorado School of Mines， Golden Colorado， USA 80401)

0 引 言

平均地层压力是油田开发设计的一个重要参数，准确地分析出单井控制区域内的平均地层压力水平是油田保持高产、稳产，进行各种措施调整的必要条件[1-3]。常用的确定平均地层压力方法有MDH法、MBH法、迪茨(Dietz)法等[4-8]以及一些经验公式，这些方法只适用于均质油藏平均地层压力的计算，未考虑储层的非均质性，也未考虑到注采比的影响。但是在油田全面投入开发之后，随着井网加密和注水开采[9-12]，地下渗流状况较油田开发早期发生了很大变化，注采不平衡使得油藏压力受到注采比的影响[13]。实际油藏中井周围储层存在径向复合储层情况，近些年研究的考虑邻井影响的平均地层压力计算方法并不实用。因此，需要建立多井系统复合油藏的拟稳定流渗流数学模型，给出考虑注采比影响的多井系统复合油藏平均地层压力的计算方法，保证多井注采情况下复合油藏的压力评价更符合实际情况。

1 理论基础

1.1 基本假设

无限大、等厚储层中存在微可压缩、黏度为常数的油水的流动；油水流度比为1，水平方向上的饱和度分布均一；储层中有多口生产井和注水井(也可能没有注水井)定量生产和定量注入，井的产量或注入量可以不同。在稳定生产时，每口井都自然地分成一定范围的供给区域，如两区复合油藏供给区域分为2个区域。关井前供给边界或供给区域内的压力随时间变化具有某种上升或下降趋势。两区复合油藏物理模型如图1所示。

1.2 数学模型的建立和求解

根据物质守恒原理可得：

(1)

在线性压力趋势条件下，即t≥tpss(tpss为拟稳态出现时间，h)[14]，有：

(2)

图1 两区复合油藏物理模型示意图

将式(2)代入式(1)得：

(3)

生产井的供给区域是以该井为中心的圆形两区复合区域，建立线性压力趋势下的径向流动数学模型：

(4)

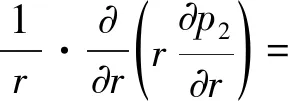
(5)

内边界条件：

p(rw，t)=pwf(t)

(6)

外边界条件：

(7)

两区界面条件：

p1(a，t)=p2(a，t)

(8)

(9)

式中：pwf为井底流压，MPa；p1、p2分别为1区和2区的地层压力，MPa；μ为流体黏度，mPa·s；K1、K2分别为1区和2区的渗透率，D；r为地层某点到井底的距离，m；rw为井底半径，m；a为复合半径，m；re为边界半径，m。

求解数学模型式(4)—(9)，得到两区复合油藏的地层压力公式：

(10)

(11)

其中：

(12)

(13)

C1=λ[-Y2(1-RIP)a2+C]+Y1(1-RIP)a2

(14)

(15)

(16)

1.3 复合油藏平均地层压力公式

用面积加权方法计算两区复合油藏单井平均地层压力：

(17)

将式(10)和式(11)代入式(17)，整理得：

(18)

式(18)即为两区复合油藏的平均地层压力计算公式。

当RIP=1时，式(18)转换为式(19)，即为注采平衡时的复合油藏平均地层压力公式，与水驱平均地层公式相同，从而验证了该方法的正确性。

(19)

2 平均地层压力敏感性分析

要获得多井系统复合油藏考虑注采比影响的地层压力，需利用油井压力恢复测试资料解释出该井控制区域内的储层参数。在给定油井基本参数(产量或注入量、生产时间、有效厚度、孔隙度等)和储层参数(渗透率、表皮系数等)情况下，当边界压力一定时，绘制出地层压力分布曲线，并计算出单井平均地层压力，基础参数见表1。

表1 基础参数表

图2～4分别为不同因素影响下的地层压力分布曲线。图中的水平线为每一条地层压力分布曲线对应的平均地层压力。

2.1 注采比对单井地层压力的影响

注采比分别为0.5、1.0和1.5，不同注采比条件下测试井地层压力分布如图2所示，对比结果见表2。

从图2可以看出：边界压力一定时，注采比越大，井底压力越大，平均地层压力也越大；在复合半径为62 m时，随着注采比的增大，内区与外区压力消耗速度变小，两区界面压力变化转折点不明显；井底附近压力消耗速度最大，外区渗透率比内区低，外区压力消耗速度较大。由表2可知，随着注采比的增大，井底附近的压力消耗速度减小，井底流压增大。注采比大于1时，计算的平均地层压力大于注采平衡时的平均地层压力。一般油田注采比大于1，要得到准确的平均地层压力，需要考虑注采比影响。

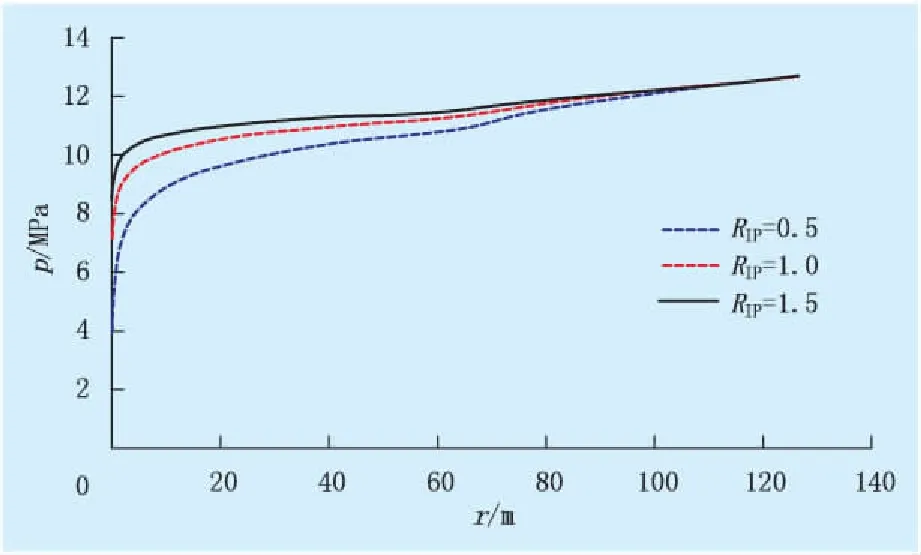
图2 不同注采比条件下单井地层压力分布曲线

注采比井底流压/MPa平均地层压力/MPa0.53.98411.7711.07.12211.9691.58.69112.069

2.2 流度比对单井地层压力的影响

外区与内区的流度比(M)分别为0.22、0.32和0.42，其他参数一定时，不同流度比条件下测试井地层压力分布如图3所示，对比结果见表3。

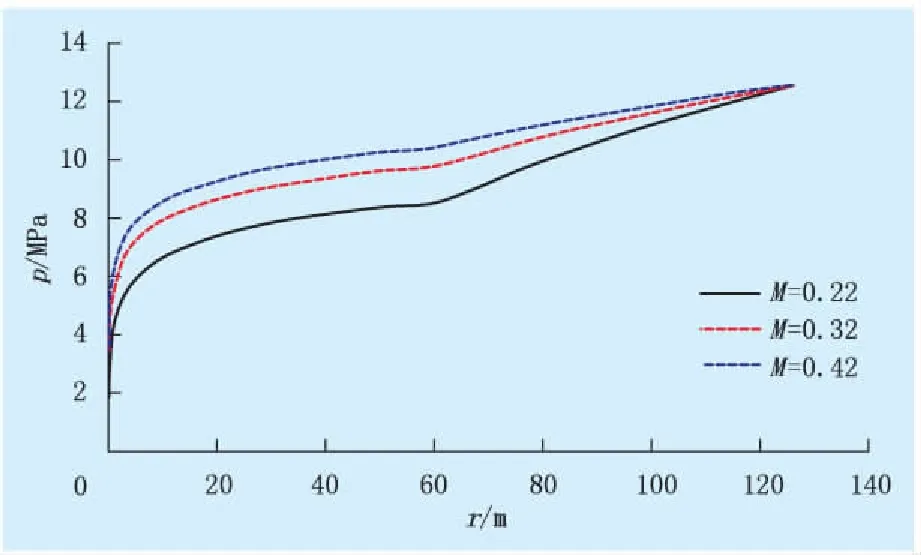
图3 不同流度比条件下单井地层压力分布曲线

流度比井底流压/MPa平均地层压力/MPa0.221.88510.6820.323.12611.2450.423.77711.539

由图3可知：边界压力一定时，流度比越大，生产井附近的压力消耗越小，注采井间的压差越小；受到非均质性影响，在复合半径为62 m处出现压力变化转折点；外区渗透率越小，压力消耗速度越大。由表3可知：随着流度比的增加，井底流压和单井平均地层压力依次增加，单井平均地层压力的增加速度变小。

2.3 复合半径对单井地层压力的影响

复合半径分别为62、73和88 m，其他参数一定时，不同复合半径条件下测试井地层压力分布如图4所示，对比结果见表4。

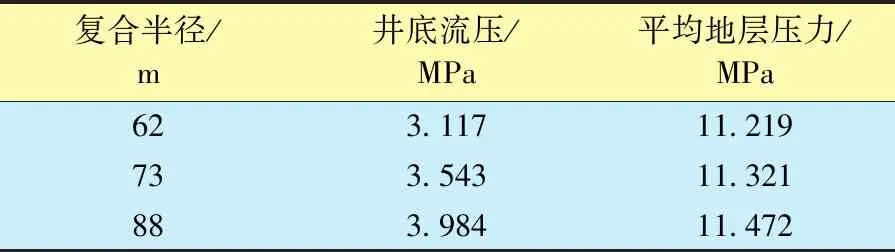
复合半径/m井底流压/MPa平均地层压力/MPa623.11711.219733.54311.321883.98411.472

由图4和表4可知：边界压力一定时，其他参数不变情况下，随着复合半径的增加，生产井的井底流压和平均地层压力都在不断上升；不同复合半径的外区地层压力分布水平一致，复合半径主要影响地层压力分布曲线上翘时间；复合半径越小，外区性质越差时，流体在内区流动时间越短，地层压力分布曲线上翘时间越早。

3 实例应用

以喇嘛甸油田某口井为例，单井控制面积为0.1 km2，油层有效厚度为2.2 m。井周围受到多口注水井影响，稳定生产0.5a后关井测压力恢复，关井时间为71.333 h。日产液量为72.14 m3/d，含水为97.2%，流体黏度为0.835 2 mPa·s，油层中部流压为4.099 MPa。利用曲线拟合方法解释实测(lgΔp，lgΔp′)-lgt双对数曲线(Δp为关井不同时刻压差值，MPa；Δp′为关井不同时刻的压力导数值，MPa/h)，双对数曲线拟合结果如图5所示。根据拟合得到的参数，利用公式(19)计算出该井控制范围内的平均地层压力为11.250 MPa，拟合参数和压力计算结果见表5。注采比为1.30，地层存在多余能量补充，关井测得的末点压力明显大于实际平均地层压力水平，注采平衡的水驱平均地层压力则会偏小；实际计算的平均地层压力(11.250 MPa)小于关井末点压力(11.565 MPa)，同时大于不考虑注采比影响的水驱平均地层压力(10.570 MPa)，说明考虑注采比影响，计算得到的平均地层压力更符合实际地层压力水平。

图5 双对数曲线拟合结果

参数数值渗透率/mD0.064复合半径/m71.45流度比0.676表皮系数-1.370注采比1.30平均地层压力/MPa11.250末点压力/MPa11.565水驱平均地层压力/MPa10.570

4 结 论

(1) 根据物质平衡原理，建立考虑注采比影响的多井系统复合油藏拟稳定渗流数学模型，并给出了平均地层压力的计算方法。该方法适用于考虑注采比影响的多井系统复合油藏单井控制区域平均地层压力的计算。

(2) 单井平均地层压力的主要影响因素为：产量、渗透率、地层厚度、复合半径和注采比。边界压力一定时，注采比越小，井间注采压差越大，井底流压和平均地层压力越小；流度比越小，地层能量消耗越大，井底流压和平均地层压力越小；复合半径影响内外区地层压力分布上翘变化时间，外区地层各点压力分布重合。

(3) 通过考虑注采比参数，可以更好地认识多井系统受到邻井影响后的地层压力水平。注采比大于1，地层有多余能量补充，关井测得的末点压力明显大于实际平均地层压力水平，水驱平均地层压力则会偏小，因此，该方法计算的平均地层压力介于末点压力和水驱平均地层压力之间，更符合实际。