基于属性相容性的随机森林算法

刘 毓, 刘 陆, 高 尹, 杨 柳

(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)

随机森林算法[1]具有较低泛化误差和较好收敛性，可解决决策树的局部最优解和过度拟合问题，已成为数据分析、图像处理、知识管理等众多领域的研究热点之一。

随机森林算法的基分类器为决策树[2]，改进单个基分类器的分类准确率可以提高整个随机森林算法的分类准确率。通过遗传算法寻找参数最优组合的方法，提高了算法的分类性能，但算法的收敛速度依赖于初值设定[3-4]。给抽样结果增加约束条件，非平衡数据的分类性能有所提高，但是算法训练速度较慢[5]。采用决策协调度作为划分规则分裂节点，根据条件属性与目标属性等价类模的比值衡量该属性的分类能力，虽然基分类器的性能有一定的提升，但仍然存在模糊问题[6]。因此，针对上述问题，本文以决策协调度为基础，从条件属性与目标属性间的逻辑关系入手，引入粗糙集理论[7]中属性相容性[8]，以条件属性的相容度作为基分类器分裂节点的准则，用宽相容度辅助严相容度构建基分类器，以期提高基分类性能，进而改善随机森林算法性能。

1 随机森林算法基本原理

随机森林算法根据Bagging抽样模型[9]，采用有放回的随机采样方式进行采样，生成K个子训练集，再从每个子训练集的所有属性中选取特征子空间[10]。特征子空间的大小影响了随机性的引入程度，一般取值为 log2M+1，M为特征总数。将选取特征子空间后的K个子训练集建立K个基分类器，从而形成随机森林，如图1所示。每个基分类器任其生长，不需要剪枝[11]。基分类器一般采用ID3[12]或C4.5[13]算法。当输入测试样本时，随机森林输出的分类结果由每个基分类器的输出结果进行简单投票决定。

图1 随机森林示意图

设随机森林模型为{h(X,θk),k=1,2,…,K}，其中，h(·)为单个基分类器，K为基分类器的总个数，X为样本条件属性集，θk为基分类器参数。样本集为T={(xi,yi):xi∈X,yi∈Y,i=1,2,…,N}，其中N为样本容量，Y为决策属性。

输入样本X对应的正确分类结果Y的得票数，超过其他错误分类别中得票数最多者的程度可用余量函数表示为

(1)

其中，I(·)为指示函数，当·为真时，取值为1;当·为假时，取值为0。

根据随机森林投票的特点，对给定样本分类的错误率的度量，利用泛化误差[14]表示为

e=P[m(X,Y)<0]。

(2)

其中，P(·)为概率质量函数。

式(2)结合Hoeffding不等式[15]与Chebyshev不等式[16]，得到随机森林的泛化误差界[13]

(3)

2 属性相容度基础理论

对于基分类器偏向选择多值属性的问题，可根据属性相容度进行改进，属性相容度以决策协调度为基础。

2.1 信息系统

决策表{U,A∪D,V,f}为一个信息系统[17]，其中U为全部对象的集合，为论域；A为条件属性集合；D为目标属性集合；V=∪a∈AVa是属性a的值域，即条件属性所有取值的集合；f:U×A→V为信息函数，它的作用是将U中所有对象的每个元素都映射为属性值，即∀a∈A,x∈U,f(x,a)∈Va。

2.2 等价关系与不可区分关系

信息系统可以简化表示为(U,R)，R为等价关系[18]，一个属性可以作为一个等价关系，信息系统可以看作是一个等价关系族。U/R表示一个等价类集，即所有元素在等价关系构成的集合。

设存在非空等价关系Z，Z是等价关系R的子集，各个子集Z的交集也是等价关系，此关系为不可区分关系，用O(Z)表示。在O(Z)下的等价类是信息系统中最小的单元。

2.3 决策协调度

等价类U/(A,D)表示条件属性集与目标属性集的交集，它的模用|A∪D|表示，作为一个测度显示A→D的逻辑关系强弱，也是决策规则出现的次数，即频度。决策协调度[17]的表达式为

(4)

其中，X是A的非空属性子集，|·|是求模运算。

属性决策协调度的值越大，则表示该属性重要程度越高。

3 基于属性相容度的改进算法

随机森林的性能取决于基分类器性能，基分类器的性能越高，随机森林的性能越强。改进算法以决策协调度为基础，从随机森林的基分类器入手。决策协调度只在宏观上做了处理，各个决策规则在相容关系上还有待提高，当各个条件属性间的协调度距离较小时，决策依据不足。因此，需先计算主决策集与次决策集，再构建属性相容度[18]，利用属性相容度作为划分规则。

3.1 主决策集与次决策集

设在决策表中存在条件属性集C∈A,O(C)={c1,c2,…,cm}与决策属性集D，O(D)={d1,d2,…,dL}，则在O(C,D)中，与决策规则C→di矛盾的集合是∪i≠jC→dj。依次对O(C,D)下的集合求模运算，模值最大集合为主决策集，记作W；模值次大的集合为次决策集，记作B。

3.2 属性相容度

设主决策集的模为|W|，次决策集的模为|B|，定义属性相容度的表达式为

(5)

其中，X为C的非空子集。B对W的影响为严相容度。

W与B间呈矛盾关系。当|W|与|B|的值相等时，将式(5)中次决策集舍去，属性相容度又可表示为

(6)

将次决策集舍去，只考虑主决策集的影响，则为宽相容度。

在比较属性相容度时，若严相容度相同且同为最大值，则需要进一步计算宽相容度并进行比较，从而将条件属性的性能严格区分。属性相容度也可以用决策规则出现的概率度量该规则逻辑关系的强弱，概率值越大，表示该条件属性与目标属性间的逻辑关系就越强，则该属性就越重要。主决策集与次决策集的定义都是与一个条件属性下的某个决策规则出现的频度有关。然而，这两个决策相互矛盾。在度量条件属性与目标属性逻辑关系强弱时，有必要将矛盾的规则剔除或是计算两者之差。对于一个条件属性而言，属性相容度越大，决策规则逻辑关系越强，分类能力越好。

3.3 改进算法步骤

通过严相容度与宽相容度的计算，能够区分不同条件属性，从而提高基分类器的分类能力。通过严相容度计算条件属性的分类能力就可以选择分裂节点。在特殊情况下，会出现条件属性严相容度相同的情形，且这些条件属性的相容度都大于其他条件属性相容度，此时计算宽相容度可将其区分。

算法的具体步骤如下。

步骤1 采用有放回的随机采样方式进行训练集采样，生成K个子训练集。

步骤2 取出1个子训练集，对该子集选取特征子空间，以此作为1个基分类器的训练集。

步骤3 基分类器训练开始，对训练集的数据初始化操作，将所有条件属性进行标记。

步骤4 分别计算出各个条件属性的主决策集的模值与次决策集的模值。

步骤5 利用式(5)计算所有条件属性的相容度。若存在两个的属性相容度的值近似且为最大值，则利用式(6)进行计算。

步骤6 选出分类性能最强的条件属性，并将该属性的标记去除，将该属性作为分裂节点加入生成模型来分隔样本集。

步骤7 重复步骤5和步骤6，直到所有属性都去除标记或达到叶子节点。

步骤8 生成并存储该基分类器模型。

步骤9 重复步骤2～步骤8，直至K个基分类器全部生成完毕，结束。

4 实验及结果分析

4.1 数据集选取

选取UCI公开数据集[19]中的Monks数据集、House-votes-84数据集、Credit-A数据集、Tic-tac-toe数据集和Kr-vs-kp数据集作为实验数据。其中，Monks数据集的样本数为432个，条件属性个数为6个。House-votes-84数据集的样本数为435个，条件属性个数为16个。Credit-A数据集的样本数为690个，条件属性个数为15个。Tic-tac-toe数据集的样本数为958个，条件属性个数为9个。Kr-vs-kp数据集的样本数为3 196个，条件属性个数为36个。以上5个数据集所有属性的取值均为离散值。

4.2 实验结果及分析

实验运行环境为中央处理器Intel (R) Core (TM) i3-3217U,主频1.8 GHz,内存4 GB的PC机, Win7 64位操作系统, Matlab版本9.0 (R2016b)。根据上述5种数据集，分别对比改进算法、随机森林算法[1]与文献[5]算法的准确率和运行时间，准确率对比结果如表1所示，运行时间对比结果如表2所示。

表1 准确率对比结果/%

从表1可以看出，改进算法对5种数据集的决策准确率均高于其他两种算法。在Monks数据集上，改进算法提高了近11%，比文献[5]算法提高了3.2%；在House-votes-84数据集上，改进算法提高5.5%，比文献[5]算法提高了2.7%。表明在训练数据量较少时，改进算法有明显的优势。这是由于改进算法充分利用了条件属性与目标属性的逻辑关系，采用属性的相容度作为分裂节点判决依据，从而得到更高的准确率。对于大数据集，改进算法的准确率也有所提高。

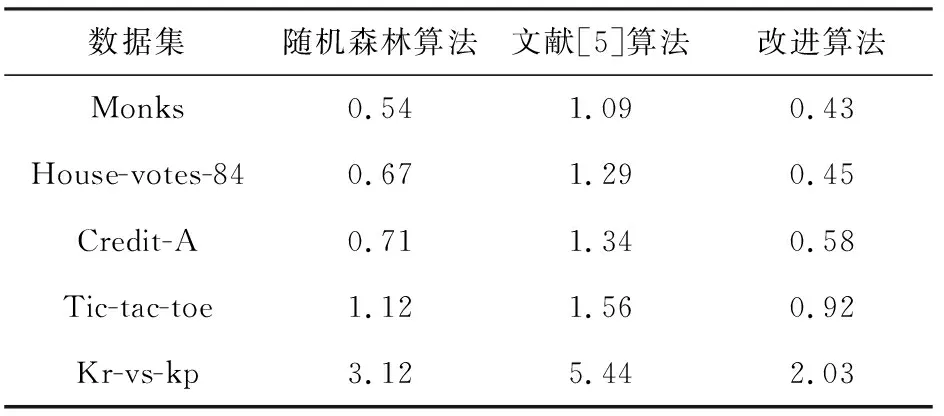
表2 运行时间对比结果/s

从表2可以看出，改进算法的计算复杂度均低于其它两种算法。改进算法继承了随机森林处理高维数据、特征遗失数据和不平衡数据的优点。

除了准确率外，查准率、查全率以及综合分类率以也是衡量算法性能的重要指标[20]。计算以上性能指标需要将样例的真实类别与预测类别的组合划分为真正例、假正例、真反例和假反例等4种情形[21]。

以Monks数据为例，3种算法对真实类别与预测类别组合划分的统计结果如表3所示。

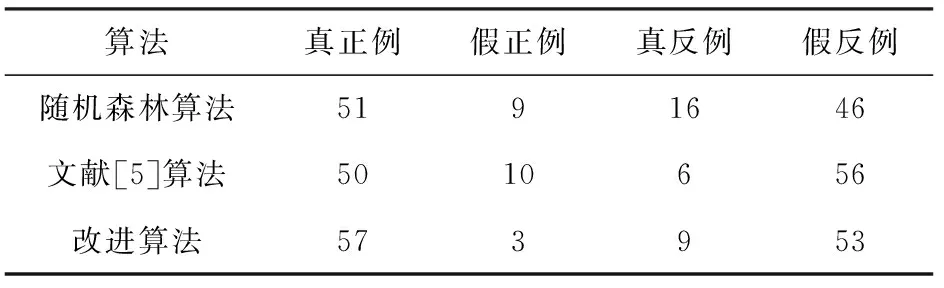
表3 3种算法统计结果

真正例与假反例的数量越多，算法的性能越好，从表3中可以看出不同算法分类结果的个数。但仅凭个数，无法准确描述算法的优劣，还需要进一步对比查准率、查全率和综合分类率等3种性能，结果如表4所示。

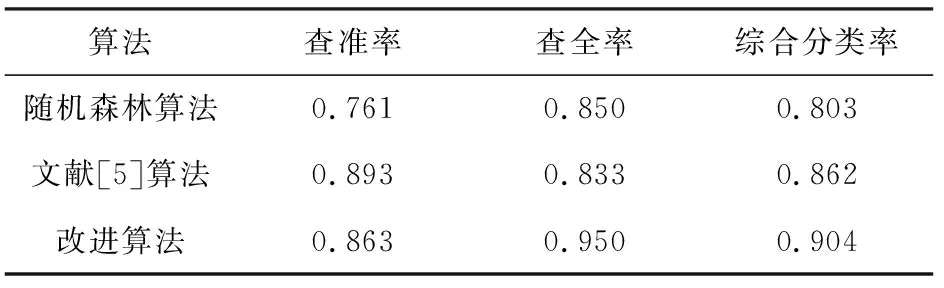
表4 3种算法性能对比结

从表4可以看出，改进算法综合性能最好，在查准率保持一定的情况下，查全率得到很大的提升，95%有用信息被留下。对于处理海量数据时，引入粗糙集的改进随机森林算法只需要计算各个等价类交集的模值，省去大量对数运算，降低计算的复杂度，提高训练速度，从而提高学习效率。

5 结语

基于属性相容度的随机森林算法，重新构建了用以度量条件属性的重要程度数学表达式，引入了属性相容性，并用属性的相容度代替传统算法中的信息增益作为新的划分规则，从而提高了基分类性能，改善了随机森林算法性能。实验结果表明，改进算法对数据量较少时具有更高的准确率，并且弱化了多值偏向问题，此外也不需要进行对数运算；在处理海量数据时，具有更快的训练速度。改进算法在继承了随机森林优点的前提下，不仅提高了预测准确率而且降低了计算复杂度。