超密集组网多维资源联合调度
2019-09-05孙长印金少卓谢永斌
孙长印, 金少卓, 谢永斌
(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
超密集网络(ultra dense network,UDN)[1]作为5G通信的关键技术之一,通过在蜂窝热点地区增加低功率站点的部署密度,可有效提升系统容量,并降低时延及能源消耗[2]。然而,宏基站之间存在同层干扰,低功率基站的部署又增加了宏基站与小功率基站之间的跨层干扰,以及小功率基站之间的同层干扰,使得干扰成为异构网络中影响系统性能的主要因素。资源分配技术是克服系统间干扰的有效解决方法,通过配置每个用户的关联小区、最优子载波以及最佳功率分配,可实现多维无线资源的联合优化,从而减轻系统间干扰,提高网络吞吐量,降低系统能耗[3-5]。
多重禁忌搜索[6]和模拟退火[7]资源分配方案可以避免方案陷入局部最优陷阱,实现能源效率的最大化。低复杂度的贪婪协同调度方案[8]以及联合功率控制和用户调度方案[9]实现了用户公平性与能效之间的良好平衡。协作调度方案[10-11]可解决多维资源联合优化时高耦合问题。但是,上述方案大都只考虑单一的优化目标,而在复杂网络环境下,往往需要考虑多用户多维资源多种目标函数联合优化的耦合问题。
本文研究在超密集异构网络下多用户多维资源多种目标函数联合优化问题。通过构建反映多系统效用的优化目标函数,分析不同权重下系统能效与谱效的耦合关系,构造反映速率约束以及成本代价函数[12]的惩罚项,以期提高系统性能和解的有效性。
1 系统模型
5G无线网络的部署将传统的蜂窝系统转变为具有多种不同类型节点的超密集异构组网,增加了网络管理的灵活性。在超密集异构组网中,采用控制面和用户面(C-Plane/U-Plane,C/U)分离[13-14]的网络结构,将控制面和用户面分离开,C平面由宏基站低频段控制,U平面由高频段控制。控制基站(control base station,CBS)提供覆盖和支持有效的无线资源控制过程。数据基站(data base station,DBS)在CBS的覆盖区域中提供高速率数据传输。超密集组网C/U分离网络的拓扑结构如图1所示。
假设在超密集异构组网中,每个宏蜂窝包含1个宏基站以及B个微基站,宏蜂窝覆盖范围内所有用户的数量为Y,下行信道总带宽为10 MHz,对应的时频资源块个数为K,资源块的带宽为w,则用户n在基站b的子载波k上的信干噪比[6]可表示为
(1)
其中gnkb为用户n在基站b的子载波k上的增益,βk为子载波k上的功率控制因子,Pmax为系统最大额定功率,PI为用户n受到的干扰功率,N0为热噪声密度。用户n在基站b的子载波k上的传输速率[6]可表示为
rnkb=ρnkbwlog2(1+γnkb),
(2)
式中,ρnkb为资源块的状态变量。若用户n占用了基站b的子载波k,则设ρnkb=1,否则,ρnkb=0。系统能效与谱效[15]的表达式分别为
β为所有子载波上功率控制因子的集合。以最大化系统的能效与谱效的权值和为目标,建立目标优化函数
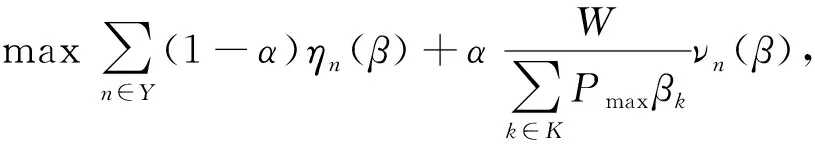
(3)


图1 超密集网络C/U分离网络结构
2 联合资源优化方案
引入模拟退火算法与列文伯格(Levenberg-Marquard,LM)功率分配[15]循环迭代机制,对用户关联、子载波分配以及功率控制等多维资源进行分配,追求系统目标函数即能效与谱效权值和的最大化。将目标函数式(3)中的约束问题转化为无约束问题。依据收益越大惩罚越大的准则,构造基于干扰的惩罚函数
θ(β)=[min(r-rmin)]2+
[min(c-P,0)]2,
(4)
其中,P为当前分配功率,c为成本代价函数,且
其中,g是信道增益,I是干扰,N是噪声。
将式(4)引入目标函数式(3),则目标函数更新为
(5)
其中λ为惩罚项的惩罚因子,且λ∈(0,1)。
直接求解式(5)较为复杂,需进行分步优化。采用两步的策略,第一步,首先在等功率的状况下采用基于模拟退火的随机调度算法寻找最佳用户关联以及子载波分配;第二步,在基于上述分配的基础上,采用列文伯格算法优化子载波的传输功率,最后循环迭代,直到目标函数收敛。算法流程如图2所示。

图2 联合资源分配算法流程
2.1 用户关联与子载波分配
对子载波进行等功率分配,采用基于模拟退火算法的随机调度策略进行用户关联以及分配子载波,获取此阶段的最优解。
为了进一步加速算法收敛速度,引入M个粒子进行并行资源分配,即在同一时隙内,针对同一信道状态,得到M种资源分配结果[7]。设资源分配结果集合为S,解的集合为X,迭代次数为t。采用随机调度方法分配资源,得到初始分配方案S=(s1,s2,…,sm,…,sM)T,sm为一种用户关联和子载波的分配方案,可表示为
(6)
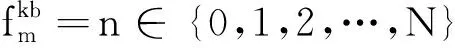
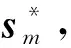
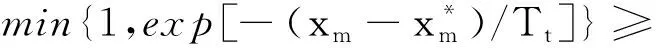
(7)

步骤1 产生初始分配方案sm,初始温度T0,依据初始分配方案sm得到目标函数的初始解xm。
步骤4 更新温度Tt=Tt-1×a。
步骤5 重复步骤2~步骤4,直到温度Tt<1,将输出的解作为最优解,结束程序。
2.2 功率分配
采用LM算法进行功率优化分配,通过调整用户的功率控制因子β,找到用户最优功率控制因子,减少用户间的干扰,进一步提升系统性能。将式(5)进行二阶泰勒公式展开,得到
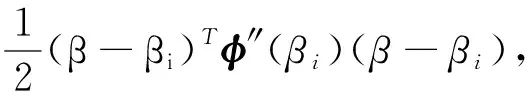
(8)
式中,φ′(βi)为Jacobian矩阵,φ″(βi)为Hessian矩阵,i为迭代次数。对式(8)两边同时求导,可得
βi+1=βi-φ″(βi)-1φ′(βi)。
(9)
在式(9)中添加阻尼因子μ,更新功率控制因子
βi+1=βi-ε(φ″(βi)-μI)-1φ′(βi),
(10)
其中,ε是迭代步长,I为单位矩阵。为了保证[φ″(βi)-μI]为负定矩阵,阻尼因子μ必须大于φ″(βi)的最大特征值。如果φ″(βi)的最大特征值小于0,那么μ=0。LM算法分配功率的具体步骤如下。
步骤1 将式(5)进行二阶泰勒公式展开,推导得到功率控制因子的迭代表达式。
步骤2 依照式(10)更新功率控制因子β。
步骤3 依据功率控制因子β以及式(1)和式(2)计算当前用户n的传输速率rnkb。
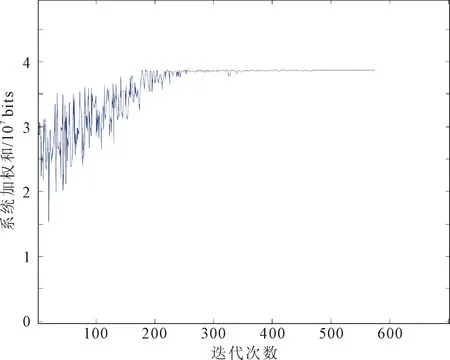
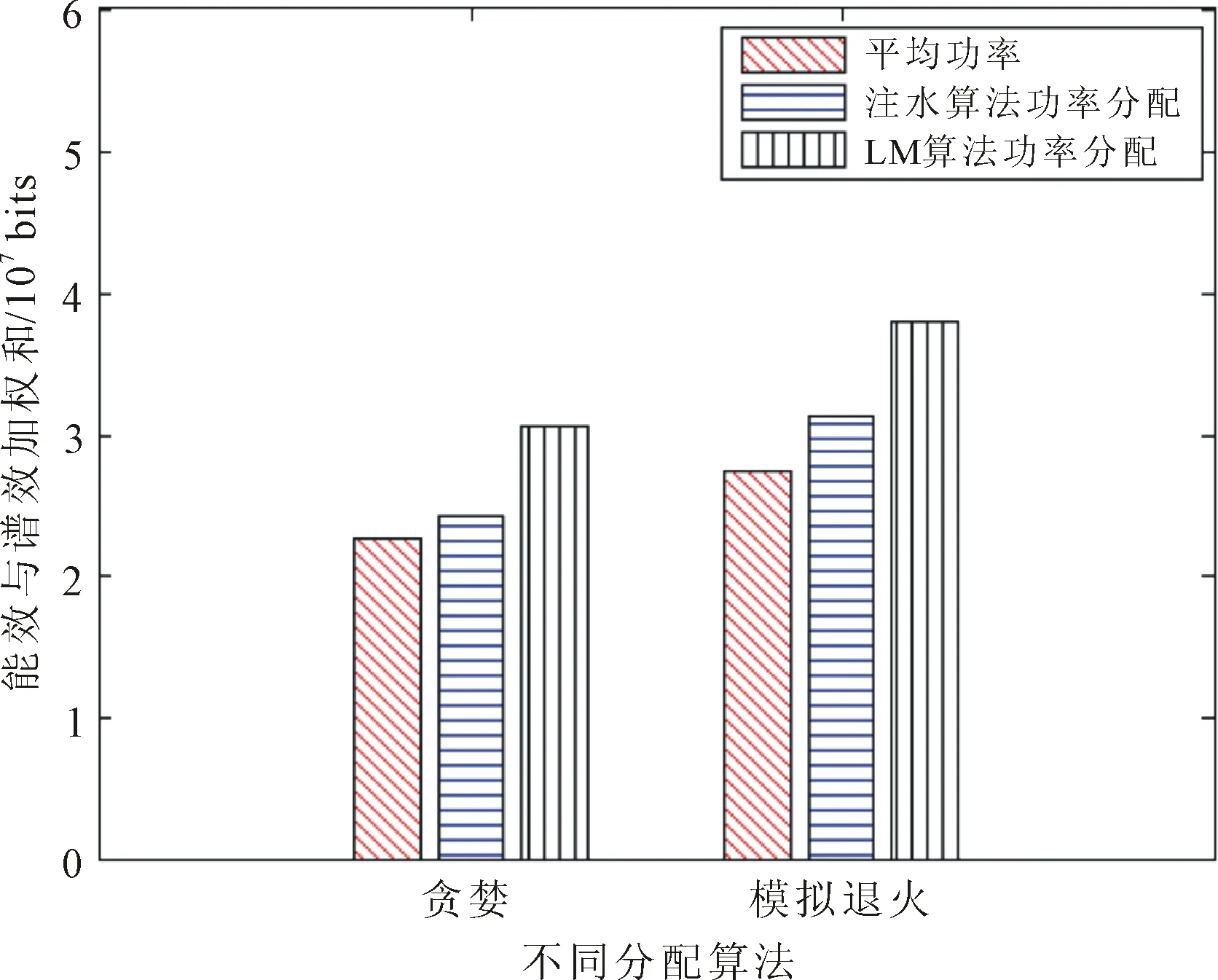
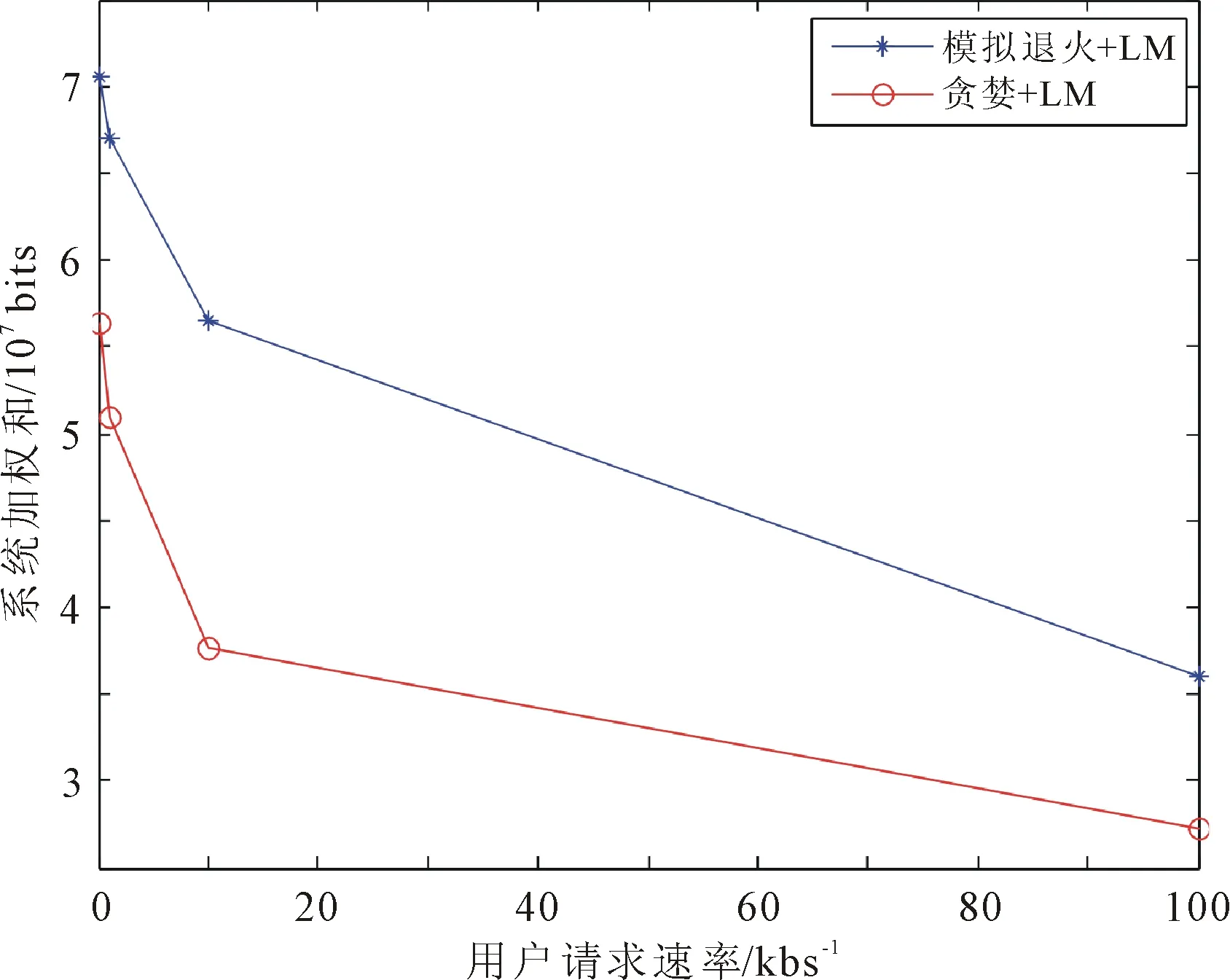
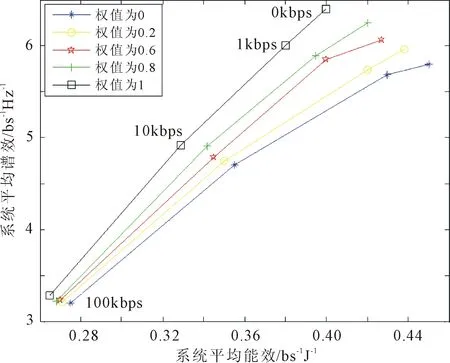
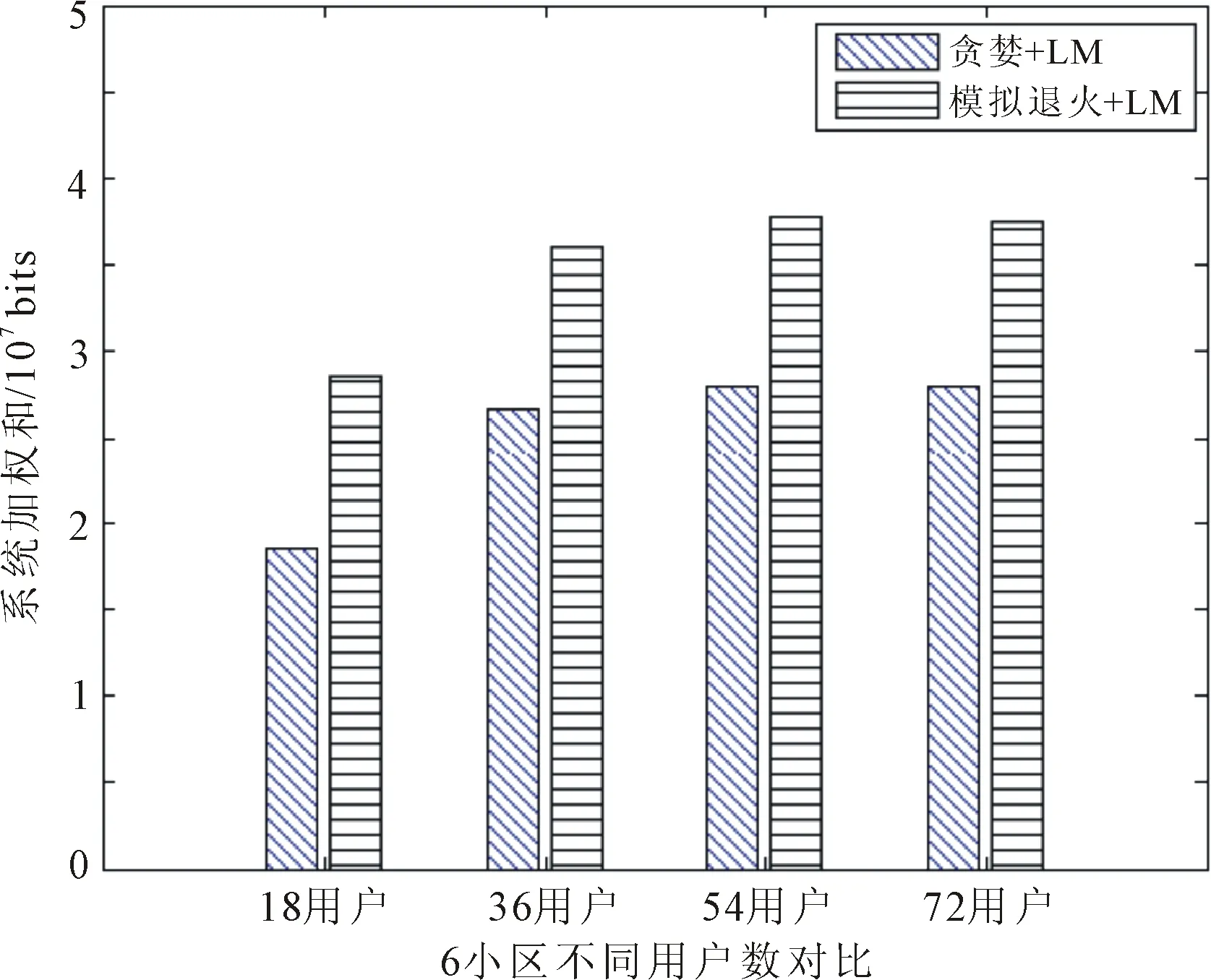
步骤4 若rnkb 采用城市微小区信道模型,设定参数载波带宽为10 MHz,子载波数量为12个,AP基站路径损耗为140.7+36.7 lgddB,阴影衰落为8 dB,AP基站发射功率为20 dBm。基于模拟退火联合LM分配方案对多维资源联合调度进行仿真,分析系统吞吐量加权和的变化,结果如图3所示。 图3 系统加权吞吐量随迭代次数的变化 由图3可以看出,随着迭代次数的增加,目标函数逐渐趋于稳定,达到收敛状态。 将能效与谱效加权和折算为系统的吞吐量,采用相同的功率分配策略,对比模拟退火算法与贪婪算法的性能差异;同时对比3种不同功率分配算法之间的性能差异,仿真结果如图4所示。 图4 贪婪与模拟退火算法仿真结果对比 由图4可以看出,采用相同的功率分配策略,模拟退火算法相比与贪婪算法对系统加权吞吐量的提升更为明显;在其他条件相同的情况下,LM功率分配对系统加权吞吐量的提升高于平均功率以及注水算法。 分别采用模拟退火算法联合LM方案与贪婪算法联合LM功率分配方案,对比分析不同用户速率需求下算法性能、不同权值下系统能效与谱效之间的耦合关系、以及同小区不同用户数量对系统加权和的影响,仿真结果分别如图5至图7所示。 图5 不同用户速率需求下算法性能对比 图6 不同权值下的系统性能对比 图7 同小区不同用户数对比 由图5可以看出,模拟退火算法联合LM方案优于贪婪算法联合LM方案。系统加权吞吐量随着用户请求速率的增加而减低,这是因为随着用户请求速率的提升,对资源块和信道质量的要求就更加苛刻,最终导致了系统性能逐渐减低。 从图6中可以看出,随着权值的增大,系统更偏向于谱效的提升;随着权值的减小,系统更偏向于能效的提升。并且经计算得出,8%谱效的下降使得能效提升10%左右。 图7可以看出,在小区数量不变的情况下,随着用户数的增加,模拟退火算法联合LM方案的系统加权吞吐量逐渐提升。随着用户数进一步增加,系统加权吞吐量逐渐趋于稳定。 结合上述仿真结果可以得出,模拟退火算法要优于贪婪算法,LM算法对系统权重吞吐量的提升要优于平均功率以及注水算法。实验同时表明了能效与谱效之间的耦合关系,在用户速率满足的情况下,注重能效的提升更利于资源的充分利用。 在超密集异构网络下,多维资源联合调度方案采用基于模拟退火以及LM算法,将用户关联、载波分配以及功率控制联合调度,在提高资源利用率的同时,通过分析系统能效与谱效之间的耦合关系,优化了多用户多维资源多种目标函数联合问题。仿真结果表明,模拟退火算法相比于贪婪算法而言,可以避免目标函数陷入局部最优陷阱,提升系统的加权吞吐量; LM算法相比于平均功率以及注水算法而言,可以有效的提升系统加权吞吐量,减少了用户间的干扰。该方案能够在超密集小区C/U分离结构下,进行多小区多维资源分配。3 仿真结果
4 结语
