一种参数自适应变化的强机动目标跟踪算法

潘静岩, 潘媚媚, 魏 勐, 李 靖

(1. 中国电子科技集团公司第二十七研究所 光电系统部， 河南 郑州 450047；2. 西安电子科技大学 综合业务网理论及关键技术国家重点实验室， 陕西 西安 710071)

强机动目标的精确跟踪在雷达技术中始终是一个难题，其最根本的原因在于目标的强机动使得跟踪建立的目标运动模型与目标实际动力学模型不匹配，导致跟踪滤波器发散，跟踪性能严重下降。

基于Singer模型的机动目标跟踪[1]，由于Singer模型对于机动加速度均值为零，其概率密度函数服从均匀分布的假设一般是不符合实际的，因此它只适用于匀速和匀加速范围内的目标运动。对于强机动目标跟踪来说，采用Singer模型会引起较大的模型误差。基于“当前”统计模型的机动目标跟踪，虽然“当前”统计模型在目标无机动或弱机动时有很好的跟踪性能，但在目标发生强机动的情况下，跟踪性能会显著下降[2-6]。基于Jerk模型的机动目标跟踪[7-8]，自适应跟踪算法是建立在卡尔曼滤波[9-10]基础之上，而卡尔曼跟踪滤波对强机动目标存在鲁棒性和跟踪精度低的问题。交互式多模型算法[11-13]同时采用多个运动模型逼近目标运动模型，虽然跟踪性能比单模型性能有所提高，但其跟踪精度受限于事先设计的多个模型与实际情况的匹配程度。此外，交互式多模型计算复杂，会影响高机动目标跟踪的实时性。因此，研究描述机动目标运动变化的改进模型和提高跟踪滤波器的性能是提高强机动目标跟踪性能的主要解决办法。

强跟踪滤波器利用正交性原理将时变渐消因子引入到预测协方差矩阵的修正中，提高了对突变机动目标的跟踪能力[14]。CS-Jerk模型借鉴了“当前”统计模型的思想，相对于Jerk模型能更好地匹配目标的实际情况[15]。STF-C-Jerk算法[16]将CS-Jerk模型与强跟踪滤波器相结合，在CS-Jerk模型的基础上，利用新息协方差矩阵的迹构造活化函数，可对机动频率和加速度变化率极大值进行自适应调整[17]。文献[18-19]对强跟踪滤波器中的预测协方差矩阵采用多重时变渐消因子进行修正，可分别对各个状态变量进行调整，但多重时变渐消因子的尺度调节系数是根据先验信息设置的，存在着无法自适应调整的不足；文献[20]根据“当前”统计模型中的噪声分布特性推导了一种机动频率自适应的方法，但仅对加速度维度上的机动频率以及加速度的极大值进行自适应调整，对于机动性很强的运动目标来说，跟踪精度会下降。

本文借鉴文献[19-20]，在文献[16]的基础上提出一种参数自适应变化的强机动目标跟踪算法。在CS-Jerk模型的基础上，对加速度变化率维度上的机动频率以及加速度变化率的极大值进行自适应调整；然后利用滤波残差信息对强跟踪滤波器中的多重时变渐消因子的尺度调节系数进行自适应调整，以期提高强机动目标的跟踪性能。

1 改进的CS-Jerk模型

1.1 CS-Jerk模型

Jerk模型[21]是在加速度模型基础上增加了一个维度，即实时地对高机动目标加速度的导数——加速度变化率进行估计，以此得到对目标状态更加精确的估计，从而达到对机动目标的跟踪目的。但是，当机动加速度为单位阶跃输入时，Jerk模型的稳态系统误差不趋于零[8]，产生这一现象的根本原因在于Jerk模型中关于目标加速度变化率为零均值随机过程的假设是不符合实际的。因此，CS-Jerk模型假设目标的加速度变化率是非零均值的时间相关随机过程[15]，即

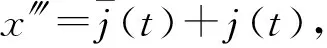
(1)

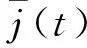
(2)

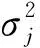
j′(t)=-αj(t)+w(t)，

(3)

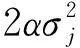
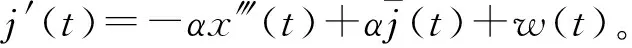
(4)

经过T周期采样、离散化后，k时刻的目标运动状态方程可表示为

(5)

以二维平面运动目标为例，状态向量可表示为X(k)=[x,x′,x″,x‴,y,y′,y″,y‴]T，其中x、y分别表示k时刻目标在X、Y方向上的位置；x′、y′分别表示k时刻目标在X、Y方向上的速度；x″、y″分别表示k时刻目标在X、Y方向上的加速度；x‴、y‴分别表示k时刻目标在X、Y方向上的加加速度。式(5)中的F(k)为状态转移矩阵，表达式为

(6)

其中

(7)

其余Fij(i=1,2;j=1,2;i≠j)均为四阶零矩阵。

G(k)为控制矩阵，表达式为

(8)

其中

(9)

其余Gij(i=1,2;j=1,2;i≠j)均为四阶零矩阵。

W(k)为过程噪声，是均值为0、协方差为Q(k)的高斯白噪声序列，且有

(10)

其中

(11)

结合式(5)，对目标进行观测的量测方程可表示为

Z(k+1)=H(k+1)X(k+1)+V(k+1),

(12)

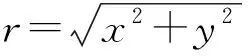
(13)

此时量测方程是非线性的。H(k+1)为量测矩阵，且有

(14)

V(k+1)为量测噪声，它是均值为0、协方差为R(k)的高斯白噪声序列，与过程噪声W(k)相互独立，且有

(15)

通过式(5)和式(12)对目标建立跟踪模型。基于CS-Jerk模型的卡尔曼滤波在稳态时动态误差为0[8]，说明CS-Jerk模型及其相应的自适应滤波算法在理论上具有较好地跟踪强机动目标的能力，但CS-Jerk模型中的机动频率和加速度变化率极大值无法进行自适应调节，需对其进行动态调整。

1.2 机动频率的动态调整

根据加速度与机动频率关系的推导方式[20]，令jm(t)=x‴(t)，则式(1)可表示为

(16)

对上式两边同时求导，可得

(17)

将式(17)带入式(3)得

(18)

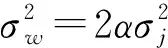
(19)

式中x服从正态分布，即x～N(0,1)。结合式(18)和式(19)可得

(20)

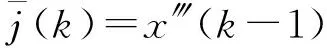
(21)

其中

(22)

1.3 加速度变化率极大值的动态调整

假设在k时刻滤波所得的距离函数[22]为

D(k)=vT(k)S-1(k)v(k),

其中，v(k)是k时刻的新息，S(k)是k时刻的新息协方差。D(k)服从量测维数的卡方分布，可以根据目标发生强机动的概率，查询卡方分布表得到机动判别门限M。当D(k)>M时，判定目标发生了机动，反之则判定目标未发生机动。若jmax 0为加速度变化率极大值的初始值，则调整加速度变化率极大值的表达式为

jmax=max(D(k)/M,1)jmax 0。

(23)

2 改进的强跟踪滤波器

2.1 强跟踪滤波器

强跟踪滤波器采用正交性原理，通过引入时变渐消因子，在线调整状态预测误差协方差矩阵，增大目标状态估计的补偿值，从而提高滤波器对状态变化的适应能力，对突变的机动目标仍能保持较好的跟踪性能[14]。STF算法采用时变渐消因子λ(k+1)对状态预测协方差矩阵进行修正，即

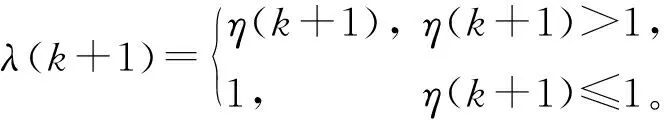
(24)

其中

(25)

N(k+1)=V0(k+1)-βR(k+1)-
H(k+1)Q(k)HT(k+1),
M(k+1)=H(k+1)F(k)P(k|k)FT(k)HT(k+1),

式中V0(k+1)是残差协方差矩阵，且有

(26)

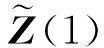
由式(24)可以看出，在状态误差中引入渐消因子λ(k+1)，根据残差自适应改善目标的状态估计，提高了滤波器的跟踪性能。此外，强跟踪滤波器在跟踪一般机动目标时，输出残差较小，使得λ(k+1)=1，此时算法退化为卡尔曼滤波器，保持了对一般机动目标的跟踪精度；在目标发生强机动时，强跟踪滤波器根据残差的变大而增大渐消因子，自适应地调节增益，增大了目标状态估计的补偿值，从而提高状态突变时的跟踪性能。

2.2 改进的强跟踪滤波器

对STF中的预测协方差矩阵采用多重时变渐消因子进行修正，但是该时变渐消因子尺度调节系数要根据先验信息获得，存在着不能自适应调整的缺点[17-18]。机动目标跟踪的理想状态是跟踪滤波值等于目标运动的真实状态值，即量测偏差等于量测值与滤波值之差，而实际跟踪中，滤波所得新息几乎不会与量测偏差相等。量测偏差可由雷达的跟踪精度获得，在雷达跟踪精度已知且目标运动状态平稳的情况下，滤波新息应该在量测偏差门限之内；目标一旦发生较大的机动就会导致新息超出量测偏差门限，新息越大说明机动性越大。基于上述思想，根据以下方法对时变渐消因子的尺度调节系数进行自适应调整。

假设多重渐消因子矩阵为

Λk=diag [λ1,k,λ2,k,…,λm,k],

λi,k对应k时刻第i个变量的渐消因子，且有[18]

(27)

(28)

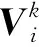
3 仿真及结果分析

为验证本文算法的有效性，设置一种强机动目标的运动轨迹，分别利用3种不同算法对目标运动轨迹进行跟踪，对比分析跟踪性能。

3.1 目标运动轨迹

目标的起始状态为[x,x′,y,y′]=[500,400,500,300]，对目标进行400 s的连续观测。1～70 s目标做匀速直线运动；71～140 s目标做角速度为2.2°的顺时针转弯运动；141～210 s目标做匀速直线运动；211～280 s目标做角速度为2.2°的逆时针转弯运动；281～350 s目标做匀速直线运动。图1是目标的运动轨迹图，图2是目标的速度变化图。

图1 目标运动轨迹

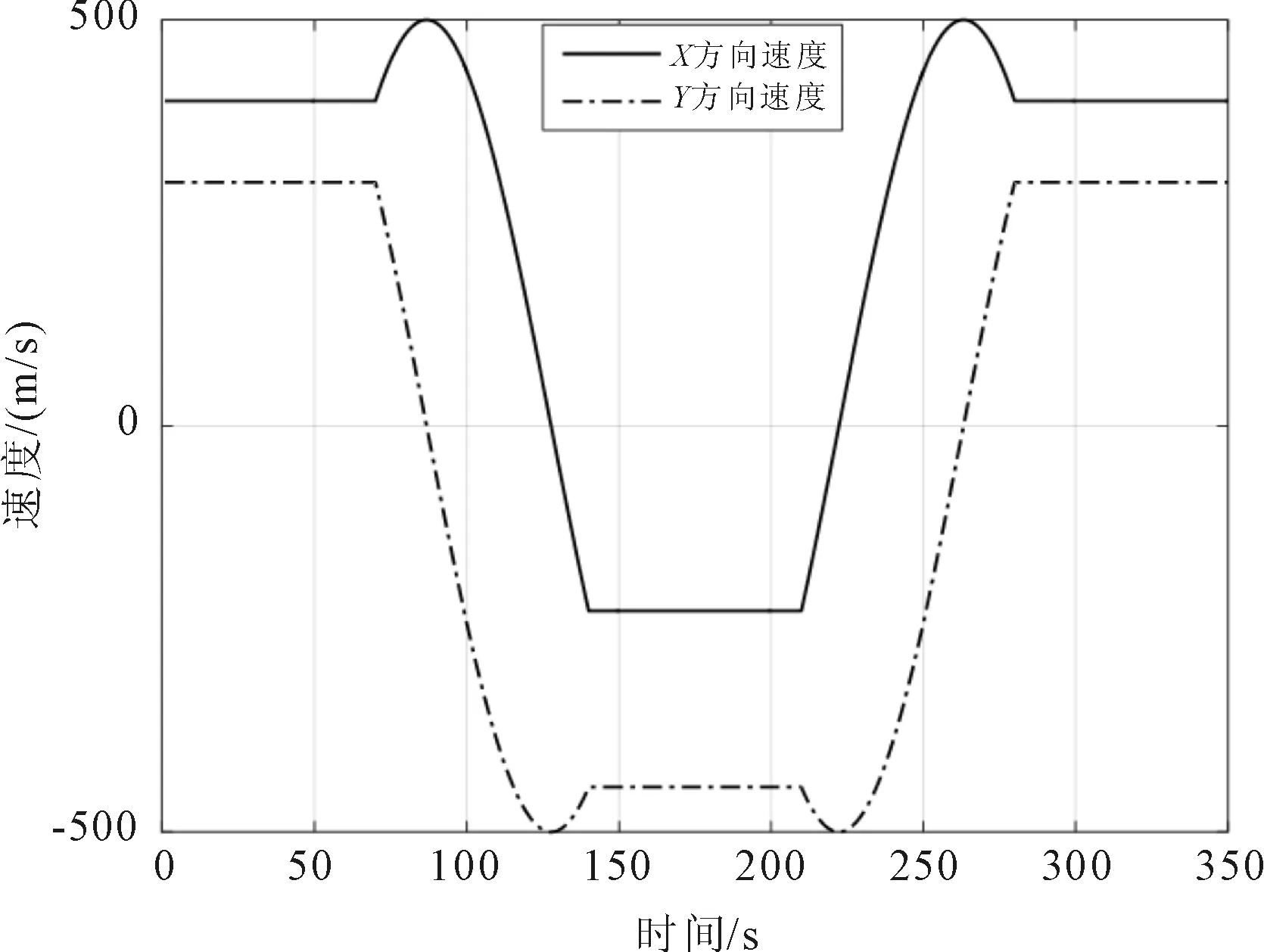
图2 目标速度变化

3.2 仿真设置

(1)跟踪参数设置

雷达的距离和方位角的标准差分别为σr=100 m和σθ=0.1°，雷达采样间隔为T=1 s。

(2)跟踪算法设置

算法1：文献[16]算法，机动频率为0.5，加速度变化率极大值设置为20 m/s3。

算法2：改进CS-Jerk跟踪模型+STF滤波算法(STF-AC-Jerk)算法，参数设置同算法1，M=7。

算法3：改进CS-Jerk模型+改进STF滤波算法，即本文算法，参数设置同算法2。

分别采用以上3种算法，对目标进行100次蒙特卡洛仿真跟踪。

(3)跟踪性能指标

采用X、Y方向以及距离的均方根误差( root mean square error ，RMSE)作为跟踪性能的衡量指标。

3.3 仿真结果分析

3种算法对目标进行跟踪所得的X、Y方向以及距离的均方根误差对比结果如图3所示。

(a) X方向RMSE

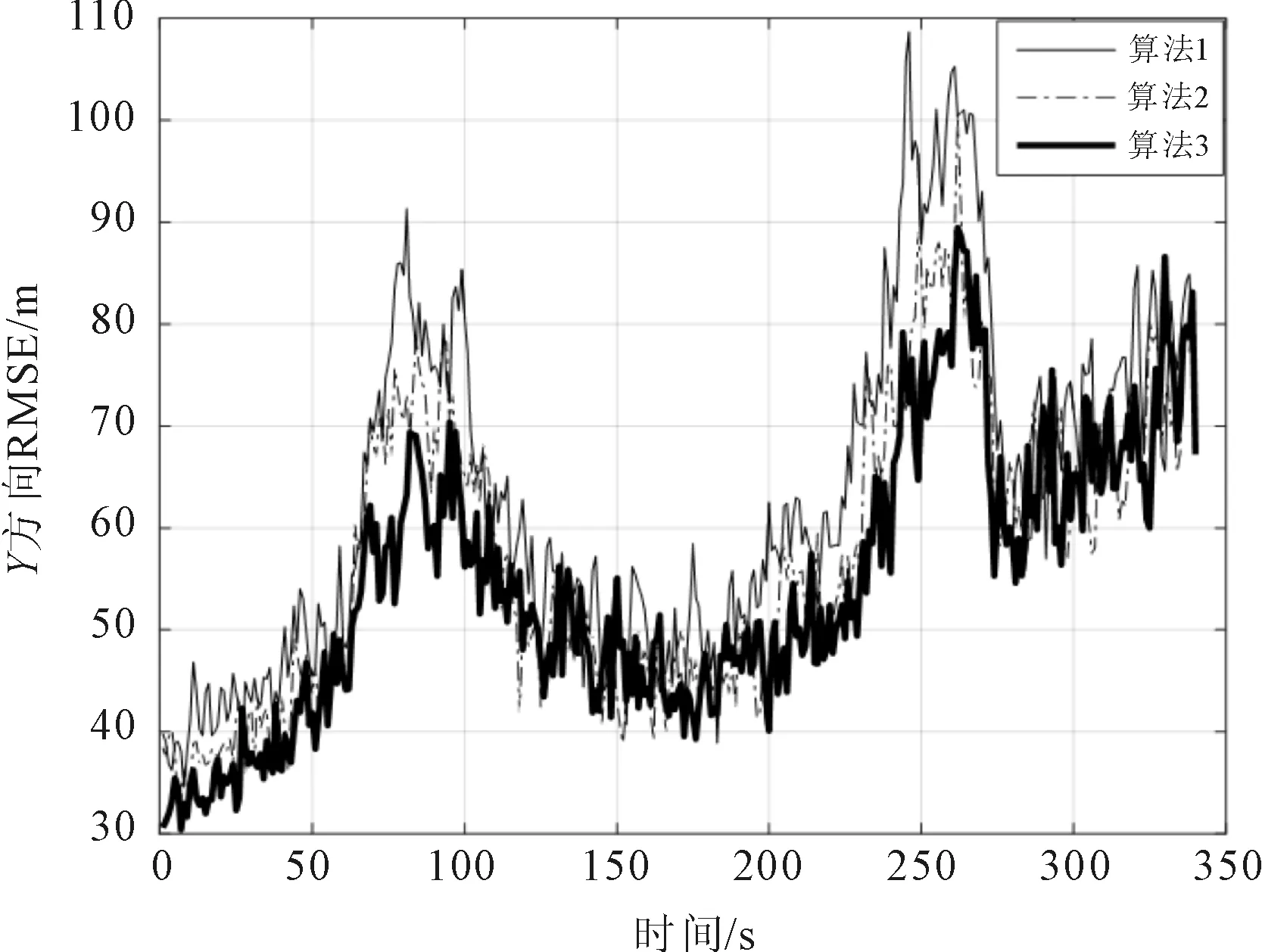
(b) Y方向RMSE

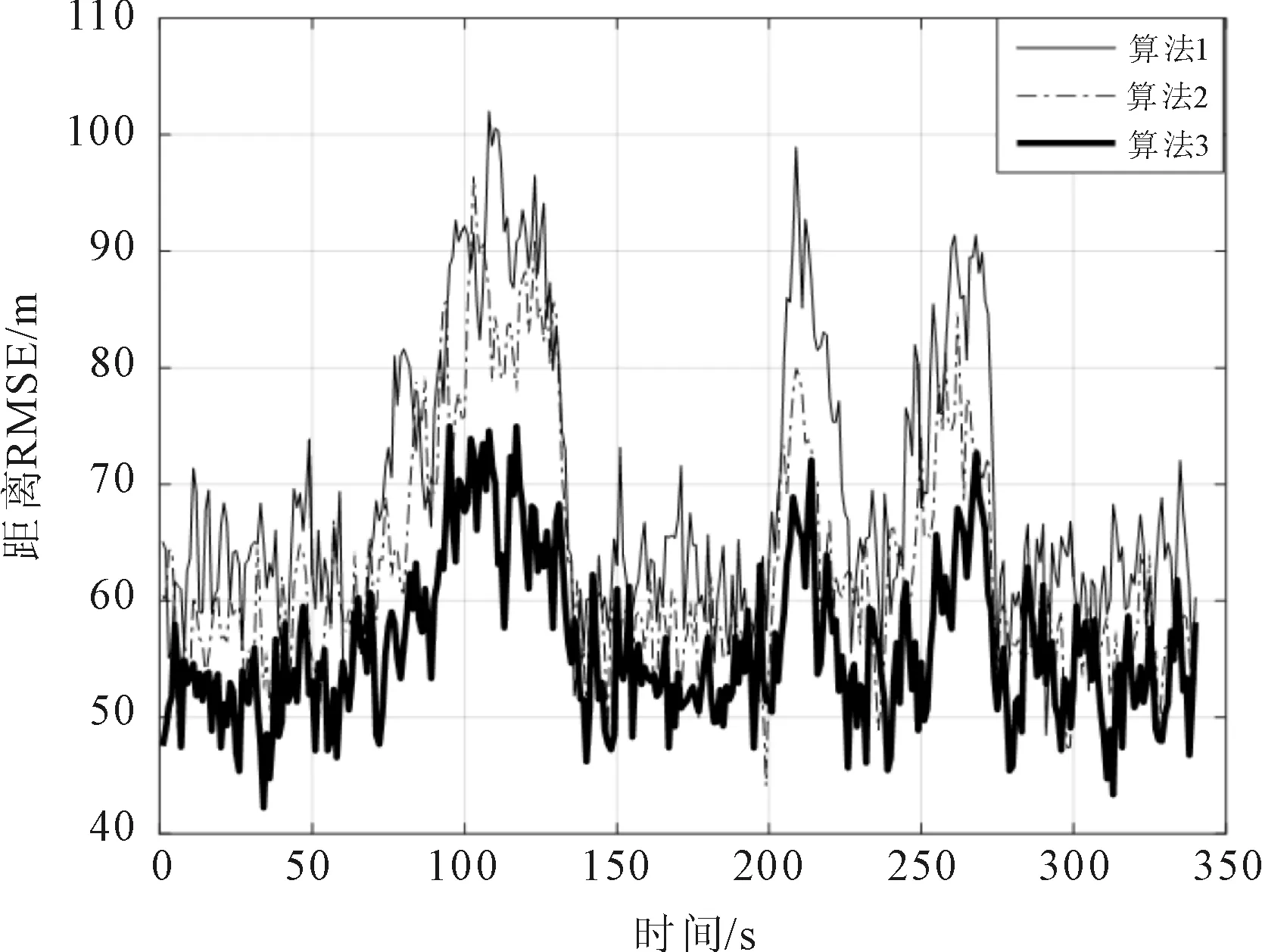
(c) 距离RMSE

由图3可以看出，算法3的跟踪均方根误差最低，跟踪性能最好，算法2次之。结合图2的X、Y方向速度变化，可以看出，在X方向上，90 s和210 s的时刻发生了强机动；在Y方向上，70 s和230 s的时刻发生了强机动，在距离上表现就是分别在70 s、90 s以及210 s和230 s的时候发生了强机动。在强机动阶段，3种算法的跟踪误差均明显增大，对比也更为明显；而在目标非机动阶段，3种算法的跟踪性能差别不是很大，但从整体上依然可以看出，算法3的跟踪性能最好，提高了目标的跟踪精度。3种算法的跟踪均方根误差均值对比如表1所示。

表1 3种算法跟踪的均方根误差均值对比

由表1可知，算法2相对于算法1，对目标跟踪的X、Y方向以及距离的均方根误差分别提高了8.014%、9.143%、8.822%，说明对CS-Jerk模型参数自适应的改进能更好地适应目标的机动变化。而算法3相对算法2，对目标跟踪的X、Y方向以及距离的均方根误差分别提高了7.830%、3.518%、9.963%，则说明对滤波器的改进提高了对目标跟踪的滤波精度。

因此，通过对CS-Jerk跟踪模型以及强跟踪器的改进，提高了强机动目标的跟踪精度，验证了本文算法的有效性。

4 结语

参数自适应变化的强机动目标跟踪算法根据CS-Jerk模型中的噪声分布特性，对机动频率进行自适应更新；根据滤波残差信息对加速度变化率的极大值进行自适应处理；最后又根据强机动目标新息特性改进了强跟踪滤波器，改善了目标跟踪建模难度大，跟踪滤波器易发散等问题。仿真结果表明，本文算法提高了对强机动目标的跟踪精度。