基于GKT-RT-GDP的长时间相参积累算法
2019-09-05谢锡海苏欣阳张依旋
谢锡海, 苏欣阳, 张依旋
(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
在飞机飞行过程中,需要实时测量飞机距地面的实际高度,测量的精度直接关系到乘客、飞行员以及飞机的安全。脉冲雷达高度表是一种通过测量电磁波往返时间来确定飞行器到地面垂直距离的机载无线电设备,是飞行器的重要仪表[1]之一。脉冲雷达高度表由发射、接收装置和显示器组成,发射机通过天线发射线性连续变化的调频波,接收机接收到的电波频率和发射机发射的电波频率之间的差值与接收到的电波所往返路径的时间成比例,这样便可通过差频求出飞机的飞行高度。
对回波信号的检测准确度是脉冲雷达高度表测量精度的关键,目前常采用长时间相参积累的方法来提高信号的可检测性[2-3]。由于飞机在飞行过程中会有匀速、加速等复杂的运动状态,会造成脉冲雷达高度表的脉冲回波信号产生多普勒频率徙动(Doppler frequency migration, DFM)和距离徙动(range migration, RM)。距离徙动包括距离走动(range walk,RW)和距离弯曲(range curvature,RC)。这些问题的存在使得传统的相参积累方法无法直接对回波信号进行有效的积累[4]。
对于RW的补偿和相参积累的计算,有两种经典算法即Keystone变换(Keystone transform, KT)[5-7]和拉东傅里叶变换[8-9]。KT方法通过尺度变换来进行距离走动的校正进而实现信号的相参积累[10]。拉东傅里叶变换通过在距离-速度域进行联合搜索以实现相参积累[11-12]。这两种算法在没有雷达高度表运动信息的情况下均可消除RW[13],但这两种算法只适用于匀速运动信号模型,不适用于匀加速运动信号模型。考虑加速度对回波信号造成的影响,基于广义拉东傅里叶变换的相参积累算法[14]通过对初始距离、速度、加速度进行搜索来实现相参积累,这种算法需要通过联合搜索目标的运动参数,运算复杂度较高且会出现盲速旁瓣,不利于对信号的检测;基于KT与广义去调频处理(generalized dechirp process, GDP)的相参积累算法使用GDP估计加速度信息,消除加速度对回波信号带来的影响,这种算法能有效地消除加速度带来的DFM现象[15],但没有考虑加速度较大时存在的距离弯曲现象。以上两种改进算法在一定程度上削弱了加速度带来的影响,但运算量较大,应用范围受到限制[13]。
为了减小雷达高度表回波信号在长时间相参积累期间受RM和DFM的影响,本文拟提出一种基于广义Keystone变换(generalized Keystone transform, GKT)、拉东变换(radon transform, RT)和GDP的长时间相参积累算法。使用GKT、RT对速度与加速度共同引起的RM进行校正,应用GDP对加速度进行估计进而削弱DFM现象,然后对回波信号做相参积累,以期提高雷达高度表对其回波信号的检测性能。
1 雷达高度表发射接收信号模型
1.1 发射信号模型
假设雷达高度表发射的信号为线性调频脉冲信号,在相参积累期间共发射M个脉冲信号,定义慢时间tm=(m-1)Tr为第m(m=1,2,…,M)个脉冲信号发射的初始时间,Tr为脉冲重复周期。定义快时间τ=t-tm为两次发射脉冲之间的时间,t为现实时间,则雷达高度表发射的第m个脉冲信号[4]可表示为
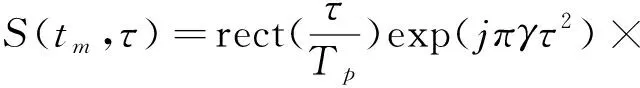
(1)
其中rect(·)为矩形函数,Tp是脉冲持续时间,j为虚数单位,γ和fc分别表示调频频率和载波频率。
1.2 回波信号模型
假设在相参积累期间,雷达高度表是朝向地面点目标做匀加速运动,且在一个脉冲重复周期内雷达高度表的高度不变,则雷达高度表与地面点目标之间的距离[11]可表示为
(2)
其中R0为初始距离,v为雷达高度表的径向速度,a表示径向加速度。由此,雷达高度表接收的第m个基带回波信号[4]可以表示为
(3)
其中Ain表示回波的复振幅,c表示光速,λ=c/fc为信号波长。接收到的回波信号经过脉冲压缩[4]后可表示为
(4)
其中A0表示脉冲压缩后振幅,B为信号带宽。
令ξ=f/fc,f为快时间频率。对式(4)做快时间τ的快速傅里叶变换可得第m个回波信号在快时间频域的形式[4]为
(5)
其中A1表示对快时间做快速傅里叶变换后的信号幅度。
当雷达高度表的运动速度比较高且脉冲重复频率较低时,雷达高度表会出现速度模糊现象,此时雷达高度表的速度[13]可以表示为
v=nkva+v0。
(6)
其中nk表示速度模糊数;va=λfr/2为模糊速度,fr表示脉冲重复频率;测量速度v0=mod(v,va)并满足|v0| 将式(6)代入式(5)后,第m个回波信号在快时间频域可表示为[13] (7) 雷达高度表回波信号慢时间一次项、二次项与快时间频率存在耦合关系,将分别带来RW和RC现象,且由于快时间频率与慢时间的二次项之间也存在耦合关系,回波信号会发生DFM现象[13]。 针对进行相参积累过程中雷达高度表回波信号出现的RC、RW和DFM现象,首先利用GKT对RC进行校正;其次,使用RT估计雷达高度表的速度信息,构造距离走动补偿函数完成对RW的校正;再次,应用GDP估计雷达高度表的加速度,进而构造二次相位补偿函数完成对DFM的校正;最后,对RM和DFM校正后得到的时域回波信号做慢时间的快速傅里叶变换,完成对回波信号的相参积累。基于GKT-RT-GDP的长时间相参积累算法的实现过程如图1所示。 图1 基于GKT-RT-GDP的长时间相参积累算法过程 (8) (9) (10) 将式(9)、(10)代入式(8)可得做GKT处理后回波信号的近似值 (11) 式中V=v0+2nkva。 对式(11)中信号的快时间频率f做傅里叶逆变换得GKT处理后信号的时域形式为 (12) 从式(12)中可以看出,雷达高度表各个回波信号的峰值出现在同一距离单元,此时由加速度引起的RC可以通过GKT消除,因此,雷达高度表的运动轨迹可以看作是沿ta方向的斜直线。 通过RT来估计直线的斜率,进而可以对雷达高度表的速度信息做出估计。基于RT的雷达高度表轨迹斜率估计原理[13]如图2所示。直线L表示经GKT处理过后雷达高度表的轨迹,(ρ0,θ0)是RT对直线L的处理结果,直线L的斜率[13]为 (13) 图2 基于RT的雷达高度表轨迹斜率估计原理 (14) 距离徙动校正后的时域回波信号为 (15) 从式(15)可以看出,RW已经得到补偿,即经过GKT和RT处理后由雷达高度表的速度和加速度引起的RM得到校正,然而由最后一个指数项可知,DFM现象依然存在,为得到较好的积累增益,仍需要对DFM做相位补偿处理。 从式(15)可知,回波信号Srw(ta,τ)的相位是一个带有平方项的信号,通过GDP来估计雷达高度表的加速度,现将相位补偿函数Gb(ta)表示为 (16) 其中b为加速度的预估计值。 将式(15)与式(16)等号右边相乘,得到回波信号的相位补偿形式为 (17) 从式(17)可以看出,当b=a时,信号就是一个正弦信号并且各个脉冲信号都被矫正到了同一个距离单元上,即τ=2R0/c。则加速度a的估计值可以表示为 (18) 其中FT(·)表示对慢时间ta的傅里叶变换。 由加速度的估计值可以重新构建相位补偿函数 (19) (20) 在经过GKT-RT-GDP的三步处理后,消除了雷达高度表回波信号的RM和DFM现象,保证了雷达高度表各个回波信号的相参性,从而可计算雷达高度表回波的相参积累。 对式(20)中Srw(ta,τ)的慢时间ta做快速傅里叶变换,得到雷达高度表各个回波信号的相参积累结果 (21) 其中A3表示相参积累后信号的幅度,Tc=NTr表示信号观测的总时间。由式(21)可以看出,雷达高度表的回波能量在同一距离单元内完成了相参积累。 使用matlab对实现算法进行仿真,设置雷达高度表回波信号的载波频率fc=10 GHz,信号带宽B=150 MHz,采样频率fs=300 MHz,脉冲持续时间Tp=20 μs,脉冲重复频率fr=2 000 Hz,相参积累的脉冲数M=201。 设置雷达高度表的初始速度v=100 m/s,径向加速度a=400 m/s2,并假设雷达高度表离地面的初始距离为R0=3 000 m。 由仿真设置参数可计算出距离单元为1 m,相参积累总时间为0.1 s,雷达高度表在长时间相参积累期间走动的距离为12 m[4],即走动了12个距离单元,其中因为速度走动了10个距离单元,因加速度走动了2个距离单元。 回波信号经过脉冲压缩后的仿真结果如图3所示。图3(a)为脉冲回波信号的距离走动图,图中分别在第3 001、2 996和2 995、2 989个距离单元,出现了第1、101、201个脉冲回波信号,即相参积累期间总共跨越了12个距离单元。图3(b)是各个脉冲回波信号的等高图,表示雷达高度表的高度轨迹。受速度和加速度共同作用产生的影响,从仿真结果可以看出此时的轨迹是一条弯曲幅度较小的曲线。 经过GKT方法对距离弯曲校正后的结果,如图4所示。图4(a)为距离弯曲校正后的距离走动图。可以看出,此时第1、101、201个脉冲回波信号分别位于第3 001、2 996、2 991个距离单元,脉冲回波信号仍跨越10个距离单元。图4(b)为距离弯曲校正后的回波信号等高图,此时的轨迹是一条直线,由加速度造成的距离弯曲已经被校正,只存在线性距离走动。 经过RT对雷达高度表速度进行估计并构造补偿函数来校正线性距离走动的仿真结果,如图5所示。从图5(a)仿真结果可以看出,各个脉冲回波信号已经被校正到了同一距离单元内,即此时回波信号的距离徙动现象已经被消除。从图5(b)的仿真结果可以看出此时各脉冲回波信号均位于同一高度,不在受距离徙动的影响。 图3 脉冲压缩后的仿真结果 图4 距离弯曲校正仿真结果 图5 距离走动校正仿真结果 通过GKT和RT处理能对距离弯曲和距离走动的进行校正,但是还未对DFM进行校正。在相参积累时,回波信号的能量会分散在不同的多普勒频率单元上,依然会对相参积累的效果造成影响。进一步使用GDP算法校正DFM。 基于GDP算法对径向加速度值进行搜索,仿真结果如图6所示。可以看出,峰值出现在a=400 m/s2处,实验结果表明了对径向加速度值进行估计的正确性。 图6 基于GDP的径向加速度估计仿真 使用估计出的径向加速度值构造补偿函数对多普勒徙动进行相位补偿前后的积累结果,如图7所示。通过对图7(a)与图7(b)仿真结果进行比较可以看出,在相位补偿前,回波信号能量分散在多个多普勒频率单元,而相位补偿后的积累集中在一个多普勒频率单元内,且相位补偿后的积累幅度要比相位补偿前的积累幅度高出约170个单位。 图7 多普勒相位补偿前、后的积累结果 将本文算法与基于KT-GDP的相参积累方法进行比较。 假设在相参积累期间内,雷达高度表积累的脉冲数为M,距离单元个数为L,径向加速度的搜索个数为Na,极坐标角度搜索数为Nθ,极坐标半径的搜索个数为Nρ。分析两种长时间相参积累算法的处理过程可知,KT-GDP算法的运算复杂度为 LMlog2M+L2M+NaLMlog2M, GKT-RT-GDP算法的运算复杂度为 LMlog2M+L2M+NaLMlog2M+NθNρ。 可见本文算法比基于KT-GDP的长时间相参积累算法运算复杂度高出NθNρ。令极坐标的搜索数Nθ为90,极坐标半径的搜索数Nρ=L。两种算法在相同背景下运算复杂度随脉冲数的变化趋势,如图8所示。可以看出,在相同的仿真条件下,两种算法运算复杂度的差异可以忽略。 图8 两种算法的复杂度 在相同的仿真设置条件下,基于KT-GDP算法和所提算法的长时间相参积累结果,分别如图9和图10所示。可以看出,本文算法的相参积累后信噪比较基于KT-GDP的长时间相参积累高出5 dB,即相同的条件下,本文所提出算法的积累效果要优于基于KT-GDP算法。 图9 基于Keystone变换与GDP的相参积累 图10 基于GKT-RT-GDP的相参积累 因此,本文算法与基于KT-GDP的长时间相参积累算法相比,在运算复杂度增加不明显的前提下,可以比较准确地校正雷达高度表回波信号的距离弯曲现象,提升了相参积累的效果。 针对雷达高度表运动状态造成的距离徙动和多普勒频率徙动等现象,提出基于GKT-RT-GDP的长时间相参积累算法。依次使用GKT、RT、GDP完成对距离弯曲、距离走动、多普勒频率徙动的校正。通过仿真验证了算法对距离徙动和多普勒频率徙动的校正效果,并与基于KT-GDP算法相比,本文算法能相对有效地校正距离徙动和多普勒频率徙动,获得较好的相参积累效果。2 基于GKT-RT-GDP的长时间相参积累
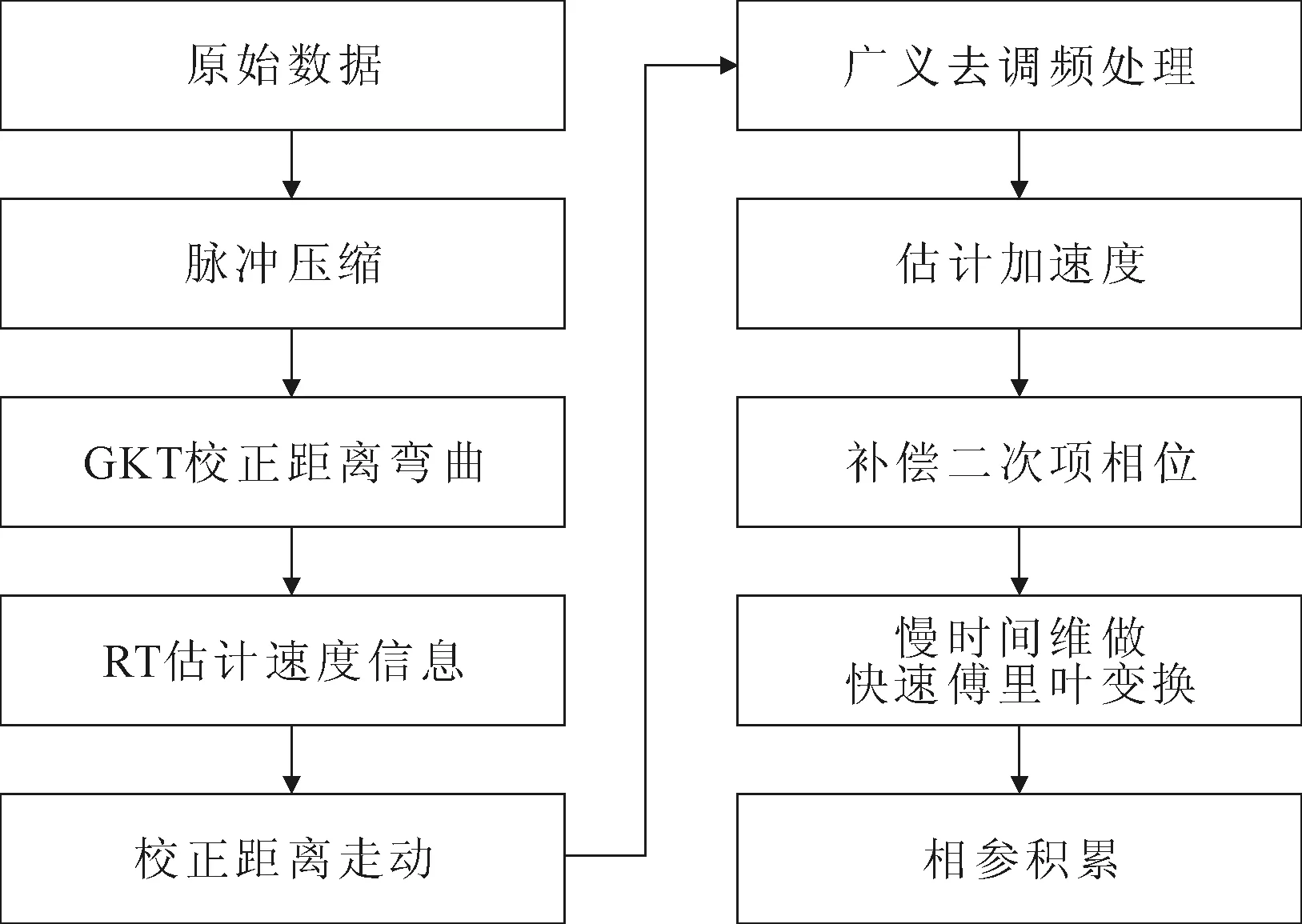
2.1 基于GKT的RC校正
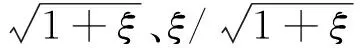
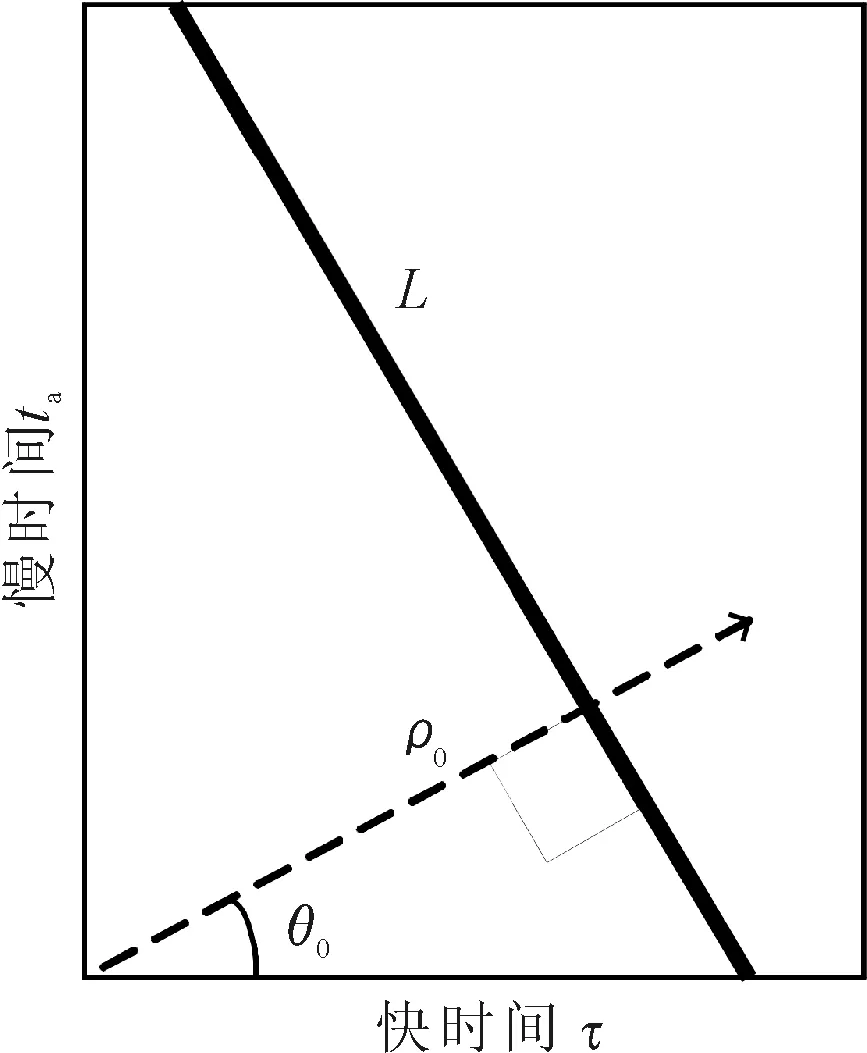
2.2 基于RT的RW校正
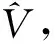
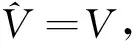
2.3 基于GDP的DFM补偿
2.4 相参积累
3 仿真结果及分析
3.1 实验条件
3.2 校正RM
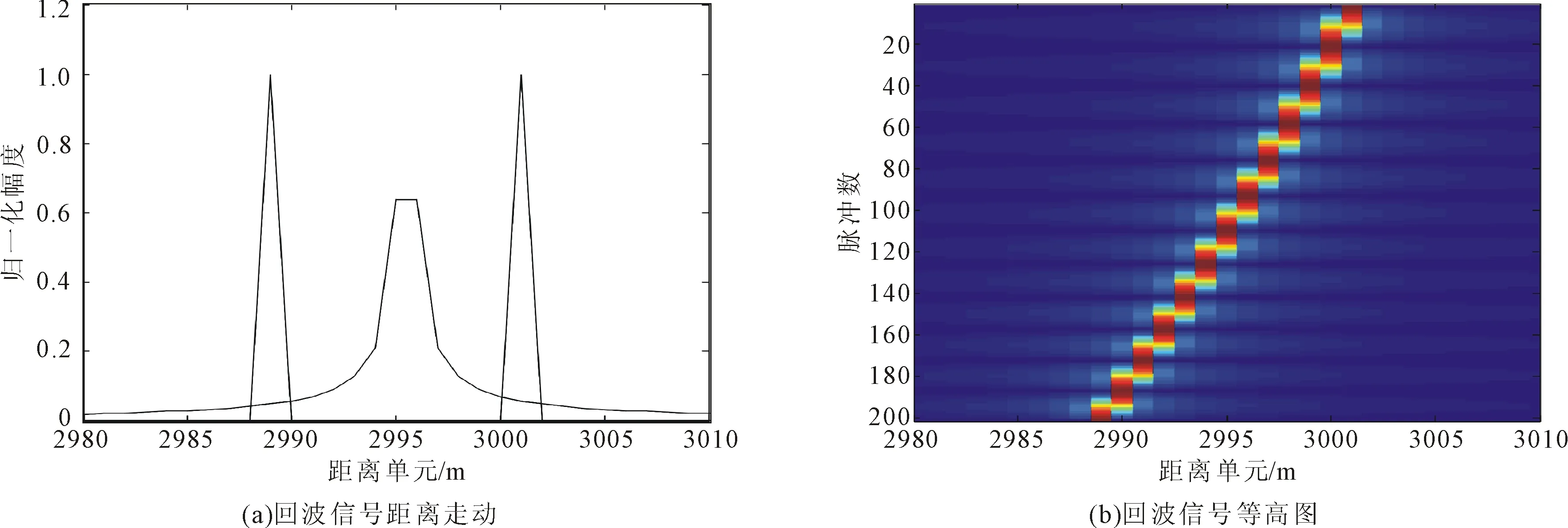
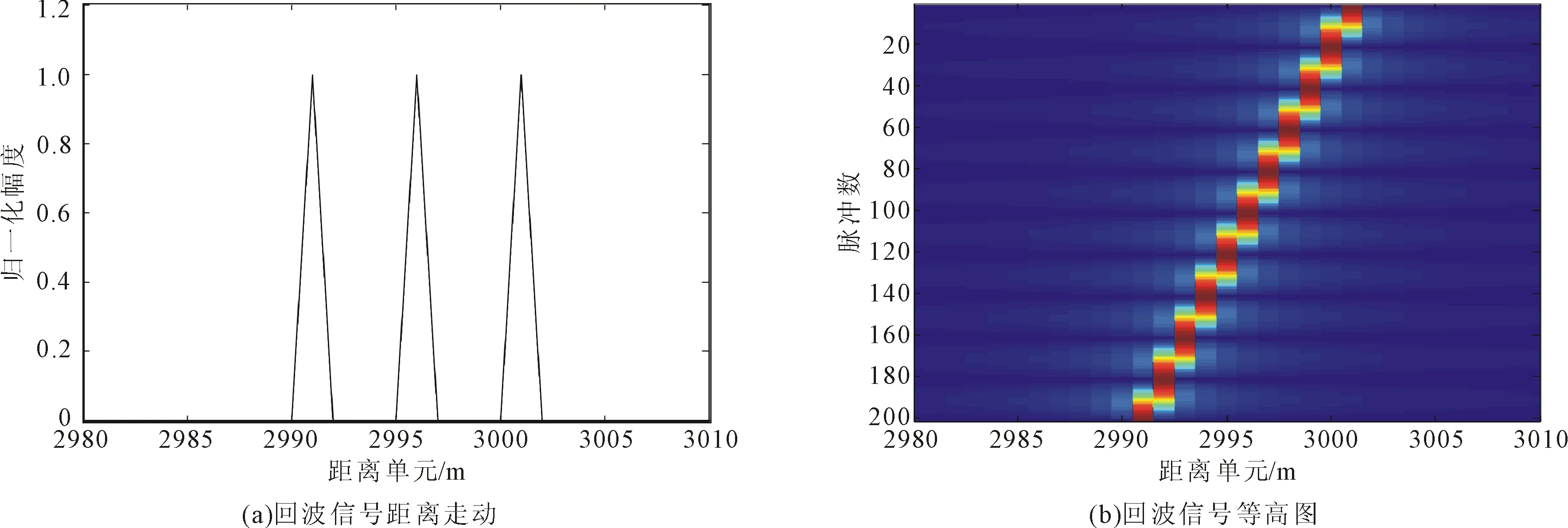
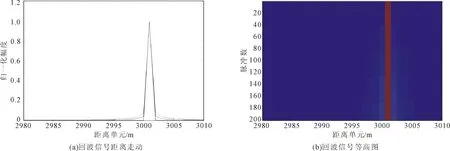
3.3 校正DFM
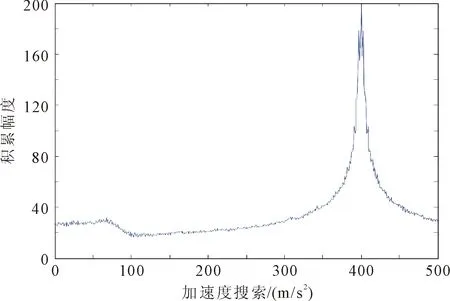
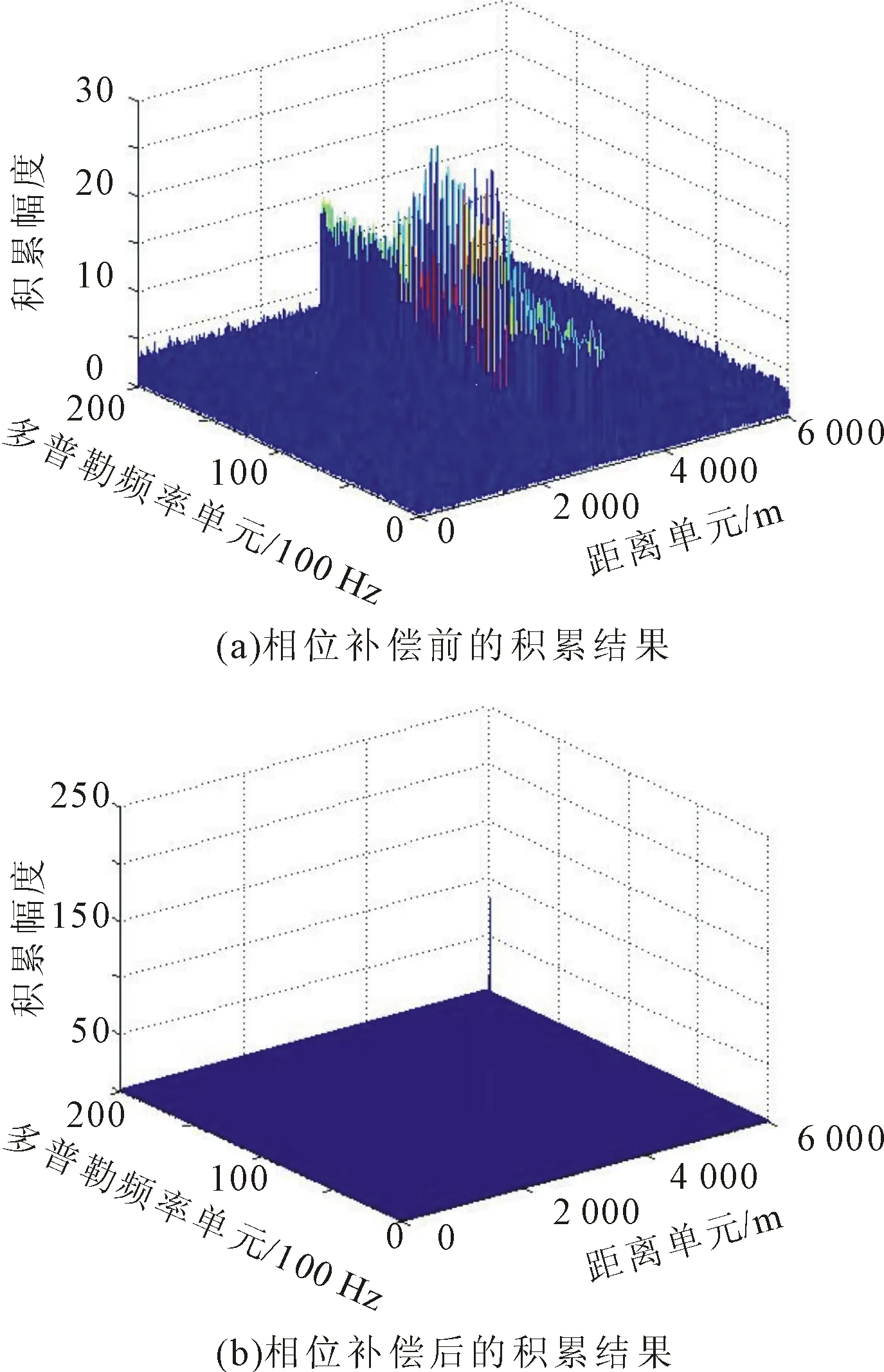
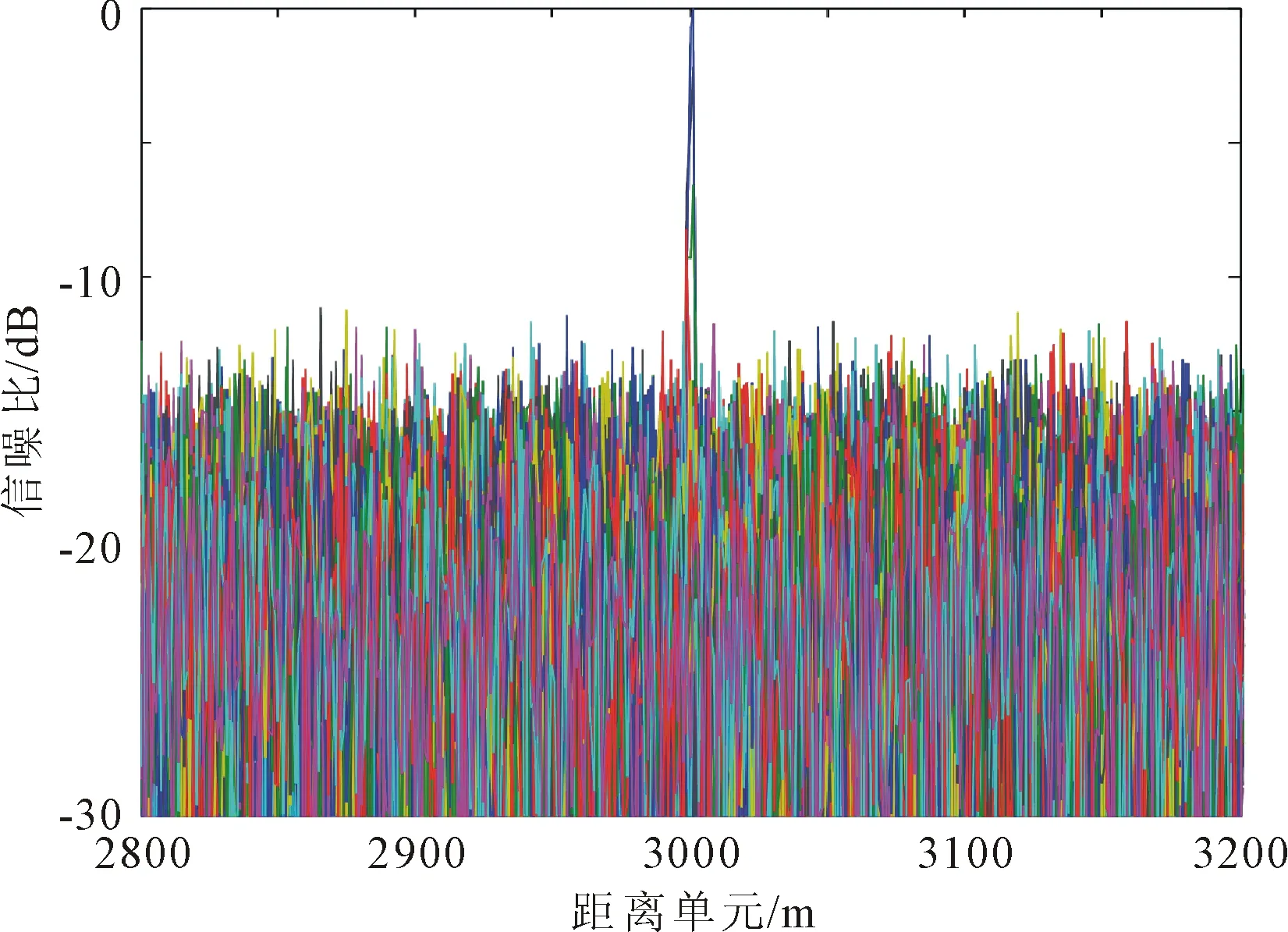
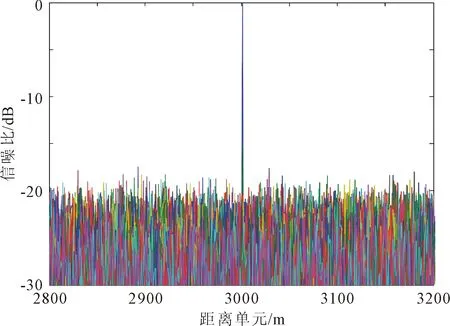
3.4 算法比较
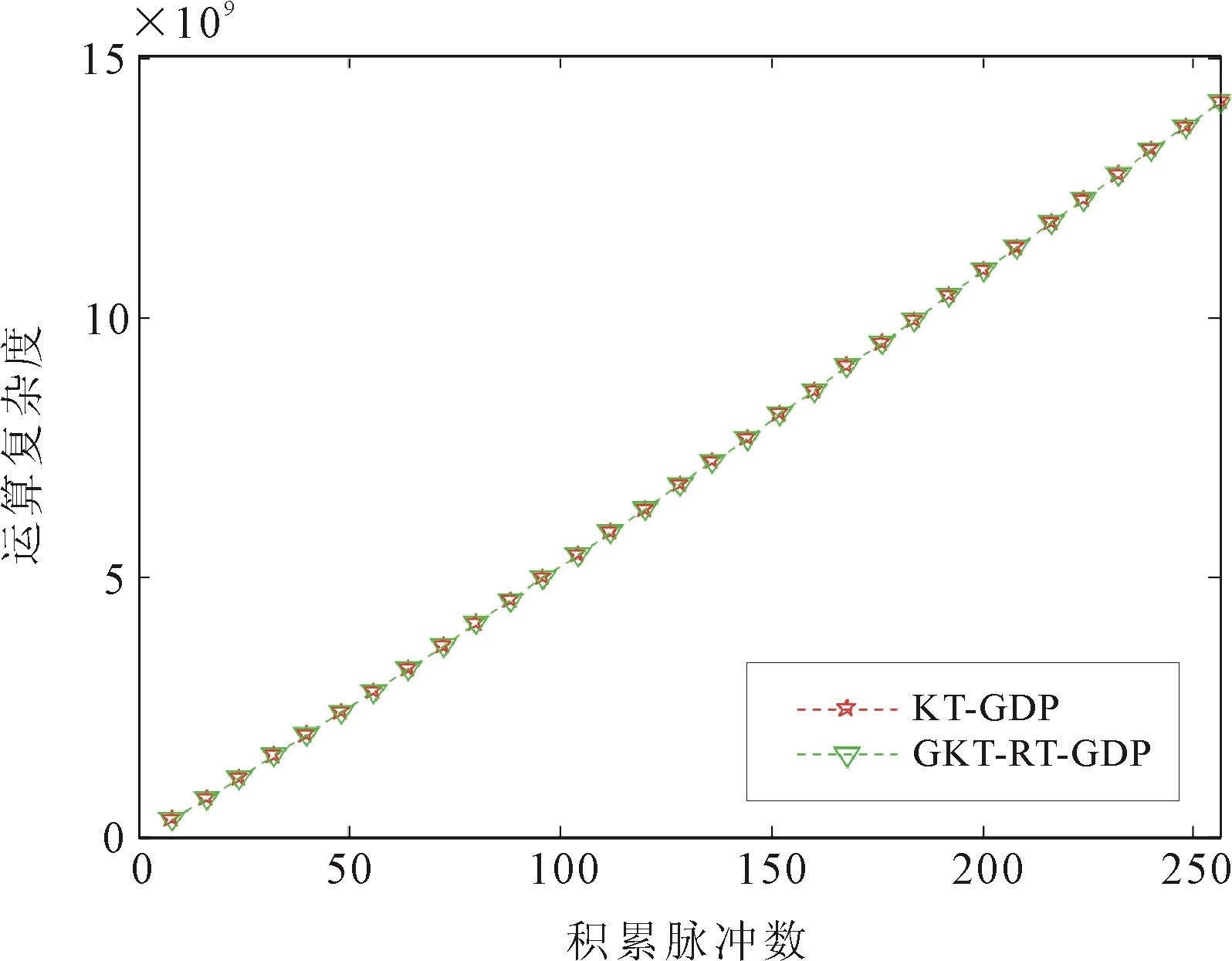
4 结语
