功放预失真系统中环路时延的频域估计

张 博, 淮一博, 任继军

(1.西安邮电大学 电子工程学院， 陕西 西安 710121； 2.西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

随着通信技术快速发展，带来了大量数字业务，而通信频谱资源显得越来越紧张，改进信号的调制方式是提高频谱利用率一种有效手段。一般情况下，常用调制方式有多进制正交幅度调制(multiple quadrature amplitude modulation，MAQM)、正交频分复用(orthogonal frequency division multiplexing, OFDM)等[1]技术，但MAQM和OFDM技术的峰均比(peak to average power ratio, PAPR)较高，制约了发射机中核心器件功率放大器(power amplifier，PA)的输出功率和效率[2]。应用数字预失真(digital pre-distortion, DPD)技术处理基带信号，能减弱发射器中PA非线性效应带来的不利影响[3]。DPD技术其编程灵活、适应能力强，成为了当前主流的PA线性化技术[4]。DPD技术对经过PA前的数据进行数字整形以达到扩展PA的线性范围的目的，其需要根据采样数据在基带进行系数辨识[5]。当数据经过模拟器件时会引起时延，如果时延未被校准，则导致DPD系数的辨识误差，从而恶化DPD对PA的线性化性能[4]。

为了满足预失真系统对时延估计的高精度要求，时延估计算法的计算复杂度较高。如利用互相关和插值理论[6-7]计算时延，一方面，该算法通过内插互相关函数的方法计算分数倍时延，虽然有较高的分辨率，但增加了算法的计算复杂度；另一方面，由于其需进行滤波处理，算法的处理过程相对复杂[4]。应用拉格朗日插值器估计分数倍时延的方法[8]，其运算量过大[9]。使用快速傅立叶变换进行循环卷积的方法[10]，通过抛物线曲线拟合来确定分数倍时延，但运算量过高[11]。还有通过四阶互相关函数来估计时延方法[12]，增加了时延的估计时长[1]。

为了降低时延估计算法的复杂度，提升时延估计的效率，本文拟提出一种频域时延估计算法，该算法直接提取频域相位差，同时采用快速傅里叶变换以期提高运算速度。使用前向数据与反向数据傅里叶变换之间的互相关最大化方法来估计整数时延，利用频域信号相位差来估计分数倍时延则，试图在保证精度前提下提高时延的估计速度。

1 数字预失真系统中的环路时延

PA的非线性特性会造成带内调制误差以及带外频谱扩展，而DPD技术可以有效地消除无线发射器中PA带来的不良影响。配置DPD前需先对环路时延进行估计，数字预失真系统的环路延迟估计原理示意图如图1所示。

图1 数字预失真环路延迟估计原理示意

图1中，x(n)表示第n个样本的基带输入信号，y(n)表示经过PA耦合衰减得到的反馈基带信号，z(n)表示第n个样本的预失真信号，τ0表示估计得到的环路时延，xalign(n)表示第n个样本的前向时延校正信号，G为PA增益。

为了提高PA的线性度与效率，DPD技术需要通过前向数据与反向数据建立PA的后逆模型[13]进行预失真系数的辨识，但是模拟链路带来的环路时延会影响系数辨识过程。为了消除时延对DPD的干扰，首先由x(n)与y(n)估计环路时延τ0，并得到第n个样本的校正信号xalign(n)，其次应用xalign(n)与y(n)建立后逆模型辨识预失真系数，最后将所得系数复制于预失真器中，从而建立环路对PA非线性校正的数字预失真功能。

传统时延估计通过时域互相关法函数式来进行，时延变量的互相关函数表达式[6]为

(1)

其中[·]*为求共轭，N为插值后总的采样点个数。|RXY(τ)|序列最大值所对应的τ即为环路时延，X(n)为x(n)的插值序列，Y(n)为y(n)的插值序列。

为了说明插值算法估计分数倍时延的原理，以插值算法常用的sinc函数方法[14]为例进行说明。sinc插值后的序列X(n)、Y(n)与sinc函数表达式[15]分别为

其中，Fs为采样频率；采样点m=1,2,…,M，M为基带输入输出信号总的采样点个数；TSI为采样间隔。

2 频域相位差时延估计及预失真

时延估计通常分为分数倍环路时延估计和整数倍环路时延估计两种。本文应用频域预失真环路的时延估计方法[16-18]，使用基于圆周相关的傅里叶变换算法估计整数倍时延，并完成整数倍时延校正。

分数倍环路时延则采用前向信号与反向信号的频域相位差来进行估计。为了提高估计精度，在相位作差过程中，结合最小二乘法获取估计的全局最优解，完成分数倍时延校正。

最后通过校正信号建立的后逆模型辨识预失真系数，从而产生预失真信号，并观察估计结果对于DPD线性化性能的影响。

2.1 整数倍时延估计

DPD系统的整数倍环路时延会引起线性化性能的恶化，因此需对其准确估计与校正。

令环路时延为τ0，τ0由整数倍时延τ1与分数倍时延τf组成。在功率对齐条件下，x(n)与y(n)间的关系[19]可以表示为

y(n)=x(n-τ0)+d(n)。

其中d(n)表示第n个样本的非线性失真信号。

令d(n)=0，则输入信号与反馈信号之间的关系为

y(n)=x(n-τ0)。

线性相移估计范围为2π，为了得到整数倍偏移量τi并进行校正，需要先计算互相关函数R(n)的峰值，计算公式[18]为

R(n)=IFFT[X(ω)(Y(ω))*]。

(2)

其中，ω表示信号频率，X(ω)与Y(ω)分别表示x(n)、y(n)的傅里叶变换结果，IFFT(·)表示快速傅里叶逆变换(inverse fast Fourier transform, IFFT)。

令max(R)=R(τi)，则第n个样本的整数校正输入信号xa(n)为

xa(n)=x(n-τi)。

此时，xa(n)与y(n)的关系为

y(n)=xa(n-τf)。

(3)

2.2 分数倍时延估计

即使完成了整数倍时延校正，分数倍时延τf的存在依旧会影响预失真系数的辨识，无法满足DPD系统对于估计时延的高分辨率要求，所以需要对分数倍时延进行估计与校正。

对式(3)中的xa(n)与y(n)时域信号分别作快速傅里叶变换(fast Fourier transform, FFT)得到

Y(ω)=Xa(ω)e-jωτf。

(4)

Y(ω)与Xa(ω)可分别表示为

Y(ω)=|Y(ω)|ejφy(ω),

(5)

Xa(ω)=|Xa(ω)|ejφxa(ω)。

(6)

其中φy(ω)、φxa(ω)分别为Y(ω)与Xa(ω)的相位。

由于PA会放大输入信号功率，导致前向与反向数据功率并不一致，影响预失真系数的辨识。在时延估计过程中，若xa(n)与y(n)已经过增益校正，则|Y(ω)|=|Xa(ω)|。

将式(5)与式(6)代入式(4)得

根据式(4)，Y(ω)与Xa(ω)复数比值的相位φ=-jωτf仅随ω线性变化，其对ω的导数是一个只取决于时延的常量，分数倍环路时延可表示[20]为

为了抑制PA相位失真对时延估计的影响，采用最小二乘法[21](least squares, LS)计算分数倍时延τf，计算公式为

τf=(ωTω)-1ωTφ。

(7)

其中，ω是以信号y(n)的带宽范围内频域相位φy(ω)为参考的归一化频率矩阵；φ是根据ω中的归一化频率分量确定的前向信号与反向信号间的相位差矩阵，此矩阵中每一个元素均在[-π,π]区间。

完成对分数倍时延的校准后，第n个样本的校正信号为

xalign(n)=IFFT[Xa(ω)e-jωτf]。

则y(n)与校正信号xalign(n)的关系为

y(n)=xalign(n)+d(n)。

2.3 预失真处理

经过整数与分数倍的两步时延估计与校正后，实现了前向数据与反向数据的同步。此时可进一步进行DPD系数辨识及基带输入信号的预失真处理。

采用广义记忆多项式(generalized memory polynomial, GMP)模型[22]，校正信号可表示为

其中，q与l表示记忆深度，q=0,1,…,Q-1；l=0,1,…,L-1;k表示非线性阶数，k=1,2,…,K；ak,q,l表示不同记忆深度与非线性阶数下的模型系数。

由最小二乘法得到的预失真待估计复系数矢量A的解析解为

A=[UHU]UHXalign，

其中

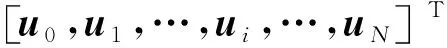
式中，Xalign为经时延校正的输入复信号矢量，U为复数核矩阵N为采样点个数。则预失真信号z(n)为

通过环路时延校正处理与预失真处理后，为了检验所提方法对于时延的估计准确度，应将预失真信号发送至PA，观测PA输出信号的ACPR校正效果。

3 实验结果及分析

3.1 测试环境

实验测试环境如图2所示。矢量信号发生器、频谱分析仪选用罗德与施瓦茨公司的SMW200A和FSW，待测PA选用LDMOS工艺的AB类功率放大器。测试的正交相移键控(quadrature phase shift keying, QPSK)信号带宽为1 MHz。

首先通过矢量信号发生器产生QPSK信号，并由其完成基带到射频信号的转换。衰减器用于防止PA输出功率过大而烧坏频谱分析仪。其次，通过频谱分析仪获得PA的五阶非线性失真信号，频谱仪、矢量信号发生器与PC机均通过LAN口连接，PC机型号为20312且RAM为8 GB，由PC端通过LAN口完成对PA输入输出信号的采集，利用Matlab进行时延估计与校准，当时延校准满足精度要求时，对QPSK信号进行预失真处理。最后，通过LAN口将预失真信号加载至矢量信号发生器并发送到硬件链路，由FSW观测QPSK信号预失真前后时域与频域的变化，并重点观测邻道功率比(adjacent channel power ratio, ACPR)来验证DPD的线性化效果。

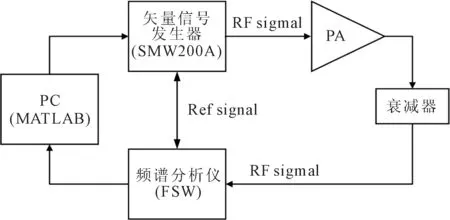
图2 实验测试环境

3.2 分数倍时延估计结果及分析

前向数据与反向数据通过实测得到，并使用Matlab仿真频谱结果。

(1) 算法仿真与分析

在固定分数倍时延为0.250 0TSI条件下，算法的估计结果如图3所示。可以看出，当估计时延为0.245 7TSI，估计误差为0.004 3TSI，可避免时延对DPD系统的影响[23]。在0.600 0TSI、0.052 0TSI时延下估计结果分别为0.591 7TSI与0.050 9TSI。

图3 时的时延估计结果

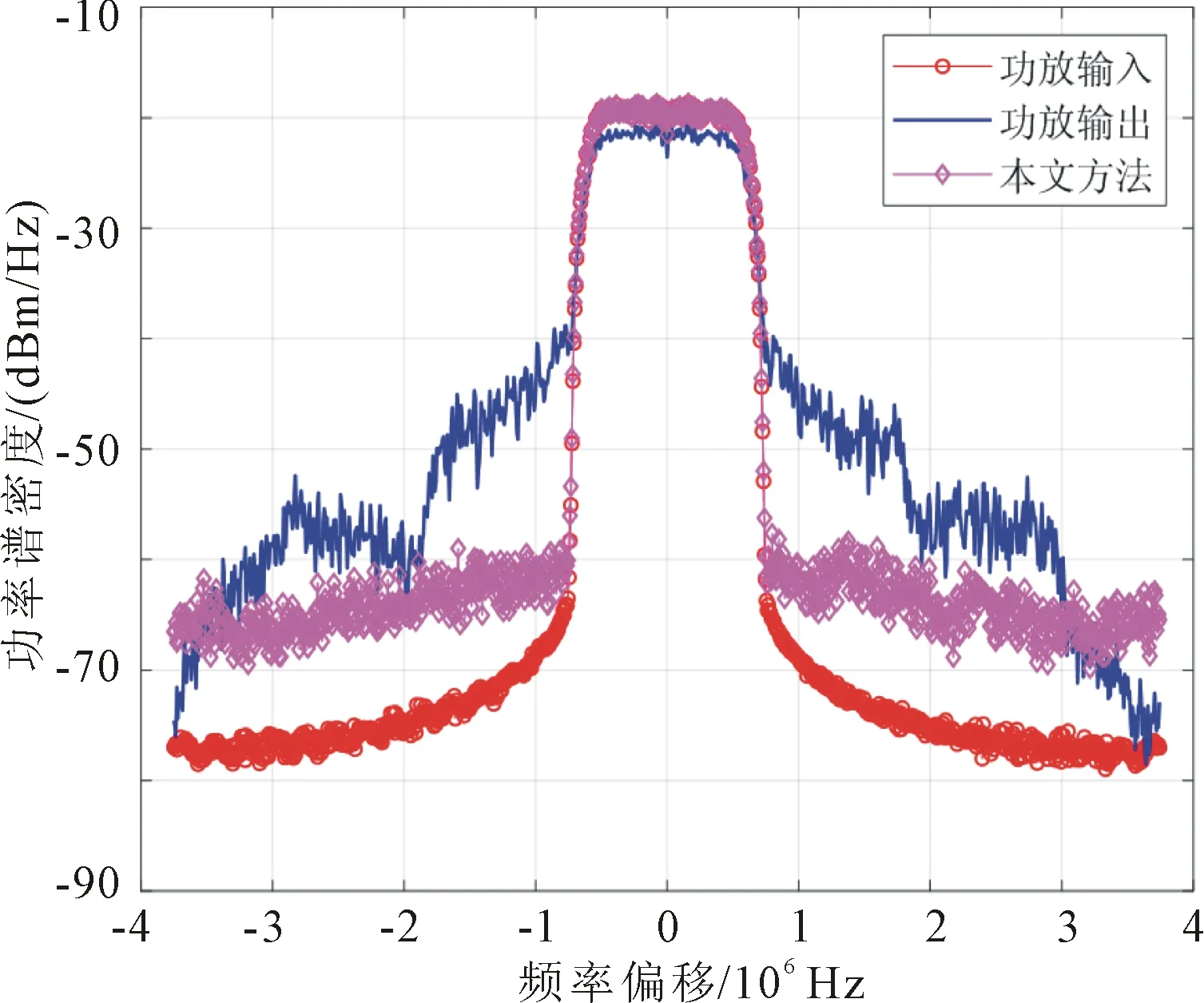
在PA输出功率为1dB压缩点即46 dBm条件下，不同分数倍环路时延经DPD处理与校正后，经DPD处理的幅调幅转换(amplitude modulation to amplitude modulation, AMAM)特性曲线和功率谱密度的对比，如图4所示。

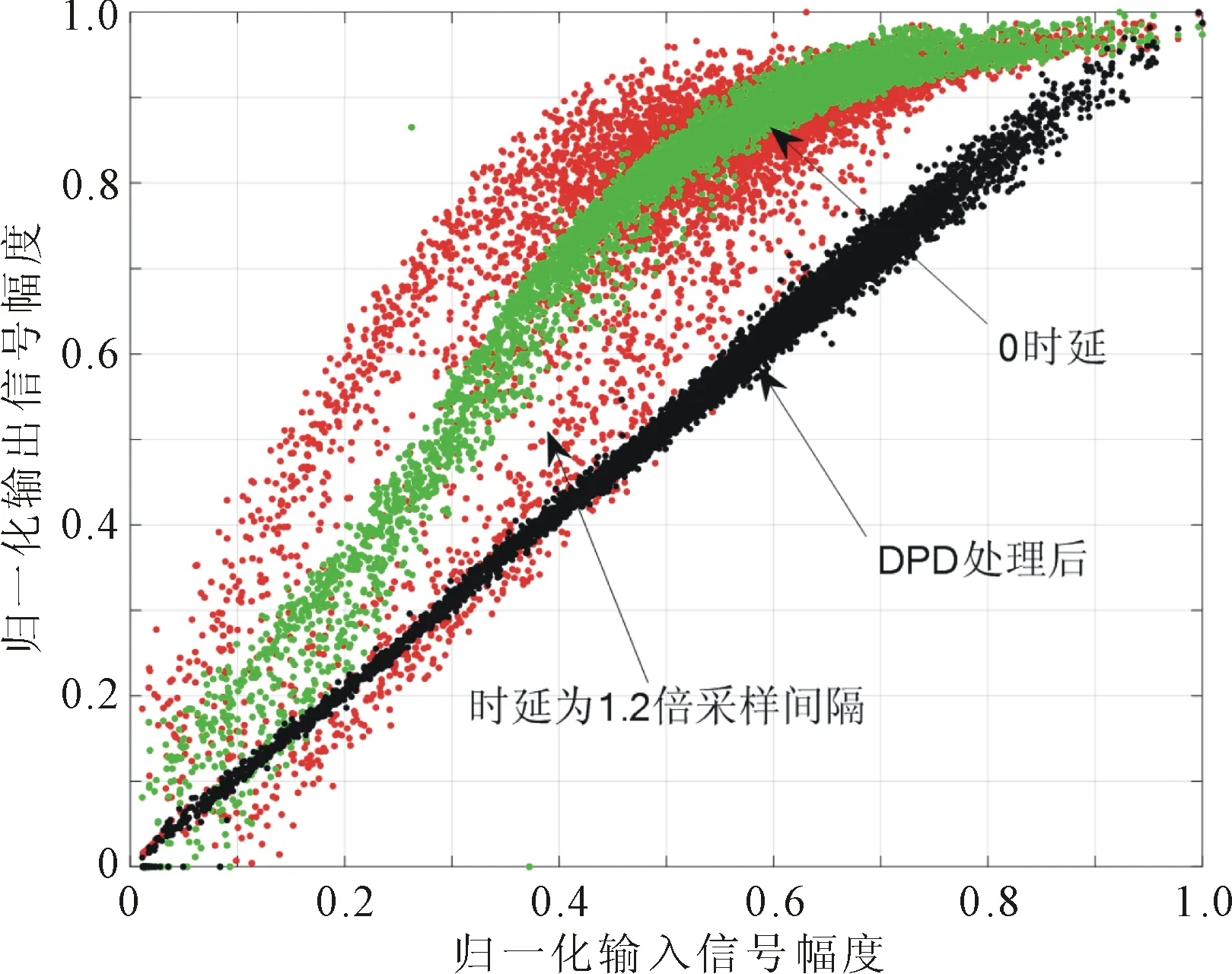
(a) AMAM特性曲线

(b) 时延与校正后预失真功率谱

(c) 时延校正算法的功率谱

从图4(a)可以看出，时延会造成AMAM曲线发散形成带内失真；图4(b)表明，分数倍时延越大对DPD的非线性校正能力影响越严重，对邻道的干扰越强，带外频谱扩散越严重；图4(c)为经过本文算法时延校正后的DPD对PA线性化的频谱结果，可以看出ACPR有明显改善。

在PA输出功率在1dB压缩点条件下，固定时延DPD仿真ACPR对比结果，如表1所示。

表1 固定时延DPD仿真ACPR对比

可以看出，即使环路时延仅为分数倍时，其对ACPR也会产生影响。当时延为0.600TSI时，ACPR值提升了约14 dBc；当时延为0.052TSI时，ACPR值提升了接近18 dBc，因此，环路时延越小对DPD线性化性能影响也越小。

(2) 复杂度与运算时间

根据式(1)可知，时域互相关方法估计整数倍时延的计算复杂度为O(N2)，并且在估计过程中需要N×τ次复数相乘，在相关性估计过程中，τ一般左右各移动N-1次，因此τ最大取2N-1。而式(2)方法需要两次FFT和一次IFFT计算，计算复杂度均为O(NlogN)，并且在此期间仅需要3/2Nlog2N+N次复数相乘与3Nlog2N次复数相加[10]。在分数倍时延的估计过程，使用内插时域互相关函数的运算量将随着插值倍数的增加而增加，而本文采用基于最小二乘法处理归一化频率方法，复杂度为O(N2)。

将本文算法与文献[6]的互相关内插的时延估计算法进行对比，不同时延校正算法的运行时间如表2所示。

表2 时延校正算法DPD运行时间仿真对比

可以看出，一方面，当积分偏移分别为-1 MHz和1 MHz时，文献[6]算法的ACPR分别为-40.83 dBc和-40.36 dBc，相较于表1中未加DPD的PA输出ACPR指标分别有17.90 dBc与16.50 dBc优化；本文算法的ACPR分别为-40.88 dBc与-40.40 dBc，分别有18.00 dBc和16.60 dBc的优化；本文算法优于文献[6]算法。另一方面，本文算法和文献[6]算法的平均运行时间分别为0.021 s、0.214 s，相较于文献[6]算法，本文算法运行平均时长降低了约90.1%。这是由于本文算法采用了快速傅里叶变换，提高了整数倍时延估计的速度；使用的频域相位差算法加快了分数倍时延估计，避免了插值和滤波操作，降低了算法复杂度、运算量和算法运行时间。

4 结语

提出了一种DPD系统环路时延的估计方法。该算法的整数倍时延由基带输入与反馈回路信号间圆周相关的傅里叶变换估计，分数倍时延根据频域相位作差的方式直接求解，最后通过广义记忆多项式DPD算法得到预失真信号。仿真结果表明，本文时延估计算法对ACPR指标的优化和文献[6]算法基本相同，同时降低了算法的复杂度和运行时间。