不同润湿性表面液滴铺展及蒸发过程的LBM数值模拟*
2019-09-05方可宁单彦广袁俊杰
方可宁,单彦广,袁俊杰
(上海理工大学 能源与动力工程学院,上海 200093)
0 引 言
固着液滴蒸发是指附着在固体壁面上的液滴蒸发过程。随着蒸发进行,液滴体积不断减小,同时液滴外部形状不断发生变化,不饱和蒸汽发生扩散。液滴蒸发过程涉及复杂的传热传质,受周围环境、基板温度、壁面润湿性以及液滴特性等因素影响。许多学者通过实验、理论以及数值模拟等方法做了大量研究工作。PICKNETT等[1]对固着在基板上的甲基乙酰乙酸液滴缓慢蒸发过程的质量及体积变化进行了研究,得出固着液滴蒸发过程中的两种模式:接触角不变模式和接触半径不变模式。BIRDI等[2]对玻璃基板上不同尺寸的纯水液滴和辛烷液滴的蒸发过程中液滴质量和接触角的变化情况进行研究,结果表明液滴蒸发速率由固着液滴的初始接触半径决定。此外,许多学者对亲水[3-5]或疏水[6-8]基板上的液滴蒸发过程中接触角、接触半径以及形状变化也进行了研究。由于实验研究难以通过对蒸发通量及蒸发速率的精确控制来总结液滴的传热规律,因此研究人员采用数值模拟的方法对蒸发相变过程进行研究。王宝和等[9]研究发现,随液滴蒸发过程的进行,因基板与液滴间的热量传递、蒸汽向大气环境中输送、液滴质量减少等因素,引起气液界面的变化,使得液滴蒸发过程内部流动复杂[10-11]。DUH等[12]提出液滴缓慢蒸发的数值模型,用于研究固着在等温基板上的液滴在蒸发过程中内部流场的分布情况。文章指出液滴内部的运动是由于流场内存在浮力和毛细对流,从而导致流场呈现多种结构。在此基础上,MARZO等[13]提出将一个半无限大固体与液滴耦合,利用有限体积法进行数值模拟,其中假定液滴在蒸发过程中保持球冠型,且液滴的体积变化与蒸发时间呈指数关系。在此基础上,饶玲等[14]将椭球冠模型用于模拟液滴蒸发过程,比对实际实验结果[1],相对于前人使用的球冠模型,椭球冠模型能更准确地描述实际的物理过程。
相对于目前普遍应用的计算流体力学方法(computational fluid dynamics, CFD),格子玻尔兹曼方法(Lattice Boltzmann Method, LBM)作为介观方法,由于其边界处理简便,不需要额外追踪界面等优点,已应用于不少相变传热传质问题研究。已经有学者建立了多种LBM模型,包括颜色流体模型[15-16]、伪势模型[17-18]、自由能模型[19]和动力学模型[20-21]。LEE等[22]提出不可压缩二元流体的边界条件改进,将模拟液滴撞击干燥表面的过程与实验结果进行对比,结果表明对于中等接触角的液滴能准确预测,但对大接触角的液滴则没有那么准确。此后,LATIFIYAN等[23]将二维流体模型与热格子结合,模拟了多孔介质中液体渗透过程,研究无量纲参数、孔隙度、接触角和密度比对穿透率及蒸发速率的影响。GONG等[24]对热格子模型进行改进,改进的模型可有效模拟多相流动和相变情况,而且能解决更大温度范围内的复杂流体问题。LI等[25]基于现有的蒸发相变模型和有焓变的固液相变模型,建立新模型模拟干燥饱和蒸汽瞬时冷凝后在倾斜的疏水基板上的冻结过程,指出重力和基板润湿性对液滴形态有重要的影响。
针对目前基于CFD方法模拟液滴蒸发大多忽略重力的影响,将液滴蒸发过程的外形近似为球冠形的局限,采用改进的热格子玻尔兹曼方法,研究重力场下基板润湿性和初始环境温度对纯液滴蒸发的影响,并考虑液滴在滴落基板后因与基板之间亲疏水性不同而导致的铺展或收缩过程,预测液滴蒸发过程内部流场、外形演变、接触直径以及剩余质量的变化。
1 数值模拟
1.1 多相流LBM模型
LBM通过流体粒子分布函数描述流场内固定格子的运动过程,演化方程为:

其中:x是计算流场内的一个格点;t为当前时间步;ei是流体粒子的离散速度;δt是离散的时间步长;τf为无量纲松弛时间;fi为流体粒子的速度分布函数。此外,为平衡态分布函数,其表达式为:

式中:u为格子速度;ωi为加权系数;cs为格子声速,在二维D2Q9模型中取值离散速度ei具体公式如下:


式中:Δu是在δt时刻由于力F导致的速度差,表示为其中,力项F表示为粒子点受到各项力的总和:

Fint(x)为各粒子间的相互作用力,表示为:

ψ(x)为粒子间的相互作用势,主要由粒子的密度ρ及压力p决定:

其中,c0为作用势系数,取值c0=6。
此外,β作为权重因子,用于提高数值计算的稳定性,根据状态方程取值不同,取值β=1.16。在二维D2Q9模型中,
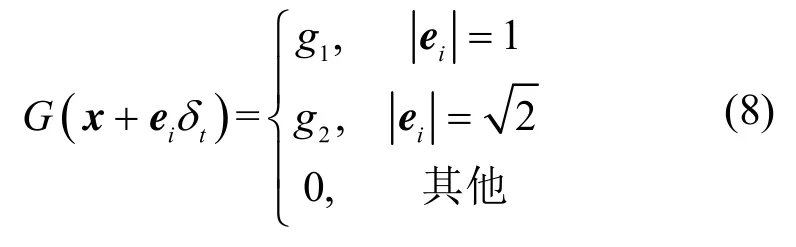
Fs(x)为流体与固壁面之间的相互作用力,表达式如下:

其中:gs表示流固相互作用强度的参数,用于控制基板的润湿条件;s(x)用于区别固-流两相,流体相s(x)=0,固体相s(x)=1。
Fg(x)为重力,可表示为:
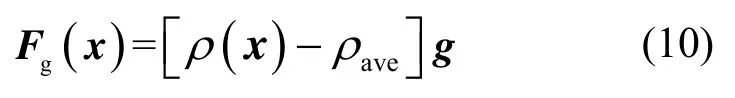
其中:g为重力加速度。
实际粒子的宏观密度及速度由下式得到:

但式(12)得到的速度并不是真正的实际速度,实际速度U需要考虑力F(x)的作用,表达式为:

由于模拟两相间的密度比较大,因此选用R-K状态方程能较好地模拟物理过程,其方程如下:

1.2 能量方程模型
温度分布函数描述流场内温度场的变化过程,演化方程为:

其中:τT为无量纲松弛时间;gi为流体温度分布函数;为参与气液相变的源项。
温度的平衡态分布函数[25]:

其中,相变源项由文献[24]得出,

温度可由统计计算得到:

1.3 模型验证
表1和表2给出了数值模拟中的格子单位和实际对应的参数值。如无特别说明,下文变量单位为表1的格子单位。

表1 格子玻尔兹曼方法中单位[26]Table 1 Units in Lattice Boltzmann Method

表2 模拟计算中参数值Table 2 Parameter value in simulation
1.3.1 Laplace 验证
模拟计算域在Lx×Ly内半径为R的悬浮液滴在环境温度恒定为Ts=0.9×Tc条件下最终稳定的问题。根据Maxwell重构方程可得,在Ts=0.9×Tc的环境温度下,液相初始密度为ρl=5.9079,气相密度为ρg=0.5801。为保证模拟结果有效性,分别取液滴初始半径为24、28、32、36和40的情况,进行模拟。计算域四周的边界条件均为周期边界条件。悬浮液滴在表面张力σ作用下保持球冠形,达到稳定后,求得液滴界面内外的压力跃变差值Δp=pl-pv的数值与半径的倒数1/R的关系。结果如图1所示,Δp=pl-pv与1/R呈线性关系,符合Laplace定律。

图1 Laplace验证Fig.1 Laplace validation
1.3.2 网格无关性验证
模拟计算域为Lx×Ly内固着液滴在加热基板上受重力作用的蒸发过程。同样根据Maxwell重构方程分别求出不同饱和温度下的气液两相临界密度,即对应初始密度的取值,基板润湿性为亲水,接触角θ=60°,即三相接触线所在的气-液界面的切线与基板间的夹角为60°,通过流固相互作用强度参数与接触角的拟合,即取重力加速度取值选用不同大小的网格数,对液滴蒸发过程中基板上液滴的高H与接触直径D之间比值的变化进行记录。每10 000次迭代计算输出一次结果,数据汇总见表3。
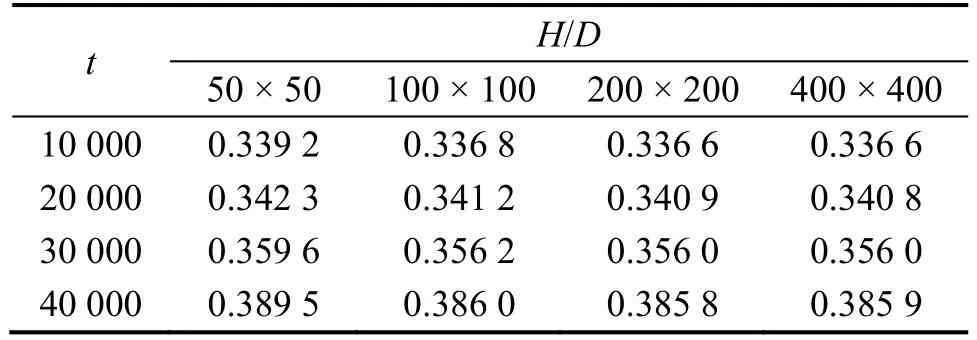
表3 网格无关性验证Table 3 Grid independence validation
由表3可知,不同网格数下的H/D值变化趋势基本一致,随蒸发进行而不断增大。网格数在50 × 50与100 × 100之间的H/D的最大相对差值为0.96%,网格数在100 × 100与200 × 200之间的相对差值最大为0.06%,而网格数200 × 200与400 × 400之间的最大相对误差为0.02%。因此计算域Lx×Ly选用200 × 200网格数进行模拟计算。
2 结果及分析
模拟计算域为Lx×Ly,假定液滴初始滴落到基板上呈半圆形(即接触角为90°)。受基板润湿性影响,液滴与基板接触后发生铺展或收缩现象,稳定后达到设定的静态接触角,然后开始蒸发直至蒸发完成。为简化计算,假定流体物性参数在蒸发过程中保持不变,忽略静压力对液滴蒸发的影响,加热基板为光滑基板,具体物理模型如图2所示。Lx×Ly恒定为200 × 200网格数,蓝色区域为初始半圆形液滴,放置在加热基板的中心位置,初始半径R=40,加热基板温度为Tw=0.9×Tc,初始环境温度Ts=0.85Tc,液滴初始温度与环境温度相等。据初始环境温度及Maxwell重构方程,气相及液相密度分别取ρg=0.5801、ρl=5.9079。该模拟计算域左右边界设置为周期性边界条件,系统为开放系统,因此上边界为对流边界条件,下边界出口为加热基板,设定下边界温度为加热温度,设置为无滑移边界条件。

图2 计算模型Fig.2 Calculation model
为了研究蒸发过程液滴形状的变化以及流体的传热流动特性,通过改变液滴重力及基板润湿性、初始环境温度等条件,模拟不同条件下的液滴蒸发过程,考察液滴接触直径、蒸发速率以及蒸发寿命的变化情况。其中液滴接触直径,即液滴与基板间的三相接触线直径,记为D。蒸发速率即计算域内液相质量变化量与初始液相总质量之比记为Vt,其中液相的定义为密度值的区域。蒸发寿命为液滴在加热基板上完全蒸干所需要的时间。对演化时间进行无量纲化,特征时间定义为同样,文中模拟变量均为LBM对应的无量纲单位。
2.1 重力对液滴蒸发过程的影响
为考察重力对液滴在加热基板上铺展及蒸发过程的影响,模拟考虑重力和忽略重力两种情况的铺展蒸发过程。基板润湿性为亲水,接触角θ=60°,流固相互作用强度参数和重力加速度取值同1.3.2节。
图3为液滴蒸发过程演化图。由图可知,两种情况下,受基板润湿性影响,液滴放置在基板直至稳定阶段,三相接触线均会发生铺展现象,但重力情况下的铺展现象更明显。稳定后液滴进行蒸发,液滴体积随蒸发时间不断减小,同时接触角基本不变,直至蒸发完成。相同时间内,重力情况下液滴蒸发更快,这是由于液滴受重力作用,液滴与加热基板的接触面积增大,通过接触面传递至液滴内部的热量也就更多,因此液滴在重力条件下能较快蒸干。

图3 液滴蒸发过程演化图Fig.3 Evolution diagram of droplet evaporation process
为验证上述结论,图4给出了液滴铺展及蒸发过程中接触直径随时间的变化趋势。由图4可知,液滴放置在基板后,受基板润湿性影响,接触直径逐渐增大至稳定。随后蒸发进行,液滴三相接触线不断收缩,接触直径随之减小,接触直径与时间呈幂指数减小关系,该现象与文献[27]结果一致。重力条件下,液滴铺展现象更明显,对应稳定后的接触直径较大。与文献[27]结果不同的是,重力情况下液滴接触直径减小速度较快,蒸发后期同一时刻液滴的接触直径相对较小,完成蒸发所用的时间也较短。

图4 液滴接触直径随时间变化趋势图Fig.4 Trend chart of contact diameter change in droplet evaporation process
图5给出了蒸发过程中液滴剩余质量随时间的变化趋势。由图可知,两种重力条件下,液滴剩余质量变化趋势基本一致,均随蒸发时间呈线性减小趋势。相对于无重力条件下的剩余质量变化,有重力情况下的斜率更大,即蒸发量较大,因而蒸发所需时间较短,能够较早完成蒸发。

图5 重力对液滴剩余质量随时间变化的影响Fig.5 Influence of gravity on the residual mass of droplets with time
由上述结论可知,重力场对液滴蒸发有不可忽略的影响,也即相较于常用的球冠模型,椭球冠液滴模型与实际过程更为接近[15]。因此研究均考虑重力场对液滴的初始铺展或收缩过程及蒸发的影响。
2.2 润湿性对液滴蒸发过程的影响
基板润湿性是影响液滴铺展及蒸发的重要因素,本节模拟不同基板润湿性条件下液滴铺展蒸发过程。考虑静态接触角为60°、90° 和120°,即gs取值分别为0.22、0.70、1.14。其余参数与上节相同。
图6为不同润湿条件下液滴铺展及蒸发过程的演化。可知基板润湿性表现为亲水时,液滴放置在基板后会发生铺展现象,直到接触角接近60° 时达到稳定。液滴蒸发过程,铺展稳定后的接触角保持不变,接触直径不断减小,直至液滴完全蒸干。当接触角为90° 时,液滴维持初始形状,不发生铺展。蒸发过程中液滴接触角不变,接触直径不断减小,直至液滴完全蒸干。当基板润湿性表现为疏水时,液滴在滴至基板后会出现收缩现象,直至液滴形状维持在接触角120° 时达到稳定。随后液滴继续蒸发,直至完全蒸干。比较三种基板接触角条件下的蒸发过程可以发现,相同时刻下,随着基板疏水性增强,残余液滴质量相对较大,即相应液滴蒸发较慢。

图6 不同润湿性条件下液滴蒸发过程演化图Fig.6 Evolution diagram of droplet evaporation process under different wettability conditions
为验证以上结论,考察基板接触角为60°、75°、90°、105° 和120° 五种情况下液滴的蒸发寿命,如图7。可知加热基板接触角越小,即越亲水,液滴蒸发寿命越短;基板接触角越大,液滴蒸发寿命相对较长。基板为疏水时,液滴的蒸发寿命随润湿性变化幅度更大。
为进一步分析基板润湿性对液滴寿命的影响,图8给出了不同基板润湿性条件下液滴接触直径随时间的变化情况。可知,亲水基板的液滴铺展稳定后的接触直径较大,随蒸发进行减小相对较快。接触角为90° 时液滴维持原状,不出现铺展或收缩现象,接触直径随时间变化基本呈幂指数相关,蒸发寿命相较亲水基板的液滴变化不大。疏水基板上的液滴在收缩稳定后,因接触直径较小,其减小趋势较缓,蒸发寿命较长。

图7 不同润湿性条件下液滴蒸发寿命变化图Fig.7 Diagram of droplet evaporation life under different wettability conditions

图8 不同润湿性条件下液滴接触直径随时间变化趋势图Fig.8 Trend chart of contact diameter change with time under different wettability conditions
图9为液滴剩余质量随时间的变化情况。可知在不同润湿性的基板上液滴剩余质量变化趋势基本一致,液滴初始质量相等,剩余质量均随蒸发时间呈线性减小趋势。

图9 不同润湿性条件下液滴剩余质量随时间变化图Fig.9 Diagram of droplet evaporation rate with time under different wettability conditions
结合图7和图8可知,基板接触角越小,液滴剩余质量变化越大,也就越容易蒸干。
2.3 初始环境温度对液滴蒸发过程的影响
为探究初始温度场(环境温度记Ts、基板温度记Tw)对液滴铺展及蒸发过程的影响,本节模拟研究不同环境温度下液滴铺展及蒸发过程。三个工况下的初始温度设置如表4所示,gs始终取值0.70。

表4 不同工况下初始温度Table 4 Initial temperature under different working conditions
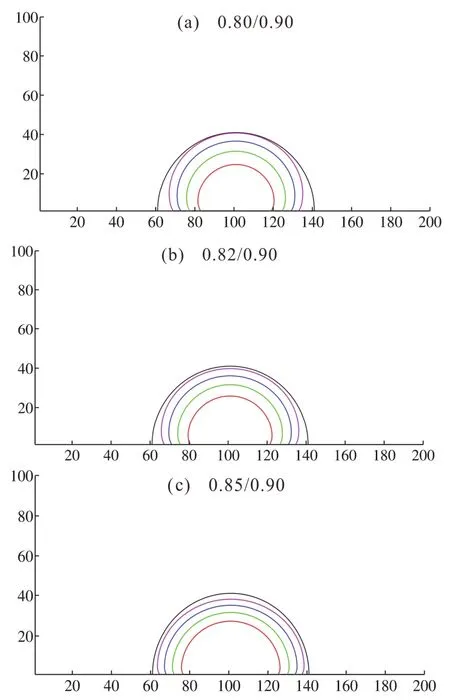
图10 不同环境温度下液滴蒸发过程演化图Fig.10 Evolution diagram of droplet evaporation process at different environmental temperatures
图10给出了不同环境温度下,液滴蒸发的演化过程图。由图可知,不同初始环境温度下液滴的铺展及蒸发过程趋势一致。液滴在加热基板上蒸发,整体形状逐渐变小,而接触角在蒸发过程中保持不变。初始环境温度与基板温度之间的温度差越大时,在同一演化时间,基板上残留的液滴质量更小,蒸发量较大,即蒸发速率较快。
为进一步考察初始环境温度对液滴铺展及蒸发过程中形状变化的影响,统计了不同工况下液滴接触直径随时间变化的趋势,如图11所示。由图可知,各工况下液滴接触直径变化趋势基本一致。液滴放置在基板直至稳定阶段,基本都存在不同程度的收缩过程,然后开始蒸发,其接触直径持续减小,直至完全蒸干。

图11 不同环境温度时接触直径随蒸发时间变化趋势图Fig.11 Trend chart of contact diameter change with time under different initial temperature fields
3 总 结
采用LBM模拟了固着在加热基板上纯液滴的铺展及蒸发过程,研究重力场、基板润湿性和初始环境温度对液滴蒸发过程形状变化、液滴铺展或收缩现象以及蒸发速率等传热规律的影响,结论如下:
(1)液滴蒸发过程中需考虑重力场的影响。重力作用下基板上液滴稳定后呈椭球冠,相较无重力液滴铺展面积更大,蒸发速率大,蒸发所需时间较短。
(2)基板润湿性不同,液滴铺展或收缩稳定后与基板的接触角不同。相同质量条件下,液滴与基板接触角越大,发生收缩现象稳定后接触直径越小,因此蒸发速率越小,所需的蒸发时间更长。
(3)环境与基板温度的温差较大时,传热驱动力更大,强化了热量传递,液滴蒸发更快。
