带裂缝圆弧曲梁面内振动方程的摄动解析
2019-09-05何文正徐林生
何文正,徐林生
(1.重庆交通大学 山区公路水运交通地质减灾重庆市高校市级重点实验室, 重庆 400074;2.重庆广播电视大学 城市建设工程学院, 重庆 401520)
曲梁在公路桥梁工程中已经得到广泛的应用,其动力特性是曲梁结构设计中所关注的重要内容,随着使用年限的增加,桥梁结构的强度和刚度将下降[1],在复杂的工作环境下可能会产生开裂损伤,如果曲梁出现裂缝,其动力特性就会产生变化,通过研究桥梁结构动力特性的变化来识别其损伤特性是当前一个重要研究课题。如何准确模拟和分析裂纹对桥梁工程的曲梁动力特性具有重要意义。
曲梁的振动问题国内外已有广泛的研究[2-7]。但由于曲梁计算理论十分繁冗和带损伤问题的复杂性,在现有曲梁的研究文献中,曲梁振动问题研究对象均为无损伤的完整曲梁,研究中均未考虑裂缝等损伤对曲梁的动力特性的影响;对于带裂缝结构动力特性的研究成果则主要集中在直线梁。现有的研究中裂缝模拟方法主要分两种:第一种为无质量转动等效弹簧模拟裂纹[8-10],该方法缺点在于模拟裂纹的等效弹簧模型计算复杂,且不能直接描述裂缝特性;另一种方法为直接将梁开口裂纹模拟成梁微段内的横截面折减,采用摄动法分析裂纹梁的动力特性。一些学者基于摄动理论对带开口裂缝桥梁的简支梁、悬臂梁以及连续梁[11-13]动力特性进行了研究 ,但是以上文献研究对象均为直梁,带裂缝曲线梁的动力特性及损伤识别理论还有待于进一步研究;目前本文基于圆弧曲梁面内自由振动微分方程,采用摄动法将裂缝损伤展开成一阶摄动,推导了带裂缝曲梁固有频率、模态振型的解析式,通过数值计算验证了所提公式的正确性,分析了不同损伤程度下的动力参数的的变化规律,为带损伤的曲梁动力特性及损伤识别理论研究作了必要准备工作。
1 带裂缝圆弧曲梁振动方程
1.1 带裂缝圆弧曲梁的基本计算模型
以等截面匀质圆弧曲梁(以下简称为曲梁)为研究对象,采用三维流动直角坐标系,沿曲梁形心轴的切向方向为x轴,圆心方向为z轴,垂直于曲线平面向下方向为y轴;坐标系符合右手螺旋法则,如图1所示。
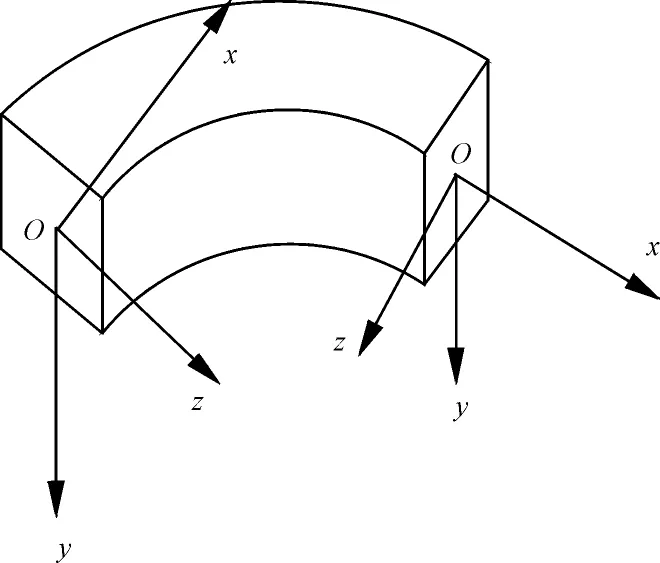
图1三维流动直角坐标系
图2为一矩形截面圆弧曲梁裂缝计算模型,曲梁梁半径为R,长度为l,横截面高度为h,宽度为b,假定在曲梁的xd处有一处裂缝,裂缝深度为hd,宽度为Δl,则损伤部分梁的截面惯性矩为:
(1)
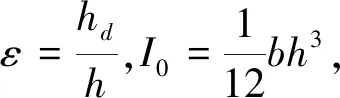
Id=I0(1-3ε)
(2)
同理,令m0=ρbh,ρ为材料密度,那么在梁的损伤部分,单位长度梁的质量为:
md=ρb(h-hd)=m0(1-ε)
(3)
如果在曲梁在xd处的小区域内存在裂缝,考虑在曲梁的全部长度上,其截面惯性矩的函数表达式可以用窗函数D来进行表示,定义窗函数
(4)
那么在梁的全部长度上,截面惯性矩的函数表达式为:
Id(x)=I0[1-3εD(x-xd)]
(5)
同理在梁的全长范围内,单位长度质量也可以用窗函数表示为:
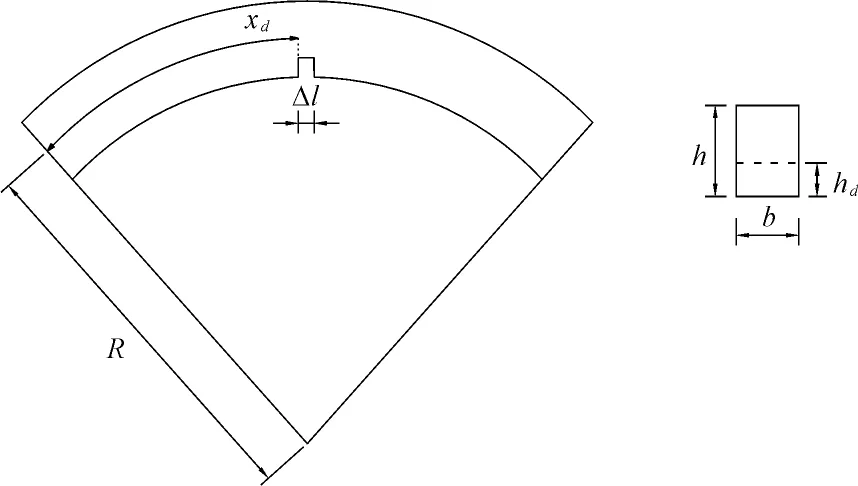
md(x)=m0[1-εD(x-xd)] (6)
图2带裂缝曲梁模型
由于弯扭耦合导致面外振动求解极为复杂,本文中暂只考虑面内振动的情况,文献[14]推导了单跨简支预应力圆弧曲梁面内振动微分方程,本文中直接引用该文献导出的方程,令预加力P=0即可得到无损伤状态下曲梁振动微分方程:
(7)
上式中v为曲梁的径向位移函数,采用分离变量法可以得到方程:
(8)
式中:λ为特征值;φ为振型函数。
在无损伤状态下弹性模量Id(x)和单位长度质量md(x)分别为常数I0和m0,可采用分离变量法[15]求解得到无损伤曲梁的第i阶特征值和振型函数:
(9)
(10)
其中Ai为任意非零常数。
将式(5)和式(6)代入式(8)可以得到带裂缝状态下曲梁的自由振动微分方程:
(11)
1.2 带裂缝曲梁动力学方程的摄动解
裂缝深度远小于截面高度,ε和Δl均为小量,假定开裂后曲梁的特征值和振型函数是开裂前的一个微小扰动,根据摄动理论,开裂后的特征值和振型可表示为:
(12)
(13)
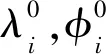
(14)
(15)
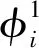
(16)
ηij为组合系数。
(17)
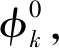
(18)
由积分中值定理可知:
(19)
(20)
(21)
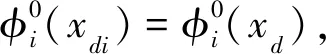
(22)
分别考虑当i=k和i≠k时的情况,可以求得:
(23)
(24)
将式(16)、式(23)、式(24)代入式(12)和式(13),进一步化简后得:
(25)
(26)
由式(25)和式(26)可以看出,当裂缝宽度或者裂缝相对深度为零的时候,振型和特征值的一阶摄动值均为零,即退化为无损伤状态下的曲梁特征值问题。
2 算例分析
2.1 数值验证和适用性分析
采用有限元数值分析方法验证所提方法的正确性和适用范围,无损伤状态的曲梁计算模型各物理参数见表1。

表1 曲梁物理参数
2.1.1 圆心角对自振频率的影响
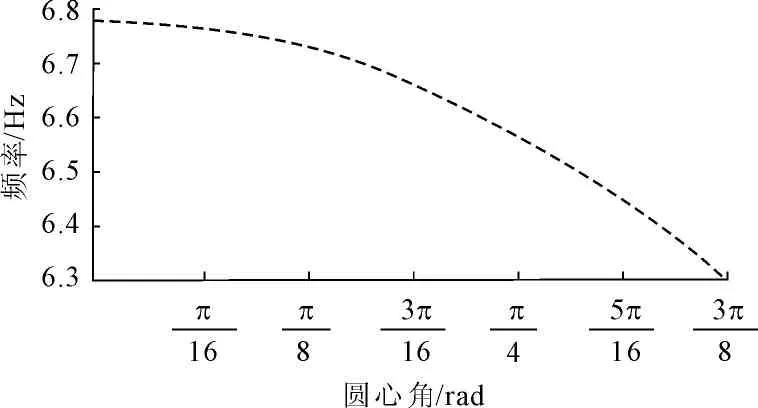
图3圆心角对曲梁自振频率的影响
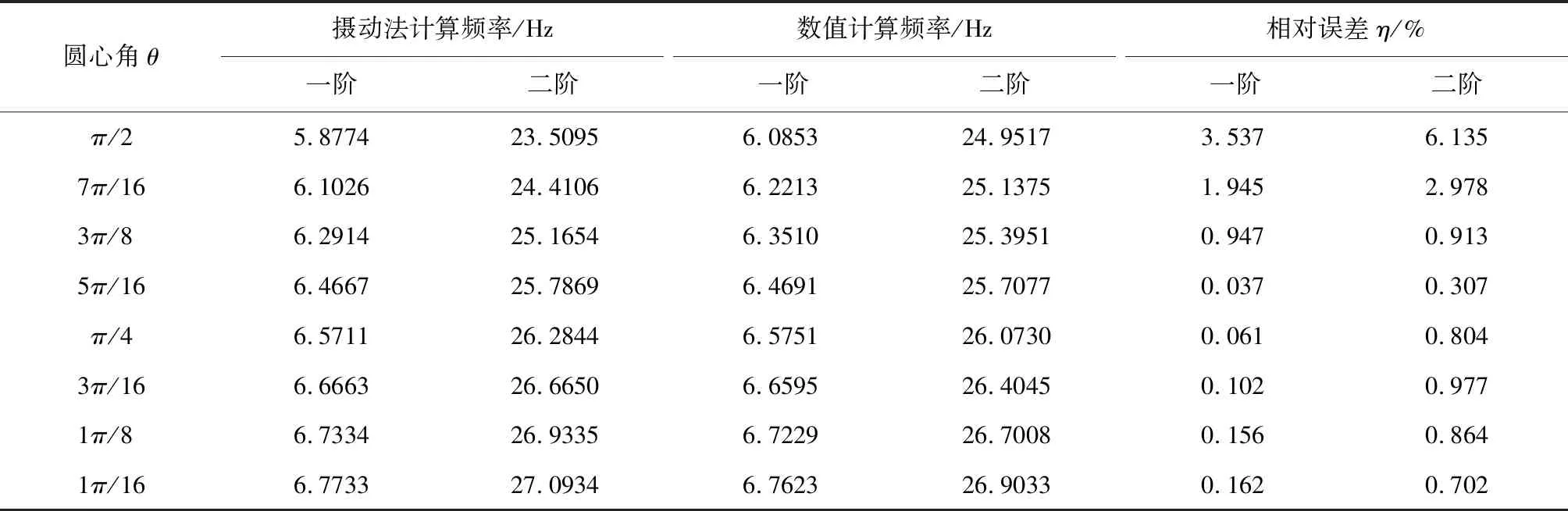
表2 不同圆心角曲梁自振频率计算结果
由表2可以看出,在梁长一定的情况下圆心角越小,自振频率越大,数值分析结果和理论分析结果一致,其中当圆心角θ=π/2时,理论结果与数值分析结果相比,一阶频率的误差为3.537%,二阶频率的误差为6.135%;随着圆心角的不断减小,相对误差也逐渐减小,当θ=3π/8时,一阶和二阶频率的误差均小于1%,本文提出的公式适用于圆心角θ=3π/8时的计算,当圆心角较大即半径过小的时候不宜用本文的公式进行计算,而应该考虑用拱的理论。
2.1.2 裂缝深度自振频率的影响
假定曲梁在跨中处存在裂缝,裂缝的相对深度ε分别取0.05、0.1、0.2、0.3、0.4、0.5,裂缝宽度取5 mm。采用梁单元模拟曲梁,裂缝采用截面高度折减方式模拟,进行特征值分析求解自振频率。运用式(25)计算带裂缝曲梁自振频率理论值,理论分析结果和数值分析结果见表3。
由计算结果表3可以看出,当裂缝相对深度小于等于0.3的时候,数值计算结果和理论计算结果吻合,其中一阶频率计算最大相对误差为0.265%,二阶频率最大相对误差为0.814%,误差较小。但是当裂缝相对深度大于0.3时,理论计算结果和数值分析结果偏差有增大趋势。这是由于摄动法本身适用于解决“小扰动”的问题,而当ε过大的时候已经不能再将截面的折减视为“小扰动”,此时本方法不再适用。
另外理论分析和数值分析都可以看出,裂缝位于跨中部位时,对一阶频率的影响较大,而对二阶频率几乎没有影响,这是因为裂缝所在的跨中位置位于一阶振型的峰值处和二阶振型的反弯点处。裂缝位置对动力特性的影响不可忽略。
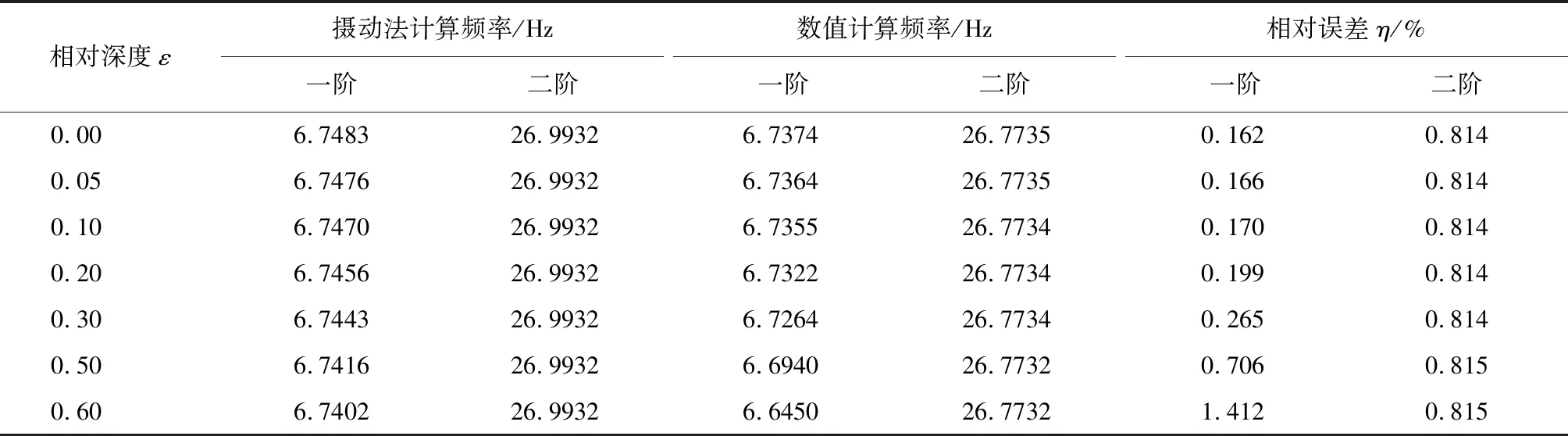
表3 跨中存在裂缝时频率计算结果
2.2 裂缝对动力特性的影响
由数值验证分析可知裂缝位置与曲梁动力特性的变化有很大的关系,裂缝深度和裂缝宽度都对自振频率有一定的影响;以前述曲梁为例,用式(25)进行计算,绘制裂缝深度和裂缝宽度对频率的影响图形,由于其他裂缝对一阶频率的影响与其他阶次频率的影响图形相差不大,文中只绘制了裂缝宽度和深度对一阶频率的影响图形,见图4;裂缝位置对一阶—四阶频率的影响见图5—图8。由计算结果可以看出,裂缝宽度和相对深度越大,频率降低越多,但总体上频率下降幅度很小,分析认为自振频率是一个整体的指标,而局部微裂缝对曲梁整体刚度和质量分布的影响很小,故局部的梁裂缝对曲梁自振频率影响较小,无法通过自振频率的变化来有效识别曲梁的损伤。
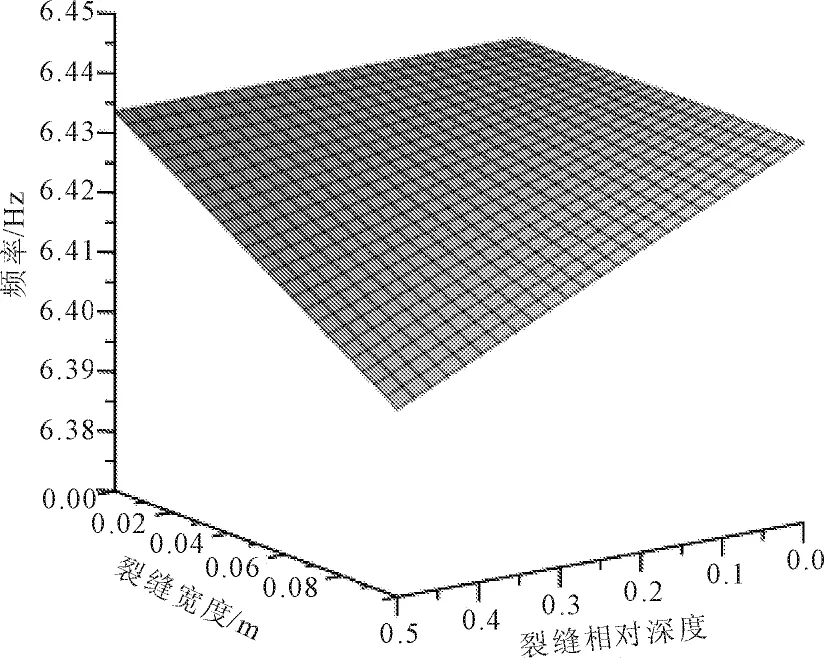
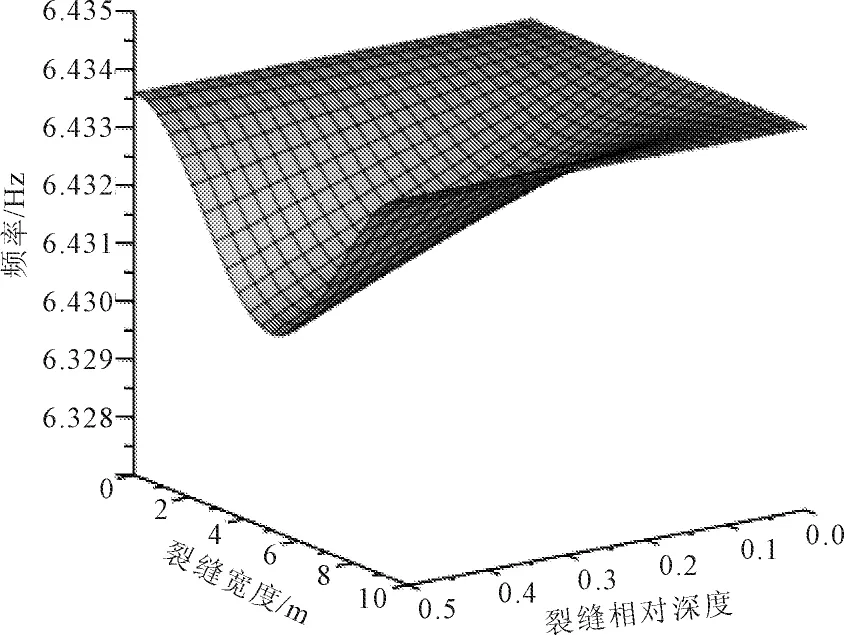
图4 裂缝宽度和深度对一阶频率的影响
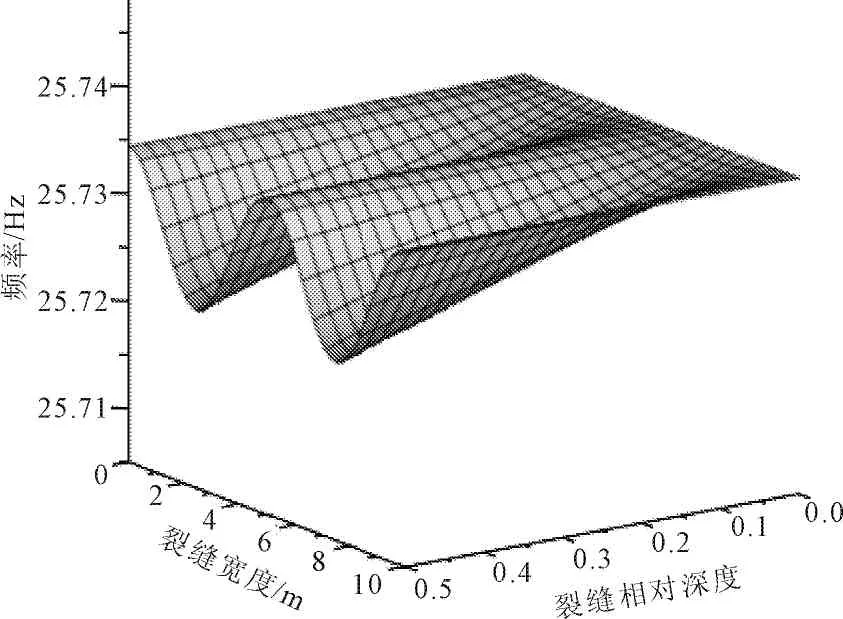
图5 不同位置裂缝对一阶频率的影响
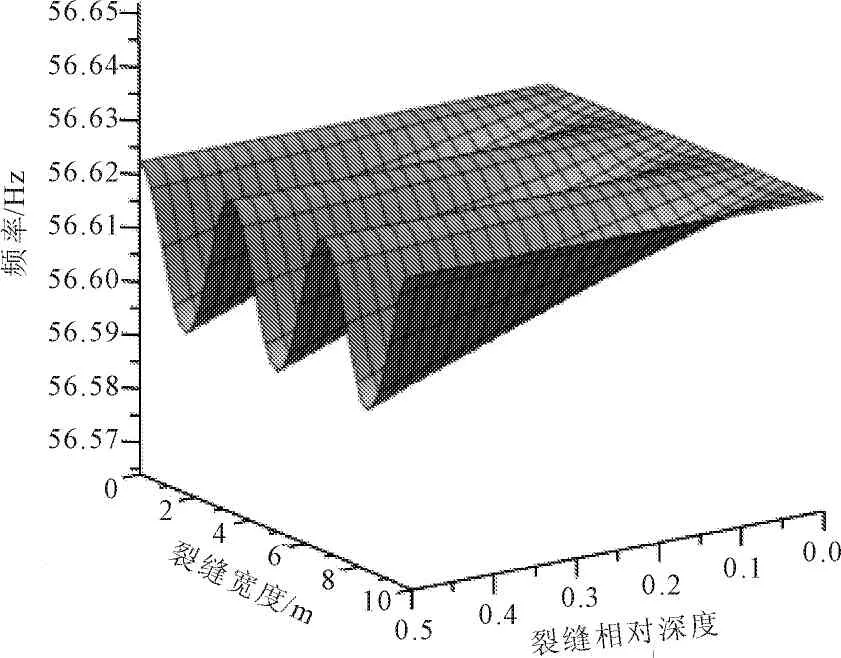
图6 不同位置裂缝对二阶频率的影响
图7不同位置裂缝对三阶频率的影响
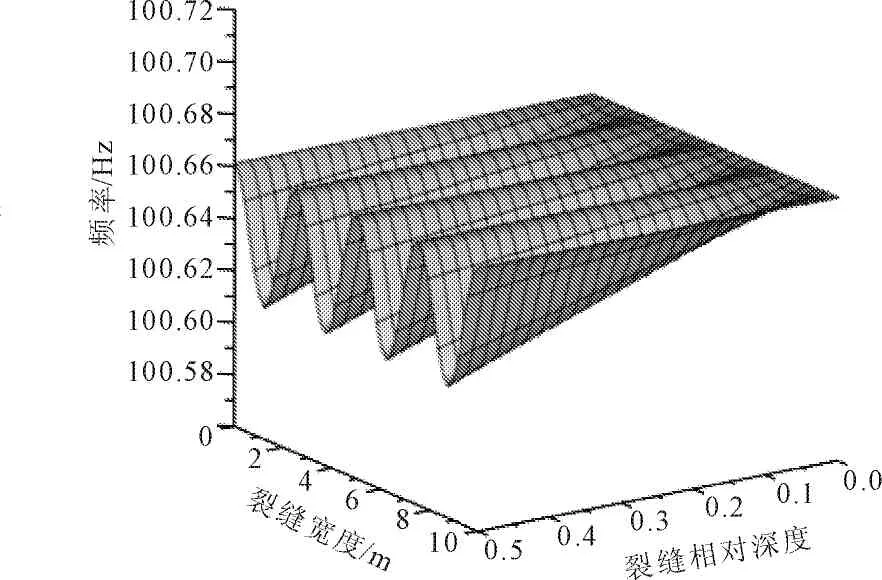
图8不同位置裂缝对四阶频率的影响
此外裂缝的位置对曲梁各阶次的频率变化有较大的影响,其影响与各阶次的振型有明显的相关性。当裂缝位于振型的峰值附近时影响较大,而位于振型的反弯点的时候则几乎没有影响。
3 结 论
推导了带裂缝曲梁振动微分方程,采用摄动法求解方程得到了带裂缝曲梁的面内模态频率和振型近似解析计算公式。进行数值计算验证了公式的正确性,分析了其适用范围,得到以下结论。
(1) 在梁长一定的情况下,本文的公式在圆心角θ<3π/8时有较高的计算精度,但是θ>3π/8时会有较大的误差,此时应考虑使用拱的理论。
(2) 随着裂缝深度和裂缝宽度越大,曲梁自振频率下降越多,且裂缝位置对曲梁各阶次的频率的影响与各阶次的振型形状相关;但是当裂缝损伤程度较小的情况下,带裂缝曲梁的动力特性与完好曲梁相差不大。
