RV减速器摆线轮动特性仿真分析
2019-09-05戚厚军
谭 鹏 戚厚军
(天津职业技术师范大学,天津市高速切削与精密加工重点实验室,天津 300222)
0 前言
RV减速器是在传统针摆行星传动的基础上发展出来的一种新型传动机构,不仅克服了一般针摆行星传动稳定性不高的缺点,而且具有体积小、重量轻、效率高、传动平稳等一系列优点,广泛应用于工业机器人、精密机床等装备中[1]。RV减速器在工作过程中由于齿轮之间的激振力而产生振动和噪音,影响减速器的传动性能,其中,摆线轮是影响RV减速器振动特性的关键零件[2]。
近几年,国内外学者在减速器振动方面做了大量的研究工作,取得显著成果,但涉及RV减速器振动的研究还不多。陈李果等人建立了RV减速器的试验装置和振动测试,通过测试掌握了减速器的振动特性[3];王文军等人考虑系统刚度和摆线轮的偏心角对扭转振动特性的影响,建立了13个自由度的动力学模型[4];严细海等人采用集中参数法建立RV减速器的5自由度纯扭转动力学模型,分析出其关键因素,通过试验得出模型的有效性[5];孙永森通过有限元模态方法研究了摆线轮的材料特性对其固有频率和振型的影响,进一步分析了影响摆线轮疲劳寿命的主要因素[6]。
本文主要对RV减速器中摆线轮进行有限元分析,根据与整机的固有频率对比结果,得出了摆线轮结构的优化方案,为RV减速器的结构优化设计提供了理论依据。
1 RV减速器的传动原理
RV减速器传动机构分为两级,如图1所示,第一级为中心轮与行星轮相啮合的减速机构,第二级为摆线轮与针齿相啮合的减速机构。各部件的具体联接关系如下:输入轴1是齿轮轴,一端与电机相联,另一端与行星轮2相啮合;行星轮2通过渐开线花键孔与曲柄轴3相联,曲柄轴3是第二级摆线针轮行星传动的输入轴;摆线轮和曲柄轴之间的轴承无内外圈,滚动体与曲柄轴和摆线轮孔壁直接接触;为了使整个机构达到静平衡,减少振动并提高传动的承载能力,采用互成180°放置的摆线轮。

1.中心轮 2.行星轮 3.曲柄轴 4.摆线轮 5.针轮 6.输出盘
2 摆线轮参数化建模
2.1 建立摆线轮的参数化方程
摆线齿轮的齿廓曲线为短幅外摆线,其原理是半径为r的滚圆在半径为R的基圆上做纯滚动时,该滚圆内一点的轨迹称为外摆线。韩林山等人通过对RV减速器摆线轮的三维参数化设计,其在直角坐标系下的方程可写为如下形式[7]:
x=c+rza,y=d-rzb,z=0
(1)
(2)
式中:Zc为摆线轮齿数;Zb为针齿数;Rz为针齿中心圆半径;K1为变幅系数;rz为针齿半径;t为0~1的系统变量;
2.2 摆线轮的精确参数化建模
以RV-80E减速器的摆线轮为例,其主要参数如表1所示。在SolidWorks中通过“草图”任务栏中的样条曲线下的方程式驱动曲线方式来创建摆线轮曲线,如图2所示,然后通过拉伸剪切等命令创建摆线轮实体模型,如图3所示。
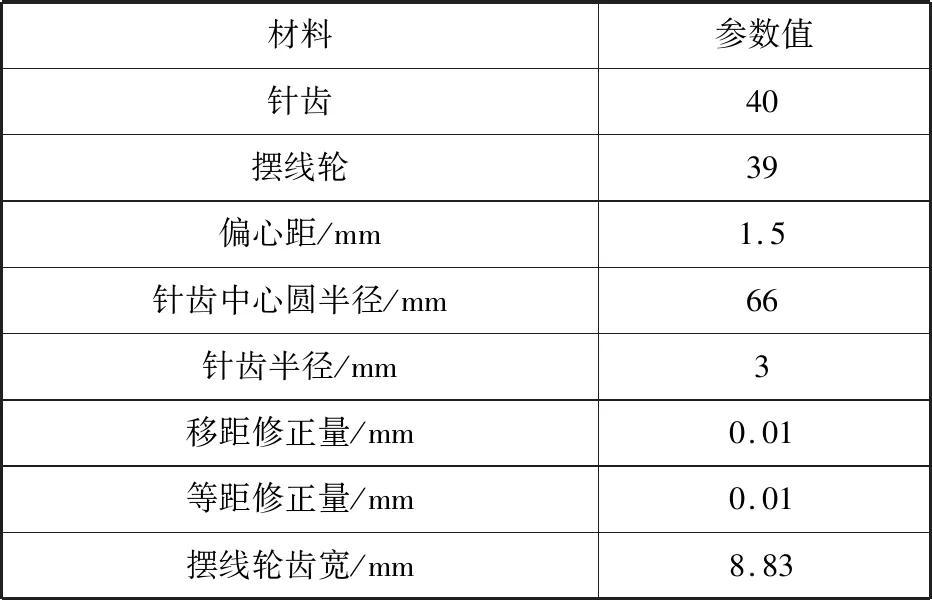
表1 RV减速器主要参数

图2 摆线轮的轮廓曲线

图3 摆线轮实体模型
3 摆线轮有限元模态分析
(1) 添加并导入材料
定义摆线轮的材料为Steel,密度为ρ=7.6 g/cm3,弹性模量E1=206 GPa,泊松比u=0.277,材料定义完成后,导入ANSYS环境中。
(2) 划分网格
为了尽可能的接近实体零件状态,得到较为均匀的网格密度,经最终网格划分,摆线轮共有86599个节点,42584个单元。如图4所示。

图4 摆线轮网格模型
3.1 摆线轮自由边界下的模态分析
经过ANSYS模态计算后,得到摆线轮自由边界下前10阶固有频率和振型,如表2所示,振型如图5、6所示。

表2 自由边界下的固有频率
根据以上结果可知,第1阶固有频率为0,分析过程中不考虑刚体模态,主要考虑2-10阶柔性模态的频率和振型。肖君君等人通过求解动力学方程得到了RV减速器系统前10阶固有频率分别为75.2、435.7、835.6、1678.4、2426.3、4115.3、4844.6、5847.5、7163.1、7921.5 HZ[8]。

图5 第四阶振型

图6 第七阶振型
通过比较得出,摆线轮的第四阶和第七阶与RV减速器穿透孔结构参数以便减速器传动系统的第四阶和第七阶固有频率相近,可能会产生共振现象,为此,改变摆线轮的材料参数或改变摆线轮的固有频率,进而避免传动系统共振的产生。观察振型图可以发现,摆线轮的最大位移处发生在摆线轮穿透孔处和摆线轮齿廓处,则说明此处变形较大。
3.2 摆线轮约束下的模态分析
在摆线轮的实际传动中,其自身是不可能不受约束的,而分析在实际约束下边界条件的模态,更能准确的反映出摆线轮在传动过程中的实际轮廓线形状。基于建立摆线轮参数化三维模型的基础上施加约束,即摆线轮在工作过程中主要受3个转臂轴承的约束跟与针齿之间的啮合约束,转臂轴承主要连接曲柄轴与摆线轮,所以需要在轴向方向上施加约束。仿真后得到固有频率如表3所示,振型如图7、8所示:
根据结果分析,可以发现约束边界下的固有频率大于自由边界下的固有频率,摆线轮的第七阶和第九阶与系统的第八阶和第十阶固有频率相近,可能会产生共振现象。
4 结构优化设计
(1) 根据上述模态分析结果显示,摆线轮存在着与系统较为接近的固有频率,在保证摆线轮刚度的基础上,尝试用改进摆线轮穿透孔结构的方法来优化,原有模型的穿透孔以扇形结构在摆线轮上均布,但降低了靠近齿廓处的孔边缘上的齿厚。现将摆线轮穿透孔改进为圆形均布在圆周上,并对优化后的结构进行验证。
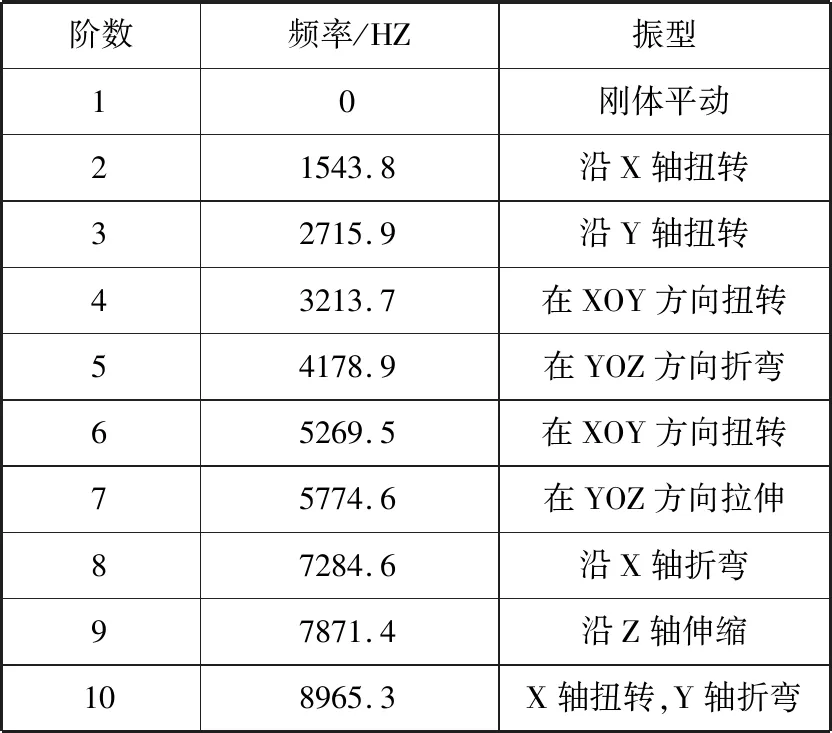
表3 约束下的固有频率
图7 第七阶振型

图8 第九阶振型
对改进的模型模态进行分析,得到固有频率和振型,为了便于比较,将各阶频率绘制成曲线的形式进行比较分析,如图9、10所示。在自由模态下的固有频率与之前相比较,2-5阶固有频率下降不太明显,但6-10阶固有频率下降较为明显,能较好的避免共振发生。同理,约束下的固有频率与之前相比较,各阶固有频率下降较为明显,可以避免共振的发生,此方案可行。

图9 约束边界下的固有频率对比
(2) 变更摆线轮材料的方式。选择弹性模量更大的材料GCr15,增加摆线轮的刚度属性进行优化。更改后的材料密度为ρ=7.9 g/cm3,弹性模量E1=219 GPa,泊松比u=0.3。得到的固有频率与原材料固有频率比较,得到如图11、12所示的曲线结果。在自由模态下,固有频率2-5阶下降不太明显,但6-10阶下降较为明显。约束条件下各阶固有频率下降较为明显,可以避免共振的发生,此方案可行。
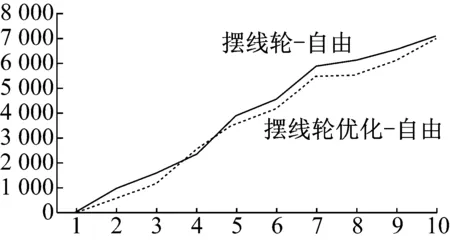
图10 自由模态下的固有频率对比

图11 自由模态下的固有频率对比

图12 约束边界下的固有频率对比
5 结论
(1) 通过在SolidWorks中建立了精确的参数化模型,通过修改参数可以快速生成新的模型,提高了建模效率,缩短了建模周期,有广泛的适用性。
(2) 通过ANSYS软件仿真分析,能够真实的表明摆线轮在实际的受力状态,明确较大应力分布区域,通过对比分析得到固有频率与整机的频率,找出了产生共振的频率,为降低共振提供了理论依据。
(3) 对摆线轮进行了结构优化,对比优化前后的分析结果,得出了优化后的模型对频率以及振型的影响效果,验证了改善的有效性。
