设计参数对幂次乘波体纵向静稳定性的影响
2019-09-05王晓朋张陈安王发民叶正寅
王晓朋,张陈安,刘 文,王发民,叶正寅
(1. 西北工业大学翼型叶栅空气动力学国防科技重点实验室,西安 710072;2.中国科学院力学研究所高温气体动力学国家重点实验室,北京 100190)
0 引 言
乘波体通过附着在前缘线上的激波将高压气体限制在其下表面,而获得高升阻比,且其下表面流场均匀、横向流动较弱,非常适合于乘波体-发动机的一体化设计。此外,在已知流场中构建乘波体的反设计生成方法有利于根据任务需求进行飞行器的灵活设计。由于其优良的气动性能和设计特点,乘波飞行器已经成为一种有潜在应用价值的高超声速气动布局形式。
文献[1]在1959年首次阐述了乘波体的构型思想,其以绕楔形体的流场为基准流场,在流场激波面上任意做一条曲线,从该曲线出发的所有流线构成的流面作为乘波体下表面,以自由来流平面作为上表面,生成了“Λ”型乘波体。因其能够突破“升阻比屏障”,得到了研究者的广泛关注。但“Λ”型乘波体容积率小,升阻比优势并不明显。随后,文献[2-3]基于圆锥绕流流场得到了升阻比更高,容积更大的锥形流乘波体。但这类乘波体是基于无黏流场得到的,在考虑黏性效应后升阻比下降明显。对此,文献[4-5]在乘波体的优化设计过程中首次将黏性效应考虑进去,通过单纯形加速法优化,得到了黏性优化乘波体。文献[6]采用CFD数值模拟详细研究了黏性优化乘波体在设计工况、非设计工况以及前缘钝化后的气动特性,论证了黏性优化乘波体的高升阻比特性,又进一步推动了乘波体构型理论的发展。随后,更多的乘波体构型和优化设计方法被提了出来[7-11]。对此,文献[12]做了详细总结。
总体而言,目前在乘波体的构型和优化设计过程中,升阻比和容积率是主要的关注对象,而对于飞行器的稳定性则在设计中关注较少。此外,传统飞行器中采用的安定面、舵面设计对于高空、长航时高超声速飞行器而言,面临着复杂的气动热问题,为飞行器的安全飞行带来了诸多的不确定性。
文献[13]以流线微元为研究对象,结合牛顿流理论、活塞理论和切楔切锥等工程算法,通过理论推导得出结论:乘波体的纵向静稳定性与构成乘波体下表面的流线“凹凸”特性有关,“内凹”型流线不利于乘波体的纵向静稳定,而“外凸”型流线有利于乘波体的纵向静稳定。由此,文献[13]进一步指出:基于锥型流场的锥导乘波体的下表面流线因处处具有“内凹”特征,难以满足纵向静稳定;而基于幂次锥型流场的幂次乘波体外形由于下表面流线具有“外凸”特性,不仅能够获得较大的容积率,也能获得满足纵向静稳定的气动布局。
在上述研究背景下,本文通过数值计算的方法,分析了构成幂次乘波体下表面流线的“凹凸”特性,研究了幂次乘波体设计参数与流线“凹凸”特性之间的相关性,并以文献[13]作为理论基础,进一步分析得到了设计参数与乘波体纵向静稳定性之间的关系,为幂次乘波体的纵向静稳定性设计提供了参考依据。
1 幂次乘波体的生成
幂次体是由定义在XZ平面上的幂函数曲线z=c(Lb-x)n绕X轴旋转一周生成,其中Lb为幂次体基准流场总长。通过调整参数c,n和Lb,可灵活调整乘波体外形。在来流条件确定的情况下,本文通过求解欧拉方程来生成幂次体的基准流场,采用三次样条曲线拟合的方式捕获基本流场的激波面,并在激波面上设置前缘点进行流线追踪,生成乘波体,生成过程如图1所示。在实际操作中,一般采用在基准面的左半平面或右半平面上定义前缘投影线(本文在右半平面定义前缘线),然后求出投影线在激波面上的对应坐标作为前缘点,随后进行流线追踪生成乘波体下表面,具体生成过程参见文献[14]。为验证本文生成幂次乘波体方法的准确性,取Lb=185 m,c=1,n=0.7,在Ma=15的设计工况下生成幂次乘波体,如图2所示。由图2可知,在无黏工况下,激波完全附着在前缘线上,下表面高压气体没有上溢,说明本文所采用的幂次乘波体生成方法是准确的。
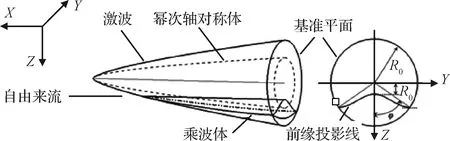
图1 幂次乘波体生成示意图Fig.1 Generation of power-law waverider

图2 幂次乘波体流场压力分布图(Ma=15)Fig.2 Pressure distribution around the power-law waverider (Ma=15)
2 设计参数与幂次乘波体下表面流线“凹凸”特性的关系
鉴于幂次体流场的轴对称性,本节将在二维平面内讨论激波面后流线的“凹凸”特性。同文献[13]一样,本文以流线的二阶导数y″即流线的曲率来定义流线在该点的“凹凸”特性,y″(x)>0表示流线在该点“外凸”,y″(x)<0表示流线在该点“内凹”。
2.1 幂次乘波体下表面流线的“凹凸”特性
设定幂函数曲线参数Lb=185 m,c=0.3,n=0.75,在设计工况Ma=10的流场中生成基准流场。在激波面上选取距幂次体头部横坐标距离dx0=85 m处的点作为前缘点进行流线追踪得到流线,如图3所示。沿X方向每隔0.25 m选取一个点计算流线在该点的二阶导数y″(x),结果如图4所示(横坐标表示距前缘点的距离,下文与此一致)。从结果来看,激波面后的流线逐渐向壁面靠近并分为两部分:靠近激波面y″(x)小于0的“内凹”段和靠近壁面y″(x)大于0的“外凸”段,且随着流动的进行,流线的曲率保持“外凸”。
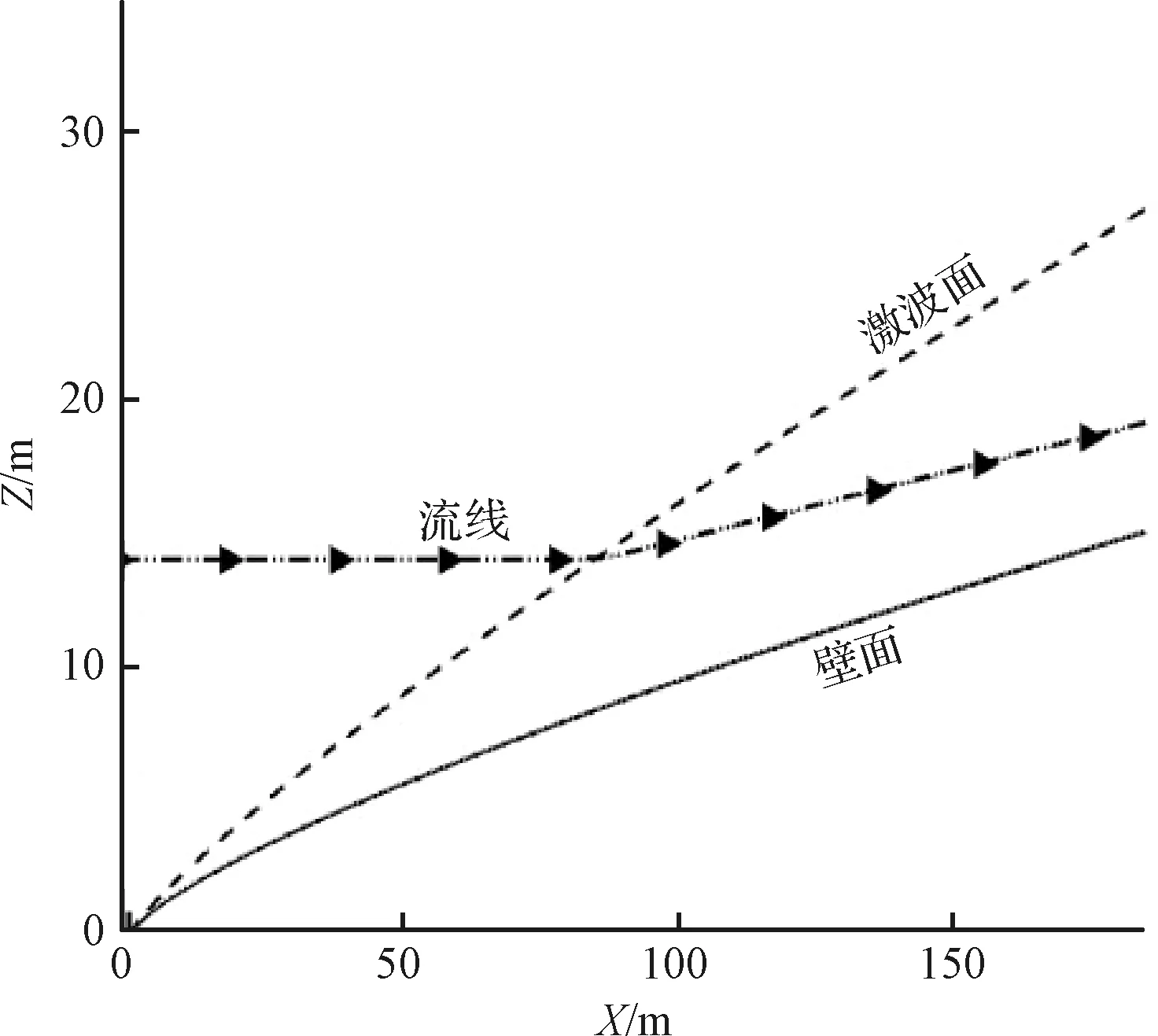
图3 幂次体基准流场Fig.3 Basic flow field around the power-law body
产生这种现象的原因在于:在激波面上流体由于受到激波压缩效应的影响,流线在激波面处表现为“内凹”;激波面后,由于幂次体曲率小于零,流体在流动的过程中会受到壁面膨胀效应的影响,流线的几何特征也逐渐由“内凹”转变为“外凸”,并随着流动的进行逐渐与壁面几何特征趋近。本文为了表述方便将流线几何特征由“内凹”转变为“外凸”的点称为特征分割点。
从以上计算和分析结果可以看出,由于受到激波压缩和壁面膨胀效应的影响,生成幂次乘波体下表面的流线并非处处都是“外凸”的,而是由“外凸”和“内凹”两部分组成。因此,研究设计参数与乘波体下表面流线凹凸特性之间的关系是必要的。
2.2 设计参数对流线“凹凸”特性的影响
2.2.1前缘点位置对流线“凹凸”特性的影响
设定幂函数曲线参数Lb=185 m,c=0.3,n=0.75,在设计工况Ma=10的流场中生成基准流场。在激波面上分别选取距幂次体头部横坐标距离为dx0=5 m,dx0=45 m和dx0=85 m处的点作为前缘点进行流线追踪,如图5所示。计算流线上各点的二阶导数,结果如图6所示。

图5 基准流场中的流线Fig.5 Streamlines in the basic flow field

图6 前缘点对流线“凹凸”特征的影响Fig.6 Influence of leading edge point on “concave-convex” characteristics of streamlines
由图6可知,尽管三条流线的“凹凸”特性沿流线发生转变的趋势是一致的,但流线的特征分割点的位置是不同的。dx0=5 m时,对应流线的特征分割点距前缘点的距离s=3.5 m;dx0=45 m时,s=10.5 m;而dx0=85 m时,s=15 m。不难发现,前缘点的位置与特征分割点之间存在如下关系:前缘点设置的越靠后,对应流线的几何特征分割点距该前缘点的距离s也就越大,即流线“内凹”段越长。其原因在于:前缘点位置越靠后,基准流场的激波面与壁面的距离越远,壁面的影响越小,因此需要更长的距离才能促使流线的几何特征发生转变。
2.2.2参数c对流线“凹凸”特性的影响
设定幂函数曲线参数Lbasic=185 m,n=0.75,c=0.2,0.3,0.7,在设计工况Ma=10的流场中生成三个不同的基准流场。在三个不同流场的激波面上选取距幂次体头部横坐标距离为dx0=5 m的点作为前缘点并进行流线追踪,如图7所示。计算流线上各点的二阶导数y″(x),结果如图8所示。

图7 基准流场中的流线Fig.7 Streamlines in the basic flow field

图8 参数c对流线“凹凸”特性的影响Fig.8 Influence of parameter c on “concave-convex” characteristics of streamlines
由图8可知,不同流场中三条流线的“凹凸”特性发生转变的趋势是一致的,但随着参数c的变化,流线特征分割点与前缘点之间的距离s发生了变化。c=0.2时,s=7 m;c=0.3时,s=3.5 m;而c=0.7时,s=1 m。显然,随着c的增大,对应流线的几何特征分割点距前缘点的距离越来越小,即流线“内凹”段的长度越来越小。其原因在于:随着参数c的增大,激波增强,激波与壁面之间的距离变小,幂次函数曲线曲率绝对值变大,壁面的膨胀效应增大,对流线的影响也更明显,因此只需要更小的距离就能促使流线的几何特征发生转变。
2.2.3参数n对流线“凹凸”特性的影响
设定幂函数曲线参数Lb=185 m,c=0.3,n=0.6,0.75,0.9,在设计工况Ma=10的流场中生成三个不同的基准流场。在三个不同的激波面上选取距幂次体头部横坐标距离为dx0=5 m处的点作为前缘点进行流线追踪,结果如图9所示。计算不同流线上各点处的二阶导数y″(x),结果如图10所示。
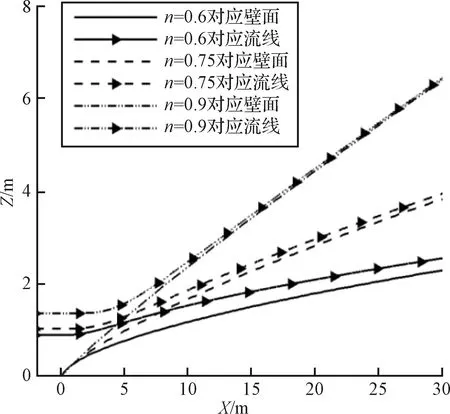
图9 基准流场中的流线Fig.9 Streamlines in the basic flow field

图10 参数n对流线“凹凸”特性的影响Fig.10 Influence of parameter n on “concave-convex” characteristics of streamlines
由图10可知,不同流场中三条流线的“凹凸”特性发生转变的趋势是一致的,但随着参数n的变化,流线特征分割点与前缘点之间的距离s发生了变化。n=0.6时,s=0.5 m;n=0.75时,s=3.5 m;而n=0.9时,s=7 m。显然,n越小,对应流线的几何特征分割点距前缘点的距离s越小,即流线“内凹”部分的长度越小。其原因在于:随着参数n的减小,幂次函数曲线曲率绝对值变大,激波增强,激波与壁面之间的距离变小,并且曲率的变化也导致了壁面的膨胀效应增强,因此,流线在更短的距离内就可以发生特征转变。
2.2.4设计马赫数对流线“凹凸”特性的影响
设定幂函数曲线参数Lb=185 m,n=0.75,c=0.3,在三个不同设计工况Ma=8, 10和15的流场中分别生成不同的基准流场。在三个不同的激波面上取距幂次体头部横坐标距离同为dx0=5 m的点作为前缘点进行流线追踪,如图11所示。计算流线上各点处的二阶导数y″(x),结果如图12所示。
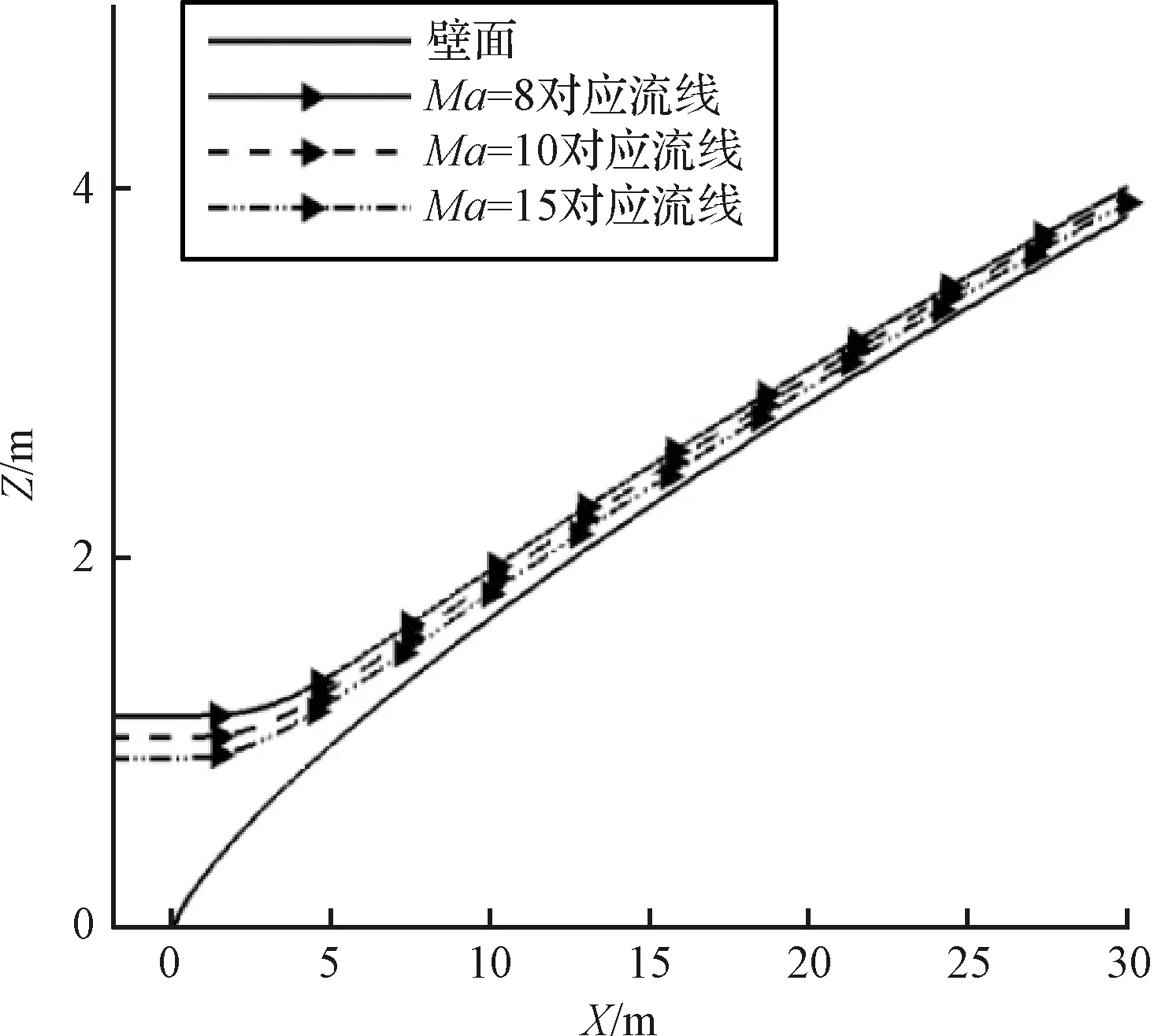
图11 基准流场中的流线Fig.11 Streamlines in the basic flow field
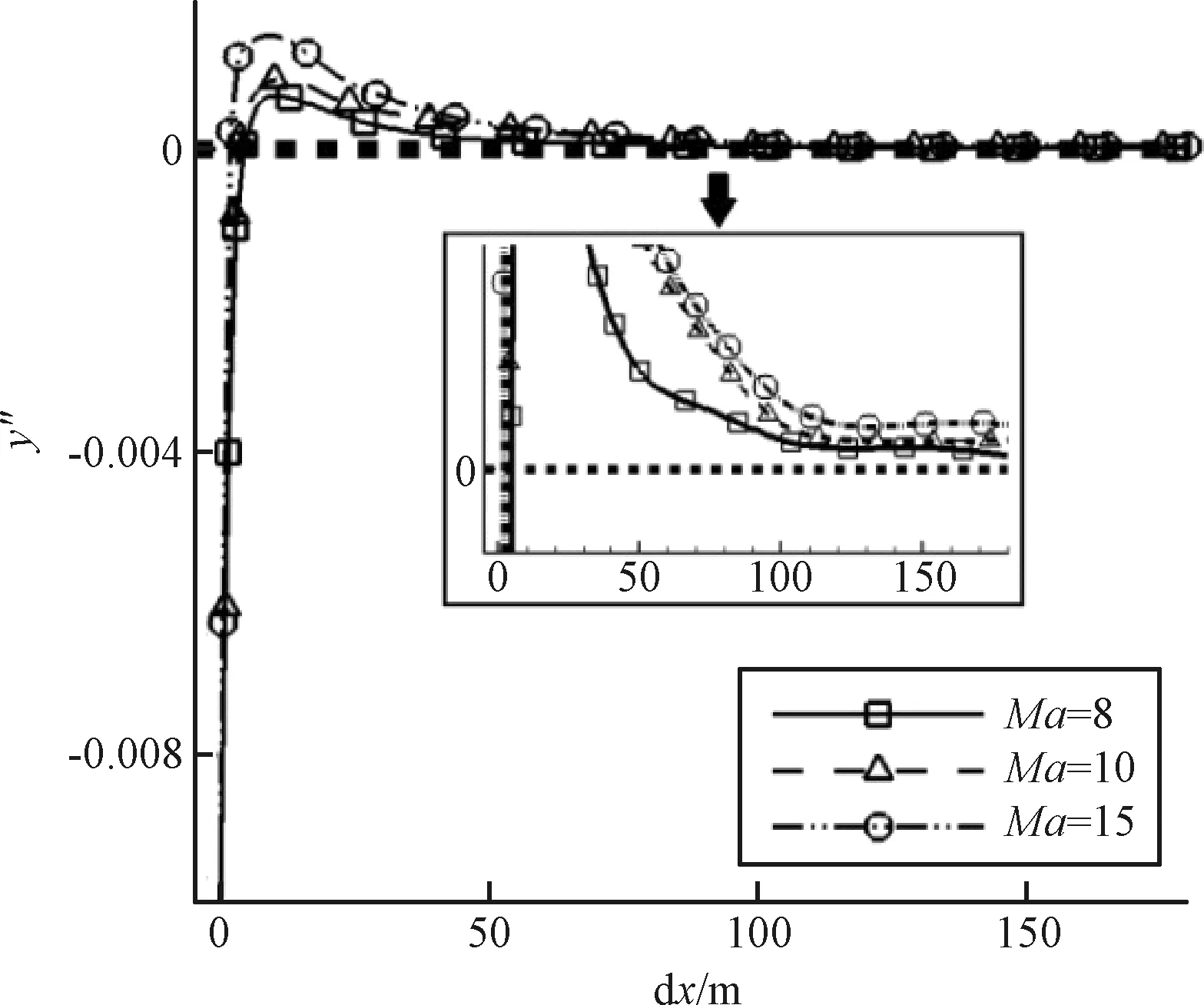
图12 设计马赫数对流线“凹凸”特性的影响Fig.12 Influence of Ma on“concave-convex” characteristics of streamlines
由图12可知,不同流场中流线的“凹凸”特性发生转变的趋势是一致的,但随着设计工况Ma的变化,流线特征分割点与前缘点之间的距离s发生了变化。Ma=8时,s=4.5 m;Ma=10时,s=3.5 m;而Ma=15时,s=2 m。显然,Ma越小,对应流线的特征分割点距前缘点之间的距离s也越大,即流线的“内凹”段越长。其原因在于:随着Ma的减小,激波减弱,基准流场中的激波面与壁面的距离变大,流体要流过更长的距离才能使得壁面的膨胀效应影响足够大,从而导致流线的几何特征发生转变。
由以上分析可知:由于激波压缩效应的影响,乘波体下表面流线在起点(前缘点)处是“内凹”的;而在激波面后由于受到壁面膨胀效应的影响,流线由内凹逐渐转变为“外凸”并保持下去。此外,流线的这一“凹凸”特性与幂次乘波体的设计参数c,n,设计Ma以及前缘点的位置密切相关。参数c越大、n越小、Ma越大、前缘点越靠前,则流线的特征转换点就越靠后,“内凹”段就越长。
文献[13]指出:“外凸”型流线有利于乘波体的纵向静稳定,而“内凹”型流线不利于乘波体的纵向静稳定;且随着乘波体下表面流线“外凸”部分比例的增加,乘波体纵向也就越稳定,当“外凸”成为主导特征时,乘波体纵向静稳定。因此,结合第2节的分析结果可知,那些能够使流线“凹凸”特征转换提前,缩短流线“内凹”段的因素也将利于乘波体的纵向静稳定性,即参数c越大、n越小、设计Ma越大以及前缘点位置越靠前,则乘波体纵向也就越稳定。此外,在流线“内凹”段长度不变的情况下,通过增加乘波体的长度来增加流线“外凸”段的长度也能够促使乘波体纵向静稳定。
3 设计参数对幂次乘波体纵向静稳定性影响
在飞行器设计的初始阶段,由于质心位置未知,工程中一般采用计算纵向压心系数随攻角的变化趋势(即Xcp-α曲线)来判断飞行器的纵向静稳定性。如果攻角增大,压心后移可以为飞行器提供低头力矩,此时飞行器是纵向静稳定的;而如果随着攻角的增加,压心前移则会使飞行器产生抬头力矩,此时飞行器纵向静不稳定。因此,本节采用纵向压心系数随攻角的变化趋势来对乘波体的纵向静稳定性进行判断。
3.1 数值方法校验
在进行乘波体纵向静稳定性计算之前,本节以文献[15]给出的典型高超声速升力体——三维Ames All-body模型的试验结果为例,对所采用的数值模拟方法在计算高超声速问题上的可靠性进行校验。图13对比了通过CFD数值模拟和试验获得的不同攻角下模型迎风面和背风面中心线上的压力分布。由图13可知,在迎风面和背风面,二者压力都吻合较好,该结果表明本文采用的CFD求解方法在评估高超声速飞行器的气动力特性时是可靠的。

图13 模型中心线上的压力分布Fig.13 Pressure distribution on the centre line of the model
3.2 长度对幂次乘波体纵向静稳定性影响
设定幂函数曲线参数Lb=185 m,n=0.75,c=0.3,在设计工况Ma=10的流场中生成幂次体基准流场。并在Lb=185 m的投影面上取前缘线的投影方程为y=-3.41-0.1z。在最终得到的乘波体上横切出长度分别为100 m,60 m以及20 m的幂次乘波体。图14是不同长度乘波体的纵向压心系数随攻角的变化曲线。

图14 乘波体长度L对Xcp的影响Fig.14 Influence of L on Xcp
由图14可知,L=20 m和60 m时,乘波体纵向压心系数随攻角增大而减小,曲线斜率小于0,乘波体纵向静不稳定。且乘波体长度为60 m时,乘波体的纵向压心系数斜率更大一些,乘波体稳定性得到提高。而长度为100 m时,乘波体纵向压心系数随攻角增大而增大,曲线斜率大于0,乘波体达到纵向静稳定。
由以上计算结果可以发现:乘波体的长度越长,其纵向也就越稳定。该结论与第2节的分析结果是一致的,即在其他参数不变的情形下,乘波体长度的增加直接导致了其下表面流线“外凸”段的增加,因此乘波体的纵向静稳定性也会更好。
3.3 前缘线与对称面交点位置对幂次乘波体纵向静稳定性影响
前缘投影线与对称面交点位置直接影响了整个生成乘波体的下表面流线在源流场的起点位置,交点距投影面中心距离越大说明起点(即该条流线上的前缘点)越靠后。设定幂函数曲线参数Lb=185 m,n=0.75,c=0.3,在设计工况Ma=10的流场中生成幂次体基准流场。在Lb=185 m投影面上取三条不同的投影曲线y=-2.92-0.1z,y=-3.41-0.1z和y=-5.44-0.1z,其对应的乘波体下表面流线起点距幂次体头部横坐标距离dx0分别为24 m,60 m和100 m。由以上信息生成乘波体并截取相同的长度L=70 m。图15是不同乘波体压心系数随攻角的变化曲线。
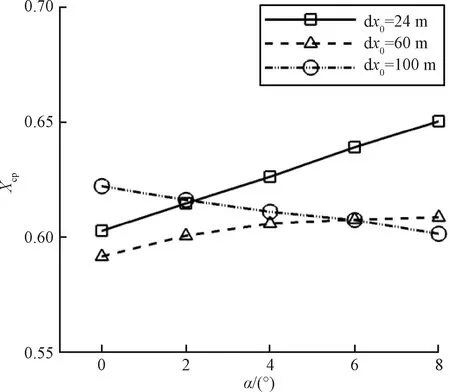
图15 交点位置对纵向压心系数Xcp的影响Fig.15 Influence of intersection position on Xcp
由图15可知,x0=24 m和60 m时,乘波体纵向压心系数随攻角的增大而增大,曲线斜率大于0,乘波体纵向静稳定。且x0=24 m时,对应的曲线斜率更大,乘波体的稳定性得到进一步提高;当x0=100 m 时,乘波体纵向压心系数随攻角的增大而减小,曲线斜率小于0,乘波体纵向静不稳定。
由以上计算结果可以发现,前缘线投影线与对称面的交点距投影面中心的距离越小,即乘波体下表面流线的起点越靠前,乘波体纵向越稳定。该现象与第2节分析结论一致,即乘波体前缘点越靠前,流线的特征分割点就越靠前,乘波体下表面流线的“内凹”段缩短,“外凸”部分比例增加,乘波体纵向也就越稳定。
3.4 前缘线形状对幂次乘波体纵向静稳定性影响
在固定的源流场中,前缘线形状将直接决定乘波体下表面几何特征及其气动力特性,因此本节在保证其他研究参数一致的情形下对前缘线形状与乘波体纵向静稳定性之间的关系展开研究。设定幂函数曲线参数Lb=185 m,n=0.75,c=0.3,在设计工况Ma=10的流场中生成幂次体基准流场。在保证乘波体前缘线与对称面交点位置相同的情形下,在Lb=185 m的基准面上取五条不同形状的投影曲线y=-11.377-0.00843z2,y=-11.377-0.2z,y=-11.377-0.4z+0.00843z2,y=-11.377-0.5z,y=-11.377-z,投影线依次编号P1~P5,如图16所示。由以上信息生成乘波体并计算其纵向压心系数随攻角的变化趋势,如图17所示。
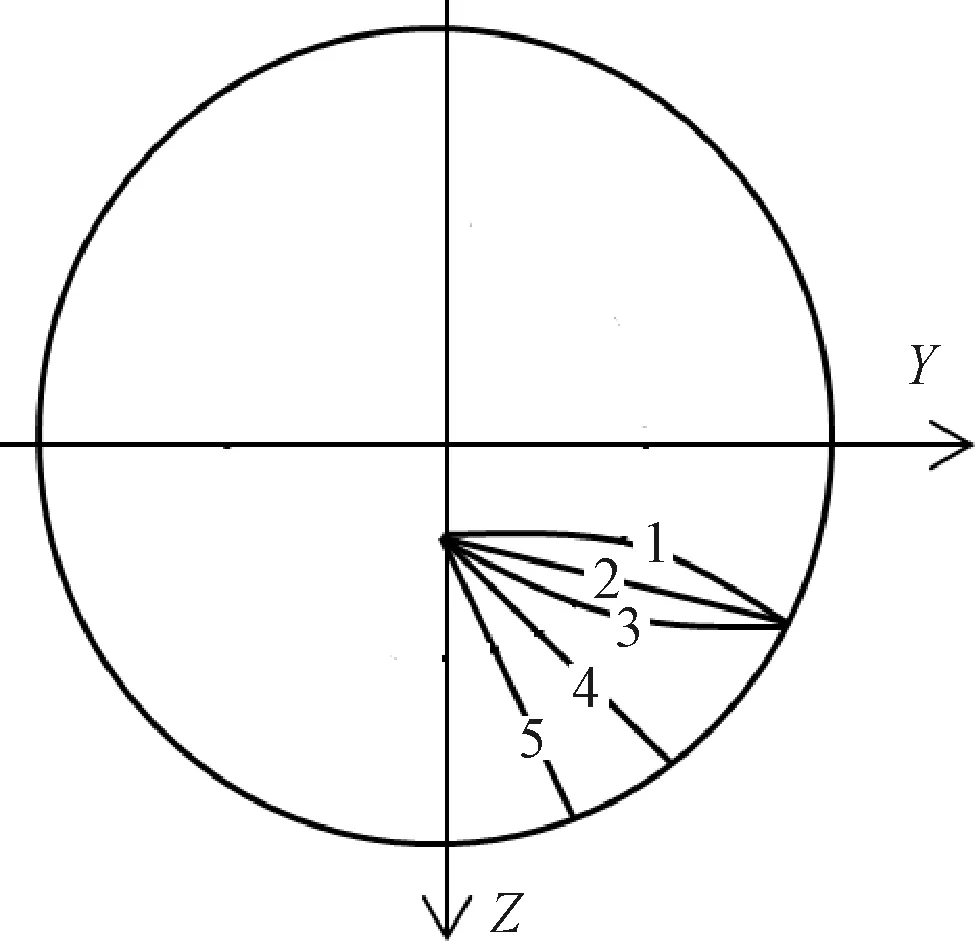
图16 前缘线在基准面上的投影线Fig.16 Projection lines of leading edges on the basic surface

图17 前缘线形状对纵向压心系数Xcp的影响Fig.17 Influence of leading edge shape on Xcp
由以上计算结果可以发现,基准面上前缘投影线的弯曲和斜率并没有对乘波体的纵向静稳定性产生影响,但引起了压心位置的变化。该现象表明前缘线的形状并没有对乘波体的纵向静稳定性产生影响。结合第2.2.1节的结论可对此进行分析,即对于同一源流场中的任两条前缘线,如果它们与乘波体对称面的交点距幂次体头部距离相等,那么沿X轴对源流场进行横切,则横截面与这两条前缘线的交点距幂次体的头部的距离都是相等的。在不考虑径向流动的情况下,由于幂次体流场的轴对称性,结合第2.2.1节的分析结论可知,以这两个交点作为前缘点追踪得到的流线“凹凸”特征也必然是一致的。进而将该结论扩展到整条前缘线上就可以得到这样的结论:在同一源流场中,如果两条前缘线与乘波体对称面的交点距幂次体头部距离相等,那么由此两条前缘线生成的乘波体其纵向静稳定性也是一致的。
3.5 参数c对幂次乘波体纵向静稳定性影响
设定幂函数曲线参数Lb=185 m,n=0.75,c=0.2,0.3,0.7,在设计工况Ma=10的流场中生成三个不同的幂次体基准流场。由第3.3和3.4节的分析可知,乘波体的纵向静稳定性与前缘线形状无关,而与前缘线和对称面的交点位置有关。因此,本文在对参数c的研究中,为了使不同源流场中乘波体前缘线与对称面的交点距幂次体头部距离相等,将基准面上前缘投影线分别取为:y=-2.72-0.1z,y=-3.41-0.1z以及y=-6.43-0.1z,生成乘波体。

图18 参数c对Xcp的影响Fig.18 Influence of parameter c on Xcp
图18是不同乘波体纵向压心系数随攻角变化曲线。由图18可知,参数c=0.2和c=0.3时,对应的乘波体的压心系数随攻角的增大而减小,乘波体纵向静不稳定;并且c=0.2时,对应曲线的斜率更小,其纵向静稳定性也更差;当参数c=0.7时,对应乘波体的纵向压心系数随攻角增大而增大,曲线斜率大于0,乘波体纵向静稳定。
从以上计算结果可以发现,随着参数c的增加,乘波体的纵向静稳定性也就越好。该现象与第2节分析结果一致,即随着参数c的增加,乘波体下表面流线的特征分割点距前缘点的距离变小,流线的“内凹”段缩短,“外凸”段比例增加,乘波体的纵向静稳定性也就更好。
3.6 参数n对幂次乘波体纵向静稳定性影响
设定幂函数曲线参数Lb=185 m,c=0.3,n=0.6,0.75,0.9,在设计工况Ma=10的流场中生成三个不同的幂次体基准流场。由第3.3节和3.4节的分析可知,乘波体的纵向静稳定性与前缘线形状无关,而与前缘线和对称面交点位置有关。因此,本文在对参数n的研究中,为了使不同源流场中乘波体前缘线与对称面的交点距幂次体头部距离相等,将基准面上前缘投影线分别取为y=-3.12-0.1z,y=-3.41-0.1z和y=-4.13-0.1z,生成乘波体。图19是不同乘波体纵向压心系数随攻角变化曲线。

图19 参数n对Xcp的影响Fig.19 Influence of parameter n on Xcp
由图19可知,参数n=0.9以及n=0.75时,乘波体压心系数随攻角的增大而减小,斜率小于0,乘波体纵向静不稳定;且n=0.9时,对应乘波体的纵向压心系数斜率更小,稳定性更差;参数n=0.6时,对应乘波体的压心系数随攻角的增大而增大,乘波体纵向静稳定。
从以上计算结果可以发现,随着参数n的减小,乘波体的纵向静稳定性逐渐提高。该结论与第2节分析结果一致,即随着参数n的减小,乘波体下表面流线的特征转变提前,流线“内凹”段缩短,“外凸”段比例增加,乘波体纵向也就更稳定。
3.7 设计马赫数对幂次乘波体纵向静稳定性影响
设定幂函数曲线参数Lb=185 m,c=0.3,n=0.75,在设计工况Ma=8,10和15的流场中生成三个不同的幂次体基准流场。由第3.3节和3.4节的分析可知,乘波体的纵向静稳定性与前缘线形状无关,而与前缘线和对称面交点位置有关。因此,本文在对设计Ma的研究中,为了使不同源流场中乘波体前缘线与对称面的交点距幂次体头部距离相等,将基准面上前缘投影线分别取为y=-5.66-0.1z,y=-3.41-0.1z和y=-2.47-0.1z生成乘波体。图20是不同乘波体的纵向压心系数随攻角变化曲线。
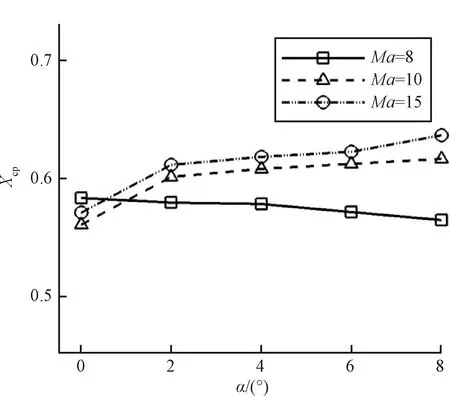
图20 设计Ma对Xcp的影响Fig.20 Influence of Ma on Xcp
从图20可以看出,Ma=8时,对应乘波体的纵向压心系数随攻角的增大而减小,曲线斜率小于0,乘波体纵向静不稳定;Ma=10和15时,乘波体的纵向压心系数随攻角的增大而增大,曲线斜率大于0,乘波体纵向静稳定;并且,Ma=15时,对应曲线斜率更大,乘波体的纵向静稳定性也更好。
从以上计算结果可以发现,随着设计Ma的增大,乘波体的纵向静稳定性越来越好。该结论与第2节分析结果一致,即在其他设计参数不变的情形下,随着设计马赫数的增大,乘波体下表面流线的特征分割点前移,“内凹”段缩短,“外凸”段比例增加,乘波体在纵向也就变得越来越稳定。
4 结 论
本文通过数值计算的方法研究了幂次乘波体下表面流线的凹凸特性与设计参数之间的关系,进而以此为依据分析了设计参数与乘波体纵向静稳定性之间的关系,具体结论如下:
1)由于受到激波压缩效应和壁面膨胀效应的影响,激波面后流线在激波面附近表现为“内凹”,而在流线的特征分割点处转变为“外凸”,并随着流动的进行保持“外凸”。
2)流线的“凹凸”特性与设计参数c,n,Ma以及前缘点位置密切相关;虽然参数的改变不会对流线前“凹”后“凸”这一整体特征产生影响,但参数c越大、n越小、设计Ma越大、前缘点设置的越靠前,流线的特征转变就越早,“内凹”段也就越短。
3)幂次乘波体的纵向静稳定性与设计参数c和n、乘波体长度L、设计Ma以及前缘点的位置有关,且c越大、n越小、L越长、设计Ma越大、前缘点位置越靠前则幂次乘波体纵向越稳定。此外,在其他设计参数确定的情形下,前缘线形状的改变不会对幂次乘波体的纵向静稳定性产生影响。
需要注意的是,文中为了凸显设计参数对乘波体纵向静稳定的影响,并没有讨论乘波体的升阻比和容积率的变化,后续工作中将予以考虑,并以纵向静稳定性、升阻比和容积率共同作为设计目标进行幂次乘波体的优化设计。
