火箭整流罩声振环境缩比特性研究
2019-09-05荣吉利范博超程修妍谌相宇
荣吉利,范博超,程修妍,谌相宇
(1. 北京理工大学宇航学院,北京 100081;2. 中国工程物理研究院电子工程研究所,绵阳 621900)
0 引 言
运载火箭在飞行过程中主要受到气动噪声[1]和喷流噪声的影响,由燃气射流引发的气动噪声可达到160 dB以上[2]。外部噪声以宽频、随机的形式通过透射和辐射传递到整流罩内部[3],直接影响到有效载荷的可靠性,甚至导致整个任务失败,发生灾难性的事故[4-5]。因此整流罩声振环境的研究是不可或缺的一项重要内容。
目前,对整流罩声振环境的研究主要采用数值仿真和试验测量两种方法。工程中采用的数值仿真方法主要有:有限元方法(Finite element method,FEM)、边界元方法(Boundary element method,BEM)和统计能量分析方法(Statistical energy analysis,SEA)。韩峰等[6]采用FEM/BEM方法,对航天飞行器中的圆锥壳结构进行了声振耦合仿真计算,并与试验进行了对比,仿真曲线的最大峰值与试验测量相差在2 dB之内。杜骊刚[7]采用NASTRAN对某飞行器在噪声环境下的振动响应进行了预示并与噪声试验作了对比,主要测点总均方根误差在6 dB以内,验证了使用三维有限元模型进行振动环境预示方法的有效性。韩增尧等[8]对卫星太阳翼在噪声环境下的加速度响应进行了详细研究,利用SEA法对太阳翼的声振力学环境进行了预示,并通过与试验结果对比,验证了上述方法的可行性。Pirk等[9]采用了SEA方法研究运载火箭声振模型,并由此开展了噪声控制研究。采用混合FEM-SEA法,朱卫红等[10]建立了航天器声振预示模型,预示了航天器全频段声振环境,通过试验对比验证了预示方法和模型的有效性。
由于全尺寸试验成本高、难度大且不易于快速测量试验数据,缩比模型试验作为取代全尺寸试验的一种重要手段得到广泛应用。陈劲松等[11]提出了模拟火箭发射初期燃气喷流缩比试验的5个基本相似参数:线性几何尺寸比、燃烧室压强、环境压强、燃气比热比、燃气火药力,在满足这5个相似参数的情况下,缩比模型试验的燃气流场结构与原型试验的燃气流场结构保持线性几何相似关系。Doug等[12-13]在预示Ares I火箭起飞噪声环境、点火超压环境时应用缩比模型噪声试验方法得到了较好的结果。Morgan等[14]将火箭发动机缩比模型进行了简化,用简化后的缩比模型试验获得了发动机近场噪声,但其误差较大。任方等[15]基于相似理论,根据几何相似、喷流参数相似、发射环境相似来预示起飞噪声环境,得到了运载火箭表面噪声环境的空间相关特性。以上方法均未通过理论分析和仿真校验的角度为飞行状态下整流罩缩比试验进行指导。
本文基于量纲分析进行了火箭飞行过程中整流罩声振环境的缩比特性研究,推导并获得了不同缩比模型与全尺寸模型之间内部声场、壁面振动加速度的关系,使用有限元方法进行了仿真计算,校验了缩比准则的正确性。因此,在声振环境试验中可参考本文的缩比准则设计缩比模型试验。
1 理论分析
1.1 有限元声振耦合理论
声学有限元方法可以同时考虑内外声场并建立结构与内外声场耦合的模型。具体而言,首先对结构建立有限元结构离散方程,对声场建立有限元声学系统方程,然后考虑声振耦合面的相互作用,并在结构有限元动力学方程中加入声场对结构的作用项,在声学系统方程中加入结构对声场的作用项,联立方程就可以建立起结构与内外声场耦合的动力学方程[16]:
(1)
式中:Ks,Cs和Ms分别为结构有限元的刚度矩阵、阻尼矩阵和质量矩阵;ρ0为声学介质密度;ω为角速度;Kc为声学介质与结构耦合刚度矩阵;Ka,Ca和Ma分别为声学有限元的刚度矩阵、阻尼矩阵和质量矩阵;u与p分别为结构位移向量与声压向量;Fs与Fa分别为外载荷与声载荷激励向量。
1.2 量纲分析
噪声是随机声环境,以声谱、声压级、空间相关等参数描述。远场声功率与声压的关系式为:
(2)
式中:W为声功率;R为声波传播的半径;ρ0c0为介质的特性抗阻。
因此,决定整流罩内部声压强度特征的控制参数来自以下3个方面:
1)声源参数:声功率W,振动频率f,声源到整流罩内部的距离R。
2)介质参数:密度ρ0,声音在介质中的传播速度c0。
3) 结构参数:密度ρs,弹性模量Es,泊松比νs,厚度hs,阻尼比ζ。
于是,整流罩内部声压p是上述控制参数的函数:
p=F(W,R,f;ρ0,c0;ρs,Es,νs,hs,ζ)
(3)
取ρ0,c0和W作为基本量,式(3)可转化为下面的无量纲关系:
(4)
如果缩比模型与原模型声学介质参数相同,且结构材料相同,则6个有关参数与原模型保持相同,即
(ρ0,c0;ρs,Es,νs,ζ)=const
(5)
则式(4)可简化为
(6)
根据相似律,若要使整流罩缩比模型内声场psca与原模型p相等,则要满足:
(7)
由式(5)可知,式(7)简化后为:
(8)
式中:下角标sca表示缩比模型参数。
通过上述分析可知,假设声源声功率W的缩比比例为Wsca/W=α2,振动频率变为fsca=(1/α)f,声源到整流罩内部的距离Rsca=αR,结构厚度变为hs,sca=αhs,则缩比模型与原模型的内声场相同。
同理,整流罩壁面振动加速度是式(3)中控制参数的函数,简化后的无量纲式为
(9)
根据相似律:
(10)
即当声功率W的缩比比例为α2时,缩比模型整流罩的壁面振动加速度asca=(1/α)a。
2 仿真校验
2.1 仿真模型
参考某火箭整流罩的结构,使用Virtual.lab软件建立了如图1所示的整流罩有限元模型。壁面结构模型为蒙皮,为三角形壳单元。声学模型包括外部包络网格和内部声腔网格,均为四面体声学网格,外部包络网格的外表面定义为自适应匹配(AML)层,原模型的结构网格量为8536,声学网格量为308401。

图1 整流罩有限元模型Fig.1 The finite element model of the fairing
在整流罩地面噪声试验中,通常将整流罩放置于混响室,采用扬声器作为声源激励来产生高声压级的外噪声环境,并采用麦克风获取整流罩内外的声压数据。参照混响试验条件,在声学仿真中采用24个分布式平面波模拟试验条件下的混响环境,这24个平面波均布在以整流罩为中心的球面上,如图2所示。将整流罩与空气接触位置的结构网格和声网格定义声振耦合关系,采用基于结构模态的声振耦合算法计算内声腔的响应和整流罩的壁面振动。

图2 分布式平面波示意图Fig.2 Schematic diagram of distributed acoustic plane wave
由式(8)可知,当缩比模型的缩比比例为α时,声源声功率应变为原模型的α2倍,振动频率变为1/α,整流罩的厚度变为α倍,声源到整流罩内部的距离变为α倍。由相似律,计算频率与振动频率缩比比例相同,因此计算频率范围同样变为1/α倍。整流罩的材料属性为铝,其密度为2700kg/m3,弹性模量70 GPa,泊松比0.3,阻尼比2%;将空气简化为理想媒介,声波在其中传播时不存在耗散,空气声速和密度分别设为346 m/s,1.185 kg/m3,在本文计算中均采用此参数。参照原模型,本文分别建立了1/2,1/3,1/4,1/5缩比比例的模型来分析对比。计算了原模型与缩比模型的内声腔的响应和整流罩的壁面振动,其频率范围分别为10~300 Hz,20~600 Hz,30~900 Hz,40~1200 Hz和50~1500 Hz。
2.2 结果与对比
由于有效载荷通常位于整流罩圆柱段,建立图3所示的场点网格来获得整流罩内声腔的声压级响应,长方形场点网格均匀分布在圆柱段内,由25个单元36个节点组成。对于缩比模型,其场点网格成比例缩小。

图3 场点分布示意图Fig.3 Schematic diagram of field points distribution
采用声学有限元方法计算得出了原模型与缩比模型的场点声压级,使用声压均方根平均法将24个平面波激励下的场点声压响应进行叠加,得到在混响激励下的场点声压级。图4为原模型与缩比模型的场点平均声压级曲线,图5为场点峰值声压级曲线。由于原模型与缩比模型的计算频率与圆柱段直径的乘积是不变的,为便于对比,采用此方式来分析原模型与缩比模型的差异。声压均方根平均法的计算公式[17]为
(11)
式中:Li为场点的声压级,n为场点节点数。

图4 场点平均声压级Fig.4 Average sound pressure level of field points

图5 场点峰值声压级Fig.5 Peak sound pressure level of filed points

表1 原模型与缩比模型平均声压级对比Table 1 Comparison of average sound pressure level between the original model and the scaling models
为了定量地校验缩比准则结果,以原模型为参考,分别取频率为50 Hz,100 Hz,150 Hz,200 Hz,250 Hz处的场点声压级进行对比分析。式(8)表明,缩比模型整流罩内部场点声压级与原模型一致。表1表2为原模型与缩比模型的平均声压级、峰值声压级对比表,且给出了偏差值。

表2 原模型与缩比模型峰值声压级对比Table 2 Comparison of peak sound pressure level between the original model and the scaling models
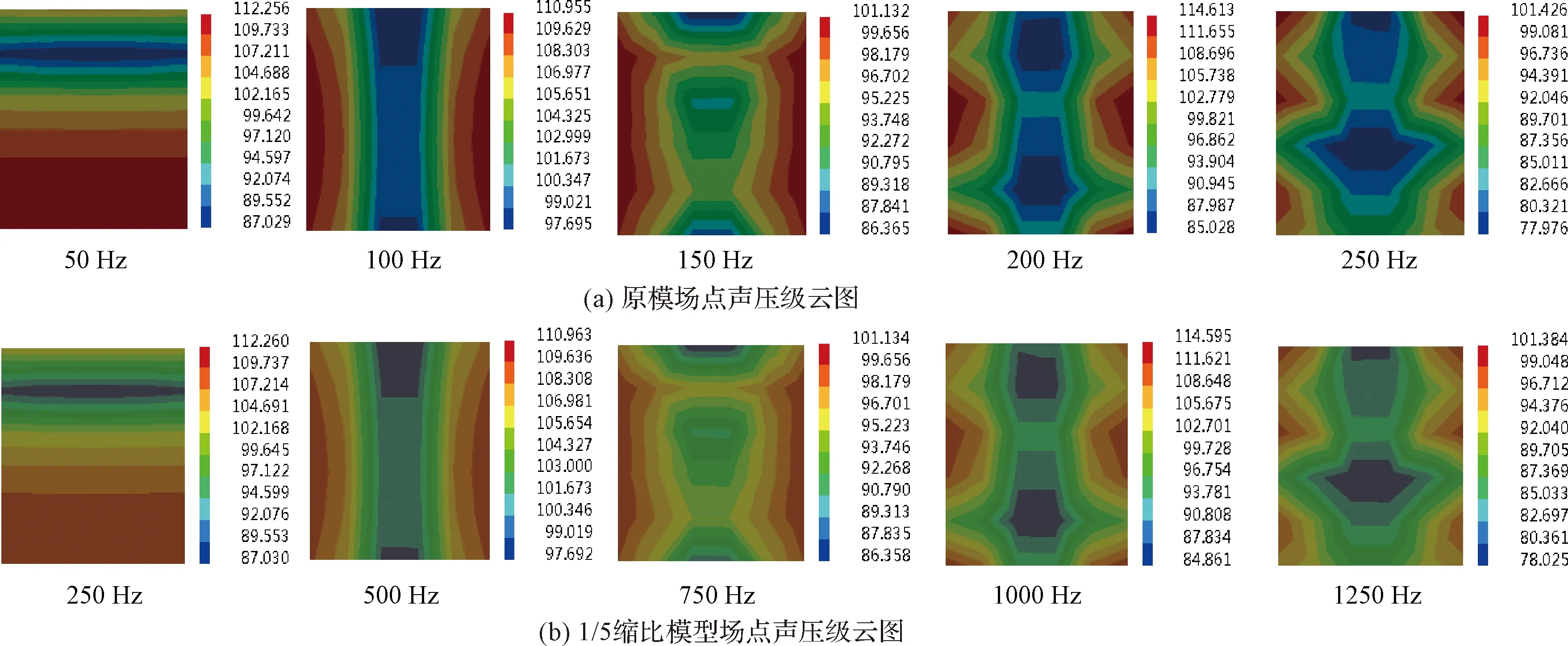
图6 原模型与1/5缩比模型场点声压级云图对比Fig.6 Comparison between sound pressure level of the original model and sound pressure level of the 1/5 scaling model
从表1、表2可以看出,原模型与缩比模型平均声压级在对应频率上相同,最大相差0.04 dB,而峰值声压级最大相差0.09 dB。图6为原模型与1/5缩比模型的场点声压级云图对比,原模型与缩比模型在对应频率上声压级分布相同,只在数值上有微小差别,校验了缩比准则在声压级上的正确性。

图7 整流罩样本点位置Fig.7 The position of sample points
由于整流罩的呼吸变形对有效载荷的包络空间影响较大[18],选取了图7所示整流罩纵向对称面上的一系列样本点,使用均方根平均法将24个平面波激励下的样本点径向加速度响应进行叠加,得到混响激励下样本点的径向加速度,研究整流罩结构上的振动情况是否满足相似准则。获得了原模型与缩比模型的径向平均加速度曲线(见图8),图9为径向峰值加速度曲线。
同样以原模型为参考,分别取频率为50 Hz,100 Hz,150 Hz,200 Hz,250 Hz处样本点径向加速度进行分析对比。由式(10)可知,当缩比比例为α时,缩比模型整流罩壁面振动加速度为原模型1/α。表3、表4为原模型与缩比模型样本点径向平均加速度、峰值加速度对比表,误差的计算公式为
|asca·α-a|/a
(12)

图8 样本点径向平均加速度Fig.8 Average acceleration of sample points
从表3、表4可以看出,当缩比比例为α时,缩比模型与原模型样本点径向加速度在对应频率上为1/α,样本点径向平均加速度最大误差为0.98%,峰值加速度最大误差为1.28%,在网格划分等因素造成的误差之内。图10为原模型与1/5缩比模型的加速度云图对比,可以看出缩比模型与原模型在对应频率上加速度分布相同,缩比模型加速度为原模型的5倍,与理论分析所得的缩比特性一致。

图9 样本点径向峰值加速度Fig.9 Peak acceleration of sample points

表3 原模型与缩比模型样本点径向平均加速度对比Table 3 Comparison of average acceleration at the field point between the original model and the scaling models
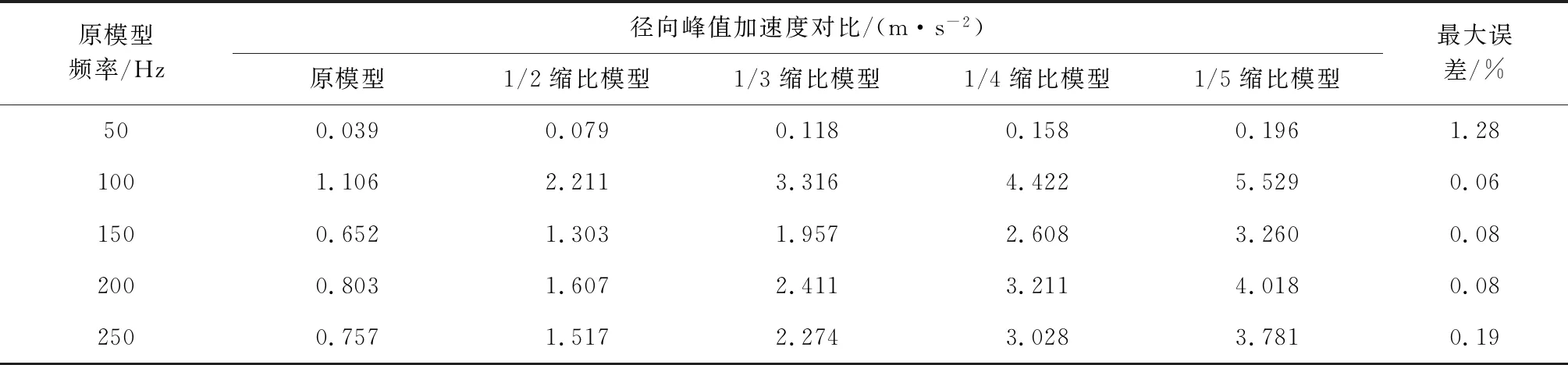
表4 原模型与缩比模型样本点径向峰值加速度对比Table 4 Comparison of peak acceleration at the field point between the original model and the scaling models
在仿真计算的过程中,虽然缩比模型尺寸较小,但其计算频率范围更广,而计算频率上限又与线性网格单元尺寸有对应关系[19]:
(13)
式中:L为单元长度,c0为声音在介质中的传播速度,fmax为最高计算频率。
因此为了获得较大的计算频率上限,缩比模型的单元尺寸更小,从而网格数量与原模型相同。对于缩比模型的计算频率范围更广的情况,增大计算频率间隔从而使计算步数相同。由于缩比模型与原模型网格数量、计算步数相同,因此仿真时间也几乎相同,从而在仿真中使用缩比模型并不能提高计算效率。但在声振环境试验中可以参考本文的缩比准

图10 原模型加速度云图与1/5缩比模型加速度云图对比Fig.10 Comparison between acceleration of the original model and acceleration of the 1/5 scaling model
则设计缩比模型试验。
3 结 论
以某火箭整流罩为研究对象,通过量纲分析以及声学有限元仿真对不同缩比比例下整流罩内声场、壁面振动加速度进行了研究,得出了缩比模型与原模型的比例关系,形成缩比准则,即在α2倍声功率下,缩比模型内声场与原模型一致,整流罩壁面加速度为原模型的1/α。结果表明,缩比模型与原模型保持较高的相似性,本文所推导的相似关系可以应用到声振环境预示、声振环境试验中。
理论上讲参考本文的缩比准则可设计任何缩比比例下缩比模型试验,缩比倍数越大越节省费用,但在实际试验过程中,缩比倍数越大,声压在单位尺度上的变化率越高,这将对试验测试造成困难,增大试验误差,而且随着缩比倍数增大,整流罩厚度越薄,一方面不利于加工制造,另一方面可能会使材料的强度等参数发生变化,因此在实际缩比试验中应当合理选择缩比比例。
