超静超稳卫星碰振动力学建模

杨鸿杰，刘 磊，李新国，赵艳彬

(1. 西北工业大学航天学院，西安 710072；2. 陕西省空天飞行器设计重点实验室，西安 710072；3. 上海卫星工程研究所，上海 200240)

0 引 言

随着航天技术的发展，航天器敏感载荷对指向精度和指向稳定度提出了越来越高的要求[1-3]。为了满足航天器敏感载荷高精度高稳定度指向需求，多种主动和被动振动隔离技术已经在航天器上得到应用[4]。Pedreiro[5]提出了一种新型航天器结构，称之为分离式卫星(Disturbance-free payload, DFP)。分离式卫星将传统卫星模块化分解为载荷模块(Payload module, PM)和服务模块(Support module, SM)。具有高精度和高稳定度指向需求的敏感载荷如空间望远镜等，可视为载荷模块。卫星平台可视为服务模块，服务模块包含了卫星的姿态控制系统，供电系统和热控系统等。载荷模块的位置和姿态控制通过非接触作动器实现，理论上分离式卫星载荷模块可完全隔离服务模块的振动，隔振频率接近0 Hz，并且隔振能力不受到传感器和作动器性能限制。上海卫星工程研究所也设计了无刚性连接结构的超静超稳双超卫星平台，用于实现载荷模块和卫星平台动静隔离、主从协同控制[6]。

分离式卫星是一种结构简单，工程上容易实现的超静超稳航天器技术，文献[7-10]开发了分离式卫星仿真模型和地面模拟系统，并进行了3次地面试验。地面试验测试了分离式卫星含/不含柔性线缆情况下的隔振性能和敏捷机动能力，试验结果表明，分离式卫星载荷模块在0.01～100 Hz内对服务模块的振动隔离效率达到60 dB，且载荷模块可实现角加速度为14 (°)/s2姿态机动。Wu等[11]研究了音圈电机反电动势和柔性线缆对分离式卫星载荷模块六自由度控制带来的耦合问题。Xu等[12]建立了音圈电机立方体安装构型下分离式卫星动力学模型，并研究了载荷模块姿态鲁棒控制问题。庞岩等[13]建立了柔性线缆连接下分离式卫星载荷模块动力学模型，并仿真分析了柔性线缆对载荷模块指向精度和指向稳定度的影响。孔宪仁等[14]建立了分离式卫星载荷模块和服务模块近距离相对运动的动力学模型。

综上所述，对于分离式卫星载荷模块动力学建模和控制已经有了大量研究，但很少有文章研究分离式卫星两模块碰撞问题。Pedreiro在提出分离式卫星构型时指出，分离式卫星面临的一个技术挑战就是如何避免载荷模块和服务模块之间发生碰撞，例如分离式卫星载荷模块在锁紧释放后可能具有一定的初始速度，或在运行过程中受到扰动，都可能导致两模块发生碰撞。对于航天器碰撞问题已经有了较为深入的研究[15-17]，如空间机器人捕获目标过程中的碰撞问题以及空间可展开机构中存在的间隙碰撞问题等，但这些碰撞模型不适用于分离式卫星接触碰撞过程。

本文综合音圈电机反电动势和柔性线缆动力学的影响，通过牛顿欧拉法建立了分离式卫星载荷模块动力学模型。基于Hertz接触理论，建立了分离式卫星在接触碰撞过程中连续接触力模型，并通过数值仿真分析了碰撞过程中产生的接触力对载荷模块指向精度和指向稳定度的影响。

1 分离式卫星动力学模型

1.1 分离式卫星坐标系统

分离式卫星载荷模块和服务模块之间通过柔性线缆连接，以进行能量供应和数据传输。载荷模块的位置和姿态通过非接触作动器进行控制，非接触作动器一端和服务模块相连，另一端和载荷模块相连。分离式卫星的基本结构如图1所示。

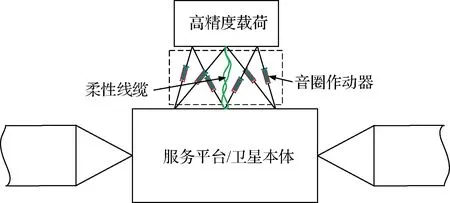
图1 分离式卫星结构示意图Fig.1 Sketch of the DFP

分离式卫星载荷模块和服务模块之间非接触作动器可有多种安装构型，选择非接触作动器安装构型时需要合理考虑作动杆之间相互耦合问题。为建立分离式卫星动力学模型，建立如图2所示的坐标系。

图2中，O-XYZ是惯性坐标系；S-XYZ和P-XYZ分别是服务模块和载荷模块本体坐标系，坐标原点位于两模块质心处；为方便坐标转换，假设分离式卫星处于标称位置时，O-XYZ,S-XYZ和P-XYZ三个坐标系平行。rp和rs分别是载荷模块和服务模块质心在惯性系下矢量；Ai和Bi分别是第i个非接触作动器在载荷模块和服务模块本体坐标系下安装点；li是第i个非接触作动器在惯性系下的方向向量。

分离式卫星运动可视为绕地球转动和偏离标称位置运动的合成。与碰撞过程相比，整星绕地球转动周期长，转动速度较小，因此在推导分离式卫星碰撞动力学时忽略绕地球转动，将轨道坐标系近似认为是惯性坐标系。

1.2 分离式卫星动力学建模

如图2所示，分离式卫星载荷模块的牛顿欧拉方程可由式(1)表示:

(1)

式中：Mp,Ip分别是载荷模块的质量矩阵和转动惯量矩阵；Fd,Td是载荷模块受到的扰动力和扰动力矩，fpi是第i个作动器的主动输出力；ωp是载荷模块相对惯性系转动角速度。

分离式卫星载荷模块受到的扰动力和力矩一部分源于空间环境，另一部分因柔性线缆的存在，导致服务模块的扰动传递到载荷模块。假设柔性线缆在载荷模块和服务模块各自体坐标系下的安装位置矢量分别为pc和sc，则柔性线缆对载荷模块造成的扰动力和扰动力矩可用式(2)和式(3)表示:

(2)

(3)

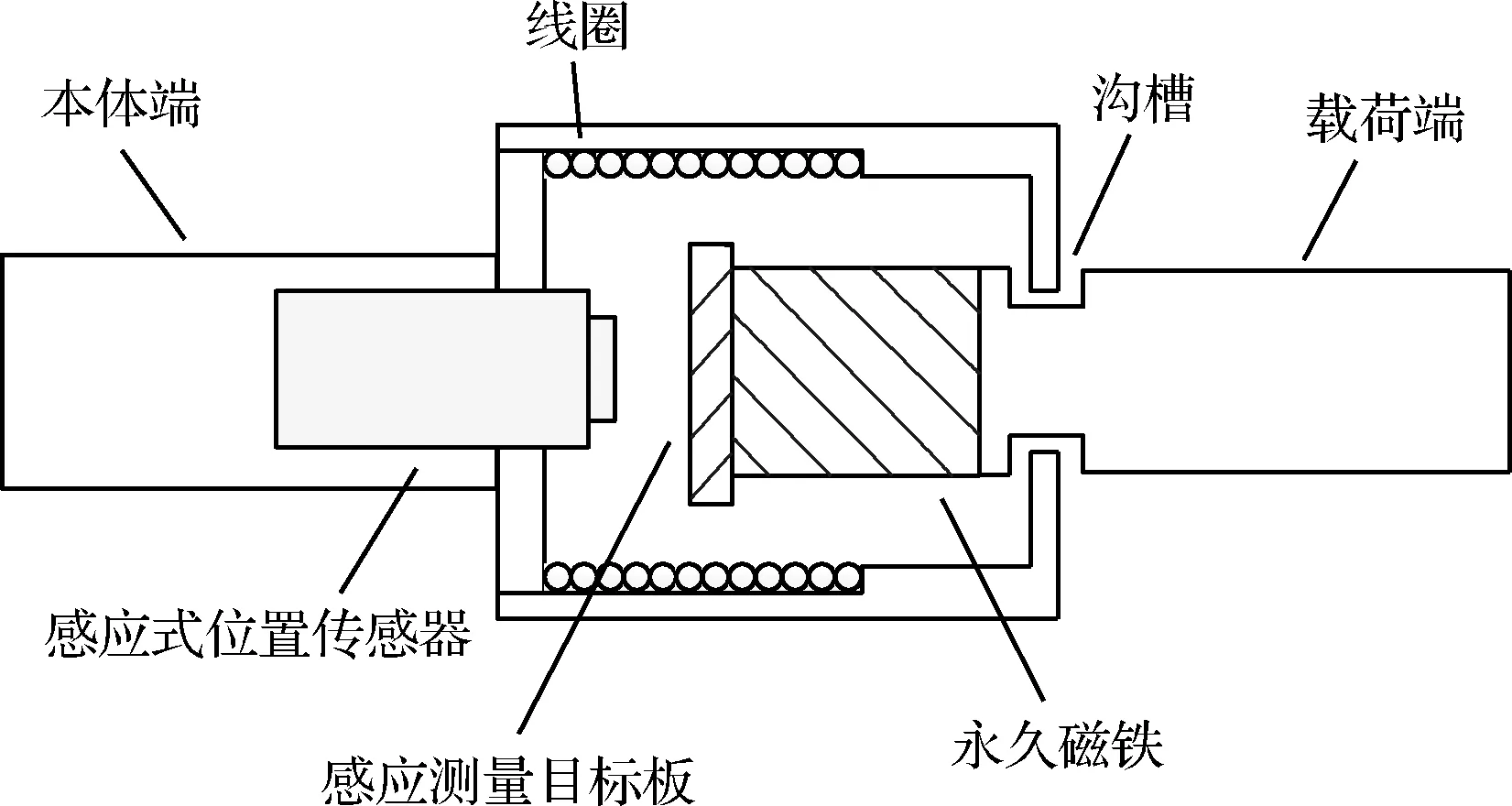
图3 音圈电机结构示意图Fig.3 Sketch of voice coil motor

分离式卫星选用非接触的音圈电机作为执行机构，音圈电机结构如图3所示。音圈电机由载荷端支腿、本体端支腿、永久磁铁和线圈等组成。载荷端支腿设计有沟槽防止载荷模块在工作过程中脱离服务模块。当线圈通电时，载荷端支腿将受到洛伦兹力作用，改变线圈电流大小和电流方向，可改变载荷端支腿受到的作用力大小和方向。

当载荷端支腿和服务端支腿发生相对运动时，线圈在永久磁铁产生的磁场中运动时会产生反电动势，反电动势将产生一个阻尼力，如式(4)所示:[11]

(4)

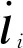
音圈电机支腿相对运动速度与载荷模块和服务模块运动关系如式(5)所示：

(5)

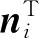
将音圈电机六支腿运动学方程表示成矩阵形式，如式(6)所示：

(6)

定义音圈电机服务模块和载荷模块的安装雅可比矩阵分别为Jp和Js，如式(7)和式(8)所示:

(7)

(8)

六个音圈电机产生的阻尼力可写成如式(9)所示的矩阵形式

(9)

式中：C=diag(cm1, …,cm6)。

根据虚功原理，载荷模块受到广义阻尼力Fdm和阻尼力矩Tdm与音圈电机产生的阻尼力之间的关系满足式(10)[18]

(10)

将式(9)代入式(10)可得式(11):

(11)

将式(2)、式(3)和式(11)代入式(1)可得柔性线缆连接下分离式卫星动力学模型如式(12)和式(13)所示:

(12)

(13)

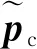
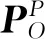
(14)

式中：φ,θ,ψ为载荷模块欧拉角。

将式(14)代入式(12)和式(13)，忽略二阶以上小量，化简可得式(15)：

(15)

式中：

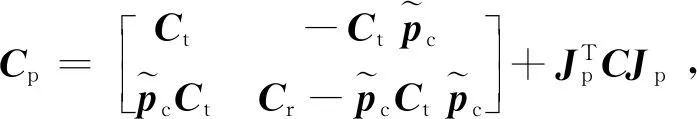
从式(15)可以看出，线性化后分离式卫星载荷模块动力学模型是线性耦合的二阶微分方程组，可用于控制器设计。

2 分离式卫星碰撞建模

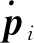
图4 音圈电机碰撞形式ⅠFig.4 Voice coil motor collision form Ⅰ

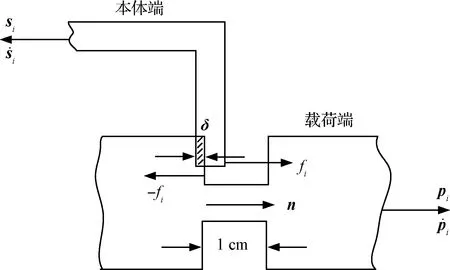
图5 音圈电机碰撞形式ⅡFig.5 Voice coil motor collision form Ⅱ

根据Hertz接触理论[19]，碰撞过程中接触力可由压痕δ的非线性函数和相对运动速度表示[20]，如式(16)所示：

(16)

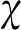
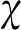
(17)

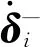
音圈电机载荷端和本体端在碰撞过程为平面接触，接触刚度系数K如式(18)所示：[22]

(18)

式中：a是接触平面等效成边长为2a的正方形的边长，σp和σs跟音圈电机载荷端和本体端接触平面的杨氏模量和泊松比有关，具体表达式如式(19)所示:

(19)

式中：E和ν分别是接触材料的杨氏模量和泊松比。

(20)

载荷模块受到的碰撞力和力矩与沿杆长方向的连续碰撞力满足式(21):

(21)

式中：f=[…,fi, …]T。

3 分离式卫星载荷模块无控碰撞仿真

当分离式卫星载荷模块处于超静超稳工作模式时，载荷模块不受到主动控制力作用。由于分离式卫星两模块在近距离相对运动，若载荷模块或服务模块受到扰动，将可能导致两模块发生碰撞。本节将仿真两模块的碰撞过程。为了让仿真结果接近实际应用工况，分离式卫星参数选择尽可能的贴近实际工况。在仿真中，根据文献[23]选择柔性线缆的刚度和阻尼，并合理考虑分离式卫星的质量特性和尺寸，分离式卫星仿真参数如表1所示

表1 分离式卫星参数Table 1 Parameters of the DPF

若音圈电机接触面材料为合金钢材，参数满足表2。

表2 音圈电机参数Table 2 Parameters of the voice coil motor

分离式卫星载荷模块受到的扰动力和扰动力矩来源于两方面：一方面源于空间环境：另一方面源于柔性线缆传递而来的服务模块扰动。

仿真中，载荷模块受到频率为0.001 Hz、幅值为10-4N的扰动力和频率为0.001 Hz、幅值为10-4N·m的扰动力矩。服务模块受到频率为0.1～1 Hz、幅值为10-3N和频率为5～10 Hz、幅值为10-2N叠加的扰动力，以及频率为0.1～1 Hz、幅值为10-3N·m和频率为5～10 Hz、幅值为10-2N·m叠加的扰动力矩。仿真过程中，载荷模块不进行主动控制，仅对服务模块进行主动控制。服务模块的姿态和位置控制律如式(22)所示：

(22)

考虑载荷模块锁紧释放过程中绕Y轴受到脉冲扰动力矩如式(23)所示:

TdY=DΔ(t)

(23)

式中：D为脉冲幅值，Δ(t)为脉冲函数。

因脉冲扰动时间较短，载荷模块绕Y轴转角不能突变，但转动角速度可突变，在脉冲扰动时间Δt内进行积分，如式(24)所示：

(24)

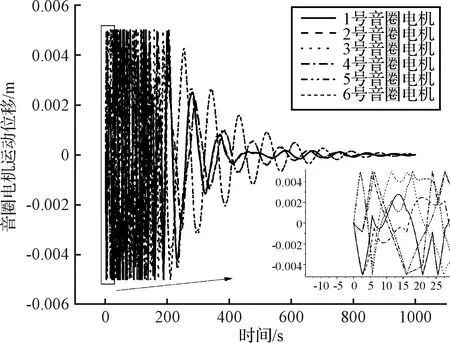
图6 音圈电机位移随时间变化Fig.6 Displacements of the voice coil motors vs. time

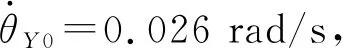
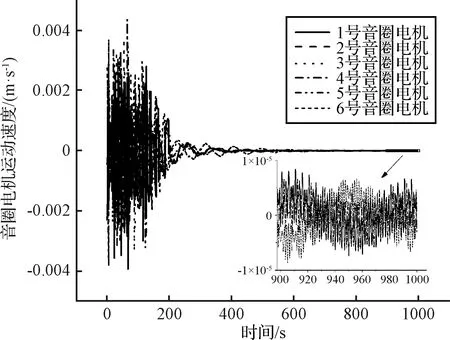
图7 音圈电机相对运动速度Fig.7 Relative velocity of voice coil motors

从图7可以看出，音圈电机相对运动速度不超过0.5 cm/s。当t=1.93 s时，6号音圈电机发生第一次碰撞，随后分离式卫星进入持续碰撞阶段，最后一次碰撞发生在t=209.14 s时刻，碰撞持续时间207.15 s。导致音圈电机发生多次碰撞的原因在于柔性线缆刚度和阻尼较小，载荷模块在运动过程中能量耗散慢，且音圈电机的运动范围仅为±0.5 cm，因此音圈电机需要多次碰撞消耗能量，才能将载荷模块的质心速度和角速度降低，使得碰撞不再发生。

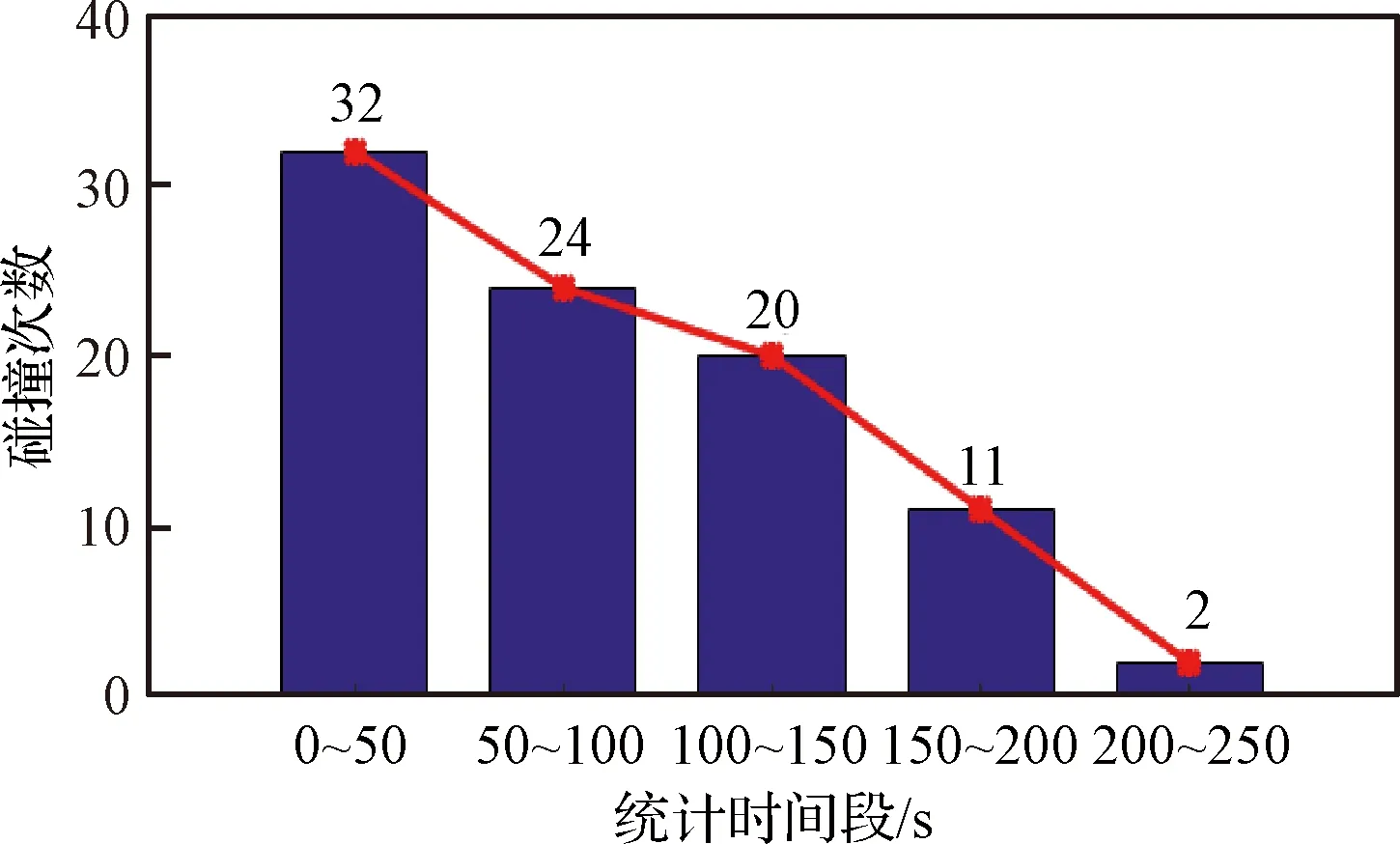
图8 音圈电机碰撞次数Fig.8 Number of collision times of the voice coil motors

以50 s为一个时间间隔，统计音圈电机在0～250 s共5个时间段内碰撞次数如图8所示。从图8可以看出，6个音圈电机共发生89次碰撞，平均每2.81 s发生一次碰撞，平均每个音圈电机发生14.8次碰撞。音圈电机在0～50 s内碰撞次数最多，共发生32次碰撞，平均每1.56 s发生一次碰撞,平均每个音圈电机发生5.3次碰撞。随着仿真时间增加，载荷模块的角速度不断降低，两次碰撞之间平均时间间隔增加。

当6号音圈电机发生第一次碰撞时，碰撞过程中产生的连续接触力如图9所示。

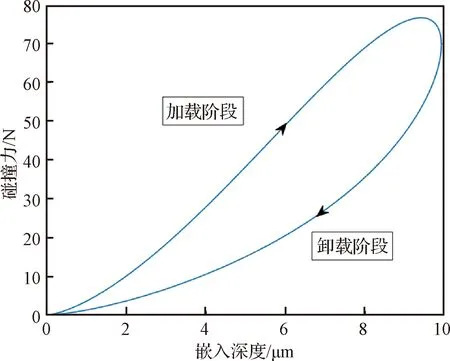
图9 第一次碰撞过程中接触力Fig.9 Contact force during the first collision

从图9可以看出，因接触力模型中存在阻尼迟滞因子，导致碰撞中加载阶段和卸载阶段接触力不沿同一路径，存在能量损失。加载阶段，当嵌入深度从0 μm增加到10 μm，接触力由0 N增加到78 N，音圈电机相对速度和碰撞前相对速度同向，接触力模型中阻尼力和弹性力同向；在卸载阶段，音圈电机相对速度和碰撞前相对速度反向，接触力模型中阻尼力和弹性力反向，导致在相同的嵌入深度下，加载阶段的接触力要大于卸载阶段的接触力。

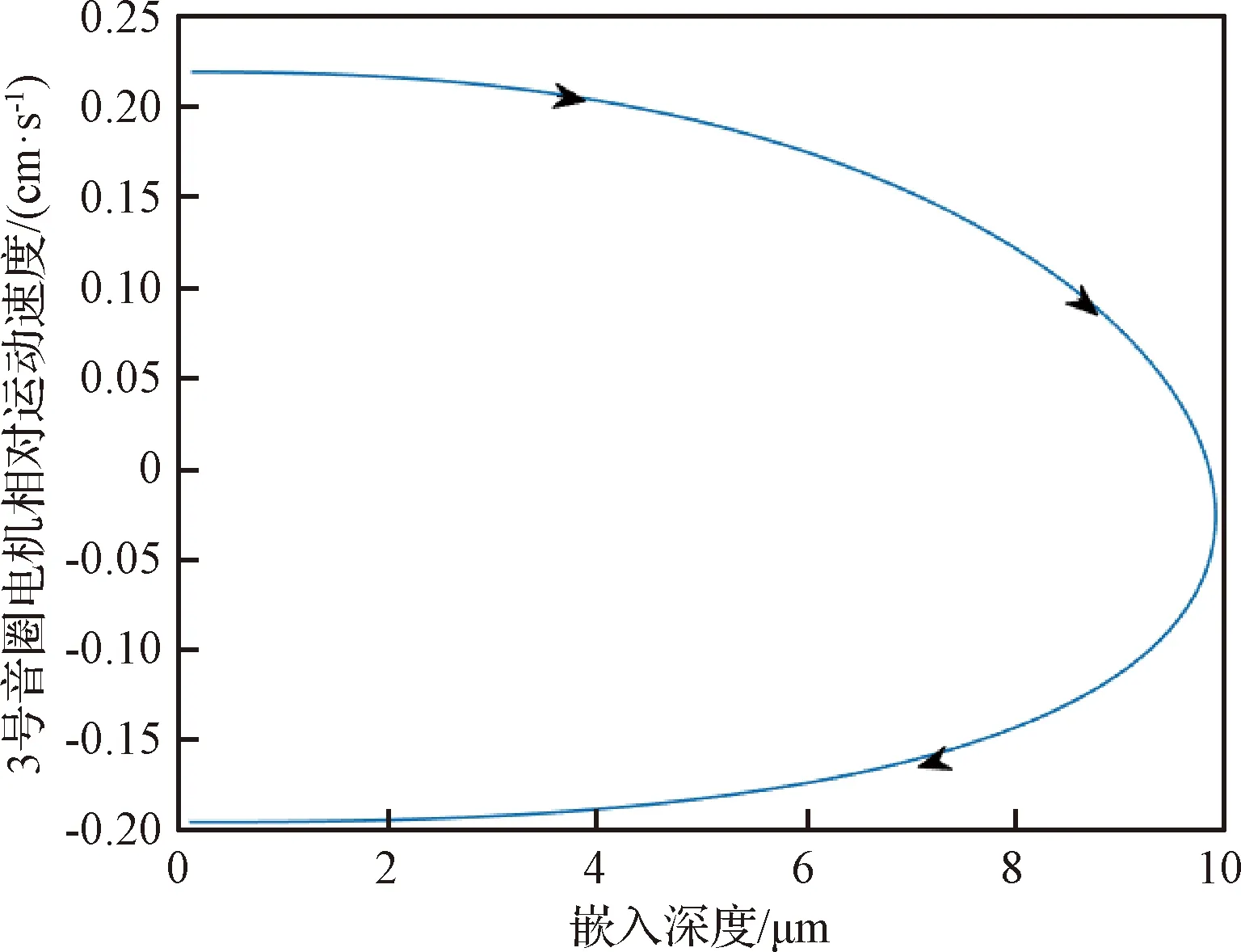
图10 第一次碰撞中6号音圈电机相对运动速度Fig.10 Relative velocity of the No.6 voice coil motor during the first collision

在发生第一次碰撞过程中，6号音圈电机相对运动速度如图10所示。从图10可以看出，当嵌入深度由0 μm增加到10 μm时，6号音圈电机相对运动速度由0.21 cm/s降低到0 cm/s。因存在能量损失，碰撞结束后相对运动速度变成-0.19 cm/s，碰撞后的动能要小于碰撞前的动能。

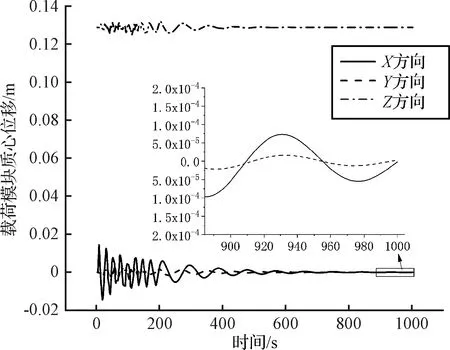
图11 分离式卫星载荷模块质心位移响应Fig.11 Response of the centroid displacement of the PM

载荷模块质心位移响应如图11所示。从图11可以看出，载荷模块质心位移在碰撞阶段，Z方向质心位移响应幅值为13.41 cm，X方向质心位移响应幅值为1.3 cm，Y方向质心位移响应幅值为0.2 cm。在完成最后一次碰撞后，载荷模块质心位移向平衡位置收敛，在1000 s时X方向和Y方向质心运动幅值小于1×10-2cm。

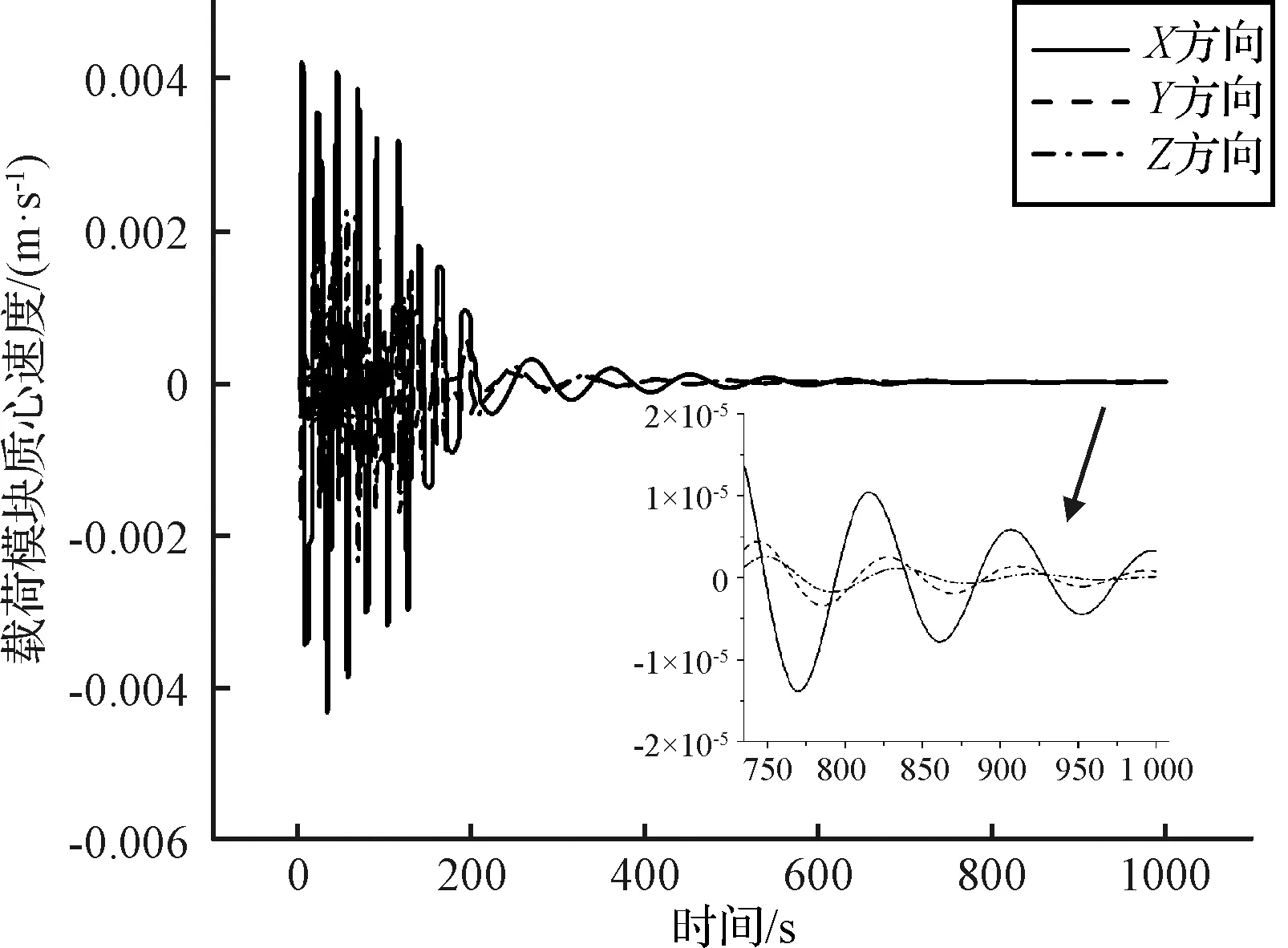
图12 载荷模块质心速度响应Fig.12 Response of the centroid velocity of the PM

载荷模块质心速度响应如图12所示。从图12可以看出，在碰撞阶段，分离式卫星载荷模块X方向质心速度响应幅值最大，达到0.45 cm/s，Z方向质心速度响应幅值达到0.26 cm/s，Y方向质心速度响应达到0.24 cm/s。从局部放大图可以看出，载荷模块质心速度在碰撞结束后会逐渐收敛至稳态值，Y和Z方向速度在1000 s时振动幅值小于1×10-3cm/s。

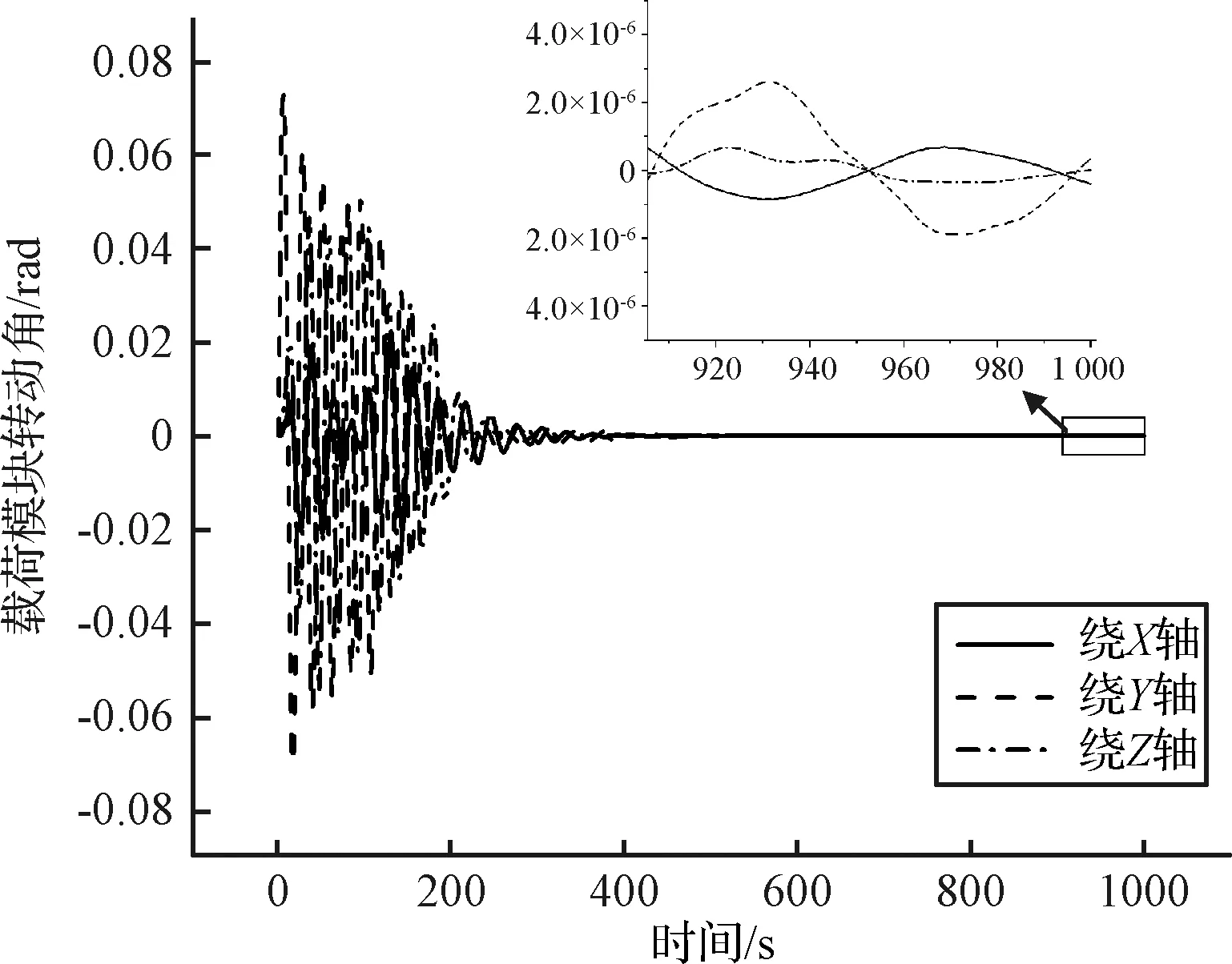
图13 载荷模块转动角响应Fig.13 Angle response of the PM

载荷模块转动角响应如图13所示。从图13可以看出，载荷模块绕Y轴最大转动角为0.071 rad。在发生第一次碰撞后，音圈电机碰撞力导致载荷模块绕X轴和绕Z轴转动角也会发生变化，绕X轴最大转动角为0.02 rad，绕Z轴最大转动角为0.051 rad。碰撞结束后载荷模块转动角逐渐收敛到稳态值，在1000 s时指向精度优于5×10-6rad，碰撞使得载荷模块指向性能下降5个数量级。

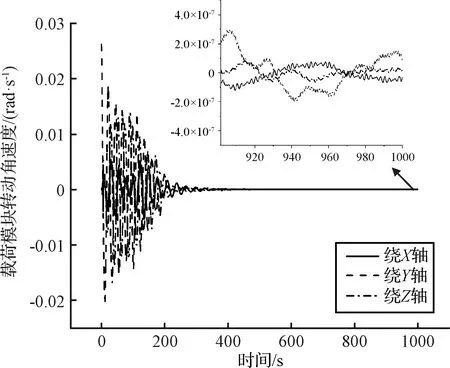
图14 载荷模块转动角速度响应Fig.14 Angular velocity response of the PM

载荷转动角速度响应如图14所示。从图14可以看出，当两模块发生碰撞时，碰撞力使得载荷模块绕Z轴转动角速度响应峰值达到-0.015 rad/s，绕X轴转动角速度达到-0.005 rad/s。载荷模块转动角速度在碰撞结束后将会收敛于稳态值，在1000 s时载荷模块的指向稳定度优于5×10-7rad/s，碰撞使得载荷模块指向稳定度下降5个数量级。载荷模块绕Y轴的转动角速度振荡收敛，随着碰撞过程中不断消耗能量，载荷模块的角速度不断降低。

以两模块发生最后一次碰撞时刻为起点，以载荷模块质心位移恢复到1×10-4m，质心速度恢复到1×10-5m/s；载荷模块转动角恢复到1×10-6rad，转动角速度恢复到1×10-8rad/s为终点，视为载荷模块恢复到超静超稳工作状态所需时间，载荷模块六自由度恢复时间统计如表3所示。

表3 载荷模块恢复超静超稳工作状态所需时间Table 3 Time required for the PM to restore the ultra-static and ultra-stable

从表3可以看出,当载荷模块受到扰动导致碰撞后,载荷模块恢复到超静超稳工作状态所需的时间长达1455 s。

4 结 论

分离式卫星载荷模块或服务模块受到扰动后可能导致两模块发生碰撞。本文基于Hertz接触理论建立了分离式卫星碰撞过程中的连续接触力模型，并仿真分析了接触力对载荷模块指向精度和指向稳定度的影响。仿真结果表明，碰撞破坏了载荷模块超静超稳工作状态，使得载荷模块指向精度和指向稳定度下降5个数量级。碰撞后载荷模块可再次恢复到超静超稳工作状态，恢复时间超过1400 s。本文对下一步研究分离式卫星受扰时碰撞规避和碰撞控制有参考价值。