无信号间干扰的相关延迟差分混沌移位键控混沌通信方案

贺利芳 陈俊 张天骐

摘 要：现有的差分混沌移位键控（DCSK）通信系统主要的缺陷是传输速率较低，为此提出了一种无信号间干扰的相关延迟差分混沌移位键控（CD-DCSK）通信方案。在发送端，由正交信号发生器产生两路正交混沌信号，并经符号函数归一化以保持发送信号的能量恒定，然后，这两路混沌信号与其延迟不同时间间隔后的混沌信号分别调制1bit数据信息形成一帧发送信号。在解调端，采用相关解调提取数据信息，通过检测相关器输出结果的符号恢复信息比特。利用高斯近似（GA）法分析了系统在加性高斯白噪声（AWGN）信道下的理论误码率（BER）性能，并与经典的混沌通信系统进行了比较。分析及实验结果表明：与DCSK系统相比，无信号间干扰的CD-DCSK系统的传输速率提升了50个百分点，且其误码性能优于相关延迟移位键控（CDSK）系统。

关键词：混沌通信;差分混沌移位键控;传输速率;误码率;相关延迟移位键控

Abstract： The major drawback of existing Differential Chaos Shift Keying （DCSK） communication system is low transmission rate. To solve the problem， a Correlation Delay-Differential Chaos Shift Keying （CD-DCSK） communication scheme without inter-signal interference was proposed. At the transmitting side， two orthogonal chaotic signals were generated by an orthogonal signal generator and normalized by the sign function to keep the energy of the transmitted signal constant. Then， two chaotic signals and their chaotic signals with different delay time intervals were respectively modulated by 1bit data information to form a frame of transmission signal. At the demodulation side， correlation demodulation was used to extract data information and the information bits were recovered by detecting the sign of correlator output. The theoretical Bit Error Rate （BER） performance of system under Additive White Gaussian Noise （AWGN） channel was analyzed by using Gaussian Approximation （GA） method， and was compared with classical chaotic communication systems. The performance analysis and experimental results indicate that， compared with DCSK system， the transmission rate of CD-DCSK system without inter-signal interference increases by 50 percentage points， and the BER performance of the proposed system is better than that of Correlation Delay Shift Keying （CDSK） system.

Key words： chaotic communication; Differential Chaos Shift Keying （DCSK）; transmission rate; Bit Error Rate （BER）; Correlation Delay Shift Keying （CDSK）

0 引言

混沌信號具有一些优良的特性，例如长期不可预测性、初值的极端敏感性、非周期性、类随机性及产生设备简单等，使其非常适合于保密通信、扩频通信等领域[1-4]的应用。诸多专家学者已对这一领域进行了深入而细致的研究。在过去几十年中，研究人员已经提出了许多基于混沌的非相干通信方案[5-1011]。

在混沌数字通信领域，文献[12]文献未按顺序依次引用，漏引了文献11，是否可以加在前面的引用，即5-10，改为5-11？请明确。

回复：

1. 针对参考文献[11]未引用的问题，提出两种修改意见：

1） 修改论文中的参考文献标注序号，将参考文献序号[12]改为[11]，相应的文中此序号之后的所有参考文献标注序号依次减一。

2） 在引言段将参考文献标注[5-10]改为[5-11]，并在论文最后的参考文献[10]之后，插入参考文献[11]，如下：

[11] 代红英， 徐位凯. MC-DCSK中的子载波功率分配优化算法[J]. 重庆邮电大学学报（ 自然科学版）， 2015， 27（2）： 170-173. （DAI H Y， XU W K. Optimal sub-carriers power allocation in MC-DCSK communication system （Natural Science Edition） [J]. Journal of Chongqing University of Posts and Telecommunications， 27（2）， 170-173.）

采用第二种方法

提出的差分混沌移位键控（Differential Chaos Shift Keying， DCSK）和文献[13]中提出的相关延迟移位键控（Correlation Delay Shift Keying， CDSK）调制技术是最为经典的。DCSK方案采用了传输参考技术，在发送端利用开关将参考信号和数据信息分开传输。该方案拥有良好的误码性能，但是信息传输速率不高，保密性差，不能连续发送信号。为了解决上述问题，文献[13]中提出了CDSK方案，将DCSK系统中发送端的开关替换成加法器，有效提升了信息速率。该方案在提高信息传输速率的同时也引入了过多的信号内干扰，因此，系统的误码性能较差。近年来国内学者对DCSK技术的研究也取得了许多成果，例如，文献[14]中提出了一种高速差分混沌键控（High Rate Differential Chaos Shift Keying， HR-DCSK），通过缩短参考信号的长度，同时传输2bit信息来提高传输速率。文献[15]中提出的无码间干扰的差分混沌相关延迟移位键控（Differential Chaos-Correlation Delay Shift Keying， DC-CDSK），通过改变发送信号的帧结构，将一帧分为3个相等时隙来传输2bit信息以达到提高传输速率的目的，但是其数据传输速率仍然较低。

为了提高DCSK系统的传输速率而又不过多地增加系统设计的复杂性，结合CDSK系统的特点，在无码间干扰的DC-CDSK系统的基础上，本文提出了一种无信号间干扰的相关延迟差分混沌移位键控（Correlation Delay-Differential Chaos Shift Keying， CD-DCSK）混沌通信方案。引入一种简单的正交混沌信号发生器使得生成的两路混沌序列彼此正交，从而消除判决变量中两路混沌信号之间的干扰;同时引入符号函数，使系统的比特能量恒定。利用高斯近似（Gaussian Approximation， GA）法对系统的理论误码性能进行了分析，给出了误码率公式，并将其与典型的系统进行了比较。与DCSK系统相比，本文系统的传输速率提升了50个百分点，并且本文系统的设计没有过多地增加复杂的硬件设备，很容易实现，因此，本文系统更适用于实际的混沌通信系统。

1 经典的混沌通信系统

DCSK系统和CDSK系统是混沌数字通信领域中两种最为典型的系统。近年来提出的一些方案，许多也是基于这两种系统进行的改进，下面将简单介绍一下这两种系统。

1.1 DCSK系统

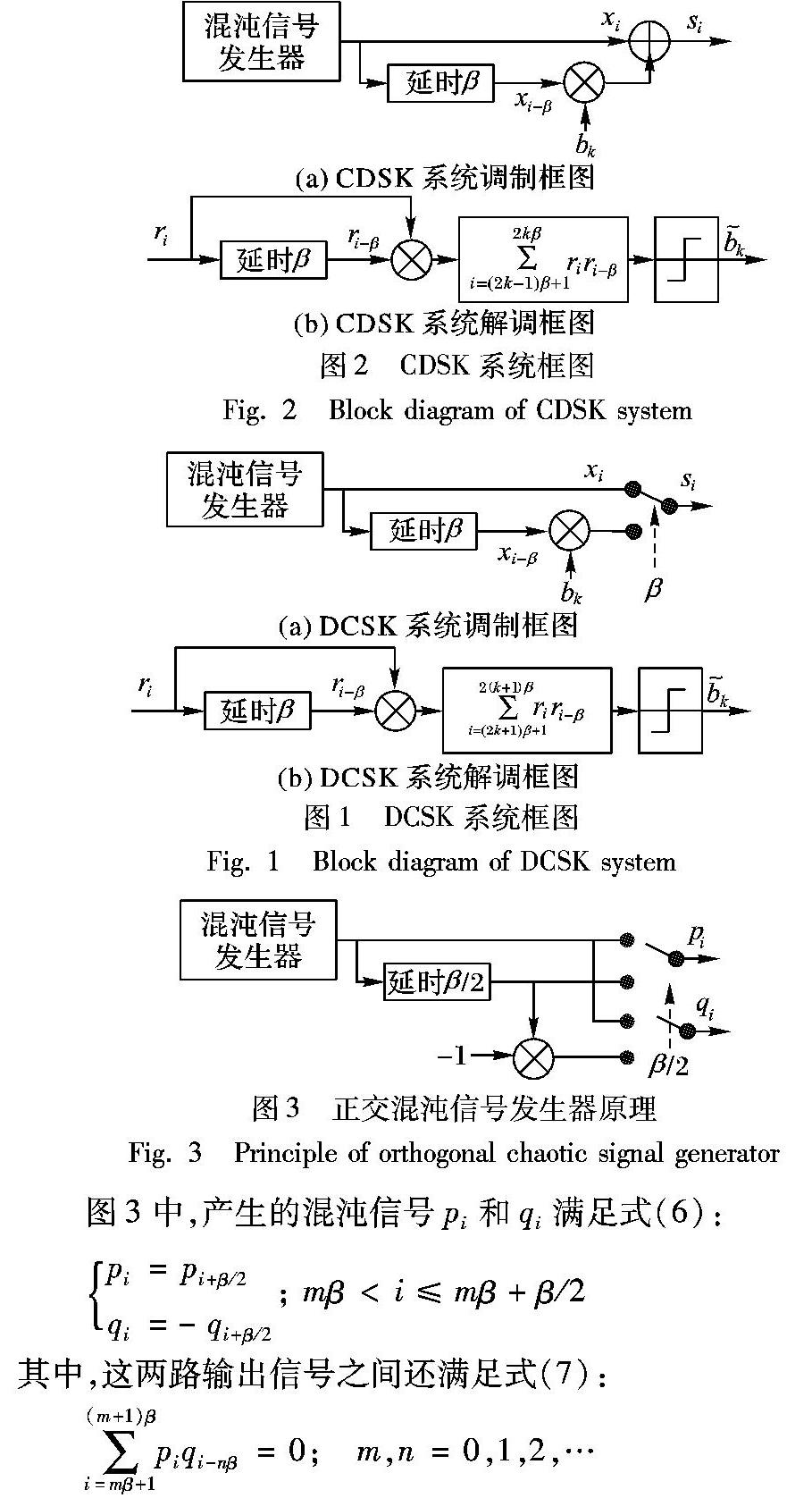
图1（a）为DCSK系统调制框图。此方案中，一个信息帧被均等地分为两个时隙。前一时隙发送的信号作为参考，后一时隙则发送信息信号。

其中：bk∈{+1，-1}表示第k个信息比特， β表示一个时隙内传输信号的采样数。若信息比特bk是+1，则信息信号与参考信号完全一样;反之，若bk为-1，则信息信号等于负的参考信号。根据扩频因子（Spreading Factor， SF）的定义，DCSK系统满足SF=2β。

图1（b）为DCSK系统的解调框图。接收机使用一个相关器将信号ri与延迟β时间后的信号ri-β做相关，得到bk的判决变量Zk。将Zk送入相应的判决器，根据判决器输出值的正负，可恢复出bk。由以上分析，易得接收端相关器输出为：

DCSK系统的信号发送端采用开关结构发送数据信息，仅有混沌信号与噪声以及噪声与噪声间的干扰，不存在码间干扰，因而具有良好的误码性能。根据以下判决准则来进行信息比特的解调：

1.2 CDSK系统

图2（a）为CDSK系统调制框图。与DCSK系统不同，在CDSK方案中，发送的信号是混沌序列xi与其自身延时采样数β并经过二进制符号调制的信号之和。

图片

CDSK系统也采用相关解调来恢复信息比特。其解调的判决准则同DCSK系统，此处就不再赘述。在发送端CDSK系统利用加法器将参考信号和信息比特同时传输，提高了信息的传输速率，但是也引入了混沌信号的交叉干扰以及更多的信号与噪声间的干扰，因此其误码性能较差。根据图2（b），易知CDSK系统相关器的输出为：

2 无信号间干扰的CD-DCSK系统原理

本系统在信号发送端采用两路正交信号调制2bit数据信息，以提高系统传输速率。虽然系统的传输速率提高了，但是其误码性能较差，为此本文借鉴一种简单的正交混沌信号发生器[16]，生成两路正交的混沌序列，消除两路混沌信号间的相关干扰，以改善其误码性能。其原理如图3所示。

其正交原理如下：在前β/2（β表示一个时隙内传输信号的采样数）时间内，序列pi和qi相同;在后β/2时间内，pi等于负的qi。这就使得一个β采样时间内序列pi和qi严格正交。

图4（a）为无信号间干扰的CD-DCSK系统的调制框图。下面以第k帧传输信号为例，简述其调制原理。图4（a）中正交混沌信号发生器产生的两路混沌序列，先经过符号函数映射成序列xi和yi，然后xi经过信息比特b2k调制后的数据信号与yi之和在前半帧发送;而xi延时β后的信号xi-β与yi延时3β后经过信息比特b2k+1调制的信息信号之和在后半帧发送。

图4（b）是其解调框图。接收机使用两个独立的相关器分别运算信息比特b2k和b2k+1的相关值，得判决变量Z2k和Z2k+1，然后將Z2k和Z2k+1分别送入门限判决器，最终根据判决器输出值的正负号可恢复出b2k和b2k+1。

假设信号在传输过程中仅受加性高斯白噪声干扰，则接收信号ri可表示为：

其中：si为发射信号;ni是零均值，方差为N0/2的加性高斯白噪声。

接收端信息比特b2k的相关输出为：

3 系统性能分析

为了验证所提出方案的优越性，需要从理论和实验两方面来分析系统的误码性能。本章将利用高斯近似法从理论上分析所提出方案的误码性能。改进型Logistic映射易于实现，因此，本文选用该映射产生混沌序列pi，再经过符号函数映射成二进制序列xi，如式（16）：

根据文献[17]此处确实指文献17吗？因为原来的文献是总共16条，增加了新的文献11？请明确，经符号函数映射后的混沌序列xi和yi，有如下统计特性：

4 仿真分析

本章将在AWGN信道中，利用蒙特卡罗（Monte Carlo）方法对无信号间干扰的CD-DCSK系统进行仿真分析。仿真中的混沌序列均由Logistic映射产生，仿真图中的数值均是在105次模拟实验取平均值条件下得到的。

4.1 实验值和理论值的比较

图5是采样数β（β分别为20、50、100）的不同取值时，无信号间干扰的CD-DCSK系统的误码率的理论值和其相应的实验值随信噪比Eb/N0变化的曲线。由图5可看出当混沌序列长度β较大时（β=50、100），误码率的理论值和实验值相一致，证明理论公式推导的正确性;当β较小时（β=20），误码率的理论仿真曲线和实验仿真曲线有较大偏差。这是由于β较小时，系统的有用信号项实际上并不服从高斯分布，所以会出现理论仿真曲线与Monte Carlo仿真曲线不吻合的情况，这是高斯近似法的局限性所导致的。由式（21）给出的系统理论误码率公式分析可知，当Eb/N0一定时，系统的误码率随着β值的增大先减小后增大，不同的β值，可能会有相同的误码率;只有当β取得式（22）的最佳值时，系统取得式（23）给出的最小误码率，因此，图5中不同β取值时曲线会有交点。这与理论分析是吻合的。

4.2 混沌序列长度对系统的影响

图6是不同信噪比（Eb/N0）取值时，无信号间干扰的CD-DCSK系统误码率随采样数β变化的曲线。此处Eb/N0的取值分别为10dB、12dB、15dB及18dB。由图6可知，系统误码性能受β值影响较大。对于某个特定的Eb/N0，系统误码率随着β值的增大先减小后增大，因此，存在最佳β值（βopt）使系统误码率最小。这与图5的仿真曲线是不矛盾的。当β<βopt时，混沌序列的自（互）相关性随着β的增大不断增强，最终使其相关值趋于稳定，系统中的干扰逐渐减小，误码率降低;当β>βopt时，随着β的继续增大，噪声干扰的方差增大，此时噪声干扰是影响系统误码性能的最主要因素，所以系统误码率又逐渐增大;当β=βopt时，混沌信号相关值的减少量与噪声干扰项方差的增加量相等，致使这两部分干扰相互抵消，此时系统拥有最佳的误码性能。

4.3 不同系统之间的比较

图7绘出了β=20和β=50，无信号间干扰的CD-DCSK系统、DCSK系统及CDSK系统的误码性能随Eb/N0变化的曲线。由仿真曲线可见，任意Eb/N0条件下，无信号间干扰的CD-DCSK系统的误码性能均优于CDSK系统，但是仍次于DCSK系统。虽然本文系统的误码性能仍不如DCSK系统，但是其传输速率与DCSK系统的传输速率相比，提高了50个百分点，所以本文系统仍具有一定优势。

图8所示为β=100时，无信号间干扰的CD-DCSK系统与无码间干扰的DC-CDSK系统[15]的性能对比曲线。表1列出了几种经典系统的数据传输速率。通过图8的对比可以发现，在相同混沌序列长度（β）条件下，对于较大的信噪比，本文方案误码性能并没有无码间干扰的DC-CDSK系统好，但是本文方案的数据传输速率要高于无码间干扰的DC-CDSK系统，这一点由表1可看出。

5 结语

本文针对DCSK系统信息速率低的缺陷，结合DCSK系统及CDSK系统发射机的结构特点，设计并研究了一种无信号间干扰的CD-DCSK混沌通信系统。借鉴CDSK系统发射端利用加法器的思想，把两路DCSK系统合并在一起，同时引入了正交混沌信号发生器，并使用二进制混沌序列作为载波，在提高数据传输速率的同时，减轻了噪声干扰。该系统结构简单、易实现，较好地解决了DCSK系统传输速率低的问题，因此，该方案更适用于实际混沌通信系统;但是该系统的误码性能并没有DCSK系统好，这也是该方案的一个最大缺陷。下一步的研究重点是在保证系统现有传输速率不变的情况下，进一步提高系统的误码性能。

参考文献 （References）

[1] SANGEETHA M， BHASKAR V. NR-DCSK based chaotic communications in MIMO multipath channels [J]. Wireless Personal Communications， 2018， 103（2）： 1819-1834.

[2] 趙雅琴，李书营，米雪龙，等.基于STBC技术的DCSK通信系统性能分析[J].系统工程与电子技术，2016，38（1）：155-162.（ZHAO Y Q， LI S Y， MI X L， et al. Performance analyze for STBC-based DCSK communication system [J]. Systems Engineering and Electronics， 2016， 38（1）： 155-162.）

[3] ESCRIBANO F J， KADDOUM G， WAGEMAKERS A， et al. Design of a new differential chaos-shift-keying system for continuous mobility [J]. IEEE Transactions on Communications， 2016， 64（5）： 2066-2078.

[4] KADDOUM G， TRAN H V， KONG L， et al. Design of simultaneous wireless information and power transfer scheme for short reference DCSK communication systems [J]. IEEE Transactions on Communications， 2017， 65（1）： 431-443.

[5] GALIAS Z， MAGGIO G M. Quadrature chaos-shift keying： theory and performance analysis [J]. IEEE Transactions on Circuits and Systems I： Fundamental Theory and Applications， 2001， 48（12）： 1510-1519.

[6] KADDOUM G， RICHARDSON F， GAGNON F. Design and analysis of a multi-carrier differential chaos shift keying communication system [J]. IEEE Transactions on Communications， 2013， 61（8）： 3281-3291.

[7] LAU F C M， CHEONG K Y， TSE C K. Permutation-based DCSK and multiple-access DCSK systems [J]. IEEE Transactions on Circuits and Systems I： Fundamental Theory and Applications， 2003， 50（6）： 733-742.

[8] YANG H， JIANG G P. High-efficiency differential-chaos-shift-keying scheme for chaos-based noncoherent communication [J]. IEEE Transactions on Circuits and Systems II： Express Briefs， 2012， 59（5）： 312-316.

[9] XU W K， WANG L， KOLUMBAN G. A novel differential chaos shift keying modulation scheme [J]. International Journal of Bifurcation and Chaos， 2011， 21（3）：799-814.

[10] KADDOUM G， GAGNON F. Design of a high-data-rate differential chaos shift keying system [J]. IEEE Transactions on Circuits and Systems II： Express Briefs， 2012， 59（7）： 448-452.

[11] 代紅英，徐位凯.MC-DCSK中的子载波功率分配优化算法[J].重庆邮电大学学报（自然科学版），2015，27（2）：170-173.（DAI H Y， XU W K. Optimal sub-carriers power allocation in MC-DCSK communication system [J]. Journal of Chongqing University of Posts and Telecommunications （Natural Science Edition）， 2015， 27（2）： 170-173.）

在论文最后的参考文献[10]之后，插入参考文献[11]，如下：

[11] 代红英， 徐位凯. MC-DCSK中的子载波功率分配优化算法[J]. 重庆邮电大学学报（ 自然科学版）， 2015， 27（2）： 170-173. （DAI H Y， XU W K. Optimal sub-carriers power allocation in MC-DCSK communication system （Natural Science Edition） [J]. Journal of Chongqing University of Posts and Telecommunications， 27（2）， 170-173.）

[12] KOLUMBAN G， KENNEDY M P， CHUA L O. The role of synchronization in digital communications using chaos-part II： chaotic modulation and chaotic synchronization [J]. IEEE Transactions on Circuits and Systems I： Fundamental Theory and Applications， 1998， 45（11）： 1129-1140.

[13] SUSHCHIK M， TSIMRING L S， VOLKOVSKII A R. Performance analysis of correlation-based communication schemes utilizing chaos [J]. IEEE Transactions on Circuits and Systems I： Fundamental Theory and Applications， 2000， 47（12）： 1684-1691.

[14] 张刚，郝怡曼，贺利娜.一种高速差分混沌移位键控系统[J].电讯技术，2017，57（6）：672-677.（ZHANG G， HAO Y M， HE L N. A high rate differential chaos shift keying system[J]. Telecommunication Engineering， 2017， 57（6）： 672-677.）

[15] 张刚，许嘉平，张天骐.无码间干扰DC-CDSK混沌通信方案[J].电讯技术，2018，58（4）：418-423.（ZHANG G， XU J P， ZHANG T Q. A DC-CDSK chaotic communication system without inter-symbol interference [J]. Telecommunication Engineering， 2018， 58（4）： 418-423.）

[16] 杨华，蒋国平，段俊毅.无信号内干扰的高效差分混沌键控通信方案[J].通信学报，2015，36（6）：150-155.（YANG H， JIANG G P， DUAN J Y. High efficiency differential chaos shift keying modulation scheme without intra-signal interference[J]. Journal on Communications， 2015， 36（6）： 150-155.）

[17] MANDAL S， BANERJEE S. Analysis and CMOS implementation of a chaos-based communication system [J]. IEEE Transactions on Circuits and Systems I： Regular Papers， 2004， 51（9）： 1708-1722.