蜂群双抑制劳动分工算法及其在交通信号配时中的应用

胡亮 肖人彬 李浩

摘 要：群智能劳动分工是指任何启发于群居性昆虫和其他动物群体的集体行为而设计的算法和分布式问题解决方式，可以广泛用于现实生活中的任务分配问题。针对交通信号配时这类任务分配问题，引入描述蜜蜂个体之间交互方式的劳动分工理论，提出了一种基于群智能的蜂群双抑制劳动分工算法（BDILDA），该算法通过个体内部抑制剂和外部抑制剂的相互作用，达到群体劳动分工的动态调节。为了验证BDILDA的有效性，选取交通信号配时问题进行仿真实验。采用BDILDA对实际案例进行了交通信号配时求解，并把所得结果与Webster算法、群智能多种群蚁群算法（MCAA）、迁移蜂群（TBO）算法和反向烟花算法（BFWA）得出的结果进行了对比。实验结果显示所提算法减小平均延误时间14.3～20.1个百分点，减少平均停车次数3.7～4.5个百分点，在最大通行能力方面增加5.2～23.6个百分点。结果表明该算法适于求解不确定环境下的动态分配问题。

关键词：群智能;劳动分工;蜂群双抑制原理;交通信号配时

Abstract： Swarm intelligence labor division refers to any algorithm and distributed problem solving method that is inspired by the collective behaviors of social insects and other animal groups. It can be widely used in real-life task assignment. Focusing on the task assignment problem like traffic signal timing， the theory of labor division that describes the interaction mode between bee individuals was introduced， a Bee colony Double Inhibition Labor Division Algorithm （BDILDA） based on swarm intelligence was proposed， in which the dynamic accommodation of swarm labor division was achieved through interaction between internal and external inhibitors of the individual. In order to verify the validity of BDILDA， the traffic signal timing problem was selected for simulation experiments. BDILDA was used to solve actual case of traffic signal timing and the result was compared with the results of Webster algorithm， Multi-Colony Ant Algorithm （MCAA）， Transfer Bees Optimizer （TBO） algorithm and Backward FireWorks Algorithm （BFWA）. The experimental results show that average delay time of BDILDA is reduced by 14.3-20.1 percentage points， the average parking times is reduced by 3.7-4.5 percentage points， the maximum traffic capacity is increased by 5.2-23.6 percentage points. The results indicate that the proposed algorithm is suitable for solving dynamic assignment problems in uncertain environment.

Key words： swarm intelligence; labor division; bee colony double inhibition principle; traffic signal timing

0 引言

隨着社会科技的快速发展，人们对高效智能的生活提出了更高更新的要求。然而，由于现实生活中大多数问题具有复杂性、动态性、非线性和建模困难等特点，现有的智能算法已经很难满足实际的需求。比如常见的交通信号配时问题，城市的汽车数量呈现指数级增长，随之而来的就是严重的交通拥堵和环境污染问题。交通信号实时控制系统是减少城市交通网的交通延误，利用道路设施，减小交通事故、环境污染以及汽油消耗等有效手段，是城市交通管理的有力工具[1]。现有的城市红绿灯控制系统虽然在一定程度上可以满足指挥路口交通的需要，但随着城市车辆的增加，城市拥堵情况越来越严重，原有的红绿灯控制系统已经显示出明显的缺点：红绿灯不同信号时间相对固定，难以根据车流量的改变而动态调整红绿灯的显示时间，因此常常会遇到这样的情况，在一个十字路口，本车道非常拥堵，而垂直车道非常空闲，但是红绿灯仍然不能优先照顾已十分拥堵的车道，只能机械地变换。寻找各种适用于领域实践需求的新兴的智能计算技术已经成为越来越多研究者的关注焦点。在没有集中控制且不提供全局模型的前提下，群智能劳动分工为寻找复杂的分布式问题的解决方案提供了基础。

群智能劳动分工[2-3]是一种普遍存在于社会性昆虫中的生物集群行为，也是当前群智能研究的一个新兴领域，它是由自然或人造的分散自组织系统所表现出来的集体智能。群智能包含一组简单的个体，其中个体与个体、个体与环境之间存在局部交互行为。虽然个体遵循非常简单的规则，但微观层面的个体交互最终还是导致了宏观的智能行为，族群中的个体不具备任何有关群体需求的信息，仅仅依靠简单的行为规则决定自身的行为，并且不断与周围个体进行交互作用，最终使族群涌现出令人惊叹的智能。对社会性昆虫而言，族群效率取决于个体在不同任务上的分配情况。经常认为劳动分工作用下个体的分工恰好符合族群对各项任务的要求，正是社会性昆虫生态成功的首要原因。

交通信号配时问题作为一种典型的复杂性问题，不仅环境动态多变而且建模困难。现有的智能优化算法很难解决这样的问题，而群智能劳动分工在解决这类问题有着不错的效果，因此，本文以交通信号配时为代表，将群智能劳动分工用于求解交通信号配时问题。本文借鉴群智能劳动分工的任务分配方式来实现交通信号配时问题的时间分配，提出一种基于群智能劳动分工理论的蜂群双抑制劳动分工算法（Bee colony Double Inhibition Labor Division Algorithm， BDILDA），该算法继承了群智能劳动分工的高效性和分配柔性，根据外部环境的变化动态自组织分配绿灯时间，能有效弥补现有交通信号配时问题求解方法存在的收敛速度慢、对交通流量动态变化适应性差的不足。

1 交通信号配时问题分析

1.1 交通信号配时问题介绍

十字交叉口是一种简单而又普遍存在的交叉口类型，本文以常见的十字交叉路口的交通信号配时为实验对象[4]。交叉口有东、西、南、北四个方向，每个方向都有左行、直行和右行三个方向的车流。交叉口交通信号配时主要涉及三部分内容：信号相位的确定、配时参数的选择以及运行效率的衡量。

导致交叉口信号配时的主要设计参数有信号周期和绿信比。信号周期指信号灯各种灯色轮流显示一周所需的时间，即各种灯色显示时间之和，或是从某相位的绿灯启亮开始到下次该绿灯再次启亮之间的一段时间。信号周期用C表示，单位为秒（s）。

由于信号在相位变换时不可避免地会造成时间的损失，在实际显示的绿灯时间内必然有一段损失时间，而真正用于车辆通行的那段时间被称为有效绿灯时间。绿信比指在一个信号周期内，某一相位的有效绿灯时长xi与信号周期时长C之比，一般用λi表示：

配时参数下交通效益的评价指标一般有延误时间、停车次数、通行能力、排队长度、尾气排放及油耗等[5]。由于前三个指标相对容易计算，在已有研究中得到了较多的采纳。本文选取延误时间、停车次数和通行能力作为衡量指标，其中延误时间和停车次数体现了道路使用者的利益，越小越好;通行能力体现了道路的使用效率，越大越好。

1.2 面向交通信号配时的群智能劳动分工

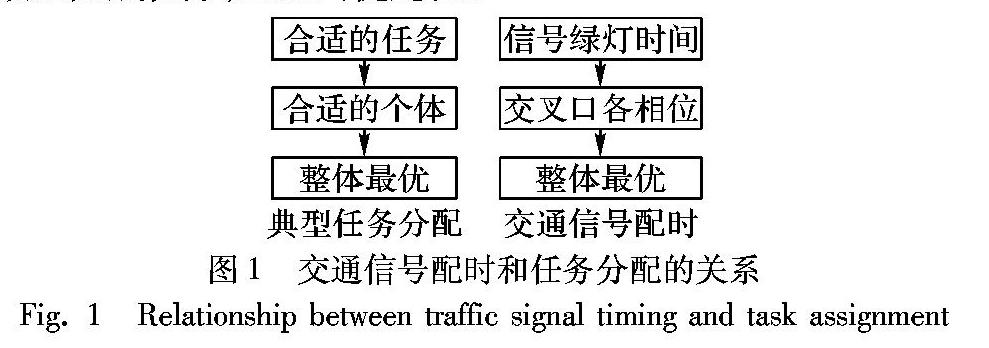
目前国内外研究交通信号灯配时优化的方法主要是蚁群算法[7]、模拟退火[8]、神经网络[9]、遗传算法[10]等智能优化算法。上述智能优化算法在求解交通信号配时问题时都有一个共同的特点，它们都是把交通配时问题看作一个优化问题，都是通过建立优化模型，求解目标函数最小值。现代交通系统具有复杂多变的不确定因素，现有的智能优化算法很难有效解决这样的问题。这种设计优化模型的求解方式在处理静态问题的时候效果不错，但是在处理动态问题的时候，往往很难根据环境的变化进行及时的动态调整[11];而交叉口的车流量是动态变化的，既有规律性的变化（如潮汐交通），也有非規律的变化（如节假日、天气变化等）。动态变化的车流量需要信号周期、各相位绿灯时间等配时参数能作出适应性的动态调整。通过分析交通信号配时的特点本文发现交通配时问题就是一个典型的动态变化的任务分配问题。任务分配问题研究的核心就是如何将合适的任务分配给合适的Agent以实现整体执行效果最优，而交通配时问题就是研究如何将合适的信号绿灯时间分配给合适的相位以实现整个交叉口的交通性能最优，如图1所示，因此可以把交通配时问题看成是任务分配问题，对于这种问题，群智能劳动分工能有效而快速地实现任务的灵活分配，具有明显的适应性，在动态环境下仍能高效地完成任务，显示出优越性。

目前，群智能劳动分工模型的应用主要集中在解决现实生活中的任务分配问题，同时劳动分工的自组织、自适应特性也使其在许多领域体现出发展优势[12-15]。通过观察和分析交通信号配时问题的特点，可以发现交通灯信号控制其实与生物群体行为有着相似之处，即可以将交通灯信号控制抽象成一个任务分配问题，每一个路口的交通灯虽然是独立的个体，但是它们的整体控制却是一个群体行为，据此可以借鉴群智能劳动分工理论来实现个体的绿灯时间分配以达到动态环境下的群体最优。

2 求解交通信号配时问题的蜂群双抑制劳动分工算法

2.1 蜂群双抑制劳动分工原理

Bonabeau等[16]认为：群智能是指众多无智能的主体组成的群体，通过相互间的合作表现出智能行为的特性。它受启发于社会性昆虫或动物的群集行为，在研究自然界的生物群体系统时，研究者惊奇地发现，昆虫群体中的单个个体所表现的行为是缺乏智能的，但是个体所组成的群体则表现出了一种有效的复杂的智能行为。群体系统仅仅是依靠一套在个体间和个体与环境间简单的交互规则，就可以具有鲁棒性和高超的解决问题能力，例如，蚂蚁发现新的食物源、黄蜂在群体内部进行劳动分工，构筑复杂的巢穴、鸟类跨越几千公里迁徙到指定地区等。个体可以很快地适应群体组织的变化和应对外界的挑战，这些能力在工程优化和计算机科学中有着非常重要的价值。群体智能系统由相对简单的个体组成，与昆虫社会类似，个体遵循简单的行为规则，只有局部感知和通信功能，因此，个体之间的交互以及个体与环境之间的交互仅限于局部范围。由于群系统的动态属性，这些交互具有一定的随机性。尽管没有集中控制，但是这类系统表现出超出个体能力的全局涌现行为。

本文主要从蜂群入手，研究蜂群劳动分工。蜂群的群智能劳动分工主要表现在时间多态上。在时间多态中，蜜蜂的年龄与其执行的任务之间通常存在相关性。蜜蜂之间以日龄为基础的分工达到高水平的群体统一，一般蜜蜂的成年生活开始的前3周在蜂巢里工作，最后的1～3周进行采集活动，但为了适应群体或环境条件的改变，蜜蜂能加快、阻碍、颠倒它们行为的发展[17]。蜜蜂年龄发生的行为变化与生理变化有关。这些变化包括内分泌腺的激活和退化，信息素产生的变化以及与任务表现相关的刺激反应的变化。幼年激素（Juvenile Hormone， JH）在行为发育调控中起着重要作用;JH的滴度通常与行为状态相关，并且涉及JH的添加或去除分别引起行为发展的加速或迟缓的处理[18]。JH被描述为起搏器，因为它影响发育变化的速率和时间。

Amdam等[19]学者在针对蜂群活动的研究过程中，为了解释蜜蜂从巢内蜂向觅食蜂分化的现象，提出了双抑制假说（double inhibition hypothesis）。该假说（图2）提出蜜蜂体内有两种抑制剂——内部抑制剂（Internal Repressor， IR）和外部抑制剂（External Repressor， ER），两者共同对神经系统（Allatoregulatory Central Nervous System， ACNS）产生抑制作用。ACNS的作用是能够促进JH的生成，进而产生依赖于保幼激素的分化途径（Juvenile Hormone-Dependent Differentiation pathway， JHDD），并且ACNS能够直接促进一种不依赖于JH的分化途径（Juvenile Hormone-Independent Differentiation pathway， JHID）的产生。JH对卵黄蛋白原的合成有抑制作用，卵黄蛋白原的含量与内部抑制剂的含量是正相关的，而外部抑制剂的产生则来自于蜜蜂个体之外的其他蜜蜂，准确地说，是源自于当前个体所接触到的觅食蜂，接触的觅食蜂越多，则ER越多。

下面说明ER与IR的作用机制：

1）当缺少足够的ER时（即觅食蜂数量不足时），ACNS受到的抑制降低，一方面激发JHID的分化途径产生，另外一方面通过促使JH含量的增加激发JHDD分化途径，所以蜜蜂从巢蜂到觅食蜂的分化提前，觅食蜂数量增加。另外JH增加导致IR减少，形成了一个正反馈通路，进而巩固已经得到的分化成果，使新的觅食蜂保持在觅食状态。

2）当缺乏碳水化合物以及蛋白质时，卵黄蛋白原的消耗会加速，IR含量会下降，正反馈回路再次形成，同样会导致巢蜂的分化，觅食蜂数量增加。

蜂群双抑制原理以个体个体交互的方式完成任务分配，参考Naug等[20]进一步描述了蜂群双抑制原理中个体间的交互方式，建立个体间交互关系如图3所示。蜂群中每只蜜蜂都包含一个激发剂J和两个抑制剂IR和ER。J是蜜蜂内在的激发剂，对蜜蜂自身的行为发育起促进作用。IR是蜜蜂内在的抑制剂，不会阻碍自身的行为发育，但在个体交互过程中会对其他蜜蜂的行为发育产生抑制作用。ER是蜜蜂在交互作用中得到的外在抑制剂，会阻碍自身的行为发育。最终，激发剂J和抑制剂的相对水平（J/（αIR+ER））决定蜜蜂的行为发育是按照正常速度还是被加速、延迟或逆转。

2.2 双抑制劳动分工映射模型提出

蜂群的这种具有自我调节机制的劳动分工方式，为解决类似任务分配问题提供了新的思路。参考Amdam等学者的双抑制假说，本文建立基于蜂群劳动分工现象的双抑制交通配时映射模型。该模型以蜜蜂个体为建模对象，试图通过蜜蜂个体的简单行为的叠加以实现蜂群整体的合理劳动分工。

该算法的核心思想是：1）将交通信号灯的每一个信号相位看作一只蜜蜂;2）将信号相位的绿灯时间看作蜜蜂的生理年龄;3）将信号相位的停车次数看作蜜蜂的外部抑制剂;4）将信号相位的通行能力看作蜜蜂的内部抑制剂;5）将信号相位的延误时间看作蜜蜂的激发剂。某一信号相位的延误时间越长，则其激发剂越大，在双抑制原理作用下，其绿灯时间将会增加;延误时间越长，相应的停车次数也越大，则外部抑制剂越大，在双抑制原理作用下，其他相位的绿灯时间将会减小。通过激发剂和抑制剂的变化自适应调整各信号相位的绿灯时间完成时间分配，具有原理简明、易于实现的特点。

下面建立公式中的变量与实际问题参量之间的映射关系，如图4所示。

这样采用群智能劳动分工的求解方式，随着时间的变化，交通路口各个相位的时间就可以根据各相位的车流量实现动态调节，并且在不需要建立优化模型的前提下就可以达到自适应地减小车辆的平均延误时间的目的。

2.3 蜂群双抑制劳动分工算法

基于图4描述的映射关系，本节提出一种面向交通信号配时问题的蜂群双抑制劳动分工算法（BDILDA）。BDILDA的核心要点是：某一信号相位的延误时间越长，则其激发剂越大，在激发抑制原理作用下，其绿灯时间将会增加;延误时间越长，相应的停车次数也越大，则外部抑制剂越大;延误时间越长，相应的通行能力越小，在双抑制原理作用下，其他相位的绿灯时间将会减少。BDILDA通过激发剂和双抑制剂调整各信号相位的绿灯时间完成时间分配，具有原理简要明晰、便于实现的特点。

双抑制原理需要对激发剂、内部抑制剂和外部抑制剂进行比较，但是目前交通配时研究中多采用延误时间、停车次数还有最大通行能力的绝对值，这些参数各性能指标的量纲和量级都不同，导致各指标权重模型的物理意义不明确，或因某个指标量级过大使目标函数无量纲化和克服性能指标的量级差异难以直接比较。这里以经典F-B配时法的控制方案（TRRL）对应的延误时间、停车次数還有最大通行能力为标准数，建立相对性能指标。

第i相位车辆通行能力的相对指标为：

其中n为信号相位的个数，这里假设蜜蜂与所有蜜蜂都进行交互。

双抑制原理是通过激发剂、内部抑制剂和外部抑制剂之和的比（后面简称激发抑制比）来控制蜜蜂的生理年龄。相应地，在BDILDA中，通过激发抑制比来决定信号相位的绿灯时间，具体如下：

其中：dhigher为激发抑制比的上限阈值，dlower为激发抑制比的下限阈值，xi为相位i的绿灯时间，σi为绿灯时间变化量。当激发抑制比大于上限阈值时，绿灯时间增加;当激发抑制比低于下限阈值时，绿灯时间减小;当激发抑制比大于下限阈值且小于上限阈值时，绿灯时间不变。

其中：当激发抑制比大于上限阈值时，绿灯时间变化量为正相关;当激发抑制比低于下限阈值时，绿灯时间变化量为负相关;当激发抑制比大于下限阈值，小于上限阈值时，绿灯时间变化量不变。

为进一步提高算法效率，在每一次时间分配过程中，对各相位绿灯时间的变化量进行如下修正：当所有相位都选择减小绿灯时间时，以最大减少量作为总的减少量，并按照减少比例分给各相位，此时信号周期变短;当所有相位都选择增加绿灯时间时，以最大增加量作为总的增加量，并按照增加比例分给各相位，此时信号周期变长;当一部分相位选择增加绿灯时间，而另一部分相位选择减小绿灯时间时，通过归一化处理，使得时间的增加量等于时间的减少量，此时信号周期保持不变;当所有相位都选择保持绿灯时间不变时，算法达到停止准则。

BDILDA在解决交通信号配时问题时，每个信号相位都有增加绿灯时间、减小绿灯时间和保持绿灯时间不变三种行为选择。具体选择哪一种行为，是由信号相位的激发抑制比决定的，其中的激发剂与信号相位自身的延误时间有关，内部抑制剂与信号相位自身的通行能力有关，外部抑制剂与其他信号相位的停车次数有关。信号相位的激发剂、抑制剂和激发抑制比会随着绿灯时间、交通流量以及信号周期等变化，使得同一信号相位在不同交通场景下的行为选择不同，进而能够适应环境的变化。

为了提高算法的运行效率，本文在调整信号相位绿灯时间的时候按照以下标准进行设置：当交叉口信号相位的绿灯时间都选择增加的时候，以最大增加量作为标准增加总的信号周期，同时增加量按照不同的比例分配给不同的信号相位;当交叉口信号相位的绿灯时间都选择减少的时候，以最大减少量作为标准减少总的信号周期，同时减少量按照不同的比例分配给不同的信号相位;当交叉口一部分信号相位的绿灯时间选择增加，而另一部分信号相位的绿灯时间选择减少的时候，此时信号相位的总周期保持不变，通过归一化处理，让绿灯时间的增加量等于绿灯时间的减少量;当交叉口信号相位的绿灯时间保持不变的时候，算法达到停止条件。

BDILDA在求解信号配时问题时，根据信号相位的激发抑制比，每个信号相位都有减少绿灯时间、增加绿灯时间和保持绿灯时间不变三种不同的行为选择。其中激发剂与信号相位自身的延误时间有关，内部抑制剂与信号相位自身的通行能力有关，外部抑制剂与其他信号相位的停车次数有关。信号相位的激发剂、内部抑制剂、外部抑制剂和激发抑制比会随着交通流量、绿灯时间以及信号周期等变化，使得信号相位能够根据不同的交通场景选择不同的行为，从而能够适应动态变化的交通环境。

下面描述了BDILDA的具体实现步骤：

步骤1 数值初始化。配时参数以及算法参数，包括相位总数n、信号周期C、绿灯时间x、最大迭代次数N、上限阈值dhigher、下限阈值dlower、内部抑制剂系数α、绿灯时间变化量σ0等，转步骤2。

3.1 实验背景

本文使用的交通数据来自于2014中国“云上贵州”大数据商业模式大赛——智能交通算法大挑战（http：//www.et-data.com/index.html）。该数据描述了若干天内，贵阳市南明区的主干路段06：00—20：00时间段内通过各交叉路口的车流量情况。其中，车流量是每个时间单位T的车辆数n。T指的是：把一天（6：00—20：00）的时间离散化，每30s作为一个时间单位T。如：记录“tl3，tl36，0，…，25，26，21，26，27，29，28，32，24，18，20，21，…，8”表示：从tl36红绿灯到tl3红绿灯这个路段，在从早上6点到晚上8点的时间里，每30s内的车辆数一次为0，…，25，26，21，26，27，29，28，32，24，18，20，21，…，8。图5中红绿灯用tli来表示。本文选取交通数据文件“flow0901.txt”中红绿灯ID为“tl23”的交通数据车流量变化较明显，对于评估信号配时方法的效果具有较强的说服力。通过处理得到红绿灯“tl23”在该天车流量的情况如图6所示。

实验中所涉及的参数设置如下：假设车辆在交叉口处直行、左转和右转的比例分别为60%、20%和20%，相应的直行车道、左转车道和右转车道的饱和流量分别为1500pcu/h、1200pcu/h和1200pcu/h。交叉口綠灯间隔时间为4s，黄灯时间为3s，启动损失时间为3s，最短绿灯时间为15s，最长绿灯时间为90s。上限阈值dhigher为1.2、下限阈值dlower为0.6、内部抑制剂系数α为1、绿灯时间变化量σ0为1，最大迭代次数N为100。

3.2 对比实验

为了验证本文算法（BDILDA）的有效性与先进性，本节采用4种典型的算法进行对比分析，分别是传统的Webster算法[5]、群智能多种群蚁群算法（Multi-Colony Ant Algorithm， MCAA）[7]、迁移蜂群（Transfer Bees Optimizer， TBO）算法[21]和近年来新出现的反向烟花算法（Backward FireWorks Algorithm， BFWA）[22]。求解时，先用Webster方法估计初始周期，然后利用等饱和比的方法计算各相位的大致信号配时，再用BDILDA进行分配求解。上述4种算法的计算结果如表1。

3.3 实验结果分析

由表1的计算结果可以得知，双抑制算法优化结果的延误时间、平均停车次数以及路口通行能力在4组测试实验中都优于Webster算法、多种群蚁群算法、迁移蜂群算法和反向烟花算法。其中在延误时间方面，本文算法相对其他算法能减小平均延误时间16.1%、18.2%、20.1%和14.3%;在停车次数方面，本文算法相对其他算法能减小平均延误时间4.5%、4.4%、3.7%和3.8%;在最大通行能力方面，本文算法相对其他算法能增大最大通行能力17.3%、7.5%、5.2%和23.6%。同时在计算时间方面，本文算法求解效率最高，算法计算时间能大幅缩短，相对于迁移蜂群算法能提高计算效率2.08倍，相对于多种群蚁群算法能提高计算效率2.02倍、相对于反向烟花算法能提高计算效率1.44倍。计算效率是迁移蜂群算法的2.08倍，多种群蚁群算法的2.02倍，反向烟花算法的1.44倍。

此句的表述不清晰，是否可以改为“计算效率是迁移蜂群算法的2.08倍，多种群蚁群算法的2.02倍，反向烟花算法的1.44倍”

由圖6可以看出，交叉口流率比从早上6：00开始上升，在早上9：00到达峰值，然后一直下降。从图7可以看出，随交叉口流率比的增加，平均停车次数增加，最大通行能力先增加后下降，延误时间先增加后下降，从而使得控制目标在路口闲散状态下侧重减小延误时间和停车次数，而在拥堵状态下则侧重减小延误时间和提高通行能力。通过这种方式实现不同交通状态下交通路口管理效能最大化。

BDILDA作为求解交通配时问题的方法，在求解中用Webster方法估计初始上下限，保证了群智能劳动分工中各个个体任务分配在约束区间内，并与双抑制算法的激发抑制比的上下限来比较，很大程度上提高了计算效率。

在求解交通配时问题中，Webster算法、多种群蚁群算法、迁移蜂群算法和反向烟花算法等智能算法是建立在复杂的人工优化模型的基础上进行计算，而这类提前设定好的模型大都难以应对剧烈变化的交通环境，BDILDA作为求解交通配时问题的方法，该算法继承蜂群劳动分工特点，以任务动态分配的方式完成信号时间的分配，在求解中用Webster方法估计初始上下限，保证了群智能劳动分工中各个个体任务分配在约束区间内，并与双抑制算法的激发抑制比的上下限来比较，很大程度上提高了计算效率。

4 结语

本文面向复杂系统中的任务分配问题，对以往的智能优化算法进行了回顾，分析了不足之处;对蜂群劳动分工现象进行了研究，提出一种面向交通信号配时问题的蜂群双抑制劳动分工算法（BDILDA），并在有代表性的单交叉口交通信号配时中进行了建模应用，与传统智能优化算法展开了多方面对比，获得了良好的效果。本文的主要结论归结如下：

1）通过对蜂群劳动分工的深入研究，提出了一种基于群智能的蜂群双抑制劳动分工算法（BDILDA）。通过个体内部抑制剂和外部抑制剂的相互作用，动态调节群体的劳动分工。该方法自组织程度高，反应快，具有更强的分配柔性和高效性，是一种全新的群智能算法。

2）通过分析蜂群劳动分工和信号配时的特点，给出了劳动分工与信号配时之间的映射关系。该算法与其他算法在实际交通情景下的实验结果表明，BDILDA展现出明显的有效性，适于求解不确定环境下的动态分配问题

3）BDILDA是一种有效的动态自组织任务分配方法，具有适应动态环境变化的能力，该算法为解决十字交叉口交通信号配时问题以及其他的任务分配问题提供了一种新颖有效的解决思路和方法。

下一步的研究重点分两个方面：1）深入分析BDILDA模型的激发抑制机制，激发剂相当于正反馈作用，内部抑制剂和外部抑制剂相当于负反馈作用，提出更加方便、实用的双抑制劳动分工模型，进一步提高BDILDA的性能。2）将BDILDA应用到其他分配问题中去。

随着研究的进一步深入，这种新一代的仿生类算法将在交通规划与控制领域，如动态交通分配、复杂多交叉口系统配时等方面发挥更大的作用。

参考文献 （References）

[1] ZHAO D， DAI Y， ZHANG Z. Computational intelligence in urban traffic signal control： A survey [J]. IEEE Transactions on Systems， Man， and Cybernetics， Part C （Applications and Reviews）， 2012， 42（4）： 485-494.

[2] 肖人彬，陶振武.群集智能研究进展[J].管理科学学报，2007，10（3）：80-96.（XIAO R B， TAO Z W. Research progress of swarm intelligence [J]. Journal of Management Sciences in China， 2007， 10（3）： 80-96.）

[3] BESHERS S N， FEWELL J H. Models of division of labor in social insects [J]. Annual Review of Entomology， 2015， 46： 413-440.

[4] WUNDERLICH R， LIU C， ELHANANY I， et al. A novel signal-scheduling algorithm with quality-of-service provisioning for an isolated intersection [J]. IEEE Transactions on Intelligent Transportation Systems， 2008， 9（3）： 536-547.

[5] 翟润平，周彤梅.道路交通控制原理及应用[M].北京：中国人民公安大学出版社，2002：12-56.（ZHAI R P， ZHOU T M. The Theory and Application of Road Traffic Control [M]. Beijing： Publishing House of Chinese Peoples Public Security University， 2002： 12-56.）

[6] 徐勋倩，黄卫.单路口交通信号多相位实时控制模型及其算法[J].控制理论与应用，2005，22（3）：413-416.（XU X Q， HUANG W. Multiphase traffic signal real-time controlling model of isolated intersection and its algorithm [J]. Control Theory and Applications， 2005， 22（3）： 413-416.）

[7] 伍尚昆，陈翠宜，祝胜林.基于多种群蚁群算法的交叉路口信号配时优化[J].计算机应用与软件，2014，31（5）：83-88.（WU S K， CHEN C Y， ZHU S L. Timing optimisation for intersection signal based on multi-colony ant algorithm [J]. Computer Applications and Software， 2014， 31（5）： 83-88.）

[8] 曹陽.基于模拟退火的交叉口自适应信号控制优化研究[J].交通运输工程与信息学报，2018，16（1）：49-55.（CAO Y. Optimization of adaptive signal control using simulated annealing algorithm [J]. Journal of Transportation Engineering and Information， 2018， 16（1）： 49-55.）

[9] 王建宇，彭维，王康平，等.增强学习与神经网络在交通信号控制中的应用[J].计算机工程与应用，2007，43（31）：242-244.（WANG J Y， PENG W， WANG K P， et al. Application of reinforcement learning and neural network in traffic signal control [J]. Computer Engineering and Applications， 2007， 43（31）： 242-244.）

[10] CHIN Y K， YONG K C， BOLONG N， et al. Multiple intersections traffic signal timing optimization with genetic algorithm [C]// Proceedings of the 2011 International Conference on Control System， Computing and Engineering. Piscataway， NJ： IEEE， 2011： 454-459.

[11] DEEPA O， SENTHILKUMAR A. Swarm intelligence from natural to artificial systems： ant colony optimization [J]. International Journal on Applications of Graph Theory in Wireless Ad Hoc Networks and Sensor Networks， 2016， 8（1）： 9-17.

[12] 琚春华，陈庭贵.基于能力评价与利益驱动的扩展蚁群劳动分工模型及在动态任务分配中的应用[J].系统工程理论与实践，2014，34（1）：84-93.（JU C H， CHEN T G. Extended labor division model of ant colony based on ability-evaluation and interest-driven and its applications in dynamic task allocations [J]. Systems Engineering—Theory and Practice， 2014， 34（1）： 84-93.）

[13] 阎静，曾建潮，张国有.基于劳动分工的群机器人地图创建探索策略研究[J].计算机应用研究，2013，30（1）：94-98.（YAN J， ZENG J C， ZHANG G Y. Research on exploration strategy in map building of swarm robotics based on model of division of labor [J]. Application Research of Computers， 2013， 30（1）： 94-98.）

[14] DORIGO M， BONABEAU E， THERAULAZ G. Ant algorithms and stigmergy [J]. Future Generation Computer Systems， 2000， 16（8）： 851-871.

[15] WU H S， LI H， XIAO R B， et al. Modeling and simulation of dynamic ant colonys labor division for task allocation of UAV swarm [J]. Physica A： Statistical Mechanics and its Applications， 2018， 491： 127-141.

[16] BONABEAU E， DORIGO M， THERAULAZ G. Inspiration for optimization from social insect behavior [J]. Nature， 2000， 406（6791）： 39-42.

[17] SEELEY T D， KOLMES S A. Age polyethism for hive duties in honey bees-illusion or reality？ [J]. Ethology， 1991， 87（3/4）： 284-297.

[18] SULLIVAN J P， JASSIM O， FAHRBACH S E， et al. Juvenile hormone paces behavioral development in the adult worker honey bee [J]. Hormones and Behavior， 2000， 37（1）： 1-14.

[19] AMDAM G V， OMHOLT S W. The hive bee to forager transition in honeybee colonies： the double repressor hypothesis [J]. Journal of Theoretical Biology， 2003， 223（4）： 451-464.

[20] NAUG D， GADAGKAR R. Flexible labor division mediated by social interactions in an insect colony—a simulation model [J]. Journal of Theoretical Biology， 1999， 197（1）： 123-133.

[21] 徐茂鑫，张孝顺，余涛.迁移蜂群优化算法及其在无功优化中的应用[J].自动化学报，2017，43（1）：83-93.（XU M X， ZHANG X S， YU T. Transfer bees optimizer and its application on reactive power optimization [J]. Acta Automatica Sinica， 2017， 43（1）： 83-93.）

[22] 李浩，柏鹏，张辉，等.反向烟花算法及其应用研究[J].西安交通大学学报，2015，49（11）：82-88.（LI H， BAI P， ZHANG H， et al. Backward fireworks algorithm and application research [J]. Journal of Xian Jiaotong University， 2015， 49（11）： 82-88.）