长江中游水路货运量与GDP及运输结构动态关系分析

2019-09-04胡仲达张培林卢文昌张佳楠

物流技术 2019年8期

胡仲达，张培林，卢文昌，曹莹，张佳楠

（武汉理工大学交通学院，湖北武汉 430063）

1 引言

长江是货运量位居全球内河第一的黄金水道，是我国东西交通运输的大动脉。长江中游承东启西、沟通南北，是长江综合立体交通走廊的关键区段，腹地内湖北、湖南和江西三省经济社会、货运量快速增长，1995-2017年区域水运量从8 740万t增长到70 195 万t，年均增长率9.93%。随着国家长江经济带、“一带一路”等区域战略的实施，经济格局由东向西梯度转移加快，提升了长江中游区域的战略地位、承东启西的区位功能和经济发展潜力，对中游航运整体保障水平和重点支撑能力提出了新的更高要求。因而需要科学认知长江中游区域水运量与GDP及运输结构的动态变化关系，为制定长江中游航运发展和航道治理规划提供可靠的依据。

对于货运量与其影响因素的关系研究，通常以VAR模型[1]为主进行分析，如耿波（2014）以VAR模型为基础，分析了中国货运量与GDP 及运输结构的动态关系[2]，吕稼欢和范文强（2016）重点分析重庆市交通运输需求与经济之间的关系[3]，周志龙（2011)以综合运输交通方式为核心，研究我国经济发展、产业结构与交通运输结构发展的变化关系[4]。从已有研究看，甚少涉及长江中游水运量和GDP及运输结构的变化关系研究。本文构建VAR模型，研究区域GDP、运输结构对长江中游水路货运量的影响，研究表明：长江中游区域水路货运量与GDP和运输结构之间存在长期均衡关系，且都是长江中游水路货运量变化的Granger 原因，GDP 和运输结构对长江中游水路货运量的长期弹性分别为0.9186和0.1602，即GDP发展对长江中游水路货运量的影响大于运输结构的影响。

2 VAR模型构建

VAR 模型又称向量自回归模型，是一种常用的计量分析模型。由Christopher Sims 于1980年提出，该模型不以经济理论为基础，不带有任何事先约束条件，用当期变量对所有变量的滞后变量进行回归，用来估计联合内生变量的动态关系。其利用数据的统计性质，把系统中每一个内生变量作为所有内生变量滞后值的函数来构造模型，从而将单变量自回归模型推导成由多元时间序列变量组成的“向量”自回归模型。

2.1 数据处理

长江中游区域以湖北、湖南和江西三省为代表，研究区域水路货运量与GDP 及运输结构的变化关系，收集了1995-2017年该区域GDP、货运总量和水路货运量相关数据，具体见表1。

设长江中游区域水路货运量为被解释变量，用SYL表示；区域GDP和运输结构为解释变量，分别用GDP和YSJG表示，其中运输结构指区域水路货运量占货运总量的比例；为使变量呈线性趋势，对区域水路货运量、GDP和运输结构取自然对数，得lnSYL、lnGDP和lnYSJG，此处理并不改变原有变量的协整关系。

2.2 平稳性检验

构建VAR模型，需检验数据序列的平稳性，因为时间序列中普遍存在非平稳的数据，直接回归可能会出现“伪回归”现象。本文采用ADF单位根检验法对各变量进行平稳性检验，进行ADF单位根检验时，若ADF 检验值大于所有水平下的临界值，则变量存在单位根，即具有不稳定性；若ADF检验值小于任意水平下的临界值，则变量不存在单位根，即具有稳定性。本文使用Eviews 软件对lnSYL、lnGDP 和lnYSJG进行平稳性检验，检验结果见表2。

表1 长江中游区域相关数据

表2 ADF单位根检验结果

由表2可知，lnSYL 的 ADF 检验值小于 10%临界值，lnSYL 在10%显著水平下平稳，lnGDP 在5%和10%显著水平下平稳，lnYSJG 在10%显著水平下平稳，即lnSYL、lnGDP和lnYSJG都具有稳定性，因而可以在此基础上构建VAR模型和进行协整检验。

2.3 VAR模型

在lnSYL、lnGDP和lnYSJG的原序列平稳和确定合适的滞后期后，可直接建立VAR 模型。一般根据AIC赤池信息准则和SC准则取值最小的原则来确定模型的滞后阶数，本文以此确定的最佳滞后阶数为4，建立VAR模型，结果如下：

3 模型检验与分析

3.1 Johansen协整检验

协整检验是在VAR 模型的基础上检验回归系数，其中Johansen协整检验是进行多个变量的协整检验方法，以检验非平稳序列的线性组合是否具有稳定的均衡关系[5]。

本模型有 lnSYL、lnGDP 和 lnYSJG 三个变量，需采用Johansen协整检验方法分析其协整关系，检验回归系数。序列lnSYL、lnGDP和lnYSJG之间的协整关系检验结果见表3和表4。

表3 迹统计量检验结果

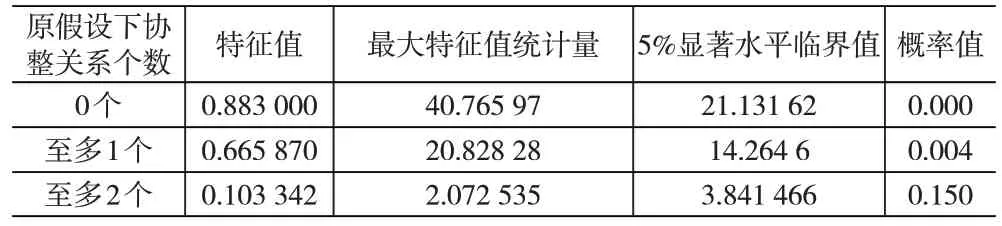
表4 最大特征值统计量检验结果

Johansen 协整检验结果表明，lnSYL、lnGDP 和lnYSJG之间存在2个协整关系，协整方程如下：

协整方程1：

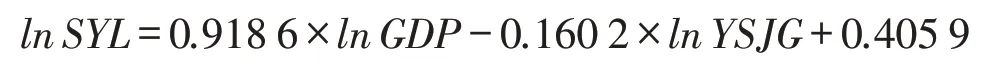
协整方程2：

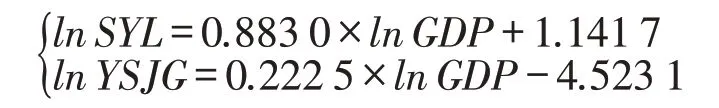
两个协整方程表明VAR 模型中的lnSYL、lnGDP和lnYSJG 之间存在长期均衡关系，GDP 和运输结构对长江中游水路货运量的长期弹性分别为0.918 6和0.160 2，GDP对长江中游水路货运量和运输结构的长期弹性分别为0.883 0和0.222 5，从长远来看经济发展对长江中游水路货运量的影响大于运输结构变化的影响。确认三者的协整关系后，可通过Granger 因果关系分析和脉冲函数分析进一步研究GDP和运输结构对长江中游水路货运量的影响是正向还是负向。

3.2 Granger因果关系分析

Granger因果关系检验是一种用来分析变量之间因果的方法，但其因果关系并非常规理解的因与果的关系，而是指一个变量的前期变化能有效解释另一个变量的变化。进行Granger 因果关系检验要求是回归式，要求时间序列变量具有平稳性，以避免伪回归。

由于本VAR模型中的lnSYL、lnGDP和lnYSJG三者之间存在着长期均衡关系，表明三者至少存在一个方向的因果关系。为研究三者具体的因果关系，对VAR模型进行Granger Causality检验，检验结果见表5。

表5 VAR模型的Granger Causality检验结果

由表5可知，GDP和运输结构都是水路货运量变化的Granger 原因，而水路货运量的增加还无法有效解释GDP 与运输结构发生的变化；GDP 变化与运输结构变化互成Granger 因果关系。这表明长江中游水路货运量的增长可以由长江中游区域GDP增长和运输结构的变化来有效解释，长江中游区域GDP 增长和运输结构的变化也可以相互解释。

3.3 脉冲函数分析

脉冲响应函数描述了一个内生变量的单位误差冲击对自身与其它内生变量带来的影响，或随着时间的变化，各个内生变量对于冲击的响应。在确定协整关系后，建立 lnSYL、lnGDP 和 lnYSJG 时间序列的VAR模型，得到AR根图，如图1所示。

图1 水平单位圆和特征根

由图1可知，特征方程全部根的倒数值都落在单位圆内部，表明模型稳定性较好，可以进一步对VAR模型进行脉冲响应函数分析，结果如图2所示。

图2 脉冲响应图

由图2可知，长江中游水路货运量对自身一个标准差新息立即做出响应，这种响应约为0.04，然后逐渐降低，到第9 期达到最低值，约为-0.04。随后上升，在第20期左右达到平稳。水路货运量对运输结构的一个标准差新息没有立即做出响应，在第1期响应为0，随后快速下降，在第2 期达到最小，约为-0.03，然后逐步上升，到第9 期达到最大，约为0.045，接着缓慢下降，在第18期逐渐趋于平稳，约为0.02。长江中游货运量对GDP 的一个标准差新息没有立即做出响应，在第1期响应为0，随后起伏上升，在第5期达到最大，约为0.05，之后缓慢的起起伏伏，但整体趋势下降，18 期以后，逐渐趋于平稳，约为0.015。

长江中游区域GDP 受到正冲击后，长江中游水路货运量快速增长，然后下降趋于稳定；而长江中游水路货运量在长江中游区域运输结构的冲击下，先是负向影响，随后上升，成为正向影响，之后缓慢下降并趋于稳定。短期来看，长江中游区域GDP 对长江中游水路货运量是正向影响，运输结构是负向影响。长期来看，长江中游区域GDP 与运输结构对长江中游水路货运量带来的是正向影响，印证了Granger 因果关系分析得到“长江中游区域GDP 和运输结构都是长江中游水路货运量变化的Granger 原因”的结论。