基于模糊神经网络的智能汽车轨迹跟踪研究*

张炳力，李子龙，沈 干，方 涛，曹聪聪，郑平平

（合肥工业大学汽车与交通工程学院，合肥 230009）

前言

对于智能汽车和无人驾驶技术，其核心内容是环境感知和循迹控制，二者紧密联系。环境感知系统由摄像头和激光雷达等传感器获取路况信息，循迹控制系统依获取的路况信息行驶。循迹任务包括路径规划和轨迹跟踪，由控制器做出决策指令并通过底层执行机构对车辆的行驶状态进行操作。轨迹跟踪包括纵向控制和横向控制两部分，纵向控制是在汽车的行驶方向上通过控制节气门开度或电机转速，调整汽车行驶速度，以保持和前后车及障碍物的安全行驶距离。横向控制是通过转向盘及转向轮，对汽车的行驶方向进行调整，使汽车可以按预期的路线行驶，同时保证稳定性和舒适性。

自上世纪80年代起，关于轨迹跟踪的研究，主要采用郭孔辉等［1］提出的最优预瞄控制理论，在短时间内将车辆的控制解耦，分别进行纵向速度跟随和横向车道保持。文献［1］中即是对车辆动力学进行解耦，分别研究纵向和横向的控制，进一步提出了基于模型预测控制（MPC）的轨迹跟踪控制方法。文献［2］中提出一类基于单点预瞄的驾驶员方向控制模型，结合汽车状态参数预测行驶轨迹，仿真结果具有良好的跟踪精度和鲁棒性。文献［3］中设计了一种最优预瞄控制器，以预瞄时间内车辆行驶的偏差，预瞄点偏差和控制时间为二次性能指标函数，并用仿真和试验证明控制器的有效性。文献［4］中将控制系统分为感知层、决策层和执行层，划分和制定若干工况控制策略，通过加速度或驱动力模型进行纵向状态的转换。文献［5］中在最优预瞄理论的基础上采用强鲁棒性的滑模控制方法，设计了一种轨迹跟踪横向控制器，并针对滑模控制的抖动问题设计增益切换，仿真结果表明该控制器具有良好的适应性。文献［6］中提出一种基于预瞄的智能循迹控制策略，将行驶参数作为模糊控制和神经网络控制器的输入，并通过样本训练，以仿真试验表明该策略的实现效果。文献［7］中在预瞄理论的基础上提出一种无需坐标变换的圆弧预瞄位置确定算法，仿真结果表明该算法效果良好，运算速度较快。文献［8］中提出了一种由期望航向偏差生成器及反馈控制两部分组成的智能车辆的路径跟踪横向控制系统。

本文中在研究驾驶员模型［9］的基础上，利用神经网络所具有的自学习能力强的优点，不依赖于对象的深层次知识特性，设计了一种基于BP（back propagation）神经网络的车辆行驶状态预测模型。并结合模糊控制所具有的控制规则和强鲁棒性等特点，设计一种基于模糊神经网络（fuzzy neural network）的车辆行驶控制模型并将预测模型的输出作为其输入，综合考虑轮胎侧偏特性等对整车动力学的影响，将智能汽车的纵、横向控制作为一个整体进行研究。

1 轨迹跟踪模型

1.1 车辆动力学分析

为预测和分析车辆未来时间内的运动轨迹，确定轨迹跟踪关键参数，建立它们的传递关系，本文中选用车辆的2自由度模型做动力学分析，如图1所示。该模型将汽车的前轮转角作为输入，不考虑俯仰以及侧倾的影响，且假设横向速度远小于纵向速度。

图1中，a为前轴到质心的距离，b为后轴到质心的距离，Fy1为前轮的侧向力，Fy2为后轮的侧向力，vx为纵向车速，vy为横向车速，β为质心侧偏角，ω为横摆角速度，δ为前轮转角。

1.1.1 车辆横向动力学分析

由图1可知，在车辆坐标系下，车辆的动力学方程为

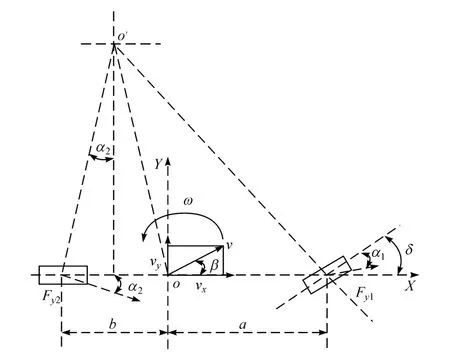
图1 车辆2自由度动力学模型

式中：m为整车质量；v·y为侧向加速度。

当轮胎处于线性区域时，侧向力和轮胎的关系为

式中：C1为前轮侧偏刚度；C2为后轮侧偏刚度；α1为前轮侧偏角；α2为后轮侧偏角。综合前、后轮侧偏角及转动惯量的定义，可得

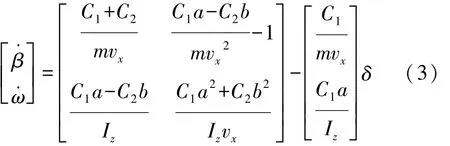
1.1.2 车辆纵向动力学分析

由图1及牛顿定律，车辆纵向动力学为

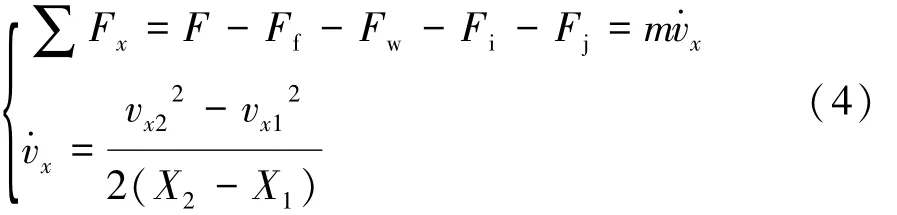
式中：F为驱动力；Ff为滚动阻力；Fw为空气阻力；Fi为坡度阻力；Fj为加速阻力；v·x为纵向加速度。

1.2 单点预瞄和轨迹跟踪模型

假设车辆在未来一段时间内以恒定的横摆角速度ω做稳态运动，选取合适的预瞄距离后，此时预瞄点和预测轨迹目标点上的横向距离称为侧向偏差［5］。由之前的分析即可得到转角和侧向偏差的传递函数，依此控制车辆跟随目标轨迹行驶。

同1.1节，在车辆坐标系下，描述车辆未来一段时间内运动状态的轨迹如图2所示。点G为当前车辆质心的位置，点P为目标轨迹上的预瞄点，XGP为预瞄距离，eL为侧向偏差，φ为航向角。

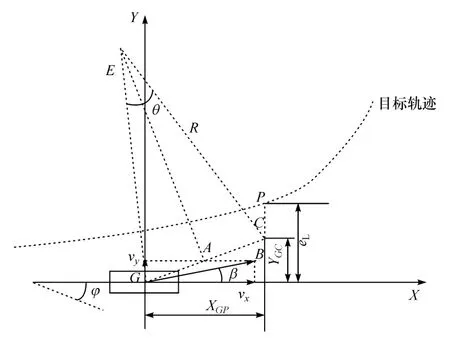
图2 单点预瞄车辆目标轨迹

车辆以恒定的横摆角速度从当前位置点G行驶到目标点P，由于横向速度vy远小于纵向速度vx，可认为车辆的合速度保持不变，且方向始终与其实际轨迹相切，此时汽车绕E做半径为R的圆周运动，圆心角为θ，C为经过预瞄时间后的质心位置。图2中，合速度方向与当前轨迹相切于坐标原点G，沿着GB方向。

当车速较低时，若预瞄距离过长会导致目标轨迹的信息利用不够充分，反之当车速较高时，预瞄距离过短则会引起信息获取不足［1］。由图2可知，预瞄时间tp为

在上文的假设条件下，车辆的运动可看作沿半径R的圆弧行驶，因此，期望横摆角速度ωd为

根据几何关系可得

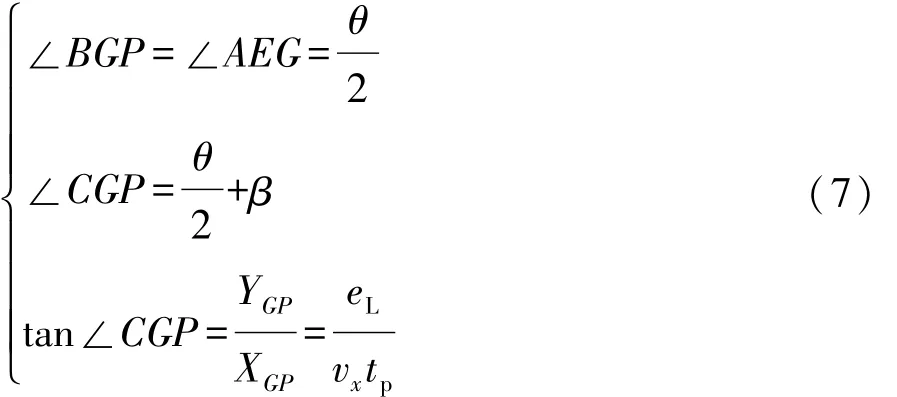
由此，可得

将上式代入式（6），并联立式（3）得到单点预瞄模型在动力学模型基础上补偿的转角［2］：

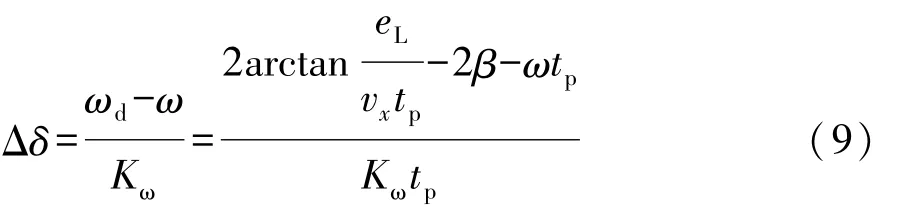
式中Kω为增量式转角补偿系数［2］。

由式（4）及式（5）可得单点预瞄模型的纵向车速为

综上各式，不难发现在轨迹跟踪的纵、横向控制中，主要的影响因素是经预瞄时间后质心位置的车速vC、预瞄点处的侧向偏差eL、质心侧偏角β和横摆角速度ω。

2 轨迹跟踪控制器

在以往研究横向控制相关的模糊控制［5］和神经网络［6］结构中，均假设纵向车速vx近似不变而不做处理，仅分析侧向偏差eL等参数对于转向盘转角或前轮转角的影响。本文中将为纵向车速vx设计BP神经网络并令其输出作为模糊神经网络的输入，把纵向分析的结果运用到横向控制上，从而提高轨迹跟踪的整体性和精确性。

针对1.2节中分析得到的影响因素，本文中所设计的智能汽车轨迹跟踪控制器如图3所示。图2中，车辆在当前位置点G的车速已知，而在预瞄时间后，质心C的车速未知，车辆行驶状态预测模型由车辆动力学得到纵向车速vx，将其数据做差分处理后输入神经网络，输出预测车速。由车辆动力学得到侧向偏差eL、质心侧偏角β和横摆角速度ω，并接受来自预测模型的纵向车速，最终控制器输出转向盘转角。

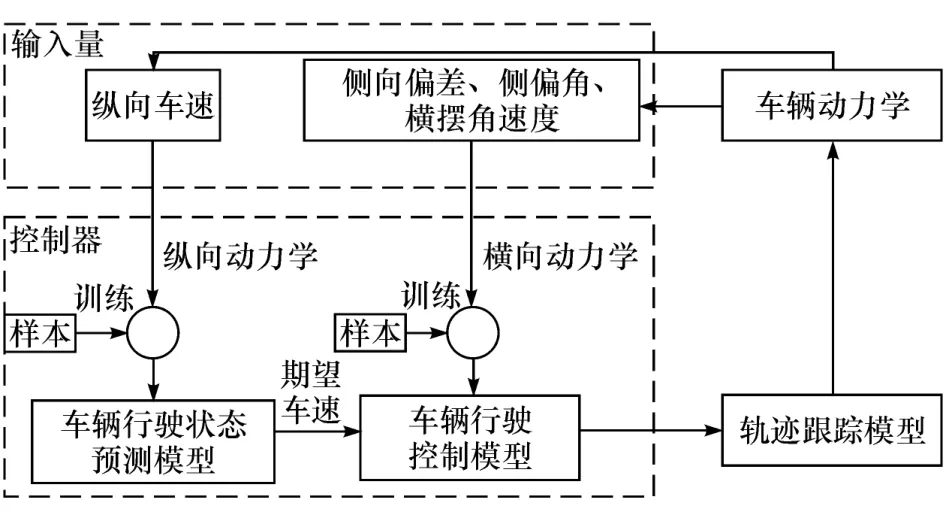
图3 智能汽车轨迹跟随控制器

2.1 车辆状态预测模型设计

神经网络可以依系统的复杂情况，改变内部神经元的相互关系，实现计算和处理功能。BP神经网络是一种前向神经网络，每层的神经元接收上一层作为输入，传递给下一层。

车辆行驶状态预测模型基于BP神经网络进行设计，分为输入层、隐含层和输出层，其结构如图4所示。

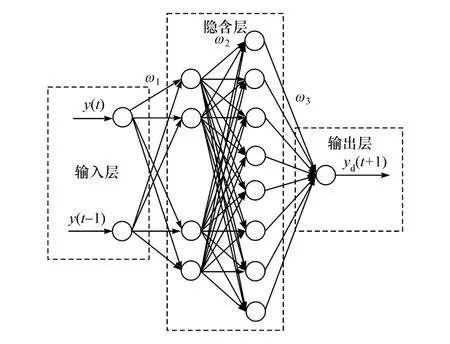
图4 车辆行驶状态预测模型网络结构

图中，y（t-1）和 y（t）是输入层神经元，分别为前一时刻状态和当前时刻状态；yd（t+1）是输出，为下一时刻的期望状态；ωi分别为各层的网络权值。在本文中所设计的预测模型中，以车辆前一时刻和当前时刻的纵向速度作为输入，经过BP神经网络训练后，输出下一时刻纵向速度期望值。

本预测模型的学习原理采用最速下降BP法，隐含层传递函数为Sigmoid函数，输出层传递函数为线性函数。误差函数定义为

采用串行方式调整网络权值，权值的误差反向传播方式为

式中：Δωij（n）为权值调整量；η为学习率；ζjJ为局部梯度；ζiI（n）为上一层的输出值。

2.2 车辆控制模型设计

模糊控制是一种结合了控制理论和模糊数学的智能控制方法，主要包括模糊集合化、模糊逻辑推理和模糊语言变量3个部分，但自身学习能力较差。神经网络则具有较强的自学习能力和信息分布式储存的特点，模糊-神经网络将模糊集合运用到神经网络中，能够很好地集二者优点于一身，特点体现在有监督的学习规则上。

车辆行驶控制模型基于逻辑模糊神经网络进行设计，其结构如图5所示。

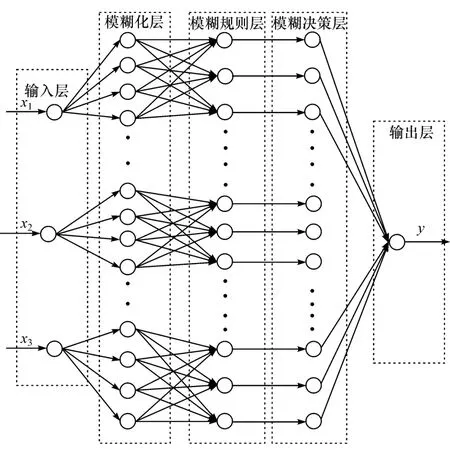
图5 车辆行驶控制模型网络结构

图中，控制模型的网络结构共分为5层，输入层、模糊化层、模糊规则层、模糊决策层和输出层。在本文中所设计的控制模型中，以侧向偏差、横摆角速度和纵向车速作为输入，以转向盘转角作为输出。

采用有监督的学习算法作为学习规则，误差函数定义和权值调整方式与预测模型相同。模糊语言值共5条：NB（负大）、NS（负小）、ZO（0）、PS（正小）和PB（正大），共产生53＝125条模糊规则。输入隶属度函数、解模糊化输出面和输入输出模糊集对应关系（部分）如图6所示。

3 仿真和试验

在MATLAB／Simulink中搭建前文中所述模型，并联合CarSim进行仿真试验和分析。

3.1 车辆预测模型的仿真和分析

模型中BP神经网络的训练样本经归一化后共2 000组，随机节选其中5组，如表1所示。

表1中数据已被归一化处理，故无单位（表2同）。对该模型输入样本进行训练，CarSim中设定车速为 45 km／h，加速度为 3 m／s2，分别进行仿真，以便对比。仿真结果如图7所示。

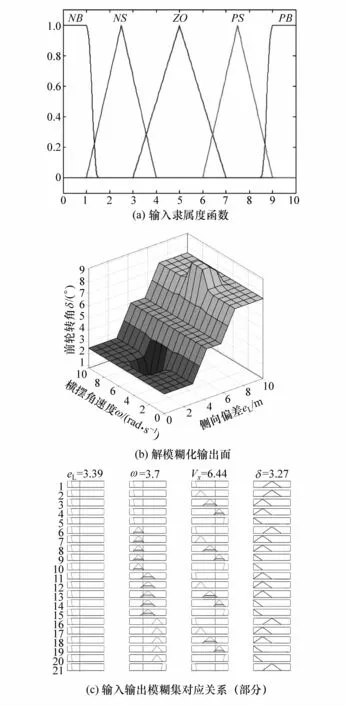
图6 控制模型模糊规则

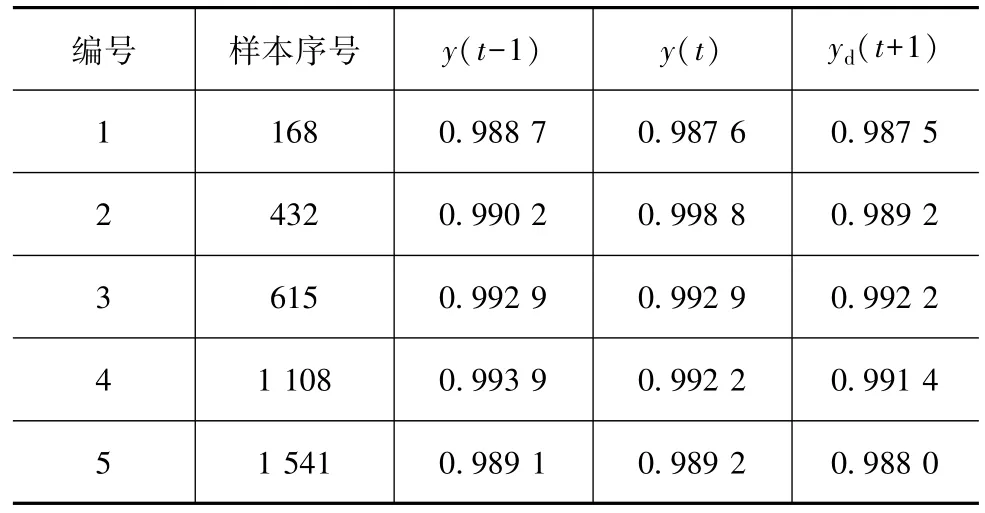
表1 预测模型训练样本

图7中，虚线为设定值，实线为模型仿真值。在输入样本训练后，本文中所设计预测模型的预测车速与仿真车速基本一致。输出的加速度值在设定值上下波动，后逐渐趋于稳定。可见，预测模型反映了神经网络具有学习能力强、收敛速度快的优点，且对车速预测准确，对加速度预测比较稳定、可靠。

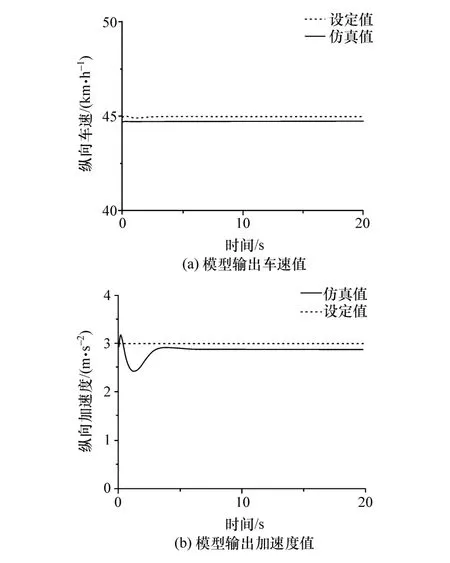
图7 预测模型仿真

3.2 车辆控制模型的仿真和分析

模型中模糊-神经网络的训练样本共4 000组，随机节选其中的5组，如表2所示。

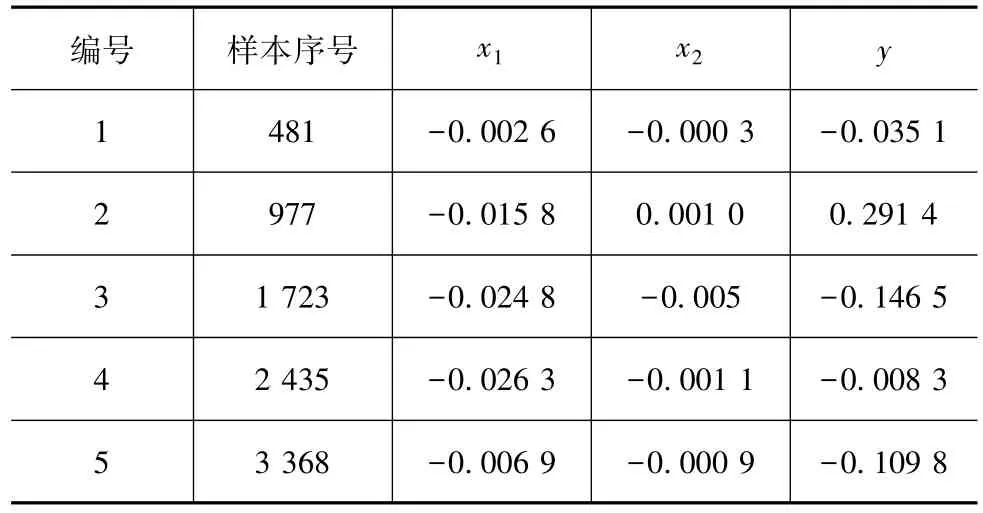
表2 控制模型训练样本

输入样本进行训练后，控制模型输出的结果和仿真对比如图8所示。

图中，实线为仿真值，虚线为模型输出值。由图可知，在输入样本进行训练后，在进入弯道的初始阶段和驶出弯道时的波动较明显，误差稍大，在弯道的横向控制中，本文中所设计的模糊-神经网络控制模型接收输入后对于转向盘转角的输出与仿真结果基本一致，可验证本模型的精确程度。

3.3 控制器的仿真和分析

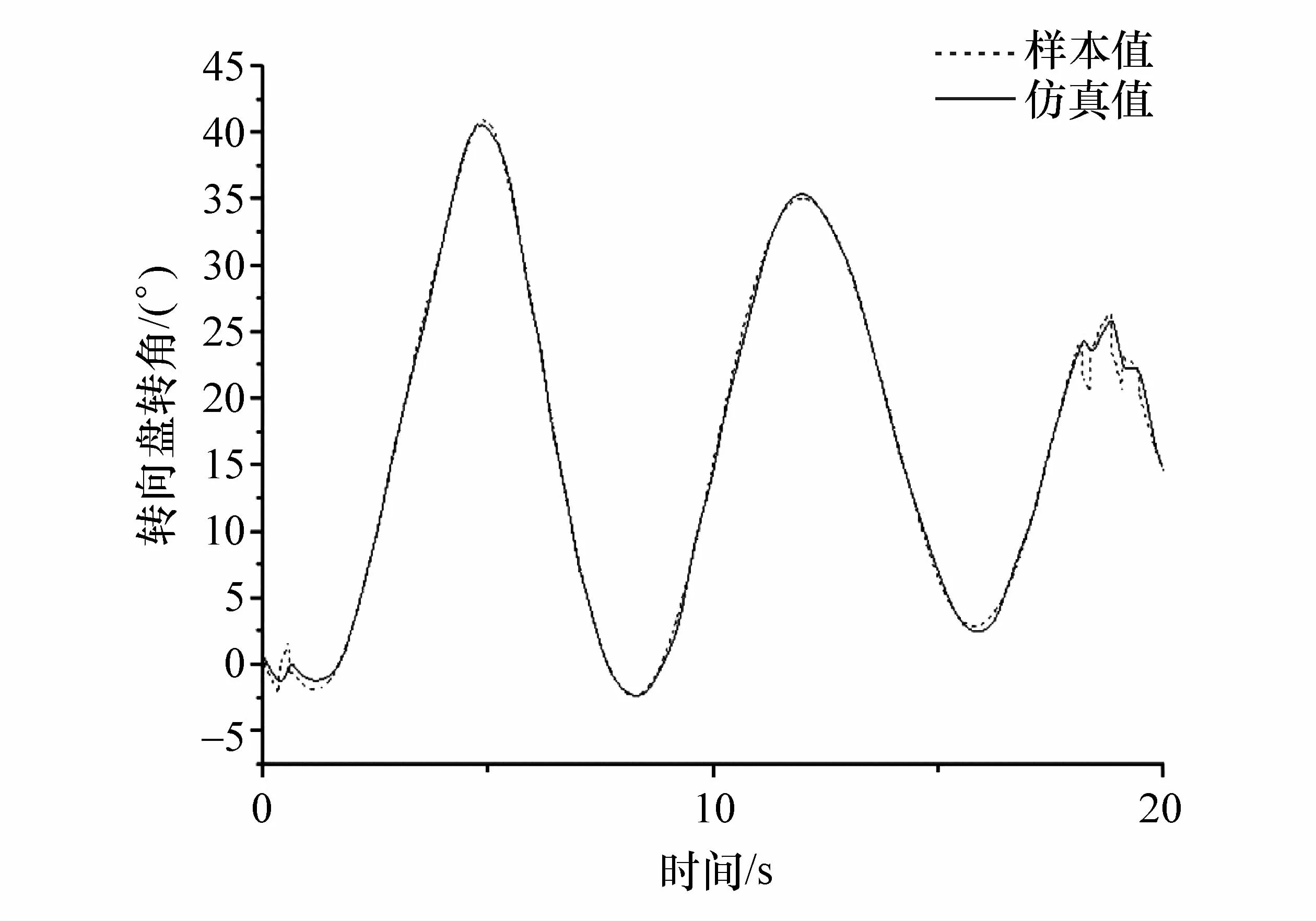
图8 控制模型仿真

仿真路径由直线和曲线组合而成，μ＝0.85，路径形状及在该路径下的轨迹跟踪仿真曲线如图9所示。

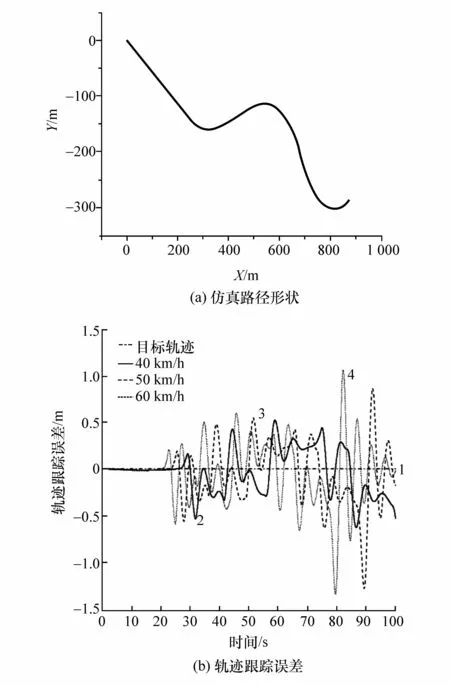
图9 轨迹跟踪仿真

图9 中，点划线1为目标轨迹，即为仿真路径的道路中心线，实线2为40 km／h车速下轨迹跟踪曲线，虚线3为50 km／h车速下轨迹跟踪曲线，点线4为60 km／h车速下轨迹跟踪曲线。由图可知，当车辆以较低的车速行驶时，以道路中心线为目标轨迹的轨迹跟踪在直道时相当精确，在弯道时误差较小，且转向控制对弯道路况反映迅速。当车速增加，循迹误差相应增大，误差波动较大。这是由于时滞等因素的影响，控制器对误差的修正不够及时，且当车速增加时这种现象愈发明显。

为验证本文中所设计的控制器对相关研究的改进，在与图9（a）相同的仿真路径上，分别基于模糊控制器和典型模糊神经网络控制器，搭建相应的模型，与本文中所设计的控制器在相同的仿真环境中进行对比，结果如图10所示。

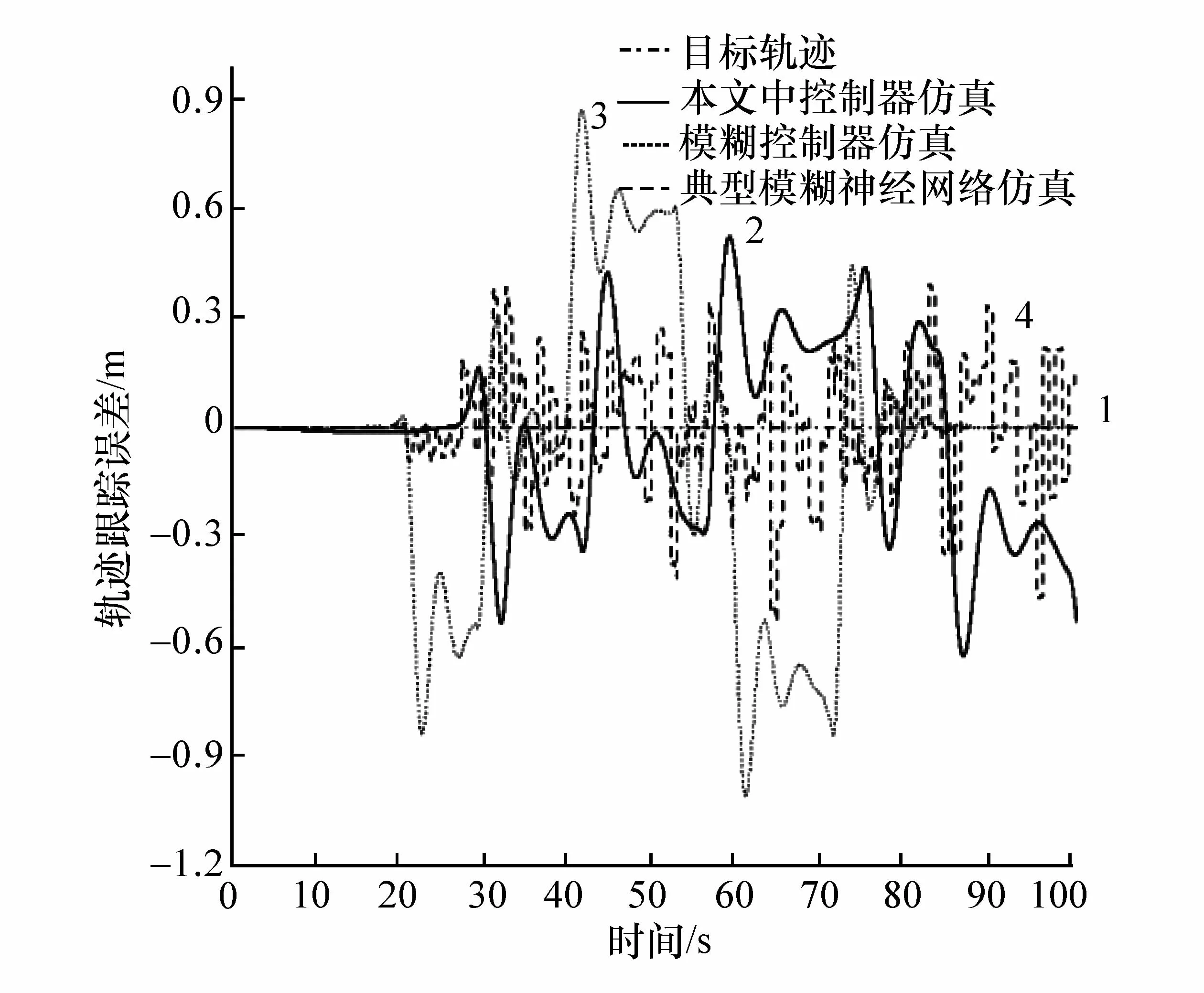
图10 不同控制器的仿真结果对比

图10 中，点划线1为目标轨迹，即为仿真路径的道路中心线，实线2为本文中控制器轨迹跟踪曲线，虚线3为模糊控制器轨迹跟踪曲线，点线4为典型模糊神经网络控制器轨迹跟踪曲线，仿真车速同为40 km／h。由图可知，相较于模糊控制，本文中所设计的控制轨迹跟踪精度有明显的提高，且更灵敏。相较于典型的模糊神经网络，本文中增加纵向车速作为输入，对于路径变化的感应明显更迅速，误差波动相对较小。

3.4 智能汽车试验

在校园路况下，依托课题组所开发的智能汽车进行实车试验。感知系统中所安装的激光雷达、毫米波雷达和视觉传感器能够确定前方路况信息，所搭建的RTK高精度定位系统和惯性导航系统能够确定实时的车辆状态。由传感器采集车速、加速度和转角等自车信息，在工控机中完成上述信息的融合。以CAN信号发送至上位机执行控制程序，由执行控制器进行底层操作。试验平台如图11所示，试验结果如图12所示。

图11 试验平台

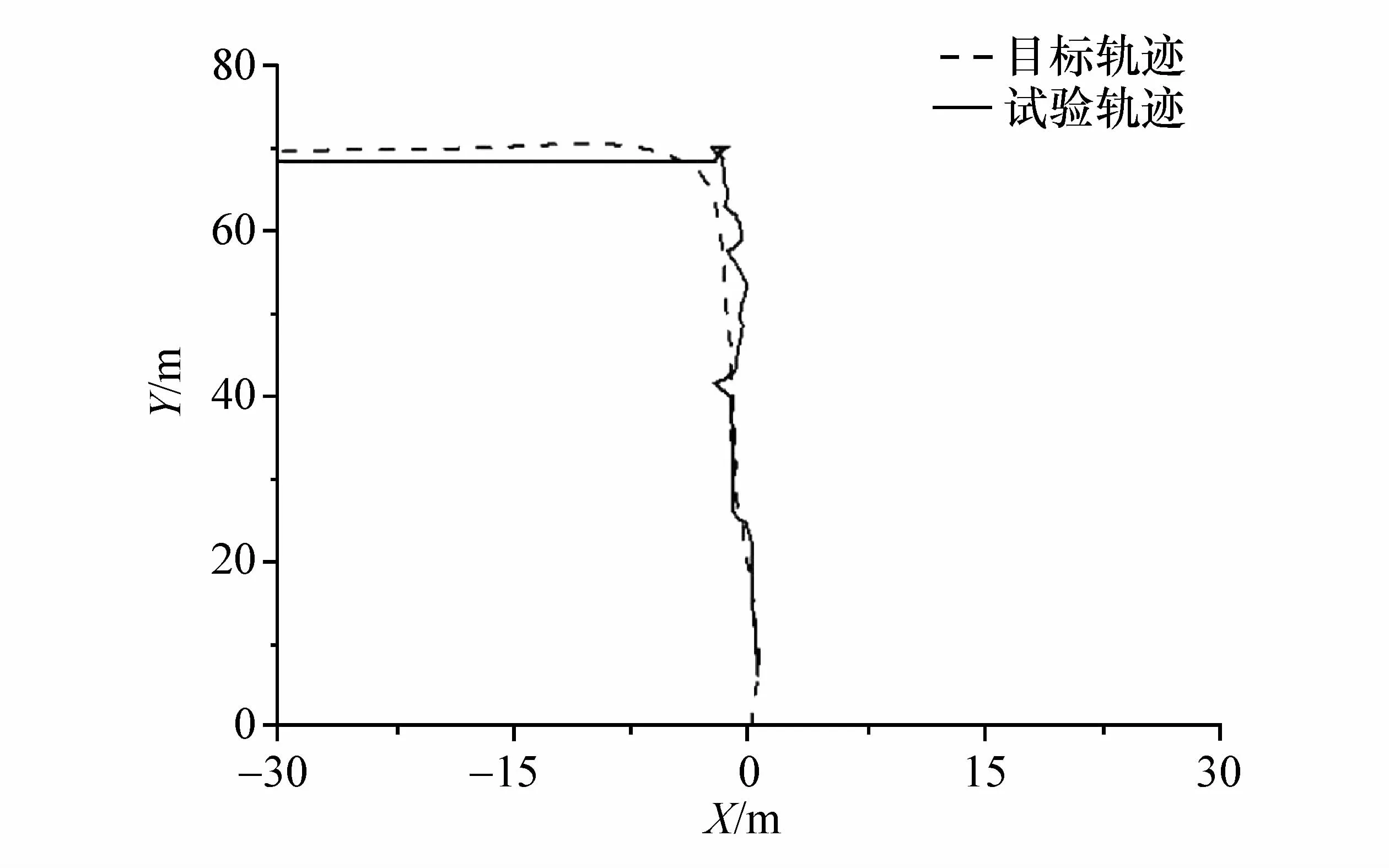
图12 试验结果

图12 中，虚线为试验标定采集到的校园道路中心线，即规划出的目标轨迹，实线为试验时的车辆行驶轨迹。从图中可以看出，车辆能够较好地依据规划路径进行跟踪，在直道时可以保持稳定的轨迹跟踪，但在弯道时出现转向操作的滞后，在弯道结束后进入直道的过程及进入直道后仍在进行修正，这一现象和上述仿真结果相吻合。

4 结论

（1）依据智能汽车轨迹跟踪原理，对车辆动力学进行研究，建立单点预瞄模型，分析纵向动力学和横向动力学控制，并据此确定轨迹跟踪控制中的主要影响因素。

（2）根据动力学分析结果，设计智能汽车轨迹跟踪控制器。针对轨迹跟踪控制中的关键参数，分别基于BP神经网络和模糊神经网络设计模型，确定了控制器架构和网络的结构及训练方式。

（3）在预测模型中将数据进行差分处理，得到输出，并把它与其它参数一同作为控制模型的输入，最终得到控制模型的输出。

（4）仿真和试验结果表明，所设计的智能汽车轨迹跟踪控制器较类似的工作有所改进，且在直道行驶及弯道较低车速行驶的情况下，能够达到较高的精度，并保持稳定，自适应能力强。在仿真和试验中出现转向控制不够及时的现象，且轨迹跟踪误差会随车速升高而增大，修正效果不够理想，需要进一步改善。