基于障碍物衍生状态格的智能车避障轨迹规划*

胡延平，田 博，陈无畏，张锐陈

（1.合肥工业大学机械工程学院，合肥 230009； 2.合肥工业大学汽车与交通工程学院，合肥 230009）

前言

根据行车路径规划算法的原理，将目前的轨迹规划算法归纳为两种：传统算法和智能算法。传统的路径规划算法有人工势场法［1-2］和启发式搜索算法（如 A*算法［3］，Dijkstra算法［4］，RRT算法［5］）等。其中文献［6］中对A*算法和Dijkstra算法从搜索速度和搜索效率进行比较。针对RRT算法很强的随机性，文献［7］中将人工势场法中引力的思想引入RRT算法中，提高了算法的实时性。智能算法主要有蚁群算法［8-9］、模糊逻辑算法［10］、神经网络算法和遗传算法［11-12］等。另外，对于整体的半结构环境中，文献［13］中通过 Bézier曲线［14］提出了在静态规划和动态障碍规划之间切换的路径规划方法。

状态格（state lattice）是由 Kelly和 Pivtoraiko［15］提出的一种将离散图嵌入到连续机器人配置空间中的路径规划方法。Madas等［16］曾将此方法与其他方法进行分析比较。Kushleyev等［17］在该算法的基础上考虑障碍物的运动不确定性，将短期轨迹规划和无时间量的路径规划结合。本文中针对动态障碍物，以障碍物的状态为出发点建立衍生状态格，通过设定S格成本，结合搜索算法处理多障碍物条件下的最优轨迹规划问题，与常规的栅格法相比无须对整个环境进行网格划分。最后通过仿真试验和硬件在环试验对该算法的可行性和有效性进行了验证。

1 衍生状态格的概念

在实际换道过程中对障碍车辆和自车进行矩形包裹。衍生状态格（下面简称S格）是由障碍物和避障车辆衍生的矩形方格，其尺寸同自车尺寸，其位置和状态参数由障碍物确定，如图1所示。

图中：C，Z和S分别表示避障车辆、障碍物和S格；S1和S2分别由障碍物Z1和Z2衍生所得。障碍物和对应S格的速度相等，即vz＝vs，S格和自车宽度相等即Ws＝Wc。W1为S格与障碍物相邻侧的垂直距离，W1数值的设定如图2所示。

图中：等效前轮转角为γ，两前轮转角为α和β；l和 lr分别为轴距和后悬值。若刚好达到不碰撞效果，则满足如下关系式：

图2 W1数值的确定

由式（1）可知，在避免碰撞的前提下，W1的最小尺寸由两前轮最大转角决定，在路径规划中将W1作为定值。障碍物与对应S格距离Wzs表达式为

Wzs＝（Wz+Ws）／2+W1

S格创建完成后，因为自车与S格位置重合时可保证避障车辆与障碍物间碰撞的可能性为零，故避障轨迹便是在自车和S格之间规划。

2 基于S格的避障轨迹规划算法

2.1 正反梯形约束的横摆角加速度模型

车辆换道采用非线性横摆角参考模型，满足正反梯形约束的横摆角加速度模型［18］，采用车辆换道时期横摆角加速度·θ·的参考模型如图3所示。

图3 期望横摆角加速度参考模型

图中 θdm为最大横摆角加速度，令时间满足：tbta＝td-tc＝te-td＝tg-tf＝ti-th＝tj-ti＝tl-tk＝T1，同时tctb＝tf-te＝th-tg＝tk-tj＝T2。为路径规划时计算方便，令T2＝5T1。车辆期望横摆角加速度模型和期望横摆角参考模型可用数学表达式表示如下：

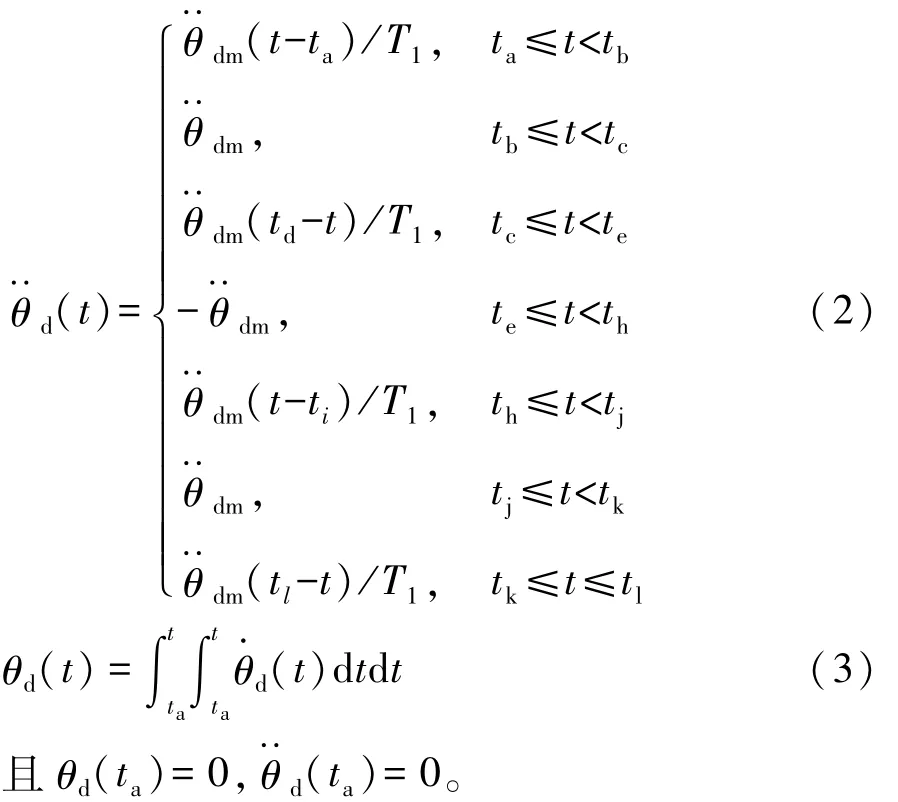
设避障轨迹为Sb，同时Sbx和Sby分别为避障轨迹沿着车道方向和垂直车道方向上的投影长度，其中Sby即为自车和S格的横向距离，满足：

2.2 单障碍物避障轨迹规划

2.2.1 直道路况

以避障车辆起始横向避障控制时质心的位置为坐标原点，建立相对地面静止的直角坐标系。单障碍物下，根据S格定义，根据道路宽度可产生最多两个可行S格，示意图如图4所示。

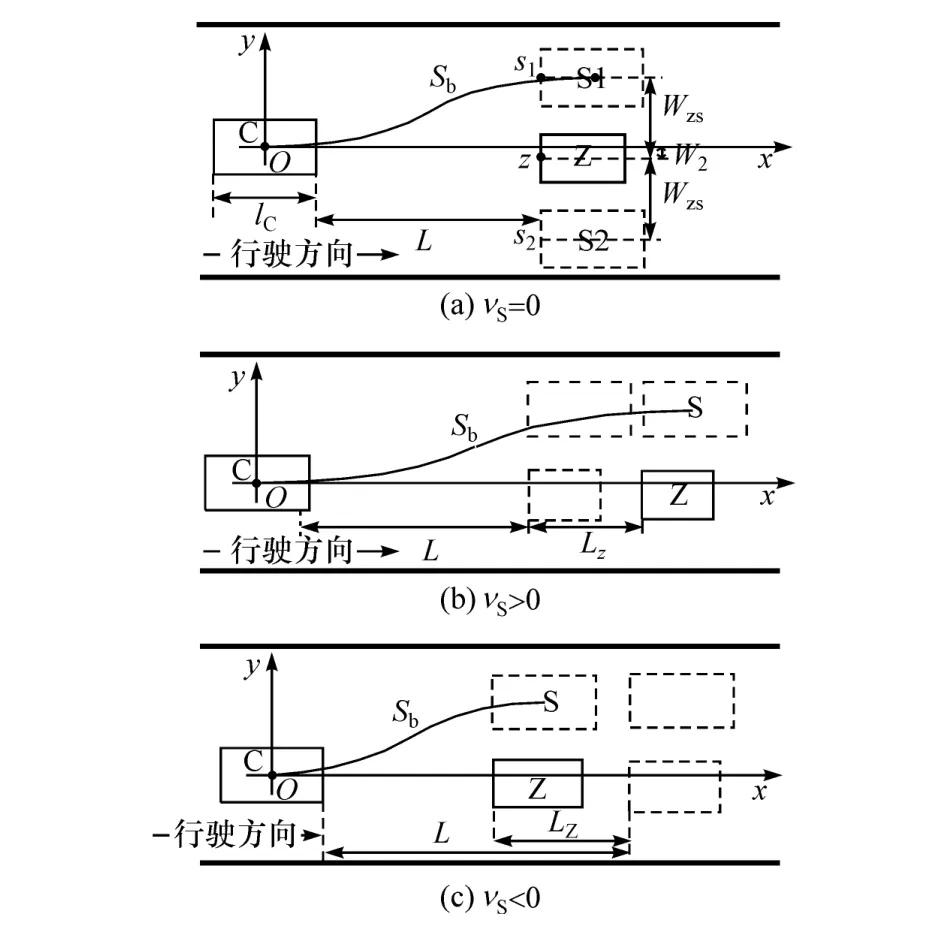
图4 直道S格创建示意图

图4 中W2和Wzs分别表示障碍物和S格中点与横坐标距离值。根据期望横摆角加速度模型：

式中：LS为避障过程中S格的运动距离；lC为自车纵向尺寸。当避障车辆车头与障碍物最近侧纵向距离为L时开始跟踪规划的避障路径，且L＞0。令（x（t），y（t））表示车辆避障轨迹质心的坐标，则避障轨迹为

其中 ta≤t≤tl

2.2.2 弯道路况

在弯道上利用极坐标系进行建模。弯道上所创建S格运动状态以绕弯道圆心角速度表示，且等于障碍物绕弯道圆心角速度，同样，W2和Wzs分别表示障碍物和S格中点相对避障车辆沿极径距离值，示意图如图5所示。

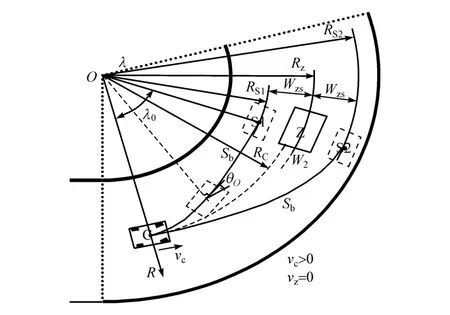
图5 弯道S格创建示意图

图5 中，R为极径，λ为极角，θO为基于动态直角坐标系的横摆角，即自车纵轴与动态直角坐标系横轴的夹角。定义RC，RS和RZ分别为避障车辆、S格和障碍物的极径。图5中以静态障碍物为例，vS／RS＝vZ／RZ＝0。SbR为避障轨迹Sb在极轴上的投影长度，Sbλ表示避障轨迹Sb的极角范围。满足关系式：

针对避障轨迹Sb的规划如下：对于自车θO（t）同样采用正反梯形约束的横摆角加速度模型，轨迹规划的时间段为［ta，tl］，与直道时区别在于式（4）中Sbλ由 SbR表示，满足关系式：

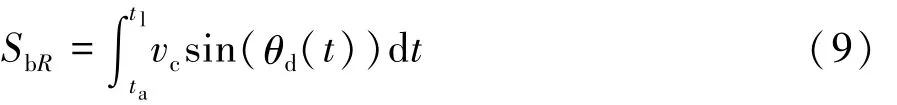
同理，在直道避障过程中纵向距离满足的关系式（6）在弯道极坐标系中表示为

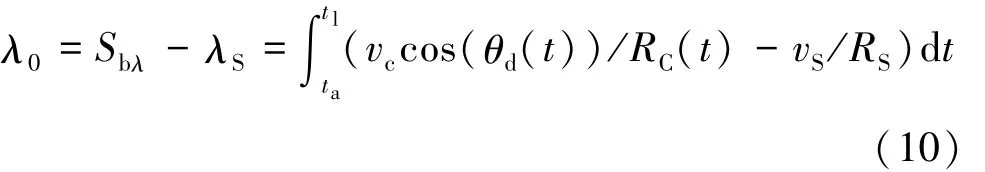
式中λS为［ta，tl］时间内状态格运动的极角范围。令（RC（t），λC（t））表示自车在避障过程中质心的实时极坐标，RC（ta）表示起始阶段自车的极径大小，则避障轨迹为

2.3 多障碍物避障轨迹规划

当出现较多S格时，每相邻两S格之间轨迹规划满足上一节单障碍物避障轨迹规划的策略。出现较多S格时涉及到较优轨迹的求解，提出S格成本的概念，可理解为针对此规划路径进行路径跟踪时的难易程度；同时参考Dijkstra算法进行最优路径选择。关于多障碍物轨迹规划的流程图如图6所示。

图6 流程图

2.3.1 确定可行S格

根据S格的概念制定针对自车位置时所选S格是否可行的判断规则如下。

（1）由图7自车C与目标S格位置创建图中阴影区域，若该区域检测到障碍物，则判断此时S格不可行。

图7 判断规则

（2）已知C车与目标S格的横纵距离后，根据式（6）判断是否满足避障要求的最短纵向距离。

（3）当C车位于某S格位置后，保持直行若无碰撞障碍物的风险，即称此S格为终点S格，视为避障结束。

2.3.2 S格成本计算

对于多条可行S格路径即涉及到最优选择问题，针对所创建S格的状态信息构造计算公式，表示S格路径跟踪的难易程度，即计算S格成本数值越低，该路径越优。根据式（2）～式（4）可知避障轨迹由障碍物状态决定的因素为vs和W。取Wmas和vsmax为轨迹规划中能接受的极值。令σw＝W／Wmax，σvs＝vs／vsmax，同时定义符号ξ为C车到某一S格的成本值，其计算公式为

式中 ξw和 ξvs为权重系数。当

2.3.3 最优路径搜索算法

对于确定的可行S格路径，以C车避障起始点作为根节点，同一障碍物衍生的状态格属于兄弟节点，终点S格称为终节点。借鉴Dijkstra算法得出一条从根节点到终节点的最优路径，此算法中的权值即为S格成本，定义 q（C，S i）为C到 S i格的权值，q（C，S i，S j）＝q（C，S i）+q（S i，S j）。以搭建的搜索树模型为基础，以图8场景为例，具体执行步骤如表1所示（简化说明，不包括障碍物Z4）。

表1 算法执行步骤

最终输出C车从起始位置到任一节点权值最小的路径，再从C车到终节点的路径中选出权值最小的路径做为最终结果。

3 算法的仿真试验

为验证本文中基于衍生状态格的智能车避障轨迹规划算法在路径规划应用中的有效性，通过模拟障碍物环境，运用该算法完成路径规划。

3.1 直道避障仿真试验

为说明基于S格的避障轨迹规划算法应用的可行性，联合 CarSim和 Matlab／Simulink进行仿真试验。为验证算法对速度的鲁棒性，仿真时无人驾驶汽车分别以中速20和高速30 m／s行驶。障碍物场景及所创建对应S格如图8所示，其中vz1＝10 m／s，vz2＝5 m／s，vz3＝7 m／s，vz4＝8 m／s。

图8 创建S格

取 Wmax＝11 m，vsmax＝30 m／s，ξw＝0.3，ξvs＝0.2；通过2.3.3最优路径搜索算法得相应可行S格路径的权值计算结果，如表2所示。

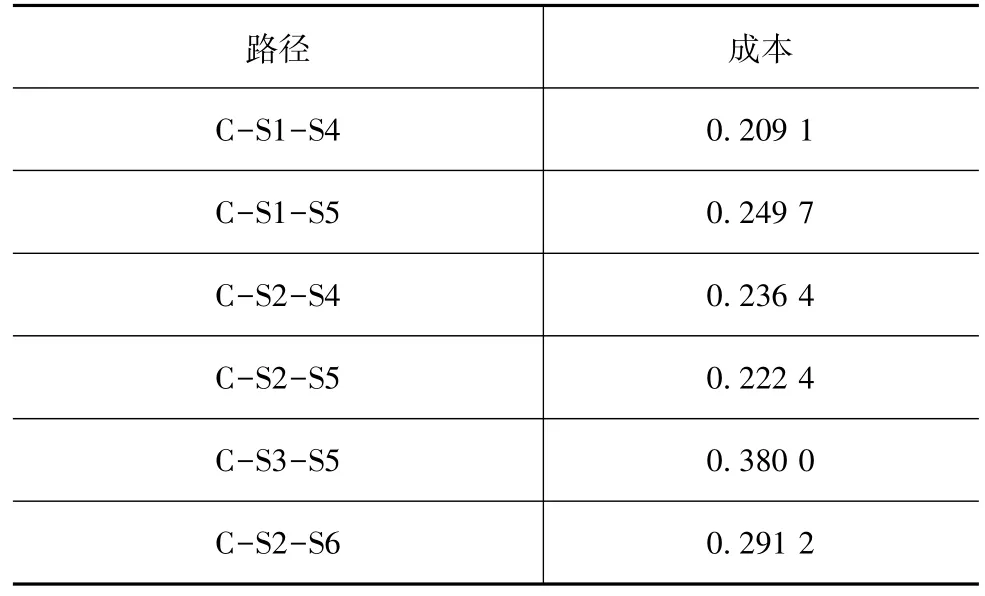
表2 权值计算结果

得最优轨迹为C-S1-S4。若汽车车速为20 m／s，解得 L1＝32 m，L2＝37 m，规划的路径如图9所示。

若汽车以30 m／s的速度恒速行驶时，根据判断规则得出唯一可行轨迹为C-S2-S5。根据策略解得L1＝48.6 m，L2＝62 m，规划的路径如图10所示。

图9 轨迹规划图

图10 轨迹规划图

为进一步研究汽车在跟随路径过程中的运动学特性，基于CarSim平台搭建了环境模型，并将所规划的路径数据用CarSim的动力学模型进行仿真。图11（a）为汽车在此车速下避障时的期望轨迹和跟踪轨迹。图11（b）和图11（c）分别为汽车运动过程中的侧向加速度和横摆角速度的变化情况。由图可见，在动态避障过程中汽车侧向加速度的峰值均低于 0.25 m／s2，横摆角速度峰值均低于 0.15 rad／s。在此路况下，本算法所规划出的轨迹能够满足汽车稳定行驶。

3.2 弯道避障仿真试验

为体现本文避障策略在弯道路况时的有效性，进行弯道避障仿真试验。仿真时所取弯道障碍物场景如图 12所示。其中 vc＝5 m／s，vz＝vs＝0。

确定W1尺寸后创建对应S格，如图12所示。其中以S1格为目标，SbR＝3.5 m。采用 MATLAB／Simulink进行仿真，根据2.2弯道单障碍物避障策略，求得λ0＝55°，并得到规划的避障轨迹，仿真结果如图13所示。

图13（a）为自车极径RC在避障时的仿真曲线，图13（b）为弯道车辆避障过程中期望轨迹，满足行驶过程中曲率连续变化的要求。

3.3 算法的仿真对比试验

图11 汽车动力学特性

栅格法是利用尺寸相同的栅格对二维工作空间进行划分，栅格的大小以自车的尺寸为准。针对动态障碍物，有学者提出时间栅格法［19］。利用本文中建立的模拟场景（图8），运用栅格法完成避障轨迹规划，并与S格法进行对比分析。建立的二维时间栅格环境模型见图14，利用Dijkstra算法对时间栅格进行搜索。软件平台是 MATLAB R2014，得到的两种算法的规划路径对比见图15。

图12 路况图

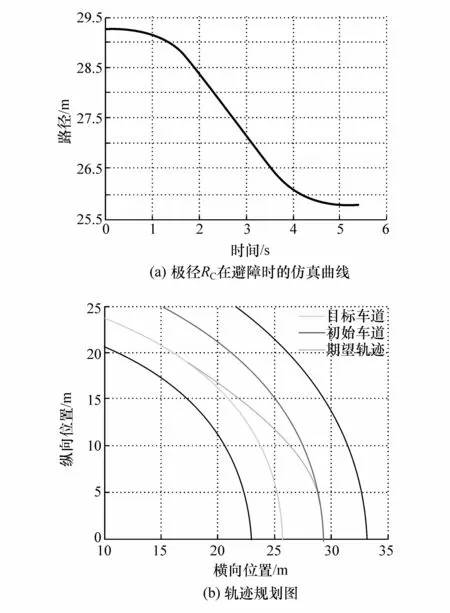
图13 弯道避障仿真结果

图14 时间栅格环境模型

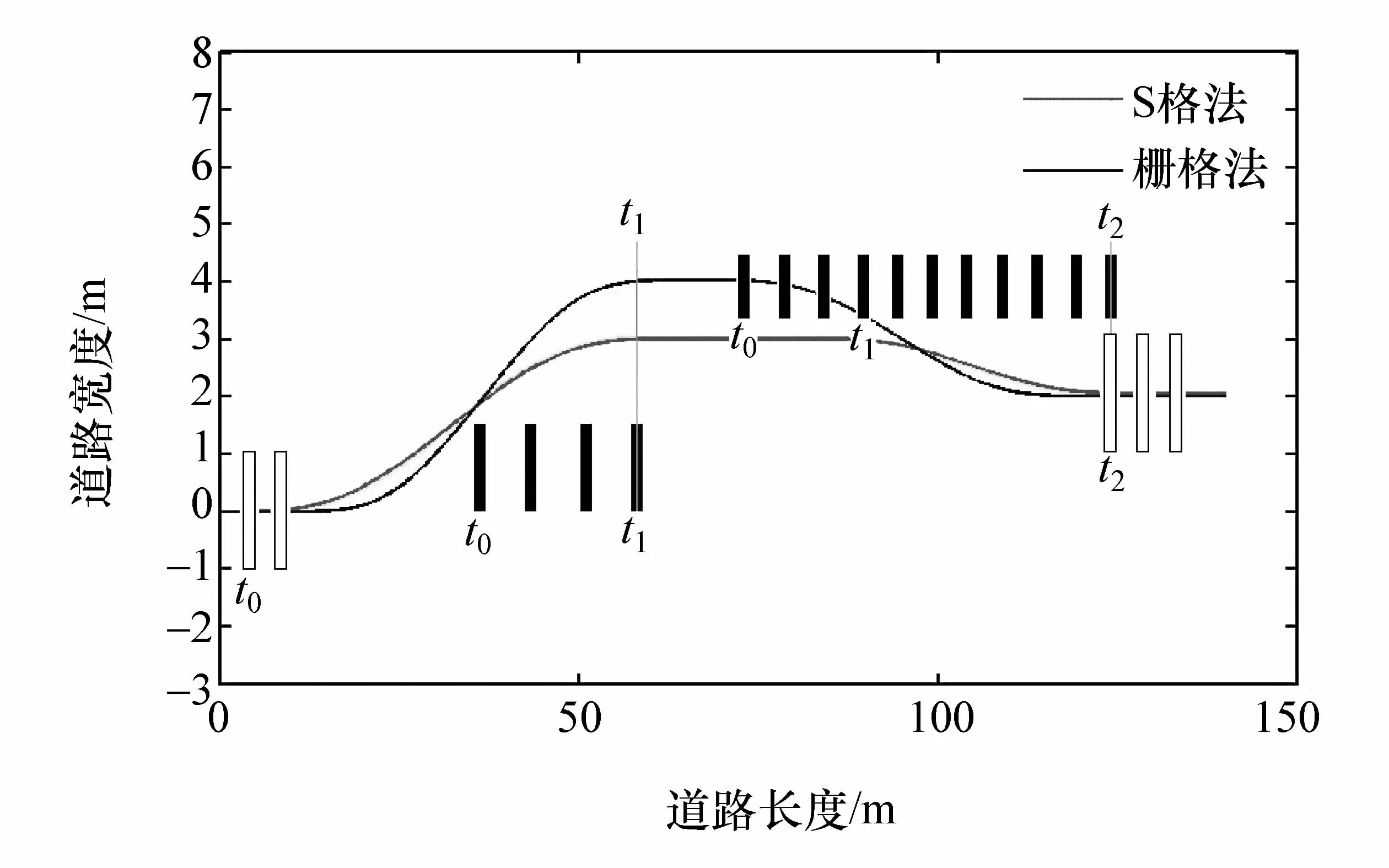
图15 规划路径仿真对比

由图15可见，从所规划轨迹长度和曲率方面来看，利用本文算法所规划的轨迹更优。因为栅格法在规划下一个目的地时，是在已经建立的栅格体系中寻找路径较短的无障碍格。而本文算法以障碍物为出发点建立的S格能很好地控制与障碍物间的距离。图16反映了两种策略分别在搜寻目标栅格和创建S格的区别。

图16 两种策略的对比

图16 中灰色阴影表示目标栅格或者S格。其中（1）和（3）表示同一栅格体系下具有相同目标栅格时障碍物的两种可能位置，（2）和（4）分别表示与（1）和（3）障碍物位置相同时所创建S格的位置。由图可见，本文算法能控制目标S格和障碍物的距离，而栅格法则只能保证目标栅格和障碍物之间的距离在一定的范围内，可能导致避障过程中横向运动较长，轨迹曲率较大。从而进一步说明图15中的仿真结论。

4 硬件在环试验

对本文避障轨迹规划仿真结果通过硬件在环仿真试验进行验证，进一步说明所提出的轨迹规划策略的可行性。装备框图如图17所示。

图17 硬件在环装备框图

该试验台主要由6部分组成，分别是上位机、下位机、接口系统、转向器、控制器和用于模拟转向阻力的伺服电机系统。通过上位机在CarSim中建立整车动力学模型，在Labview中输入规划的避障轨迹，通过CarSim／LabVIEW RT联合，编写轨迹跟踪控制程序，并把命令发送给下位机。下位机为NI的PXI系统，实时运行上位机所建立的仿真程序。接口系统负责将传感器采集到的前轮转角信号输入到PXI实时系统，同时将控制信号输出给执行机构的控制器。

以3.1设定路况场景为例，车速为20和30 m／s时的避障轨迹如图9和图10所示，其硬件在环试验结果如图18所示，起始加入30 m直行距离。

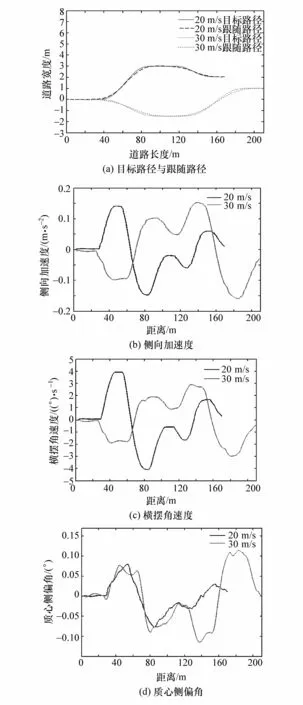
图18 硬件在环试验结果

由图18可见，实际运行轨迹相比规划的目标轨迹存在误差和时滞，这是因为真实转向系统存在载荷且电动机响应相对滞后。对试验所得侧向加速度、横摆加速度和质心侧偏角的峰值进行审核，确定未超过阈值，符合仿真时变化规律，从而保证所规划轨迹能满足车身稳定性。

5 结论

（1）提出衍生状态格的概念，将特定环境下抽象的寻求一条合适的避障轨迹问题转化为具体的根据设定规则的有限解择优问题，在转化过程中全面考虑自车与障碍物的尺寸和运动状态，保证避障轨迹的有效性。

（2）采用正反梯形约束的横摆角加速度模型求出针对S格的换道轨迹，提出S格成本的概念，利用Dijkstra算法对多个可行S格轨迹进行择优。该策略全面考虑单障碍物和多障碍物场景的避障条件，并且在逐渐复杂的环境中避障策略循序渐进。

（3）将本文算法用于避障路径规划中，在特定路况场景两种车速下分别进行了仿真和硬件在环试验。结果表明：汽车按照规划出的路径行驶能够实现安全避障，并且在运动过程中其侧向加速度和横摆角速度值均符合稳定性要求，验证了算法的正确性和有效性。与栅格法进行对比，栅格法需要对整个路况环境搭建栅格再根据障碍物位置进行筛选，而本文算法直接根据障碍物状态创建S格，通过仿真试验证明本文算法所规划的轨迹更短，曲率更小。

（4）本文中主要通过障碍物的状态创建S格，没有考虑车道线、指示牌等标识，也没有考虑各类交通规则，在后期的智能车避障研究中可考虑车道上的各个因素从而创建不仅有针对性还有全面性的S格。